// Databricks notebook source exported at Tue, 28 Jun 2016 11:21:05 UTC
Scalable Data Science
Movie Recommender
Scalable data science project by Harry Wallace
Most of the content below is from Module 5 of Anthony Joseph’s edX course CS100-1x from the Community Edition of databricks that has been added to this databricks shard at /#workspace/scalable-data-science/xtraResources/edXBigDataSeries2015/CS100-1x as extra resources for the project-focussed course Scalable Data Science. Here we use scala instead of python.
(done with significant assistance from Raazesh Sainudiin to write all the code in scala here)
The html source url of this databricks notebook and its recorded Uji  :
:
What is Collaborarive Filtering?
SOURCE: Module 5 of AJ’s course.
Collaborative Filtering
(watch now 61 seconds):
Let us use MLlib to make personalized movie recommendations.
We are going to use a technique called collaborative filtering. Collaborative filtering is a method of making automatic predictions (filtering) about the interests of a user by collecting preferences or taste information from many users (collaborating). The underlying assumption of the collaborative filtering approach is that if a person A has the same opinion as a person B on an issue, A is more likely to have B’s opinion on a different issue x than to have the opinion on x of a person chosen randomly. You can read more about collaborative filtering here.
The image below (from Wikipedia) shows an example of predicting of the user’s rating using collaborative filtering. At first, people rate different items (like videos, images, games). After that, the system is making predictions about a user’s rating for an item, which the user has not rated yet. These predictions are built upon the existing ratings of other users, who have similar ratings with the active user. For instance, in the image below the system has made a prediction, that the active user will not like the video.

Resources:
For movie recommendations, we start with a matrix whose entries are movie ratings by users (shown in red in the diagram below). Each column represents a user (shown in green) and each row represents a particular movie (shown in blue).
Since not all users have rated all movies, we do not know all of the entries in this matrix, which is precisely why we need collaborative filtering. For each user, we have ratings for only a subset of the movies. With collaborative filtering, the idea is to approximate the ratings matrix by factorizing it as the product of two matrices: one that describes properties of each user (shown in green), and one that describes properties of each movie (shown in blue).
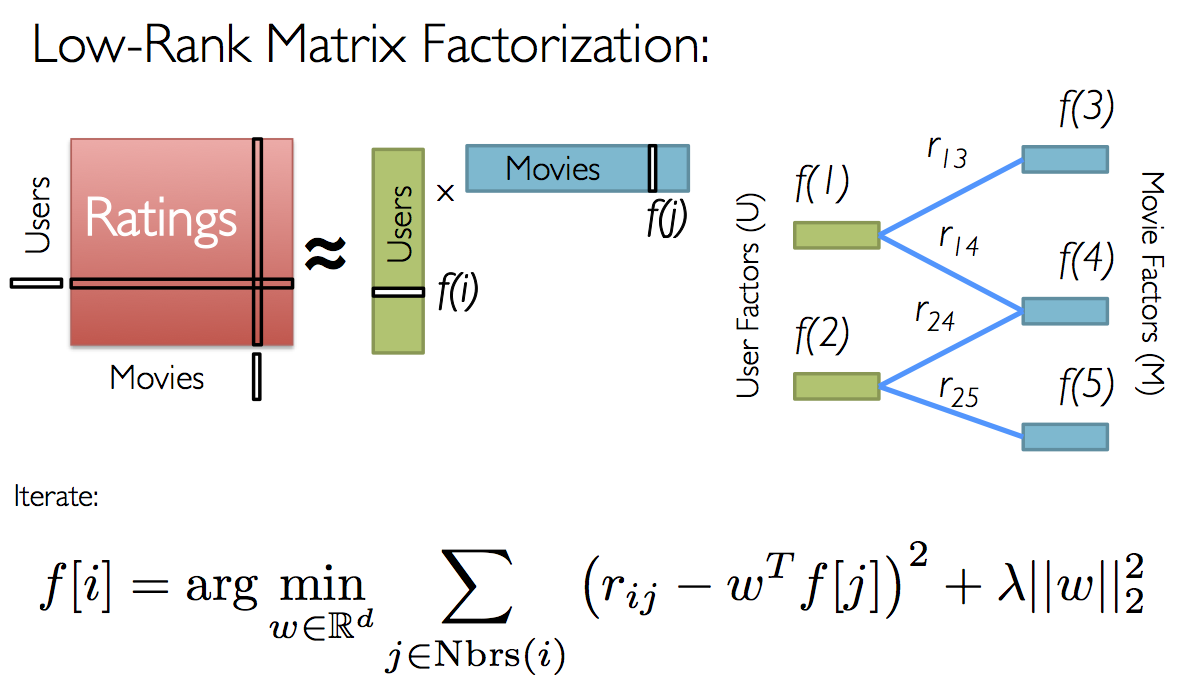
We want to select these two matrices such that the error for the users/movie pairs where we know the correct ratings is minimized. The [Alternating Least Squares][als] algorithm does this by first randomly filling the users matrix with values and then optimizing the value of the movies such that the error is minimized. Then, it holds the movies matrix constrant and optimizes the value of the user’s matrix. This alternation between which matrix to optimize is the reason for the “alternating” in the name.
This optimization is what’s being shown on the right in the image above. Given a fixed set of user factors (i.e., values in the users matrix), we use the known ratings to find the best values for the movie factors using the optimization written at the bottom of the figure. Then we “alternate” and pick the best user factors given fixed movie factors.
For a simple example of what the users and movies matrices might look like, check out the [videos from Lecture 8][videos] or the [slides from Lecture 8][slides] [videos]: https://courses.edx.org/courses/BerkeleyX/CS100.1x/1T2015/courseware/00eb8b17939b4889a41a6d8d2f35db83/3bd3bba368be4102b40780550d3d8da6/ [slides]: https://courses.edx.org/c4x/BerkeleyX/CS100.1x/asset/Week4Lec8.pdf [als]: https://en.wikiversity.org/wiki/Least-Squares_Method
See http://spark.apache.org/docs/latest/mllib-collaborative-filtering.html#collaborative-filtering.
display(dbutils.fs.ls("/databricks-datasets/cs100/lab4/data-001/")) // The data is already here
Import
Let us import the relevant libraries for mllib.
import org.apache.spark.mllib.recommendation.ALS
import org.apache.spark.mllib.recommendation.MatrixFactorizationModel
import org.apache.spark.mllib.recommendation.Rating
Preliminaries
We read in each of the files and create an RDD consisting of parsed lines.
Each line in the ratings dataset (ratings.dat.gz) is formatted as:
UserID::MovieID::Rating::Timestamp
Each line in the movies (movies.dat) dataset is formatted as:
MovieID::Title::Genres
The Genres field has the format
Genres1|Genres2|Genres3|...
The format of these files is uniform and simple, so we can use split().
Parsing the two files yields two RDDS
- For each line in the ratings dataset, we create a tuple of (UserID, MovieID, Rating). We drop the timestamp because we do not need it for this exercise.
- For each line in the movies dataset, we create a tuple of (MovieID, Title). We drop the Genres because we do not need them for this exercise.
val timedRatingsRDD = sc.textFile("/databricks-datasets/cs100/lab4/data-001/ratings.dat.gz").map { line =>
val fields = line.split("::")
// format: (timestamp % 10, Rating(userId, movieId, rating))
(fields(3).toLong % 10, Rating(fields(0).toInt, fields(1).toInt, fields(2).toDouble))
}
We have a look at the first 10 entries in the Ratings RDD to check it’s ok
timedRatingsRDD.take(10).map(println)
The timestamp is unused here so we want to remove it
val ratingsRDD = sc.textFile("/databricks-datasets/cs100/lab4/data-001/ratings.dat.gz").map { line =>
val fields = line.split("::")
// format: Rating(userId, movieId, rating)
Rating(fields(0).toInt, fields(1).toInt, fields(2).toDouble)
}
Now our final ratings RDD looks as follows:
ratingsRDD.take(10).map(println)
A similar command is used to format the movies. We ignore the genres in this recommender
val movies = sc.textFile("/databricks-datasets/cs100/lab4/data-001/movies.dat").map { line =>
val fields = line.split("::")
// format: (movieId, movieName)
(fields(0).toInt, fields(1))
}.collect.toMap
Let’s make a data frame to visually explore the data next.
val timedRatingsDF = sc.textFile("/databricks-datasets/cs100/lab4/data-001/ratings.dat.gz").map { line =>
val fields = line.split("::")
// format: (timestamp % 10, Rating(userId, movieId, rating))
(fields(3).toLong % 10, fields(0).toInt, fields(1).toInt, fields(2).toDouble)
}.toDF("timestamp", "userId", "movieId", "rating")
display(timedRatingsDF)
Here we simply check the size of the datasets we are using
val numRatings = ratingsRDD.count
val numUsers = ratingsRDD.map(_.user).distinct.count
val numMovies = ratingsRDD.map(_.product).distinct.count
println("Got " + numRatings + " ratings from "
+ numUsers + " users on " + numMovies + " movies.")
Now that we have the dataset we need, let’s make a recommender system.
Creating a Training Set, test Set and Validation Set
Before we jump into using machine learning, we need to break up the ratingsRDD dataset into three pieces:
- A training set (RDD), which we will use to train models
- A validation set (RDD), which we will use to choose the best model
- A test set (RDD), which we will use for our experiments
To randomly split the dataset into the multiple groups, we can use the
randomSplit()transformation.randomSplit()takes a set of splits and seed and returns multiple RDDs.
val Array(trainingRDD, validationRDD, testRDD) = ratingsRDD.randomSplit(Array(0.60, 0.20, 0.20), 0L)
After splitting the dataset, your training set has about 293,000 entries and the validation and test sets each have about 97,000 entries (the exact number of entries in each dataset varies slightly due to the random nature of the randomSplit() transformation.
// let's find the exact sizes we have next
println(" training data size = " + trainingRDD.count() +
", validation data size = " + validationRDD.count() +
", test data size = " + testRDD.count() + ".")
See http://spark.apache.org/docs/latest/api/scala/index.html#org.apache.spark.mllib.recommendation.ALS.
(2c) Using ALS.train()
In this part, we will use the MLlib implementation of Alternating Least Squares, ALS.train(). ALS takes a training dataset (RDD) and several parameters that control the model creation process. To determine the best values for the parameters, we will use ALS to train several models, and then we will select the best model and use the parameters from that model in the rest of this lab exercise.
The process we will use for determining the best model is as follows:
- Pick a set of model parameters. The most important parameter to
ALS.train()is the rank, which is the number of rows in the Users matrix (green in the diagram above) or the number of columns in the Movies matrix (blue in the diagram above). (In general, a lower rank will mean higher error on the training dataset, but a high rank may lead to overfitting.) We will train models with ranks of 4, 8, and 12 using thetrainingRDDdataset. - Create a model using
ALS.train(trainingRDD, rank, seed=seed, iterations=iterations, lambda_=regularizationParameter)with three parameters: an RDD consisting of tuples of the form (UserID, MovieID, rating) used to train the model, an integer rank (4, 8, or 12), a number of iterations to execute (we will use 5 for theiterationsparameter), and a regularization coefficient (we will use 0.1 for theregularizationParameter). - For the prediction step, create an input RDD,
validationForPredictRDD, consisting of (UserID, MovieID) pairs that you extract fromvalidationRDD. You will end up with an RDD of the form:[(1, 1287), (1, 594), (1, 1270)] - Using the model and
validationForPredictRDD, we can predict rating values by calling model.predictAll() with thevalidationForPredictRDDdataset, wheremodelis the model we generated with ALS.train().predictAllaccepts an RDD with each entry in the format (userID, movieID) and outputs an RDD with each entry in the format (userID, movieID, rating).
// Build the recommendation model using ALS by fitting to the training data
// using a fixed rank=10, numIterations=10 and regularisation=0.01
val rank = 10
val numIterations = 10
val model = ALS.train(trainingRDD, rank, numIterations, 0.01)
// Evaluate the model on test data
val usersProductsTest = testRDD.map { case Rating(user, product, rate) =>
(user, product)
}
usersProductsTest.take(10) // Checking
// get the predictions on test data
val predictions =
model.predict(usersProductsTest).map { case Rating(user, product, rate) =>
((user, product), rate)
}
// find the actual ratings and join with predictions
val ratesAndPreds = testRDD.map { case Rating(user, product, rate) =>
((user, product), rate)
}.join(predictions)
ratesAndPreds.take(10).map(println) // print first 10 pairs of (user,product) and (true_rating, predicted_rating)
Let’s evaluate the model using Mean Squared Error metric.
val MSE = ratesAndPreds.map { case ((user, product), (r1, r2)) =>
val err = (r1 - r2)
err * err
}.mean()
println("Mean Squared Error = " + MSE)
Can we improve the MSE by changing one of the hyper parameters?
// Build the recommendation model using ALS by fitting to the validation data
// just trying three different hyper-parameter (rank) values to optimise over
val ranks = List(4, 8, 12);
var rank=0;
for ( rank <- ranks ){
val numIterations = 10
val regularizationParameter = 0.01
val model = ALS.train(trainingRDD, rank, numIterations, regularizationParameter)
// Evaluate the model on test data
val usersProductsValidate = validationRDD.map { case Rating(user, product, rate) =>
(user, product)
}
// get the predictions on test data
val predictions = model.predict(usersProductsValidate)
.map { case Rating(user, product, rate)
=> ((user, product), rate)
}
// find the actual ratings and join with predictions
val ratesAndPreds = validationRDD.map { case Rating(user, product, rate)
=> ((user, product), rate)
}.join(predictions)
val MSE = ratesAndPreds.map { case ((user, product), (r1, r2)) =>
val err = (r1 - r2)
err * err
}.mean()
println("rank and Mean Squared Error = " + rank + " and " + MSE)
} // end of loop over ranks
Now let us try to apply this to the test data and find the MSE for the best model.
val rank = 4
val numIterations = 10
val regularizationParameter = 0.01
val model = ALS.train(trainingRDD, rank, numIterations, regularizationParameter)
// Evaluate the model on test data
val usersProductsTest = testRDD.map { case Rating(user, product, rate) =>
(user, product)
}
// get the predictions on test data
val predictions = model.predict(usersProductsTest)
.map { case Rating(user, product, rate)
=> ((user, product), rate)
}
// find the actual ratings and join with predictions
val ratesAndPreds = testRDD.map { case Rating(user, product, rate)
=> ((user, product), rate)
}.join(predictions)
val MSE = ratesAndPreds.map { case ((user, product), (r1, r2)) =>
val err = (r1 - r2)
err * err
}.mean()
println("rank and Mean Squared Error for test data = " + rank + " and " + MSE)
** Potential flaws of CF **
- Cold start for users and items
- Synonym faults
- Grey/Black sheep, individuality
- Shilling
- Positive feedback problems (rich-get-richer effect)
** Areas to improve upon **
- Works in theory but didn’t manage to produce a system that takes user info and outputs suggestions
- More complete models would include analysing the genres to give better recommendations.
- For first time users, the program could give the top rated movies over all users.
- Could have used bigger dataset
End of Presentation
An Example for working with dataset that is downloaded from the internet…
The following is adapted from http://spark.apache.org/docs/latest/mllib-collaborative-filtering.html#collaborative-filtering.
See supplementary notebook ‘loadMoviesData’ for instructions on downloading the data on movie ratings and loading into dbfs.
In the following example we load rating data. Each row consists of a user, a product and a rating. We use the default ALS.train() method which assumes ratings are explicit. We evaluate the recommendation model by measuring the Mean Squared Error of rating prediction.
import org.apache.spark.mllib.recommendation.ALS
import org.apache.spark.mllib.recommendation.MatrixFactorizationModel
import org.apache.spark.mllib.recommendation.Rating
// Load the data
val ratingsText = sc.textFile("dbfs:/datasets/movies/ml-latest-small/ratings.csv")
val ratingsTextLarge = sc.textFile("dbfs:/datasets/movies/ml-10M100K/ratings.dat")
val moviesTextSmall = sc.textFile("dbfs:/datasets/movies/ml-latest-small/movies.csv")
val moviesTextLarge = sc.textFile("dbfs:/datasets/movies/ml-10M100K/movies.dat")
moviesTextLarge.take(10).map(println) // see first 10 lines
Let’s obtain a dataframe from this structured CSV file to quickly emplore the data.
val ratingsDF = sqlContext.read
.format("com.databricks.spark.csv") // use spark.csv package
.option("header", "true") // Use first line of all files as header
.option("inferSchema", "true") // Automatically infer data types
.option("delimiter", ",") // Specify the delimiter as comma or ',' DEFAULT
.load("dbfs:/datasets/movies/ml-latest-small/ratings.csv")
ratingsDF.take(10)
display(ratingsDF) // play with the GUI plots to explore further...
For using mllib we need to get an RDD made of rows of org.apache.spark.mllib.recommendation.Rating as follows:
val ratings = ratingsText
.mapPartitionsWithIndex { (idx, iter) => if (idx == 0) iter.drop(1) else iter } // to drop first line
.map(_.split(',') match { case Array(user, item, rate, timestamp) =>
Rating(user.toInt, item.toInt, rate.toDouble) // to get Rating from user, item, rate
})
// Build the recommendation model using ALS
val rank = 10
val numIterations = 10
val model = ALS.train(ratings, rank, numIterations, 0.01)
// Evaluate the model on rating data
val usersProducts = ratings.map { case Rating(user, product, rate) =>
(user, product)
}
val predictions =
model.predict(usersProducts).map { case Rating(user, product, rate) =>
((user, product), rate)
}
val ratesAndPreds = ratings.map { case Rating(user, product, rate) =>
((user, product), rate)
}.join(predictions)
val MSE = ratesAndPreds.map { case ((user, product), (r1, r2)) =>
val err = (r1 - r2)
err * err
}.mean()
println("Mean Squared Error = " + MSE)
What does ALS.trainImplicit do?
Explain this by looking at the docs…
val alpha = 0.01
val lambda = 0.01
val model = ALS.trainImplicit(ratings, rank, numIterations, lambda, alpha)
// Save and load model - SKIP for now
//model.save(sc, "target/tmp/myCollaborativeFilter") // "target/tmp/myCollaborativeFilter" should be appropriately chosen
//val sameModel = MatrixFactorizationModel.load(sc, "target/tmp/myCollaborativeFilter")
Scalable Data Science
Movie Recommender
Scalable data science project by Harry Wallace
Most of the content below is from Module 5 of Anthony Joseph’s edX course CS100-1x from the Community Edition of databricks that has been added to this databricks shard at /#workspace/scalable-data-science/xtraResources/edXBigDataSeries2015/CS100-1x as extra resources for the project-focussed course Scalable Data Science. Here we use scala instead of python.
(done with significant assistance from Raazesh Sainudiin for all the code in scala here)



