// Databricks notebook source exported at Sun, 19 Jun 2016 08:59:36 UTC
Scalable Data Science
prepared by Raazesh Sainudiin and Sivanand Sivaram
The html source url of this databricks notebook and its recorded Uji  :
:
Linear Algebra Review / re-Introduction
by Ameet Talwalkar in BerkeleyX: CS190.1x Scalable Machine Learning
This is a breeze‘y scalarific break-down of:
- Ameet’s Linear Algebra Review in CS190.1x Scalable Machine Learning Course that is archived in edX from 2015 and
- Home Work: read this! https://github.com/scalanlp/breeze/wiki/Quickstart
Using the above resources we’ll provide a review of basic linear algebra concepts that will recur throughout the course. These concepts include:
- Matrices
- Vectors
- Arithmetic operations with vectors and matrices
We will see the accompanying Scala computations in the local or non-distributed setting.
Let’s get a quick visual geometric interpretation for vectors, matrices and matrix-vector multiplications from the first interactive visual-cognitive aid at:
- http://setosa.io/ev/eigenvectors-and-eigenvalues/ just focus on geometric interpretation of vectors and matrices in Cartesian coordinates.
Matrix by Ameet Talwalkar in BerkeleyX: CS190.1x Scalable Machine Learning
(watch now 0:50):
Breeze is a linear algebra package in Scala. First, let us import it as follows:
import breeze.linalg._
1. Matrix: creation and element-access
A matrix is a two-dimensional array.
Let us denote matrices via bold uppercase letters as follows:
For instance, the matrix below is denoted with \(\mathbf{A}\), a capital bold A.
\[\mathbf{A} = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\]We usually put commas between the row and column indexing sub-scripts, to make the possibly multi-digit indices distinguishable as follows:
\[\mathbf{A} = \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \end{pmatrix}\]- \(\mathbf{A}_{i,j}\) denotes the entry in \(i\)-th row and \(j\)-th column of the matrix \(\mathbf{A}\).
- So for instance,
- the first entry, the top left entry, is denoted by \(\mathbf{A}_{1,1}\).
- And the entry in the third row and second column is denoted by \(\mathbf{A}_{3,2}\).
- We say that a matrix with n rows and m columns is an \(n\) by \(m\) matrix and written as \(n \times m\)
- The matrix \(\mathbf{A}\) shown above is a generic \(3 \times 3\) (pronounced 3-by-3) matrix.
- And the matrix in Ameet’s example in the video above, having 4 rows and 3 columns, is a 4 by 3 matrix.
- If a matrix \(\mathbf{A}\) is \(n \times m\), we write:
- \(\mathbf{A} \in \mathbb{R}^{n \times m}\) and say that \(\mathbf{A}\) is an \(\mathbb{R}\) to the power of the n times m,
- where, \(\mathbb{R}\) here denotes the set of all real numbers in the line given by the open interval: \((-\infty,+\infty)\).
- \(\mathbf{A} \in \mathbb{R}^{n \times m}\) and say that \(\mathbf{A}\) is an \(\mathbb{R}\) to the power of the n times m,
Let us created a matrix A as a val (that is immutable) in scala. The matrix we want to create is mathematically notated as follows:
\(\mathbf{A} = \begin{pmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\
a_{2,1} & a_{2,2} & a_{2,3}
\end{pmatrix}
=
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6
\end{pmatrix}\)
val A = DenseMatrix((1, 2, 3), (4, 5, 6)) // let's create this 2 by 3 matrix
A.size
A.rows // number of rows
A.size / A.rows // num of columns
Now, let’s access the element \(a_{1,1}\), i.e., the element from the first row and first column of \(\mathbf{A}\), which in our val A matrix is the integer of type Int equalling 1.
A(0, 0) // Remember elements are indexed by zero in scala
Gotcha: indices in breeze matrices start at 0 as in numpy of python and not at 1 as in MATLAB!
Of course if you assign the same dense matrix to a mutable var B then its entries can be modified as follows:
var B = DenseMatrix((1, 2, 3), (4, 5, 6))
B(0,0)=999; B(1,1)=969; B(0,2)=666
B
Vector
(watch now 0:31):
- A vector is a matrix with many rows and one column.
-
We’ll denote a vector by bold lowercase letters: \(\mathbf{a} = \begin{pmatrix} 3.3 \\ 1.0 \\ 6.3 \\ 3.6 \end{pmatrix}\)
So, the vector above is denoted by \(\mathbf{a}\), the lowercase, bold a.
- \(a_i\) denotes the i-th entry of a vector. So for instance:
- \(a_2\) denotes the second entry of the vector and it is 1.0 for our vector.
- If a vector is m-dimensional, then we say that \(\mathbf{a}\) is in \(\mathbb{R}^m\) and write \(\mathbf{a} \in \mathbb{R}^m\).
- So our \(\mathbf{a} \in \mathbb{R}^4\).
val a = DenseVector(3.3, 1.0, 6.3, 3.6) // these are row vectors
a.size // a is a column vector of size 4
a(1) // the second element of a is indexed by 1 as the first element is indexed by 0
val a = DenseVector[Double](5, 4, -1) // this makes a vector of Doubles from input Int
val a = DenseVector(5.0, 4.0, -1.0) // this makes a vector of Doubles from type inference . NOTE "5.0" is needed not jsy "5."
val x = DenseVector.zeros[Double](5) // this will output x: breeze.linalg.DenseVector[Double] = DenseVector(0.0, 0.0, 0.0, 0.0, 0.0)
Transpose
(watch now 1:02):
Suggested Home Work for the linear-algebraically rusty (LiAlRusty): watch again and take notes.
val A = DenseMatrix((1, 4), (6, 1), (3, 5)) // let's create this 2 by 3 matrix
A.t // transpose of A
val a = DenseVector(3.0, 4.0, 1.0)
a.t
Addition and Subtraction
(watch now 0:59):
Suggested Home Work for LiAlRusty: watch again and take notes.
Pop Quiz:
- what is a natural geometric interpretation of vector addition, subtraction, matric addition and subtraction?
val A = DenseMatrix((1, 4), (6, 1), (3, 5))
val B = -A
A + B // should be A-A=0
A - B // should be A+A=2A
B - A // should be -A-A=-2A
Operators
All Tensors support a set of operators, similar to those used in Matlab or Numpy.
For HOMEWORK see: Workspace -> scalable-data-science -> xtraResources -> LinearAlgebra -> LAlgCheatSheet for a list of most of the operators and various operations.
Some of the basic ones are reproduced here, to give you an idea.
| Operation | Breeze | Matlab | Numpy |
|---|---|---|---|
| Elementwise addition | a + b |
a + b |
a + b |
| Elementwise multiplication | a :* b |
a .* b |
a * b |
| Elementwise comparison | a :< b |
a < b (gives matrix of 1/0 instead of true/false) |
a < b |
| Inplace addition | a :+= 1.0 |
a += 1 |
a += 1 |
| Inplace elementwise multiplication | a :*= 2.0 |
a *= 2 |
a *= 2 |
| Vector dot product | a dot b,a.t * b† |
dot(a,b) |
dot(a,b) |
| Elementwise sum | sum(a) |
sum(sum(a)) |
a.sum() |
| Elementwise max | a.max |
max(a) |
a.max() |
| Elementwise argmax | argmax(a) |
argmax(a) |
a.argmax() |
| Ceiling | ceil(a) |
ceil(a) |
ceil(a) |
| Floor | floor(a) |
floor(a) |
floor(a) |
Scalar multiplication, Dot Product and Matrix-Vector multiplication
(watch now 2:26):
Suggested Home Work for LiAlRusty: watch again and take notes.
Pop Quiz:
- what is a natural geometric interpretation of scalar multiplication of a vector or a matrix and what about vector matrix multiplication?
Let’s get a quick visual geometric interpretation for vectors, matrices and matrix-vector multiplications from the first interactive visual-cognitive aid at:
val A = DenseMatrix((1, 4), (6, 1), (3, 5))
5 * A
A * 5
Dot product
val A = DenseMatrix((1, 4), (6, 1), (3, 5))
val B = DenseMatrix((3, 1), (2, 2), (1, 3))
A :* B // element-wise multiplication
Matrix Vector multiplication
val A = DenseMatrix((1, 4), (3, 1))
val a = DenseVector(1, -1) // is a column vector
a.size // a is a column vector of size 2
A * a
Matrix-Matrix multiplication
(watch now 1:59):
val A = DenseMatrix((1,2,3),(1,1,1))
val B = DenseMatrix((4, 1), (9, 2), (8, 9))
A*B // 4+18+14
1*4 + 2*9 + 3*8 // checking first entry of A*B
Identity Matrix
(watch now 0:53):
val A = DenseMatrix((1,2,3),(4,5,6))
A * DenseMatrix.eye[Int](3)
DenseMatrix.eye[Int](2) * A
Inverse
(watch now 0:52):
val D = DenseMatrix((2.0, 3.0), (4.0, 5.0))
val Dinv = inv(D)
D * Dinv
Dinv * D
Eucledian distance / norm
(watch now 0:52):
val b = DenseVector(4, 3)
norm(b)
Math.sqrt(4*4 + 3*3) // check
HOMEWORK: read this! https://github.com/scalanlp/breeze/wiki/Quickstart
It is here in markdown’d via wget and pandoc for your convenience.
Scala / nlp / breeze / Quickstart
David Hall edited this page on 24 Dec 2015
Breeze is modeled on Scala, and so if you’re familiar with it, you’ll be familiar with Breeze. First, import the linear algebra package:
scala> import breeze.linalg._
Let’s create a vector:
scala> val x = DenseVector.zeros[Double](5)
x: breeze.linalg.DenseVector[Double] = DenseVector(0.0, 0.0, 0.0, 0.0, 0.0)
Here we make a column vector of zeros of type Double. And there are other ways we could create the vector - such as with a literal DenseVector(1,2,3) or with a call to fill or tabulate. The vector is “dense” because it is backed by an Array[Double], but could as well have created a SparseVector.zeros[Double](5), which would not allocate memory for zeros.
Unlike Scalala, all Vectors are column vectors. Row vectors are represented as Transpose[Vector[T]].
The vector object supports accessing and updating data elements by their index in 0 to x.length-1. Like Numpy, negative indices are supported, with the semantics that for an index i < 0 we operate on the i-th element from the end (x(i) == x(x.length + i)).
scala> x(0)
Double = 0.0
scala> x(1) = 2
scala> x
breeze.linalg.DenseVector[Double] = DenseVector(0.0, 2.0, 0.0, 0.0, 0.0)
Breeze also supports slicing. Note that slices using a Range are much, much faster than those with an arbitrary sequence.
scala> x(3 to 4) := .5
breeze.linalg.DenseVector[Double] = DenseVector(0.5, 0.5)
scala> x
breeze.linalg.DenseVector[Double] = DenseVector(0.0, 2.0, 0.0, 0.5, 0.5)
The slice operator constructs a read-through and write-through view of the given elements in the underlying vector. You set its values using the vectorized-set operator :=. You could as well have set it to a compatibly sized Vector.
scala> x(0 to 1) := DenseVector(.1,.2)
scala> x
breeze.linalg.DenseVector[Double] = DenseVector(0.1, 0.2, 0.0, 0.5, 0.5)
Similarly, a DenseMatrix can be created with a constructor method call, and its elements can be accessed and updated.
scala> val m = DenseMatrix.zeros[Int](5,5)
m: breeze.linalg.DenseMatrix[Int] =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
The columns of m can be accessed as DenseVectors, and the rows as DenseMatrices.
scala> (m.rows, m.cols)
(Int, Int) = (5,5)
scala> m(::,1)
breeze.linalg.DenseVector[Int] = DenseVector(0, 0, 0, 0, 0)
scala> m(4,::) := DenseVector(1,2,3,4,5).t // transpose to match row shape
breeze.linalg.DenseMatrix[Int] = 1 2 3 4 5
scala> m
breeze.linalg.DenseMatrix[Int] =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
1 2 3 4 5
Assignments with incompatible cardinality or a larger numeric type won’t compile.
scala> m := x
<console>:13: error: could not find implicit value for parameter op: breeze.linalg.operators.BinaryUpdateOp[breeze.linalg.DenseMatrix[Int],breeze.linalg.DenseVector[Double],breeze.linalg.operators.OpSet]
m := x
^
Assignments with incompatible size will throw an exception:
scala> m := DenseMatrix.zeros[Int](3,3)
java.lang.IllegalArgumentException: requirement failed: Matrices must have same number of row
Sub-matrices can be sliced and updated, and literal matrices can be specified using a simple tuple-based syntax. Unlike Scalala, only range slices are supported, and only the columns (or rows for a transposed matrix) can have a Range step size different from 1.
scala> m(0 to 1, 0 to 1) := DenseMatrix((3,1),(-1,-2))
breeze.linalg.DenseMatrix[Int] =
3 1
-1 -2
scala> m
breeze.linalg.DenseMatrix[Int] =
3 1 0 0 0
-1 -2 0 0 0
0 0 0 0 0
0 0 0 0 0
1 2 3 4 5
Broadcasting
Sometimes we want to apply an operation to every row or column of a matrix, as a unit. For instance, you might want to compute the mean of each row, or add a vector to every column. Adapting a matrix so that operations can be applied column-wise or row-wise is called broadcasting. Languages like R and numpy automatically and implicitly do broadcasting, meaning they won’t stop you if you accidentally add a matrix and a vector. In Breeze, you have to signal your intent using the broadcasting operator *. The * is meant to evoke “foreach” visually. Here are some examples:
scala> import breeze.stats.mean
scala> val dm = DenseMatrix((1.0,2.0,3.0),
(4.0,5.0,6.0))
scala> val res = dm(::, *) + DenseVector(3.0, 4.0)
breeze.linalg.DenseMatrix[Double] =
4.0 5.0 6.0
8.0 9.0 10.0
scala> res(::, *) := DenseVector(3.0, 4.0)
scala> res
breeze.linalg.DenseMatrix[Double] =
3.0 3.0 3.0
4.0 4.0 4.0
scala> mean(dm(*, ::))
breeze.linalg.DenseVector[Double] = DenseVector(2.0, 5.0)
breeze.stats.distributions
Breeze also provides a fairly large number of probability distributions. These come with access to probability density function for either discrete or continuous distributions. Many distributions also have methods for giving the mean and the variance.
scala> import breeze.stats.distributions._
scala> val poi = new Poisson(3.0);
poi: breeze.stats.distributions.Poisson = <function1>
scala> val s = poi.sample(5);
s: IndexedSeq[Int] = Vector(5, 4, 5, 7, 4)
scala> s map { poi.probabilityOf(_) }
IndexedSeq[Double] = Vector(0.10081881344492458, 0.16803135574154085, 0.10081881344492458, 0.02160403145248382, 0.16803135574154085)
scala> val doublePoi = for(x <- poi) yield x.toDouble // meanAndVariance requires doubles, but Poisson samples over Ints
doublePoi: breeze.stats.distributions.Rand[Double] = breeze.stats.distributions.Rand$$anon$11@1b52e04
scala> breeze.stats.meanAndVariance(doublePoi.samples.take(1000));
breeze.stats.MeanAndVariance = MeanAndVariance(2.9960000000000067,2.9669509509509533,1000)
scala> (poi.mean,poi.variance)
(Double, Double) = (3.0,3.0)
NOTE: Below, there is a possibility of confusion for the term rate in the family of exponential distributions. Breeze parameterizes the distribution with the mean, but refers to it as the rate.
scala> val expo = new Exponential(0.5);
expo: breeze.stats.distributions.Exponential = Exponential(0.5)
scala> expo.rate
Double = 0.5
A characteristic of exponential distributions is its half-life, but we can compute the probability a value falls between any two numbers.
scala> expo.probability(0, log(2) * expo.rate)
Double = 0.5
scala> expo.probability(0.0, 1.5)
Double = 0.950212931632136
This means that approximately 95% of the draws from an exponential distribution fall between 0 and thrice the mean. We could have easily computed this with the cumulative distribution as well
scala> 1 - exp(-3.0)
Double = 0.950212931632136
scala> val samples = expo.sample(2).sorted;
samples: IndexedSeq[Double] = Vector(1.1891135726280517, 2.325607782657507)
scala> expo.probability(samples(0), samples(1));
Double = 0.08316481553047272
scala> breeze.stats.meanAndVariance(expo.samples.take(10000));
breeze.stats.MeanAndVariance = MeanAndVariance(2.029351863973081,4.163267835527843,10000)
scala> (1 / expo.rate, 1 / (expo.rate * expo.rate))
(Double, Double) = (2.0,4.0)
breeze.optimize
TODO: document breeze.optimize.minimize, recommend that instead.
Breeze’s optimization package includes several convex optimization routines and a simple linear program solver. Convex optimization routines typically take a
DiffFunction[T], which is a Function1 extended to have a gradientAt method, which returns the gradient at a particular point. Most routines will require
a breeze.linalg-enabled type: something like a Vector or a Counter.
Here’s a simple DiffFunction: a parabola along each vector’s coordinate.
scala> import breeze.optimize._
scala> val f = new DiffFunction[DenseVector[Double]] {
| def calculate(x: DenseVector[Double]) = {
| (norm((x - 3d) :^ 2d,1d),(x * 2d) - 6d);
| }
| }
f: java.lang.Object with breeze.optimize.DiffFunction[breeze.linalg.DenseVector[Double]] = $anon$1@617746b2
Note that this function takes its minimum when all values are 3. (It’s just a parabola along each coordinate.)
scala> f.valueAt(DenseVector(3,3,3))
Double = 0.0
scala> f.gradientAt(DenseVector(3,0,1))
breeze.linalg.DenseVector[Double] = DenseVector(0.0, -6.0, -4.0)
scala> f.calculate(DenseVector(0,0))
(Double, breeze.linalg.DenseVector[Double]) = (18.0,DenseVector(-6.0, -6.0))
You can also use approximate derivatives, if your function is easy enough to compute:
scala> def g(x: DenseVector[Double]) = (x - 3.0):^ 2.0 sum
scala> g(DenseVector(0.,0.,0.))
Double = 27.0
scala> val diffg = new ApproximateGradientFunction(g)
scala> diffg.gradientAt(DenseVector(3,0,1))
breeze.linalg.DenseVector[Double] = DenseVector(1.000000082740371E-5, -5.999990000127297, -3.999990000025377)
Ok, now let’s optimize f. The easiest routine to use is just LBFGS, which is a quasi-Newton method that works well for most problems.
scala> val lbfgs = new LBFGS[DenseVector[Double]](maxIter=100, m=3) // m is the memory. anywhere between 3 and 7 is fine. The larger m, the more memory is needed.
scala> val optimum = lbfgs.minimize(f,DenseVector(0,0,0))
optimum: breeze.linalg.DenseVector[Double] = DenseVector(2.9999999999999973, 2.9999999999999973, 2.9999999999999973)
scala> f(optimum)
Double = 2.129924444096732E-29
That’s pretty close to 0! You can also use a configurable optimizer, using FirstOrderMinimizer.OptParams. It takes several parameters:
case class OptParams(batchSize:Int = 512,
regularization: Double = 1.0,
alpha: Double = 0.5,
maxIterations:Int = -1,
useL1: Boolean = false,
tolerance:Double = 1E-4,
useStochastic: Boolean= false) {
// ...
}
batchSize applies to BatchDiffFunctions, which support using small minibatches of a dataset. regularization integrates L2 or L1 (depending on useL1) regularization with constant lambda. alpha controls the initial stepsize for algorithms that need it. maxIterations is the maximum number of gradient steps to be taken (or -1 for until convergence). tolerance controls the sensitivity of the
convergence check. Finally, useStochastic determines whether or not batch functions should be optimized using a stochastic gradient algorithm (using small batches), or using LBFGS (using the entire dataset).
OptParams can be controlled using breeze.config.Configuration, which we described earlier.
breeze.optimize.linear
We provide a DSL for solving linear programs, using Apache’s Simplex Solver as the backend. This package isn’t industrial strength yet by any means, but it’s good for simple problems. The DSL is pretty simple:
import breeze.optimize.linear._
val lp = new LinearProgram()
import lp._
val x0 = Real()
val x1 = Real()
val x2 = Real()
val lpp = ( (x0 + x1 * 2 + x2 * 3 )
subjectTo ( x0 * -1 + x1 + x2 <= 20)
subjectTo ( x0 - x1 * 3 + x2 <= 30)
subjectTo ( x0 <= 40 )
)
val result = maximize( lpp)
assert( norm(result.result - DenseVector(40.0,17.5,42.5), 2) < 1E-4)
We also have specialized routines for bipartite matching (KuhnMunkres and CompetitiveLinking) and flow problems.
Breeze-Viz
**This API is highly experimental. It may change greatly. **
Breeze continues most of the functionality of Scalala’s plotting facilities, though the API is somewhat different (in particular, more object oriented.) These methods are documented in scaladoc for the traits in the breeze.plot package object. First, let’s plot some lines and save the image to file. All the actual plotting work is done by the excellent JFreeChart library.
import breeze.linalg._
import breeze.plot._
val f = Figure()
val p = f.subplot(0)
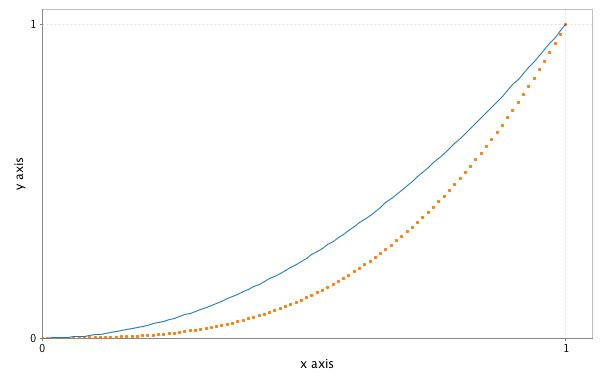
val x = linspace(0.0,1.0)
p += plot(x, x :^ 2.0)
p += plot(x, x :^ 3.0, '.')
p.xlabel = "x axis"
p.ylabel = "y axis"
f.saveas("lines.png") // save current figure as a .png, eps and pdf also supported
Then we’ll add a new subplot and plot a histogram of 100,000 normally distributed random numbers into 100 buckets.
val p2 = f.subplot(2,1,1)
val g = breeze.stats.distributions.Gaussian(0,1)
p2 += hist(g.sample(100000),100)
p2.title = "A normal distribution"
f.saveas("subplots.png")

Breeze also supports the Matlab-like “image” command, here imaging a random matrix.
val f2 = Figure()
f2.subplot(0) += image(DenseMatrix.rand(200,200))
f2.saveas("image.png")

Where to go next?
After reading this quickstart, you can go to other wiki pages, especially Linear Algebra Cheat-Sheet and Data Structures.
Big O Notation for Space and Time Complexity by Ameet Talwalkar in BerkeleyX: CS190.1x Scalable Machine Learning
(watch later 5:52):
Watch this and take notes!




