ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Please feel free to refer to basic concepts here:
- Udacity's course on Deep Learning https://www.udacity.com/course/deep-learning--ud730 by Google engineers: Arpan Chakraborty and Vincent Vanhoucke and their full video playlist:
Entering the 4th Dimension
Networks for Understanding Time-Oriented Patterns in Data
Common time-based problems include * Sequence modeling: "What comes next?" * Likely next letter, word, phrase, category, cound, action, value * Sequence-to-Sequence modeling: "What alternative sequence is a pattern match?" (i.e., similar probability distribution) * Machine translation, text-to-speech/speech-to-text, connected handwriting (specific scripts)

Simplified Approaches
- If we know all of the sequence states and the probabilities of state transition...
- ... then we have a simple Markov Chain model.
- If we don't know all of the states or probabilities (yet) but can make constraining assumptions and acquire solid information from observing (sampling) them...
- ... we can use a Hidden Markov Model approach.
These approached have only limited capacity because they are effectively stateless and so have some degree of "extreme retrograde amnesia."
Can we use a neural network to learn the "next" record in a sequence?
First approach, using what we already know, might look like * Clamp input sequence to a vector of neurons in a feed-forward network * Learn a model on the class of the next input record
Let's try it! This can work in some situations, although it's more of a setup and starting point for our next development.
We will make up a simple example of the English alphabet sequence wehere we try to predict the next alphabet from a sequence of length 3.
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print (seq_in, '->', seq_out)
ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z
# dataX is just a reindexing of the alphabets in consecutive triplets of numbers
dataX
dataY # just a reindexing of the following alphabet after each consecutive triplet of numbers
Train a network on that data:
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM # <- this is the Long-Short-term memory layer
from keras.utils import np_utils
# begin data generation ------------------------------------------
# this is just a repeat of what we did above
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print (seq_in, '->', seq_out)
# end data generation ---------------------------------------------
X = numpy.reshape(dataX, (len(dataX), seq_length))
X = X / float(len(alphabet)) # normalize the mapping of alphabets from integers into [0, 1]
y = np_utils.to_categorical(dataY) # make the output we want to predict to be categorical
# keras architecturing of a feed forward dense or fully connected Neural Network
model = Sequential()
# draw the architecture of the network given by next two lines, hint: X.shape[1] = 3, y.shape[1] = 26
model.add(Dense(30, input_dim=X.shape[1], kernel_initializer='normal', activation='relu'))
model.add(Dense(y.shape[1], activation='softmax'))
# keras compiling and fitting
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=1000, batch_size=5, verbose=2)
scores = model.evaluate(X, y)
print("Model Accuracy: %.2f " % scores[1])
for pattern in dataX:
x = numpy.reshape(pattern, (1, len(pattern)))
x = x / float(len(alphabet))
prediction = model.predict(x, verbose=0) # get prediction from fitted model
index = numpy.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
print (seq_in, "->", result) # print the predicted outputs
Using TensorFlow backend.
ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Epoch 1/1000
- 1s - loss: 3.2612 - acc: 0.0435
Epoch 2/1000
- 0s - loss: 3.2585 - acc: 0.0435
Epoch 3/1000
- 0s - loss: 3.2564 - acc: 0.0435
Epoch 4/1000
- 0s - loss: 3.2543 - acc: 0.0435
Epoch 5/1000
- 0s - loss: 3.2529 - acc: 0.0435
Epoch 6/1000
- 0s - loss: 3.2507 - acc: 0.0435
Epoch 7/1000
- 0s - loss: 3.2491 - acc: 0.0435
Epoch 8/1000
- 0s - loss: 3.2473 - acc: 0.0435
Epoch 9/1000
- 0s - loss: 3.2455 - acc: 0.0435
Epoch 10/1000
- 0s - loss: 3.2438 - acc: 0.0435
Epoch 11/1000
- 0s - loss: 3.2415 - acc: 0.0435
Epoch 12/1000
- 0s - loss: 3.2398 - acc: 0.0435
Epoch 13/1000
- 0s - loss: 3.2378 - acc: 0.0435
Epoch 14/1000
- 0s - loss: 3.2354 - acc: 0.0435
Epoch 15/1000
- 0s - loss: 3.2336 - acc: 0.0435
Epoch 16/1000
- 0s - loss: 3.2313 - acc: 0.0435
Epoch 17/1000
- 0s - loss: 3.2293 - acc: 0.0435
Epoch 18/1000
- 0s - loss: 3.2268 - acc: 0.0435
Epoch 19/1000
- 0s - loss: 3.2248 - acc: 0.0435
Epoch 20/1000
- 0s - loss: 3.2220 - acc: 0.0435
Epoch 21/1000
- 0s - loss: 3.2196 - acc: 0.0435
Epoch 22/1000
- 0s - loss: 3.2168 - acc: 0.0435
Epoch 23/1000
- 0s - loss: 3.2137 - acc: 0.0435
Epoch 24/1000
- 0s - loss: 3.2111 - acc: 0.0435
Epoch 25/1000
- 0s - loss: 3.2082 - acc: 0.0435
Epoch 26/1000
- 0s - loss: 3.2047 - acc: 0.0435
Epoch 27/1000
- 0s - loss: 3.2018 - acc: 0.0435
Epoch 28/1000
- 0s - loss: 3.1984 - acc: 0.0435
Epoch 29/1000
- 0s - loss: 3.1950 - acc: 0.0435
Epoch 30/1000
- 0s - loss: 3.1918 - acc: 0.0435
Epoch 31/1000
- 0s - loss: 3.1883 - acc: 0.0435
Epoch 32/1000
- 0s - loss: 3.1849 - acc: 0.0435
Epoch 33/1000
- 0s - loss: 3.1808 - acc: 0.0435
Epoch 34/1000
- 0s - loss: 3.1776 - acc: 0.0435
Epoch 35/1000
- 0s - loss: 3.1736 - acc: 0.0435
Epoch 36/1000
- 0s - loss: 3.1700 - acc: 0.0435
Epoch 37/1000
- 0s - loss: 3.1655 - acc: 0.0435
Epoch 38/1000
- 0s - loss: 3.1618 - acc: 0.0870
Epoch 39/1000
- 0s - loss: 3.1580 - acc: 0.0435
Epoch 40/1000
- 0s - loss: 3.1533 - acc: 0.0870
Epoch 41/1000
- 0s - loss: 3.1487 - acc: 0.0870
Epoch 42/1000
- 0s - loss: 3.1447 - acc: 0.0870
Epoch 43/1000
- 0s - loss: 3.1408 - acc: 0.0870
Epoch 44/1000
- 0s - loss: 3.1361 - acc: 0.0870
Epoch 45/1000
- 0s - loss: 3.1317 - acc: 0.0870
Epoch 46/1000
- 0s - loss: 3.1275 - acc: 0.0870
Epoch 47/1000
- 0s - loss: 3.1233 - acc: 0.0870
Epoch 48/1000
- 0s - loss: 3.1188 - acc: 0.0870
Epoch 49/1000
- 0s - loss: 3.1142 - acc: 0.0870
Epoch 50/1000
- 0s - loss: 3.1099 - acc: 0.0870
Epoch 51/1000
- 0s - loss: 3.1051 - acc: 0.0870
Epoch 52/1000
- 0s - loss: 3.1007 - acc: 0.0870
Epoch 53/1000
- 0s - loss: 3.0963 - acc: 0.0870
Epoch 54/1000
- 0s - loss: 3.0913 - acc: 0.0870
Epoch 55/1000
- 0s - loss: 3.0875 - acc: 0.0870
Epoch 56/1000
- 0s - loss: 3.0825 - acc: 0.0870
Epoch 57/1000
- 0s - loss: 3.0783 - acc: 0.0870
Epoch 58/1000
- 0s - loss: 3.0732 - acc: 0.0870
Epoch 59/1000
- 0s - loss: 3.0685 - acc: 0.0870
Epoch 60/1000
- 0s - loss: 3.0644 - acc: 0.0870
Epoch 61/1000
- 0s - loss: 3.0596 - acc: 0.0870
Epoch 62/1000
- 0s - loss: 3.0550 - acc: 0.1304
Epoch 63/1000
- 0s - loss: 3.0505 - acc: 0.0870
Epoch 64/1000
- 0s - loss: 3.0458 - acc: 0.0870
Epoch 65/1000
- 0s - loss: 3.0419 - acc: 0.0870
Epoch 66/1000
- 0s - loss: 3.0368 - acc: 0.0870
Epoch 67/1000
- 0s - loss: 3.0327 - acc: 0.0870
Epoch 68/1000
- 0s - loss: 3.0282 - acc: 0.0870
Epoch 69/1000
- 0s - loss: 3.0232 - acc: 0.0870
Epoch 70/1000
- 0s - loss: 3.0189 - acc: 0.0870
Epoch 71/1000
- 0s - loss: 3.0139 - acc: 0.0870
Epoch 72/1000
- 0s - loss: 3.0093 - acc: 0.0870
Epoch 73/1000
- 0s - loss: 3.0049 - acc: 0.0870
Epoch 74/1000
- 0s - loss: 3.0006 - acc: 0.0870
Epoch 75/1000
- 0s - loss: 2.9953 - acc: 0.0870
Epoch 76/1000
- 0s - loss: 2.9910 - acc: 0.0870
Epoch 77/1000
- 0s - loss: 2.9868 - acc: 0.0870
Epoch 78/1000
- 0s - loss: 2.9826 - acc: 0.0870
Epoch 79/1000
- 0s - loss: 2.9773 - acc: 0.0870
Epoch 80/1000
- 0s - loss: 2.9728 - acc: 0.0870
Epoch 81/1000
- 0s - loss: 2.9683 - acc: 0.0870
Epoch 82/1000
- 0s - loss: 2.9640 - acc: 0.0870
Epoch 83/1000
- 0s - loss: 2.9594 - acc: 0.0870
Epoch 84/1000
- 0s - loss: 2.9550 - acc: 0.0870
Epoch 85/1000
- 0s - loss: 2.9508 - acc: 0.0870
Epoch 86/1000
- 0s - loss: 2.9461 - acc: 0.0870
Epoch 87/1000
- 0s - loss: 2.9415 - acc: 0.0870
Epoch 88/1000
- 0s - loss: 2.9372 - acc: 0.0870
Epoch 89/1000
- 0s - loss: 2.9331 - acc: 0.1304
Epoch 90/1000
- 0s - loss: 2.9284 - acc: 0.1304
Epoch 91/1000
- 0s - loss: 2.9239 - acc: 0.1304
Epoch 92/1000
- 0s - loss: 2.9192 - acc: 0.1304
Epoch 93/1000
- 0s - loss: 2.9148 - acc: 0.1304
Epoch 94/1000
- 0s - loss: 2.9105 - acc: 0.1304
Epoch 95/1000
- 0s - loss: 2.9061 - acc: 0.1304
Epoch 96/1000
- 0s - loss: 2.9018 - acc: 0.1304
Epoch 97/1000
- 0s - loss: 2.8975 - acc: 0.1304
Epoch 98/1000
- 0s - loss: 2.8932 - acc: 0.1304
Epoch 99/1000
- 0s - loss: 2.8889 - acc: 0.1304
Epoch 100/1000
- 0s - loss: 2.8844 - acc: 0.1304
Epoch 101/1000
- 0s - loss: 2.8803 - acc: 0.1304
Epoch 102/1000
- 0s - loss: 2.8758 - acc: 0.1304
Epoch 103/1000
- 0s - loss: 2.8717 - acc: 0.1304
Epoch 104/1000
- 0s - loss: 2.8674 - acc: 0.0870
Epoch 105/1000
- 0s - loss: 2.8634 - acc: 0.0870
Epoch 106/1000
- 0s - loss: 2.8586 - acc: 0.0870
Epoch 107/1000
- 0s - loss: 2.8547 - acc: 0.0870
Epoch 108/1000
- 0s - loss: 2.8505 - acc: 0.0870
Epoch 109/1000
- 0s - loss: 2.8462 - acc: 0.0870
Epoch 110/1000
- 0s - loss: 2.8421 - acc: 0.0870
Epoch 111/1000
- 0s - loss: 2.8383 - acc: 0.0870
Epoch 112/1000
- 0s - loss: 2.8337 - acc: 0.0870
Epoch 113/1000
- 0s - loss: 2.8299 - acc: 0.0870
Epoch 114/1000
- 0s - loss: 2.8257 - acc: 0.0870
Epoch 115/1000
- 0s - loss: 2.8216 - acc: 0.0870
Epoch 116/1000
- 0s - loss: 2.8173 - acc: 0.0870
Epoch 117/1000
- 0s - loss: 2.8134 - acc: 0.0870
Epoch 118/1000
- 0s - loss: 2.8094 - acc: 0.0870
Epoch 119/1000
- 0s - loss: 2.8058 - acc: 0.0870
Epoch 120/1000
- 0s - loss: 2.8016 - acc: 0.0870
Epoch 121/1000
- 0s - loss: 2.7975 - acc: 0.1304
Epoch 122/1000
- 0s - loss: 2.7934 - acc: 0.1304
Epoch 123/1000
- 0s - loss: 2.7895 - acc: 0.1304
Epoch 124/1000
- 0s - loss: 2.7858 - acc: 0.1304
Epoch 125/1000
- 0s - loss: 2.7820 - acc: 0.1304
Epoch 126/1000
- 0s - loss: 2.7782 - acc: 0.1304
Epoch 127/1000
- 0s - loss: 2.7738 - acc: 0.1304
Epoch 128/1000
- 0s - loss: 2.7696 - acc: 0.1304
Epoch 129/1000
- 0s - loss: 2.7661 - acc: 0.1304
Epoch 130/1000
- 0s - loss: 2.7625 - acc: 0.1304
Epoch 131/1000
- 0s - loss: 2.7587 - acc: 0.1304
Epoch 132/1000
- 0s - loss: 2.7547 - acc: 0.1304
Epoch 133/1000
- 0s - loss: 2.7513 - acc: 0.1304
Epoch 134/1000
- 0s - loss: 2.7476 - acc: 0.1304
Epoch 135/1000
- 0s - loss: 2.7436 - acc: 0.1304
Epoch 136/1000
- 0s - loss: 2.7398 - acc: 0.1304
Epoch 137/1000
- 0s - loss: 2.7365 - acc: 0.0870
Epoch 138/1000
- 0s - loss: 2.7326 - acc: 0.0870
Epoch 139/1000
- 0s - loss: 2.7288 - acc: 0.1304
Epoch 140/1000
- 0s - loss: 2.7250 - acc: 0.1304
Epoch 141/1000
- 0s - loss: 2.7215 - acc: 0.1304
Epoch 142/1000
- 0s - loss: 2.7182 - acc: 0.1304
Epoch 143/1000
- 0s - loss: 2.7148 - acc: 0.1304
Epoch 144/1000
- 0s - loss: 2.7112 - acc: 0.1304
Epoch 145/1000
- 0s - loss: 2.7077 - acc: 0.1304
Epoch 146/1000
- 0s - loss: 2.7041 - acc: 0.1304
Epoch 147/1000
- 0s - loss: 2.7010 - acc: 0.1304
Epoch 148/1000
- 0s - loss: 2.6973 - acc: 0.1304
Epoch 149/1000
- 0s - loss: 2.6939 - acc: 0.0870
Epoch 150/1000
- 0s - loss: 2.6910 - acc: 0.0870
Epoch 151/1000
- 0s - loss: 2.6873 - acc: 0.0870
Epoch 152/1000
- 0s - loss: 2.6839 - acc: 0.0870
Epoch 153/1000
- 0s - loss: 2.6805 - acc: 0.1304
Epoch 154/1000
- 0s - loss: 2.6773 - acc: 0.1304
Epoch 155/1000
- 0s - loss: 2.6739 - acc: 0.1304
Epoch 156/1000
- 0s - loss: 2.6707 - acc: 0.1739
Epoch 157/1000
- 0s - loss: 2.6676 - acc: 0.1739
Epoch 158/1000
- 0s - loss: 2.6639 - acc: 0.1739
Epoch 159/1000
- 0s - loss: 2.6608 - acc: 0.1739
Epoch 160/1000
- 0s - loss: 2.6577 - acc: 0.1739
Epoch 161/1000
- 0s - loss: 2.6542 - acc: 0.1739
Epoch 162/1000
- 0s - loss: 2.6513 - acc: 0.1739
Epoch 163/1000
- 0s - loss: 2.6479 - acc: 0.1739
Epoch 164/1000
- 0s - loss: 2.6447 - acc: 0.1739
Epoch 165/1000
- 0s - loss: 2.6420 - acc: 0.1739
Epoch 166/1000
- 0s - loss: 2.6386 - acc: 0.1739
Epoch 167/1000
- 0s - loss: 2.6355 - acc: 0.1739
Epoch 168/1000
- 0s - loss: 2.6327 - acc: 0.1739
Epoch 169/1000
- 0s - loss: 2.6296 - acc: 0.1739
Epoch 170/1000
- 0s - loss: 2.6268 - acc: 0.1739
Epoch 171/1000
- 0s - loss: 2.6235 - acc: 0.1739
Epoch 172/1000
- 0s - loss: 2.6203 - acc: 0.1739
Epoch 173/1000
- 0s - loss: 2.6179 - acc: 0.1739
Epoch 174/1000
- 0s - loss: 2.6147 - acc: 0.1739
Epoch 175/1000
- 0s - loss: 2.6121 - acc: 0.1739
Epoch 176/1000
- 0s - loss: 2.6088 - acc: 0.1739
Epoch 177/1000
- 0s - loss: 2.6058 - acc: 0.1739
Epoch 178/1000
- 0s - loss: 2.6034 - acc: 0.1739
Epoch 179/1000
- 0s - loss: 2.6001 - acc: 0.1739
Epoch 180/1000
- 0s - loss: 2.5969 - acc: 0.1739
Epoch 181/1000
- 0s - loss: 2.5945 - acc: 0.1739
Epoch 182/1000
- 0s - loss: 2.5921 - acc: 0.1739
Epoch 183/1000
- 0s - loss: 2.5886 - acc: 0.1739
Epoch 184/1000
- 0s - loss: 2.5862 - acc: 0.1739
Epoch 185/1000
- 0s - loss: 2.5837 - acc: 0.1304
Epoch 186/1000
- 0s - loss: 2.5805 - acc: 0.1739
Epoch 187/1000
- 0s - loss: 2.5778 - acc: 0.1739
Epoch 188/1000
- 0s - loss: 2.5753 - acc: 0.1739
Epoch 189/1000
- 0s - loss: 2.5727 - acc: 0.1739
Epoch 190/1000
- 0s - loss: 2.5695 - acc: 0.1739
Epoch 191/1000
- 0s - loss: 2.5669 - acc: 0.1739
Epoch 192/1000
- 0s - loss: 2.5643 - acc: 0.1739
Epoch 193/1000
- 0s - loss: 2.5614 - acc: 0.1739
Epoch 194/1000
- 0s - loss: 2.5591 - acc: 0.1739
Epoch 195/1000
- 0s - loss: 2.5566 - acc: 0.1739
Epoch 196/1000
- 0s - loss: 2.5535 - acc: 0.1739
Epoch 197/1000
- 0s - loss: 2.5511 - acc: 0.1739
Epoch 198/1000
- 0s - loss: 2.5484 - acc: 0.1739
Epoch 199/1000
- 0s - loss: 2.5458 - acc: 0.1739
Epoch 200/1000
- 0s - loss: 2.5433 - acc: 0.1739
Epoch 201/1000
- 0s - loss: 2.5411 - acc: 0.1739
Epoch 202/1000
- 0s - loss: 2.5383 - acc: 0.1739
Epoch 203/1000
- 0s - loss: 2.5357 - acc: 0.1739
Epoch 204/1000
- 0s - loss: 2.5328 - acc: 0.1739
Epoch 205/1000
- 0s - loss: 2.5308 - acc: 0.1739
Epoch 206/1000
- 0s - loss: 2.5281 - acc: 0.1739
Epoch 207/1000
- 0s - loss: 2.5261 - acc: 0.1739
Epoch 208/1000
- 0s - loss: 2.5237 - acc: 0.1739
Epoch 209/1000
- 0s - loss: 2.5208 - acc: 0.1739
Epoch 210/1000
- 0s - loss: 2.5189 - acc: 0.1739
Epoch 211/1000
- 0s - loss: 2.5162 - acc: 0.1739
Epoch 212/1000
- 0s - loss: 2.5136 - acc: 0.1739
Epoch 213/1000
- 0s - loss: 2.5111 - acc: 0.1739
Epoch 214/1000
- 0s - loss: 2.5088 - acc: 0.1739
Epoch 215/1000
- 0s - loss: 2.5066 - acc: 0.1739
Epoch 216/1000
- 0s - loss: 2.5041 - acc: 0.1739
Epoch 217/1000
- 0s - loss: 2.5018 - acc: 0.1739
Epoch 218/1000
- 0s - loss: 2.4993 - acc: 0.1739
Epoch 219/1000
- 0s - loss: 2.4968 - acc: 0.1739
Epoch 220/1000
- 0s - loss: 2.4947 - acc: 0.1739
Epoch 221/1000
- 0s - loss: 2.4922 - acc: 0.1739
Epoch 222/1000
- 0s - loss: 2.4898 - acc: 0.1739
Epoch 223/1000
- 0s - loss: 2.4878 - acc: 0.1739
Epoch 224/1000
- 0s - loss: 2.4856 - acc: 0.1739
Epoch 225/1000
- 0s - loss: 2.4833 - acc: 0.1739
Epoch 226/1000
- 0s - loss: 2.4808 - acc: 0.1739
Epoch 227/1000
- 0s - loss: 2.4786 - acc: 0.1739
Epoch 228/1000
- 0s - loss: 2.4763 - acc: 0.1739
Epoch 229/1000
- 0s - loss: 2.4739 - acc: 0.1739
Epoch 230/1000
- 0s - loss: 2.4722 - acc: 0.1739
Epoch 231/1000
- 0s - loss: 2.4699 - acc: 0.1739
Epoch 232/1000
- 0s - loss: 2.4681 - acc: 0.1739
Epoch 233/1000
- 0s - loss: 2.4658 - acc: 0.1739
Epoch 234/1000
- 0s - loss: 2.4633 - acc: 0.1739
Epoch 235/1000
- 0s - loss: 2.4612 - acc: 0.1739
Epoch 236/1000
- 0s - loss: 2.4589 - acc: 0.1739
Epoch 237/1000
- 0s - loss: 2.4569 - acc: 0.1739
Epoch 238/1000
- 0s - loss: 2.4543 - acc: 0.1739
Epoch 239/1000
- 0s - loss: 2.4524 - acc: 0.1739
Epoch 240/1000
- 0s - loss: 2.4505 - acc: 0.1739
Epoch 241/1000
- 0s - loss: 2.4487 - acc: 0.1739
Epoch 242/1000
- 0s - loss: 2.4464 - acc: 0.1739
Epoch 243/1000
- 0s - loss: 2.4440 - acc: 0.1739
Epoch 244/1000
- 0s - loss: 2.4420 - acc: 0.1739
Epoch 245/1000
- 0s - loss: 2.4405 - acc: 0.1739
Epoch 246/1000
- 0s - loss: 2.4380 - acc: 0.2174
Epoch 247/1000
- 0s - loss: 2.4362 - acc: 0.2174
Epoch 248/1000
- 0s - loss: 2.4340 - acc: 0.2174
Epoch 249/1000
- 0s - loss: 2.4324 - acc: 0.2174
Epoch 250/1000
- 0s - loss: 2.4301 - acc: 0.2174
Epoch 251/1000
- 0s - loss: 2.4284 - acc: 0.2174
Epoch 252/1000
- 0s - loss: 2.4260 - acc: 0.2174
Epoch 253/1000
- 0s - loss: 2.4239 - acc: 0.2174
Epoch 254/1000
- 0s - loss: 2.4217 - acc: 0.2174
Epoch 255/1000
- 0s - loss: 2.4200 - acc: 0.2174
Epoch 256/1000
- 0s - loss: 2.4182 - acc: 0.2174
Epoch 257/1000
- 0s - loss: 2.4160 - acc: 0.2174
Epoch 258/1000
- 0s - loss: 2.4142 - acc: 0.2174
Epoch 259/1000
- 0s - loss: 2.4125 - acc: 0.2174
Epoch 260/1000
- 0s - loss: 2.4102 - acc: 0.1739
Epoch 261/1000
- 0s - loss: 2.4084 - acc: 0.1739
Epoch 262/1000
- 0s - loss: 2.4060 - acc: 0.1739
Epoch 263/1000
- 0s - loss: 2.4044 - acc: 0.1739
Epoch 264/1000
- 0s - loss: 2.4028 - acc: 0.2174
Epoch 265/1000
- 0s - loss: 2.4008 - acc: 0.2174
Epoch 266/1000
- 0s - loss: 2.3985 - acc: 0.2174
Epoch 267/1000
- 0s - loss: 2.3964 - acc: 0.2174
Epoch 268/1000
- 0s - loss: 2.3951 - acc: 0.1739
Epoch 269/1000
- 0s - loss: 2.3931 - acc: 0.2174
Epoch 270/1000
- 0s - loss: 2.3910 - acc: 0.2174
Epoch 271/1000
- 0s - loss: 2.3892 - acc: 0.2174
Epoch 272/1000
- 0s - loss: 2.3876 - acc: 0.2174
Epoch 273/1000
- 0s - loss: 2.3856 - acc: 0.2174
Epoch 274/1000
- 0s - loss: 2.3837 - acc: 0.2174
Epoch 275/1000
- 0s - loss: 2.3823 - acc: 0.2174
Epoch 276/1000
- 0s - loss: 2.3807 - acc: 0.2174
Epoch 277/1000
- 0s - loss: 2.3786 - acc: 0.2609
Epoch 278/1000
- 0s - loss: 2.3770 - acc: 0.2609
Epoch 279/1000
- 0s - loss: 2.3749 - acc: 0.2609
Epoch 280/1000
- 0s - loss: 2.3735 - acc: 0.2609
Epoch 281/1000
- 0s - loss: 2.3718 - acc: 0.2609
Epoch 282/1000
- 0s - loss: 2.3697 - acc: 0.2609
Epoch 283/1000
- 0s - loss: 2.3677 - acc: 0.2609
Epoch 284/1000
- 0s - loss: 2.3665 - acc: 0.2174
Epoch 285/1000
- 0s - loss: 2.3643 - acc: 0.2174
Epoch 286/1000
- 0s - loss: 2.3627 - acc: 0.2174
Epoch 287/1000
- 0s - loss: 2.3609 - acc: 0.1739
Epoch 288/1000
- 0s - loss: 2.3592 - acc: 0.1739
Epoch 289/1000
- 0s - loss: 2.3575 - acc: 0.1739
Epoch 290/1000
- 0s - loss: 2.3560 - acc: 0.1739
Epoch 291/1000
- 0s - loss: 2.3540 - acc: 0.1739
Epoch 292/1000
- 0s - loss: 2.3523 - acc: 0.2174
Epoch 293/1000
- 0s - loss: 2.3506 - acc: 0.2174
Epoch 294/1000
- 0s - loss: 2.3486 - acc: 0.2174
Epoch 295/1000
- 0s - loss: 2.3471 - acc: 0.2174
Epoch 296/1000
- 0s - loss: 2.3451 - acc: 0.2609
Epoch 297/1000
- 0s - loss: 2.3438 - acc: 0.2609
Epoch 298/1000
- 0s - loss: 2.3421 - acc: 0.2609
Epoch 299/1000
- 0s - loss: 2.3398 - acc: 0.2609
Epoch 300/1000
- 0s - loss: 2.3389 - acc: 0.2174
Epoch 301/1000
- 0s - loss: 2.3374 - acc: 0.2174
Epoch 302/1000
- 0s - loss: 2.3356 - acc: 0.2174
Epoch 303/1000
- 0s - loss: 2.3336 - acc: 0.2174
Epoch 304/1000
- 0s - loss: 2.3325 - acc: 0.2174
Epoch 305/1000
- 0s - loss: 2.3305 - acc: 0.2609
Epoch 306/1000
- 0s - loss: 2.3290 - acc: 0.2609
Epoch 307/1000
- 0s - loss: 2.3271 - acc: 0.2609
Epoch 308/1000
- 0s - loss: 2.3256 - acc: 0.2609
Epoch 309/1000
- 0s - loss: 2.3240 - acc: 0.2174
Epoch 310/1000
- 0s - loss: 2.3222 - acc: 0.2174
Epoch 311/1000
- 0s - loss: 2.3204 - acc: 0.2609
Epoch 312/1000
- 0s - loss: 2.3190 - acc: 0.2609
Epoch 313/1000
- 0s - loss: 2.3176 - acc: 0.2609
Epoch 314/1000
- 0s - loss: 2.3155 - acc: 0.2609
Epoch 315/1000
- 0s - loss: 2.3141 - acc: 0.2609
Epoch 316/1000
- 0s - loss: 2.3124 - acc: 0.2609
Epoch 317/1000
- 0s - loss: 2.3112 - acc: 0.2609
Epoch 318/1000
- 0s - loss: 2.3095 - acc: 0.2609
Epoch 319/1000
- 0s - loss: 2.3077 - acc: 0.2609
Epoch 320/1000
- 0s - loss: 2.3061 - acc: 0.2609
Epoch 321/1000
- 0s - loss: 2.3048 - acc: 0.2609
Epoch 322/1000
- 0s - loss: 2.3030 - acc: 0.2609
Epoch 323/1000
- 0s - loss: 2.3016 - acc: 0.2609
Epoch 324/1000
- 0s - loss: 2.3000 - acc: 0.2609
Epoch 325/1000
- 0s - loss: 2.2985 - acc: 0.3043
Epoch 326/1000
- 0s - loss: 2.2965 - acc: 0.3043
Epoch 327/1000
- 0s - loss: 2.2953 - acc: 0.3043
Epoch 328/1000
- 0s - loss: 2.2942 - acc: 0.3043
Epoch 329/1000
- 0s - loss: 2.2920 - acc: 0.3043
Epoch 330/1000
- 0s - loss: 2.2911 - acc: 0.3043
Epoch 331/1000
- 0s - loss: 2.2897 - acc: 0.3043
Epoch 332/1000
- 0s - loss: 2.2880 - acc: 0.3478
Epoch 333/1000
- 0s - loss: 2.2864 - acc: 0.3478
Epoch 334/1000
- 0s - loss: 2.2851 - acc: 0.3043
Epoch 335/1000
- 0s - loss: 2.2839 - acc: 0.3043
Epoch 336/1000
- 0s - loss: 2.2823 - acc: 0.3043
Epoch 337/1000
- 0s - loss: 2.2806 - acc: 0.3043
Epoch 338/1000
- 0s - loss: 2.2795 - acc: 0.3043
Epoch 339/1000
- 0s - loss: 2.2782 - acc: 0.3043
Epoch 340/1000
- 0s - loss: 2.2764 - acc: 0.3043
Epoch 341/1000
- 0s - loss: 2.2749 - acc: 0.3043
Epoch 342/1000
- 0s - loss: 2.2737 - acc: 0.3043
Epoch 343/1000
- 0s - loss: 2.2719 - acc: 0.3043
Epoch 344/1000
- 0s - loss: 2.2707 - acc: 0.3043
Epoch 345/1000
- 0s - loss: 2.2693 - acc: 0.3043
Epoch 346/1000
- 0s - loss: 2.2677 - acc: 0.3043
Epoch 347/1000
- 0s - loss: 2.2663 - acc: 0.3043
Epoch 348/1000
- 0s - loss: 2.2648 - acc: 0.3043
Epoch 349/1000
- 0s - loss: 2.2634 - acc: 0.3043
Epoch 350/1000
- 0s - loss: 2.2622 - acc: 0.3043
Epoch 351/1000
- 0s - loss: 2.2605 - acc: 0.3043
Epoch 352/1000
- 0s - loss: 2.2590 - acc: 0.3043
Epoch 353/1000
- 0s - loss: 2.2574 - acc: 0.3043
Epoch 354/1000
- 0s - loss: 2.2558 - acc: 0.2609
Epoch 355/1000
- 0s - loss: 2.2551 - acc: 0.3043
Epoch 356/1000
- 0s - loss: 2.2536 - acc: 0.3043
Epoch 357/1000
- 0s - loss: 2.2519 - acc: 0.2609
Epoch 358/1000
- 0s - loss: 2.2510 - acc: 0.3043
Epoch 359/1000
- 0s - loss: 2.2496 - acc: 0.3478
Epoch 360/1000
- 0s - loss: 2.2484 - acc: 0.3043
Epoch 361/1000
- 0s - loss: 2.2469 - acc: 0.3043
Epoch 362/1000
- 0s - loss: 2.2451 - acc: 0.3043
Epoch 363/1000
- 0s - loss: 2.2441 - acc: 0.3043
Epoch 364/1000
- 0s - loss: 2.2432 - acc: 0.3478
Epoch 365/1000
- 0s - loss: 2.2409 - acc: 0.3478
Epoch 366/1000
- 0s - loss: 2.2398 - acc: 0.3478
Epoch 367/1000
- 0s - loss: 2.2387 - acc: 0.3478
Epoch 368/1000
- 0s - loss: 2.2372 - acc: 0.3478
Epoch 369/1000
- 0s - loss: 2.2360 - acc: 0.3478
Epoch 370/1000
- 0s - loss: 2.2341 - acc: 0.3043
Epoch 371/1000
- 0s - loss: 2.2331 - acc: 0.3043
Epoch 372/1000
- 0s - loss: 2.2317 - acc: 0.3043
Epoch 373/1000
- 0s - loss: 2.2306 - acc: 0.3043
Epoch 374/1000
- 0s - loss: 2.2293 - acc: 0.3043
Epoch 375/1000
- 0s - loss: 2.2276 - acc: 0.3043
Epoch 376/1000
- 0s - loss: 2.2269 - acc: 0.3043
Epoch 377/1000
- 0s - loss: 2.2250 - acc: 0.2609
Epoch 378/1000
- 0s - loss: 2.2243 - acc: 0.2609
Epoch 379/1000
- 0s - loss: 2.2222 - acc: 0.3043
Epoch 380/1000
- 0s - loss: 2.2212 - acc: 0.3043
Epoch 381/1000
- 0s - loss: 2.2201 - acc: 0.3043
Epoch 382/1000
- 0s - loss: 2.2192 - acc: 0.3043
Epoch 383/1000
- 0s - loss: 2.2177 - acc: 0.3043
Epoch 384/1000
- 0s - loss: 2.2157 - acc: 0.3043
Epoch 385/1000
- 0s - loss: 2.2140 - acc: 0.3043
Epoch 386/1000
- 0s - loss: 2.2137 - acc: 0.3043
Epoch 387/1000
- 0s - loss: 2.2126 - acc: 0.3043
Epoch 388/1000
- 0s - loss: 2.2108 - acc: 0.3043
Epoch 389/1000
- 0s - loss: 2.2098 - acc: 0.2609
Epoch 390/1000
- 0s - loss: 2.2087 - acc: 0.2609
Epoch 391/1000
- 0s - loss: 2.2071 - acc: 0.2609
Epoch 392/1000
- 0s - loss: 2.2063 - acc: 0.2609
Epoch 393/1000
- 0s - loss: 2.2051 - acc: 0.2609
Epoch 394/1000
- 0s - loss: 2.2039 - acc: 0.2609
Epoch 395/1000
- 0s - loss: 2.2025 - acc: 0.3043
Epoch 396/1000
- 0s - loss: 2.2014 - acc: 0.3043
Epoch 397/1000
- 0s - loss: 2.2003 - acc: 0.3043
Epoch 398/1000
- 0s - loss: 2.1987 - acc: 0.3043
Epoch 399/1000
- 0s - loss: 2.1975 - acc: 0.3043
Epoch 400/1000
- 0s - loss: 2.1964 - acc: 0.3043
Epoch 401/1000
- 0s - loss: 2.1952 - acc: 0.2609
Epoch 402/1000
- 0s - loss: 2.1939 - acc: 0.3478
Epoch 403/1000
- 0s - loss: 2.1931 - acc: 0.3478
Epoch 404/1000
- 0s - loss: 2.1917 - acc: 0.3478
Epoch 405/1000
- 0s - loss: 2.1909 - acc: 0.3478
Epoch 406/1000
- 0s - loss: 2.1889 - acc: 0.3913
Epoch 407/1000
- 0s - loss: 2.1872 - acc: 0.3913
Epoch 408/1000
- 0s - loss: 2.1864 - acc: 0.3913
Epoch 409/1000
- 0s - loss: 2.1855 - acc: 0.3478
Epoch 410/1000
- 0s - loss: 2.1845 - acc: 0.3478
Epoch 411/1000
- 0s - loss: 2.1833 - acc: 0.3043
Epoch 412/1000
- 0s - loss: 2.1818 - acc: 0.3043
Epoch 413/1000
- 0s - loss: 2.1809 - acc: 0.3913
Epoch 414/1000
- 0s - loss: 2.1793 - acc: 0.3913
Epoch 415/1000
- 0s - loss: 2.1783 - acc: 0.3913
Epoch 416/1000
- 0s - loss: 2.1774 - acc: 0.3913
Epoch 417/1000
- 0s - loss: 2.1760 - acc: 0.3478
Epoch 418/1000
- 0s - loss: 2.1748 - acc: 0.3478
Epoch 419/1000
- 0s - loss: 2.1728 - acc: 0.3913
Epoch 420/1000
- 0s - loss: 2.1720 - acc: 0.3913
Epoch 421/1000
- 0s - loss: 2.1710 - acc: 0.3913
Epoch 422/1000
- 0s - loss: 2.1697 - acc: 0.3478
Epoch 423/1000
- 0s - loss: 2.1691 - acc: 0.3043
Epoch 424/1000
- 0s - loss: 2.1683 - acc: 0.3043
Epoch 425/1000
- 0s - loss: 2.1665 - acc: 0.3043
Epoch 426/1000
- 0s - loss: 2.1649 - acc: 0.3043
Epoch 427/1000
- 0s - loss: 2.1638 - acc: 0.3043
Epoch 428/1000
- 0s - loss: 2.1636 - acc: 0.3043
Epoch 429/1000
- 0s - loss: 2.1616 - acc: 0.2609
Epoch 430/1000
- 0s - loss: 2.1613 - acc: 0.2609
Epoch 431/1000
- 0s - loss: 2.1594 - acc: 0.3043
Epoch 432/1000
- 0s - loss: 2.1583 - acc: 0.2609
Epoch 433/1000
- 0s - loss: 2.1577 - acc: 0.2609
Epoch 434/1000
- 0s - loss: 2.1565 - acc: 0.2609
Epoch 435/1000
- 0s - loss: 2.1548 - acc: 0.3478
Epoch 436/1000
- 0s - loss: 2.1540 - acc: 0.3478
Epoch 437/1000
- 0s - loss: 2.1530 - acc: 0.3043
Epoch 438/1000
- 0s - loss: 2.1516 - acc: 0.3043
Epoch 439/1000
- 0s - loss: 2.1507 - acc: 0.3043
Epoch 440/1000
- 0s - loss: 2.1492 - acc: 0.3043
Epoch 441/1000
- 0s - loss: 2.1482 - acc: 0.3478
Epoch 442/1000
- 0s - loss: 2.1472 - acc: 0.3043
Epoch 443/1000
- 0s - loss: 2.1463 - acc: 0.2609
Epoch 444/1000
- 0s - loss: 2.1451 - acc: 0.2609
Epoch 445/1000
- 0s - loss: 2.1442 - acc: 0.2609
Epoch 446/1000
- 0s - loss: 2.1427 - acc: 0.2609
Epoch 447/1000
- 0s - loss: 2.1419 - acc: 0.2609
Epoch 448/1000
- 0s - loss: 2.1408 - acc: 0.2609
Epoch 449/1000
- 0s - loss: 2.1398 - acc: 0.3043
Epoch 450/1000
- 0s - loss: 2.1390 - acc: 0.3043
Epoch 451/1000
- 0s - loss: 2.1379 - acc: 0.3043
Epoch 452/1000
- 0s - loss: 2.1373 - acc: 0.3478
Epoch 453/1000
- 0s - loss: 2.1356 - acc: 0.3478
Epoch 454/1000
- 0s - loss: 2.1344 - acc: 0.3478
Epoch 455/1000
- 0s - loss: 2.1334 - acc: 0.3478
Epoch 456/1000
- 0s - loss: 2.1323 - acc: 0.3478
Epoch 457/1000
- 0s - loss: 2.1311 - acc: 0.3478
Epoch 458/1000
- 0s - loss: 2.1303 - acc: 0.3478
Epoch 459/1000
- 0s - loss: 2.1290 - acc: 0.3913
Epoch 460/1000
- 0s - loss: 2.1290 - acc: 0.3913
Epoch 461/1000
- 0s - loss: 2.1275 - acc: 0.3913
Epoch 462/1000
- 0s - loss: 2.1268 - acc: 0.3913
Epoch 463/1000
- 0s - loss: 2.1254 - acc: 0.3913
Epoch 464/1000
- 0s - loss: 2.1248 - acc: 0.3478
Epoch 465/1000
- 0s - loss: 2.1233 - acc: 0.3478
Epoch 466/1000
- 0s - loss: 2.1217 - acc: 0.3478
Epoch 467/1000
- 0s - loss: 2.1209 - acc: 0.3478
Epoch 468/1000
- 0s - loss: 2.1197 - acc: 0.3478
Epoch 469/1000
- 0s - loss: 2.1190 - acc: 0.3478
Epoch 470/1000
- 0s - loss: 2.1176 - acc: 0.3478
Epoch 471/1000
- 0s - loss: 2.1166 - acc: 0.3478
Epoch 472/1000
- 0s - loss: 2.1158 - acc: 0.3913
Epoch 473/1000
- 0s - loss: 2.1149 - acc: 0.3913
Epoch 474/1000
- 0s - loss: 2.1135 - acc: 0.4348
Epoch 475/1000
- 0s - loss: 2.1131 - acc: 0.3913
Epoch 476/1000
- 0s - loss: 2.1111 - acc: 0.3478
Epoch 477/1000
- 0s - loss: 2.1099 - acc: 0.3478
Epoch 478/1000
- 0s - loss: 2.1093 - acc: 0.3478
Epoch 479/1000
- 0s - loss: 2.1085 - acc: 0.3478
Epoch 480/1000
- 0s - loss: 2.1074 - acc: 0.3478
Epoch 481/1000
- 0s - loss: 2.1064 - acc: 0.3478
Epoch 482/1000
- 0s - loss: 2.1057 - acc: 0.3478
Epoch 483/1000
- 0s - loss: 2.1044 - acc: 0.3478
Epoch 484/1000
- 0s - loss: 2.1031 - acc: 0.3478
Epoch 485/1000
- 0s - loss: 2.1026 - acc: 0.3478
Epoch 486/1000
- 0s - loss: 2.1018 - acc: 0.3478
Epoch 487/1000
*** WARNING: skipped 1250 bytes of output ***
- 0s - loss: 2.0758 - acc: 0.3478
Epoch 513/1000
- 0s - loss: 2.0741 - acc: 0.3478
Epoch 514/1000
- 0s - loss: 2.0739 - acc: 0.3478
Epoch 515/1000
- 0s - loss: 2.0735 - acc: 0.4348
Epoch 516/1000
- 0s - loss: 2.0723 - acc: 0.3478
Epoch 517/1000
- 0s - loss: 2.0711 - acc: 0.3913
Epoch 518/1000
- 0s - loss: 2.0699 - acc: 0.3478
Epoch 519/1000
- 0s - loss: 2.0691 - acc: 0.3913
Epoch 520/1000
- 0s - loss: 2.0681 - acc: 0.3913
Epoch 521/1000
- 0s - loss: 2.0679 - acc: 0.3913
Epoch 522/1000
- 0s - loss: 2.0664 - acc: 0.3913
Epoch 523/1000
- 0s - loss: 2.0655 - acc: 0.3913
Epoch 524/1000
- 0s - loss: 2.0643 - acc: 0.3913
Epoch 525/1000
- 0s - loss: 2.0632 - acc: 0.3478
Epoch 526/1000
- 0s - loss: 2.0621 - acc: 0.3913
Epoch 527/1000
- 0s - loss: 2.0618 - acc: 0.3478
Epoch 528/1000
- 0s - loss: 2.0610 - acc: 0.3478
Epoch 529/1000
- 0s - loss: 2.0601 - acc: 0.3478
Epoch 530/1000
- 0s - loss: 2.0585 - acc: 0.3478
Epoch 531/1000
- 0s - loss: 2.0578 - acc: 0.3913
Epoch 532/1000
- 0s - loss: 2.0568 - acc: 0.3913
Epoch 533/1000
- 0s - loss: 2.0561 - acc: 0.4348
Epoch 534/1000
- 0s - loss: 2.0554 - acc: 0.4783
Epoch 535/1000
- 0s - loss: 2.0546 - acc: 0.3913
Epoch 536/1000
- 0s - loss: 2.0535 - acc: 0.3913
Epoch 537/1000
- 0s - loss: 2.0527 - acc: 0.3913
Epoch 538/1000
- 0s - loss: 2.0520 - acc: 0.3913
Epoch 539/1000
- 0s - loss: 2.0507 - acc: 0.3913
Epoch 540/1000
- 0s - loss: 2.0493 - acc: 0.3913
Epoch 541/1000
- 0s - loss: 2.0489 - acc: 0.4783
Epoch 542/1000
- 0s - loss: 2.0478 - acc: 0.4783
Epoch 543/1000
- 0s - loss: 2.0464 - acc: 0.4783
Epoch 544/1000
- 0s - loss: 2.0468 - acc: 0.4783
Epoch 545/1000
- 0s - loss: 2.0455 - acc: 0.5217
Epoch 546/1000
- 0s - loss: 2.0441 - acc: 0.5652
Epoch 547/1000
- 0s - loss: 2.0431 - acc: 0.5652
Epoch 548/1000
- 0s - loss: 2.0423 - acc: 0.5652
Epoch 549/1000
- 0s - loss: 2.0412 - acc: 0.5652
Epoch 550/1000
- 0s - loss: 2.0405 - acc: 0.5652
Epoch 551/1000
- 0s - loss: 2.0399 - acc: 0.5217
Epoch 552/1000
- 0s - loss: 2.0390 - acc: 0.5217
Epoch 553/1000
- 0s - loss: 2.0379 - acc: 0.5217
Epoch 554/1000
- 0s - loss: 2.0372 - acc: 0.5217
Epoch 555/1000
- 0s - loss: 2.0367 - acc: 0.5217
Epoch 556/1000
- 0s - loss: 2.0357 - acc: 0.5217
Epoch 557/1000
- 0s - loss: 2.0351 - acc: 0.4783
Epoch 558/1000
- 0s - loss: 2.0340 - acc: 0.4783
Epoch 559/1000
- 0s - loss: 2.0329 - acc: 0.5652
Epoch 560/1000
- 0s - loss: 2.0324 - acc: 0.5652
Epoch 561/1000
- 0s - loss: 2.0316 - acc: 0.5217
Epoch 562/1000
- 0s - loss: 2.0308 - acc: 0.5217
Epoch 563/1000
- 0s - loss: 2.0296 - acc: 0.5217
Epoch 564/1000
- 0s - loss: 2.0288 - acc: 0.5217
Epoch 565/1000
- 0s - loss: 2.0272 - acc: 0.5217
Epoch 566/1000
- 0s - loss: 2.0271 - acc: 0.4783
Epoch 567/1000
- 0s - loss: 2.0262 - acc: 0.4348
Epoch 568/1000
- 0s - loss: 2.0248 - acc: 0.4348
Epoch 569/1000
- 0s - loss: 2.0243 - acc: 0.4783
Epoch 570/1000
- 0s - loss: 2.0235 - acc: 0.5217
Epoch 571/1000
- 0s - loss: 2.0224 - acc: 0.5217
Epoch 572/1000
- 0s - loss: 2.0214 - acc: 0.5217
Epoch 573/1000
- 0s - loss: 2.0212 - acc: 0.4783
Epoch 574/1000
- 0s - loss: 2.0197 - acc: 0.4783
Epoch 575/1000
- 0s - loss: 2.0192 - acc: 0.5217
Epoch 576/1000
- 0s - loss: 2.0186 - acc: 0.5217
Epoch 577/1000
- 0s - loss: 2.0175 - acc: 0.4783
Epoch 578/1000
- 0s - loss: 2.0164 - acc: 0.4783
Epoch 579/1000
- 0s - loss: 2.0155 - acc: 0.4348
Epoch 580/1000
- 0s - loss: 2.0142 - acc: 0.4348
Epoch 581/1000
- 0s - loss: 2.0139 - acc: 0.4783
Epoch 582/1000
- 0s - loss: 2.0128 - acc: 0.4783
Epoch 583/1000
- 0s - loss: 2.0121 - acc: 0.4783
Epoch 584/1000
- 0s - loss: 2.0109 - acc: 0.5217
Epoch 585/1000
- 0s - loss: 2.0109 - acc: 0.4783
Epoch 586/1000
- 0s - loss: 2.0092 - acc: 0.4783
Epoch 587/1000
- 0s - loss: 2.0086 - acc: 0.4348
Epoch 588/1000
- 0s - loss: 2.0086 - acc: 0.5217
Epoch 589/1000
- 0s - loss: 2.0069 - acc: 0.5217
Epoch 590/1000
- 0s - loss: 2.0059 - acc: 0.4783
Epoch 591/1000
- 0s - loss: 2.0048 - acc: 0.4783
Epoch 592/1000
- 0s - loss: 2.0052 - acc: 0.4348
Epoch 593/1000
- 0s - loss: 2.0037 - acc: 0.3913
Epoch 594/1000
- 0s - loss: 2.0030 - acc: 0.4348
Epoch 595/1000
- 0s - loss: 2.0018 - acc: 0.4348
Epoch 596/1000
- 0s - loss: 2.0010 - acc: 0.4348
Epoch 597/1000
- 0s - loss: 2.0008 - acc: 0.5217
Epoch 598/1000
- 0s - loss: 1.9992 - acc: 0.5217
Epoch 599/1000
- 0s - loss: 1.9989 - acc: 0.4783
Epoch 600/1000
- 0s - loss: 1.9977 - acc: 0.4348
Epoch 601/1000
- 0s - loss: 1.9977 - acc: 0.4783
Epoch 602/1000
- 0s - loss: 1.9965 - acc: 0.4783
Epoch 603/1000
- 0s - loss: 1.9963 - acc: 0.5217
Epoch 604/1000
- 0s - loss: 1.9944 - acc: 0.5217
Epoch 605/1000
- 0s - loss: 1.9944 - acc: 0.5217
Epoch 606/1000
- 0s - loss: 1.9932 - acc: 0.5217
Epoch 607/1000
- 0s - loss: 1.9923 - acc: 0.5652
Epoch 608/1000
- 0s - loss: 1.9916 - acc: 0.5652
Epoch 609/1000
- 0s - loss: 1.9903 - acc: 0.5217
Epoch 610/1000
- 0s - loss: 1.9894 - acc: 0.5652
Epoch 611/1000
- 0s - loss: 1.9904 - acc: 0.5652
Epoch 612/1000
- 0s - loss: 1.9887 - acc: 0.5217
Epoch 613/1000
- 0s - loss: 1.9882 - acc: 0.5217
Epoch 614/1000
- 0s - loss: 1.9866 - acc: 0.5652
Epoch 615/1000
- 0s - loss: 1.9864 - acc: 0.5652
Epoch 616/1000
- 0s - loss: 1.9860 - acc: 0.5652
Epoch 617/1000
- 0s - loss: 1.9850 - acc: 0.5652
Epoch 618/1000
- 0s - loss: 1.9840 - acc: 0.5652
Epoch 619/1000
- 0s - loss: 1.9833 - acc: 0.5652
Epoch 620/1000
- 0s - loss: 1.9828 - acc: 0.5652
Epoch 621/1000
- 0s - loss: 1.9816 - acc: 0.5652
Epoch 622/1000
- 0s - loss: 1.9811 - acc: 0.5217
Epoch 623/1000
- 0s - loss: 1.9803 - acc: 0.5652
Epoch 624/1000
- 0s - loss: 1.9790 - acc: 0.5217
Epoch 625/1000
- 0s - loss: 1.9780 - acc: 0.5217
Epoch 626/1000
- 0s - loss: 1.9784 - acc: 0.5217
Epoch 627/1000
- 0s - loss: 1.9765 - acc: 0.5217
Epoch 628/1000
- 0s - loss: 1.9759 - acc: 0.5217
Epoch 629/1000
- 0s - loss: 1.9754 - acc: 0.4783
Epoch 630/1000
- 0s - loss: 1.9745 - acc: 0.4783
Epoch 631/1000
- 0s - loss: 1.9744 - acc: 0.5217
Epoch 632/1000
- 0s - loss: 1.9726 - acc: 0.5217
Epoch 633/1000
- 0s - loss: 1.9718 - acc: 0.5217
Epoch 634/1000
- 0s - loss: 1.9712 - acc: 0.5217
Epoch 635/1000
- 0s - loss: 1.9702 - acc: 0.5217
Epoch 636/1000
- 0s - loss: 1.9701 - acc: 0.5217
Epoch 637/1000
- 0s - loss: 1.9690 - acc: 0.5217
Epoch 638/1000
- 0s - loss: 1.9686 - acc: 0.5217
Epoch 639/1000
- 0s - loss: 1.9680 - acc: 0.5652
Epoch 640/1000
- 0s - loss: 1.9667 - acc: 0.5217
Epoch 641/1000
- 0s - loss: 1.9663 - acc: 0.5217
Epoch 642/1000
- 0s - loss: 1.9652 - acc: 0.5652
Epoch 643/1000
- 0s - loss: 1.9646 - acc: 0.5652
Epoch 644/1000
- 0s - loss: 1.9638 - acc: 0.5217
Epoch 645/1000
- 0s - loss: 1.9632 - acc: 0.5652
Epoch 646/1000
- 0s - loss: 1.9622 - acc: 0.5652
Epoch 647/1000
- 0s - loss: 1.9619 - acc: 0.5652
Epoch 648/1000
- 0s - loss: 1.9605 - acc: 0.5652
Epoch 649/1000
- 0s - loss: 1.9607 - acc: 0.5217
Epoch 650/1000
- 0s - loss: 1.9586 - acc: 0.4783
Epoch 651/1000
- 0s - loss: 1.9589 - acc: 0.4783
Epoch 652/1000
- 0s - loss: 1.9573 - acc: 0.4348
Epoch 653/1000
- 0s - loss: 1.9573 - acc: 0.5217
Epoch 654/1000
- 0s - loss: 1.9571 - acc: 0.5217
Epoch 655/1000
- 0s - loss: 1.9556 - acc: 0.5652
Epoch 656/1000
- 0s - loss: 1.9545 - acc: 0.5217
Epoch 657/1000
- 0s - loss: 1.9543 - acc: 0.5217
Epoch 658/1000
- 0s - loss: 1.9543 - acc: 0.4783
Epoch 659/1000
- 0s - loss: 1.9529 - acc: 0.5652
Epoch 660/1000
- 0s - loss: 1.9521 - acc: 0.5652
Epoch 661/1000
- 0s - loss: 1.9511 - acc: 0.5217
Epoch 662/1000
- 0s - loss: 1.9504 - acc: 0.6087
Epoch 663/1000
- 0s - loss: 1.9493 - acc: 0.6087
Epoch 664/1000
- 0s - loss: 1.9492 - acc: 0.6087
Epoch 665/1000
- 0s - loss: 1.9488 - acc: 0.5652
Epoch 666/1000
- 0s - loss: 1.9474 - acc: 0.5217
Epoch 667/1000
- 0s - loss: 1.9467 - acc: 0.4783
Epoch 668/1000
- 0s - loss: 1.9457 - acc: 0.4783
Epoch 669/1000
- 0s - loss: 1.9451 - acc: 0.4783
Epoch 670/1000
- 0s - loss: 1.9440 - acc: 0.4783
Epoch 671/1000
- 0s - loss: 1.9443 - acc: 0.3913
Epoch 672/1000
- 0s - loss: 1.9431 - acc: 0.5217
Epoch 673/1000
- 0s - loss: 1.9421 - acc: 0.5217
Epoch 674/1000
- 0s - loss: 1.9412 - acc: 0.5217
Epoch 675/1000
- 0s - loss: 1.9410 - acc: 0.5217
Epoch 676/1000
- 0s - loss: 1.9401 - acc: 0.4783
Epoch 677/1000
- 0s - loss: 1.9392 - acc: 0.5217
Epoch 678/1000
- 0s - loss: 1.9390 - acc: 0.5652
Epoch 679/1000
- 0s - loss: 1.9385 - acc: 0.4783
Epoch 680/1000
- 0s - loss: 1.9369 - acc: 0.4783
Epoch 681/1000
- 0s - loss: 1.9367 - acc: 0.5217
Epoch 682/1000
- 0s - loss: 1.9356 - acc: 0.4783
Epoch 683/1000
- 0s - loss: 1.9348 - acc: 0.4348
Epoch 684/1000
- 0s - loss: 1.9347 - acc: 0.4783
Epoch 685/1000
- 0s - loss: 1.9337 - acc: 0.4783
Epoch 686/1000
- 0s - loss: 1.9332 - acc: 0.5217
Epoch 687/1000
- 0s - loss: 1.9322 - acc: 0.5217
Epoch 688/1000
- 0s - loss: 1.9316 - acc: 0.5217
Epoch 689/1000
- 0s - loss: 1.9304 - acc: 0.6087
Epoch 690/1000
- 0s - loss: 1.9302 - acc: 0.5652
Epoch 691/1000
- 0s - loss: 1.9303 - acc: 0.5652
Epoch 692/1000
- 0s - loss: 1.9289 - acc: 0.5217
Epoch 693/1000
- 0s - loss: 1.9283 - acc: 0.5217
Epoch 694/1000
- 0s - loss: 1.9279 - acc: 0.4783
Epoch 695/1000
- 0s - loss: 1.9264 - acc: 0.4783
Epoch 696/1000
- 0s - loss: 1.9262 - acc: 0.5217
Epoch 697/1000
- 0s - loss: 1.9251 - acc: 0.5217
Epoch 698/1000
- 0s - loss: 1.9245 - acc: 0.4783
Epoch 699/1000
- 0s - loss: 1.9236 - acc: 0.4783
Epoch 700/1000
- 0s - loss: 1.9231 - acc: 0.4783
Epoch 701/1000
- 0s - loss: 1.9227 - acc: 0.5217
Epoch 702/1000
- 0s - loss: 1.9214 - acc: 0.5217
Epoch 703/1000
- 0s - loss: 1.9203 - acc: 0.5217
Epoch 704/1000
- 0s - loss: 1.9208 - acc: 0.5217
Epoch 705/1000
- 0s - loss: 1.9194 - acc: 0.5217
Epoch 706/1000
- 0s - loss: 1.9194 - acc: 0.5217
Epoch 707/1000
- 0s - loss: 1.9185 - acc: 0.5217
Epoch 708/1000
- 0s - loss: 1.9172 - acc: 0.4783
Epoch 709/1000
- 0s - loss: 1.9171 - acc: 0.5217
Epoch 710/1000
- 0s - loss: 1.9154 - acc: 0.5652
Epoch 711/1000
- 0s - loss: 1.9153 - acc: 0.5652
Epoch 712/1000
- 0s - loss: 1.9151 - acc: 0.5652
Epoch 713/1000
- 0s - loss: 1.9141 - acc: 0.5652
Epoch 714/1000
- 0s - loss: 1.9139 - acc: 0.5652
Epoch 715/1000
- 0s - loss: 1.9134 - acc: 0.6087
Epoch 716/1000
- 0s - loss: 1.9132 - acc: 0.6087
Epoch 717/1000
- 0s - loss: 1.9114 - acc: 0.5652
Epoch 718/1000
- 0s - loss: 1.9112 - acc: 0.5652
Epoch 719/1000
- 0s - loss: 1.9106 - acc: 0.5652
Epoch 720/1000
- 0s - loss: 1.9098 - acc: 0.5217
Epoch 721/1000
- 0s - loss: 1.9093 - acc: 0.6087
Epoch 722/1000
- 0s - loss: 1.9093 - acc: 0.5217
Epoch 723/1000
- 0s - loss: 1.9075 - acc: 0.5217
Epoch 724/1000
- 0s - loss: 1.9066 - acc: 0.6087
Epoch 725/1000
- 0s - loss: 1.9064 - acc: 0.6087
Epoch 726/1000
- 0s - loss: 1.9062 - acc: 0.6087
Epoch 727/1000
- 0s - loss: 1.9051 - acc: 0.6522
Epoch 728/1000
- 0s - loss: 1.9043 - acc: 0.6522
Epoch 729/1000
- 0s - loss: 1.9032 - acc: 0.6522
Epoch 730/1000
- 0s - loss: 1.9031 - acc: 0.6522
Epoch 731/1000
- 0s - loss: 1.9023 - acc: 0.6522
Epoch 732/1000
- 0s - loss: 1.9012 - acc: 0.6522
Epoch 733/1000
- 0s - loss: 1.9008 - acc: 0.6087
Epoch 734/1000
- 0s - loss: 1.9000 - acc: 0.6087
Epoch 735/1000
- 0s - loss: 1.8994 - acc: 0.6522
Epoch 736/1000
- 0s - loss: 1.8992 - acc: 0.6522
Epoch 737/1000
- 0s - loss: 1.8985 - acc: 0.6522
Epoch 738/1000
- 0s - loss: 1.8976 - acc: 0.6522
Epoch 739/1000
- 0s - loss: 1.8973 - acc: 0.6087
Epoch 740/1000
- 0s - loss: 1.8952 - acc: 0.6087
Epoch 741/1000
- 0s - loss: 1.8955 - acc: 0.5652
Epoch 742/1000
- 0s - loss: 1.8949 - acc: 0.5217
Epoch 743/1000
- 0s - loss: 1.8940 - acc: 0.5217
Epoch 744/1000
- 0s - loss: 1.8938 - acc: 0.5217
Epoch 745/1000
- 0s - loss: 1.8930 - acc: 0.5217
Epoch 746/1000
- 0s - loss: 1.8921 - acc: 0.4783
Epoch 747/1000
- 0s - loss: 1.8921 - acc: 0.4783
Epoch 748/1000
- 0s - loss: 1.8911 - acc: 0.4783
Epoch 749/1000
- 0s - loss: 1.8902 - acc: 0.5217
Epoch 750/1000
- 0s - loss: 1.8893 - acc: 0.5652
Epoch 751/1000
- 0s - loss: 1.8895 - acc: 0.5652
Epoch 752/1000
- 0s - loss: 1.8886 - acc: 0.5652
Epoch 753/1000
- 0s - loss: 1.8882 - acc: 0.5652
Epoch 754/1000
- 0s - loss: 1.8871 - acc: 0.5652
Epoch 755/1000
- 0s - loss: 1.8872 - acc: 0.5652
Epoch 756/1000
- 0s - loss: 1.8865 - acc: 0.5652
Epoch 757/1000
- 0s - loss: 1.8859 - acc: 0.6087
Epoch 758/1000
- 0s - loss: 1.8841 - acc: 0.5652
Epoch 759/1000
- 0s - loss: 1.8840 - acc: 0.5217
Epoch 760/1000
- 0s - loss: 1.8832 - acc: 0.5217
Epoch 761/1000
- 0s - loss: 1.8830 - acc: 0.5217
Epoch 762/1000
- 0s - loss: 1.8814 - acc: 0.5217
Epoch 763/1000
- 0s - loss: 1.8818 - acc: 0.5217
Epoch 764/1000
- 0s - loss: 1.8811 - acc: 0.4783
Epoch 765/1000
- 0s - loss: 1.8808 - acc: 0.4783
Epoch 766/1000
- 0s - loss: 1.8803 - acc: 0.4783
Epoch 767/1000
- 0s - loss: 1.8791 - acc: 0.4783
Epoch 768/1000
- 0s - loss: 1.8785 - acc: 0.4783
Epoch 769/1000
- 0s - loss: 1.8778 - acc: 0.4783
Epoch 770/1000
- 0s - loss: 1.8767 - acc: 0.4783
Epoch 771/1000
- 0s - loss: 1.8768 - acc: 0.5217
Epoch 772/1000
- 0s - loss: 1.8763 - acc: 0.5217
Epoch 773/1000
- 0s - loss: 1.8758 - acc: 0.5652
Epoch 774/1000
- 0s - loss: 1.8746 - acc: 0.6087
Epoch 775/1000
- 0s - loss: 1.8738 - acc: 0.6087
Epoch 776/1000
- 0s - loss: 1.8737 - acc: 0.5652
Epoch 777/1000
- 0s - loss: 1.8731 - acc: 0.6087
Epoch 778/1000
- 0s - loss: 1.8720 - acc: 0.6087
Epoch 779/1000
- 0s - loss: 1.8718 - acc: 0.6087
Epoch 780/1000
- 0s - loss: 1.8712 - acc: 0.6522
Epoch 781/1000
- 0s - loss: 1.8703 - acc: 0.6087
Epoch 782/1000
- 0s - loss: 1.8698 - acc: 0.6522
Epoch 783/1000
- 0s - loss: 1.8688 - acc: 0.6522
Epoch 784/1000
- 0s - loss: 1.8681 - acc: 0.6522
Epoch 785/1000
- 0s - loss: 1.8677 - acc: 0.6522
Epoch 786/1000
- 0s - loss: 1.8668 - acc: 0.6522
Epoch 787/1000
- 0s - loss: 1.8661 - acc: 0.6522
Epoch 788/1000
- 0s - loss: 1.8653 - acc: 0.6522
Epoch 789/1000
- 0s - loss: 1.8651 - acc: 0.6522
Epoch 790/1000
- 0s - loss: 1.8649 - acc: 0.6087
Epoch 791/1000
- 0s - loss: 1.8644 - acc: 0.6087
Epoch 792/1000
- 0s - loss: 1.8628 - acc: 0.6522
Epoch 793/1000
- 0s - loss: 1.8625 - acc: 0.6522
Epoch 794/1000
- 0s - loss: 1.8624 - acc: 0.6087
Epoch 795/1000
- 0s - loss: 1.8621 - acc: 0.5652
Epoch 796/1000
- 0s - loss: 1.8610 - acc: 0.5217
Epoch 797/1000
- 0s - loss: 1.8601 - acc: 0.5652
Epoch 798/1000
- 0s - loss: 1.8592 - acc: 0.5217
Epoch 799/1000
- 0s - loss: 1.8583 - acc: 0.5652
Epoch 800/1000
- 0s - loss: 1.8575 - acc: 0.5652
Epoch 801/1000
- 0s - loss: 1.8568 - acc: 0.6087
Epoch 802/1000
- 0s - loss: 1.8575 - acc: 0.6087
Epoch 803/1000
- 0s - loss: 1.8568 - acc: 0.5652
Epoch 804/1000
- 0s - loss: 1.8560 - acc: 0.5652
Epoch 805/1000
- 0s - loss: 1.8554 - acc: 0.5652
Epoch 806/1000
- 0s - loss: 1.8547 - acc: 0.5652
Epoch 807/1000
- 0s - loss: 1.8549 - acc: 0.5217
Epoch 808/1000
- 0s - loss: 1.8532 - acc: 0.5217
Epoch 809/1000
- 0s - loss: 1.8533 - acc: 0.5652
Epoch 810/1000
- 0s - loss: 1.8526 - acc: 0.5217
Epoch 811/1000
- 0s - loss: 1.8517 - acc: 0.5217
Epoch 812/1000
- 0s - loss: 1.8509 - acc: 0.6087
Epoch 813/1000
- 0s - loss: 1.8508 - acc: 0.6087
Epoch 814/1000
- 0s - loss: 1.8507 - acc: 0.6087
Epoch 815/1000
- 0s - loss: 1.8493 - acc: 0.6522
Epoch 816/1000
- 0s - loss: 1.8486 - acc: 0.6087
Epoch 817/1000
- 0s - loss: 1.8482 - acc: 0.6087
Epoch 818/1000
- 0s - loss: 1.8471 - acc: 0.6087
Epoch 819/1000
- 0s - loss: 1.8472 - acc: 0.6522
Epoch 820/1000
- 0s - loss: 1.8463 - acc: 0.6522
Epoch 821/1000
- 0s - loss: 1.8453 - acc: 0.6957
Epoch 822/1000
- 0s - loss: 1.8462 - acc: 0.6957
Epoch 823/1000
- 0s - loss: 1.8444 - acc: 0.6957
Epoch 824/1000
- 0s - loss: 1.8432 - acc: 0.6522
Epoch 825/1000
- 0s - loss: 1.8428 - acc: 0.6522
Epoch 826/1000
- 0s - loss: 1.8431 - acc: 0.5217
Epoch 827/1000
- 0s - loss: 1.8427 - acc: 0.5217
Epoch 828/1000
- 0s - loss: 1.8416 - acc: 0.5652
Epoch 829/1000
- 0s - loss: 1.8404 - acc: 0.6087
Epoch 830/1000
- 0s - loss: 1.8397 - acc: 0.6087
Epoch 831/1000
- 0s - loss: 1.8404 - acc: 0.6087
Epoch 832/1000
- 0s - loss: 1.8392 - acc: 0.6087
Epoch 833/1000
- 0s - loss: 1.8382 - acc: 0.6522
Epoch 834/1000
- 0s - loss: 1.8382 - acc: 0.6087
Epoch 835/1000
- 0s - loss: 1.8373 - acc: 0.6522
Epoch 836/1000
- 0s - loss: 1.8370 - acc: 0.6087
Epoch 837/1000
- 0s - loss: 1.8364 - acc: 0.6087
Epoch 838/1000
- 0s - loss: 1.8356 - acc: 0.5652
Epoch 839/1000
- 0s - loss: 1.8356 - acc: 0.6087
Epoch 840/1000
- 0s - loss: 1.8341 - acc: 0.6522
Epoch 841/1000
- 0s - loss: 1.8336 - acc: 0.6522
Epoch 842/1000
- 0s - loss: 1.8339 - acc: 0.5652
Epoch 843/1000
- 0s - loss: 1.8329 - acc: 0.5652
Epoch 844/1000
- 0s - loss: 1.8320 - acc: 0.5652
Epoch 845/1000
- 0s - loss: 1.8314 - acc: 0.6087
Epoch 846/1000
- 0s - loss: 1.8317 - acc: 0.5652
Epoch 847/1000
- 0s - loss: 1.8308 - acc: 0.6087
Epoch 848/1000
- 0s - loss: 1.8296 - acc: 0.5652
Epoch 849/1000
- 0s - loss: 1.8292 - acc: 0.5652
Epoch 850/1000
- 0s - loss: 1.8291 - acc: 0.5217
Epoch 851/1000
- 0s - loss: 1.8282 - acc: 0.5652
Epoch 852/1000
- 0s - loss: 1.8274 - acc: 0.5652
Epoch 853/1000
- 0s - loss: 1.8273 - acc: 0.5217
Epoch 854/1000
- 0s - loss: 1.8261 - acc: 0.5217
Epoch 855/1000
- 0s - loss: 1.8251 - acc: 0.5217
Epoch 856/1000
- 0s - loss: 1.8253 - acc: 0.5652
Epoch 857/1000
- 0s - loss: 1.8255 - acc: 0.5652
Epoch 858/1000
- 0s - loss: 1.8241 - acc: 0.5217
Epoch 859/1000
- 0s - loss: 1.8241 - acc: 0.5652
Epoch 860/1000
- 0s - loss: 1.8235 - acc: 0.5217
Epoch 861/1000
- 0s - loss: 1.8231 - acc: 0.5652
Epoch 862/1000
- 0s - loss: 1.8218 - acc: 0.6522
Epoch 863/1000
- 0s - loss: 1.8218 - acc: 0.6087
Epoch 864/1000
- 0s - loss: 1.8212 - acc: 0.5652
Epoch 865/1000
- 0s - loss: 1.8201 - acc: 0.6522
Epoch 866/1000
- 0s - loss: 1.8199 - acc: 0.6522
Epoch 867/1000
- 0s - loss: 1.8194 - acc: 0.6087
Epoch 868/1000
- 0s - loss: 1.8191 - acc: 0.6087
Epoch 869/1000
- 0s - loss: 1.8187 - acc: 0.6087
Epoch 870/1000
- 0s - loss: 1.8175 - acc: 0.5652
Epoch 871/1000
- 0s - loss: 1.8171 - acc: 0.5217
Epoch 872/1000
- 0s - loss: 1.8171 - acc: 0.5217
Epoch 873/1000
- 0s - loss: 1.8157 - acc: 0.4783
Epoch 874/1000
- 0s - loss: 1.8148 - acc: 0.5652
Epoch 875/1000
- 0s - loss: 1.8137 - acc: 0.5652
Epoch 876/1000
- 0s - loss: 1.8136 - acc: 0.6522
Epoch 877/1000
- 0s - loss: 1.8134 - acc: 0.6522
Epoch 878/1000
- 0s - loss: 1.8133 - acc: 0.7391
Epoch 879/1000
- 0s - loss: 1.8125 - acc: 0.6957
Epoch 880/1000
- 0s - loss: 1.8116 - acc: 0.6522
Epoch 881/1000
- 0s - loss: 1.8112 - acc: 0.6522
Epoch 882/1000
- 0s - loss: 1.8099 - acc: 0.6957
Epoch 883/1000
- 0s - loss: 1.8102 - acc: 0.6522
Epoch 884/1000
- 0s - loss: 1.8099 - acc: 0.6522
Epoch 885/1000
- 0s - loss: 1.8087 - acc: 0.6522
Epoch 886/1000
- 0s - loss: 1.8087 - acc: 0.5652
Epoch 887/1000
- 0s - loss: 1.8071 - acc: 0.5652
Epoch 888/1000
- 0s - loss: 1.8074 - acc: 0.5652
Epoch 889/1000
- 0s - loss: 1.8069 - acc: 0.5652
Epoch 890/1000
- 0s - loss: 1.8064 - acc: 0.6087
Epoch 891/1000
- 0s - loss: 1.8054 - acc: 0.6087
Epoch 892/1000
- 0s - loss: 1.8052 - acc: 0.6087
Epoch 893/1000
- 0s - loss: 1.8042 - acc: 0.6522
Epoch 894/1000
- 0s - loss: 1.8048 - acc: 0.6087
Epoch 895/1000
- 0s - loss: 1.8033 - acc: 0.6087
Epoch 896/1000
- 0s - loss: 1.8028 - acc: 0.5652
Epoch 897/1000
- 0s - loss: 1.8021 - acc: 0.6087
Epoch 898/1000
- 0s - loss: 1.8022 - acc: 0.5652
Epoch 899/1000
- 0s - loss: 1.8022 - acc: 0.5652
Epoch 900/1000
- 0s - loss: 1.8014 - acc: 0.5652
Epoch 901/1000
- 0s - loss: 1.8007 - acc: 0.5652
Epoch 902/1000
- 0s - loss: 1.7994 - acc: 0.5652
Epoch 903/1000
- 0s - loss: 1.7994 - acc: 0.5652
Epoch 904/1000
- 0s - loss: 1.7984 - acc: 0.6087
Epoch 905/1000
- 0s - loss: 1.7982 - acc: 0.6522
Epoch 906/1000
- 0s - loss: 1.7973 - acc: 0.6087
Epoch 907/1000
- 0s - loss: 1.7978 - acc: 0.6087
Epoch 908/1000
- 0s - loss: 1.7968 - acc: 0.6087
Epoch 909/1000
- 0s - loss: 1.7964 - acc: 0.6087
Epoch 910/1000
- 0s - loss: 1.7956 - acc: 0.5652
Epoch 911/1000
- 0s - loss: 1.7947 - acc: 0.5652
Epoch 912/1000
- 0s - loss: 1.7943 - acc: 0.6087
Epoch 913/1000
- 0s - loss: 1.7944 - acc: 0.6087
Epoch 914/1000
- 0s - loss: 1.7934 - acc: 0.5652
Epoch 915/1000
- 0s - loss: 1.7927 - acc: 0.6087
Epoch 916/1000
- 0s - loss: 1.7922 - acc: 0.6087
Epoch 917/1000
- 0s - loss: 1.7919 - acc: 0.6087
Epoch 918/1000
- 0s - loss: 1.7909 - acc: 0.6087
Epoch 919/1000
- 0s - loss: 1.7913 - acc: 0.5217
Epoch 920/1000
- 0s - loss: 1.7903 - acc: 0.6087
Epoch 921/1000
- 0s - loss: 1.7897 - acc: 0.6087
Epoch 922/1000
- 0s - loss: 1.7886 - acc: 0.6087
Epoch 923/1000
- 0s - loss: 1.7891 - acc: 0.6087
Epoch 924/1000
- 0s - loss: 1.7870 - acc: 0.6522
Epoch 925/1000
- 0s - loss: 1.7870 - acc: 0.6522
Epoch 926/1000
- 0s - loss: 1.7861 - acc: 0.6522
Epoch 927/1000
- 0s - loss: 1.7861 - acc: 0.6957
Epoch 928/1000
- 0s - loss: 1.7856 - acc: 0.6957
Epoch 929/1000
- 0s - loss: 1.7852 - acc: 0.6522
Epoch 930/1000
- 0s - loss: 1.7856 - acc: 0.6522
Epoch 931/1000
- 0s - loss: 1.7840 - acc: 0.6522
Epoch 932/1000
- 0s - loss: 1.7840 - acc: 0.6957
Epoch 933/1000
- 0s - loss: 1.7834 - acc: 0.6957
Epoch 934/1000
- 0s - loss: 1.7832 - acc: 0.6522
Epoch 935/1000
- 0s - loss: 1.7822 - acc: 0.6957
Epoch 936/1000
- 0s - loss: 1.7821 - acc: 0.6522
Epoch 937/1000
- 0s - loss: 1.7808 - acc: 0.6522
Epoch 938/1000
- 0s - loss: 1.7805 - acc: 0.6522
Epoch 939/1000
- 0s - loss: 1.7796 - acc: 0.7391
Epoch 940/1000
- 0s - loss: 1.7790 - acc: 0.7391
Epoch 941/1000
- 0s - loss: 1.7787 - acc: 0.6522
Epoch 942/1000
- 0s - loss: 1.7784 - acc: 0.7391
Epoch 943/1000
- 0s - loss: 1.7779 - acc: 0.6957
Epoch 944/1000
- 0s - loss: 1.7772 - acc: 0.6957
Epoch 945/1000
- 0s - loss: 1.7769 - acc: 0.6957
Epoch 946/1000
- 0s - loss: 1.7760 - acc: 0.6522
Epoch 947/1000
- 0s - loss: 1.7766 - acc: 0.6957
Epoch 948/1000
- 0s - loss: 1.7749 - acc: 0.6522
Epoch 949/1000
- 0s - loss: 1.7745 - acc: 0.6522
Epoch 950/1000
- 0s - loss: 1.7748 - acc: 0.6957
Epoch 951/1000
- 0s - loss: 1.7730 - acc: 0.6522
Epoch 952/1000
- 0s - loss: 1.7734 - acc: 0.5652
Epoch 953/1000
- 0s - loss: 1.7725 - acc: 0.6087
Epoch 954/1000
- 0s - loss: 1.7718 - acc: 0.6087
Epoch 955/1000
- 0s - loss: 1.7728 - acc: 0.6087
Epoch 956/1000
- 0s - loss: 1.7713 - acc: 0.6087
Epoch 957/1000
- 0s - loss: 1.7707 - acc: 0.5652
Epoch 958/1000
- 0s - loss: 1.7706 - acc: 0.6087
Epoch 959/1000
- 0s - loss: 1.7696 - acc: 0.6522
Epoch 960/1000
- 0s - loss: 1.7690 - acc: 0.6087
Epoch 961/1000
- 0s - loss: 1.7688 - acc: 0.5652
Epoch 962/1000
- 0s - loss: 1.7673 - acc: 0.6522
Epoch 963/1000
- 0s - loss: 1.7678 - acc: 0.6087
Epoch 964/1000
- 0s - loss: 1.7671 - acc: 0.6087
Epoch 965/1000
- 0s - loss: 1.7667 - acc: 0.5652
Epoch 966/1000
- 0s - loss: 1.7664 - acc: 0.5217
Epoch 967/1000
- 0s - loss: 1.7659 - acc: 0.5652
Epoch 968/1000
- 0s - loss: 1.7644 - acc: 0.6087
Epoch 969/1000
- 0s - loss: 1.7646 - acc: 0.6087
Epoch 970/1000
- 0s - loss: 1.7644 - acc: 0.6087
Epoch 971/1000
- 0s - loss: 1.7636 - acc: 0.6522
Epoch 972/1000
- 0s - loss: 1.7639 - acc: 0.6522
Epoch 973/1000
- 0s - loss: 1.7617 - acc: 0.6957
Epoch 974/1000
- 0s - loss: 1.7617 - acc: 0.6522
Epoch 975/1000
- 0s - loss: 1.7611 - acc: 0.6087
Epoch 976/1000
- 0s - loss: 1.7614 - acc: 0.6087
Epoch 977/1000
- 0s - loss: 1.7602 - acc: 0.6957
Epoch 978/1000
- 0s - loss: 1.7605 - acc: 0.6957
Epoch 979/1000
- 0s - loss: 1.7598 - acc: 0.6522
Epoch 980/1000
- 0s - loss: 1.7588 - acc: 0.6522
Epoch 981/1000
- 0s - loss: 1.7583 - acc: 0.6522
Epoch 982/1000
- 0s - loss: 1.7577 - acc: 0.6522
Epoch 983/1000
- 0s - loss: 1.7579 - acc: 0.6087
Epoch 984/1000
- 0s - loss: 1.7574 - acc: 0.6087
Epoch 985/1000
- 0s - loss: 1.7561 - acc: 0.6522
Epoch 986/1000
- 0s - loss: 1.7561 - acc: 0.6522
Epoch 987/1000
- 0s - loss: 1.7550 - acc: 0.6087
Epoch 988/1000
- 0s - loss: 1.7547 - acc: 0.5652
Epoch 989/1000
- 0s - loss: 1.7539 - acc: 0.6087
Epoch 990/1000
- 0s - loss: 1.7542 - acc: 0.6087
Epoch 991/1000
- 0s - loss: 1.7530 - acc: 0.6522
Epoch 992/1000
- 0s - loss: 1.7538 - acc: 0.6087
Epoch 993/1000
- 0s - loss: 1.7528 - acc: 0.6087
Epoch 994/1000
- 0s - loss: 1.7521 - acc: 0.6087
Epoch 995/1000
- 0s - loss: 1.7516 - acc: 0.6522
Epoch 996/1000
- 0s - loss: 1.7516 - acc: 0.6522
Epoch 997/1000
- 0s - loss: 1.7500 - acc: 0.6957
Epoch 998/1000
- 0s - loss: 1.7493 - acc: 0.6522
Epoch 999/1000
- 0s - loss: 1.7490 - acc: 0.6957
Epoch 1000/1000
- 0s - loss: 1.7488 - acc: 0.6522
23/23 [==============================] - 0s 9ms/step
Model Accuracy: 0.70
['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> L
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> Q
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> T
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> V
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> X
['U', 'V', 'W'] -> Z
['V', 'W', 'X'] -> Z
['W', 'X', 'Y'] -> Z
X.shape[1], y.shape[1] # get a sense of the shapes to understand the network architecture
The network does learn, and could be trained to get a good accuracy. But what's really going on here?
Let's leave aside for a moment the simplistic training data (one fun experiment would be to create corrupted sequences and augment the data with those, forcing the network to pay attention to the whole sequence).
Because the model is fundamentally symmetric and stateless (in terms of the sequence; naturally it has weights), this model would need to learn every sequential feature relative to every single sequence position. That seems difficult, inflexible, and inefficient.
Maybe we could add layers, neurons, and extra connections to mitigate parts of the problem. We could also do things like a 1D convolution to pick up frequencies and some patterns.
But instead, it might make more sense to explicitly model the sequential nature of the data (a bit like how we explictly modeled the 2D nature of image data with CNNs).
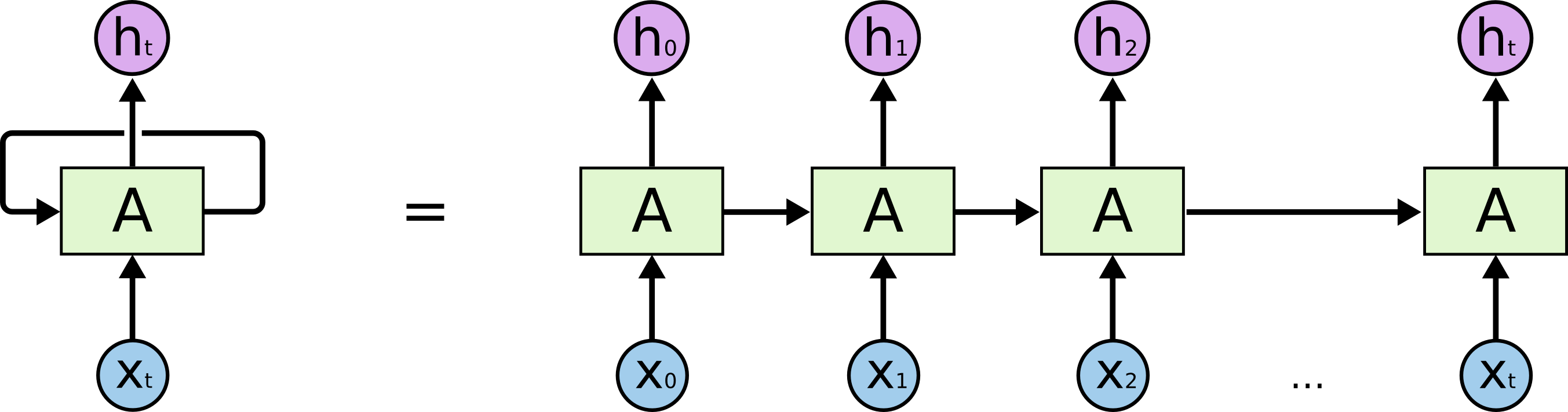
Recurrent Neural Network Concept
Let's take the neuron's output from one time (t) and feed it into that same neuron at a later time (t+1), in combination with other relevant inputs. Then we would have a neuron with memory.
We can weight the "return" of that value and train the weight -- so the neuron learns how important the previous value is relative to the current one.
Different neurons might learn to "remember" different amounts of prior history.
This concept is called a Recurrent Neural Network, originally developed around the 1980s.
Let's recall some pointers from the crash intro to Deep learning.
Watch following videos now for 12 minutes for the fastest introduction to RNNs and LSTMs
Udacity: Deep Learning by Vincent Vanhoucke - Recurrent Neural network
Recurrent neural network
 http://colah.github.io/posts/2015-08-Understanding-LSTMs/
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
http://karpathy.github.io/2015/05/21/rnn-effectiveness/ ***
LSTM - Long short term memory
GRU - Gated recurrent unit
 http://arxiv.org/pdf/1406.1078v3.pdf
http://arxiv.org/pdf/1406.1078v3.pdf
Training a Recurrent Neural Network

We can train an RNN using backpropagation with a minor twist: since RNN neurons with different states over time can be "unrolled" (i.e., are analogous) to a sequence of neurons with the "remember" weight linking directly forward from (t) to (t+1), we can backpropagate through time as well as the physical layers of the network.
This is, in fact, called Backpropagation Through Time (BPTT)
The idea is sound but -- since it creates patterns similar to very deep networks -- it suffers from the same challenges: * Vanishing gradient * Exploding gradient * Saturation * etc.
i.e., many of the same problems with early deep feed-forward networks having lots of weights.
10 steps back in time for a single layer is a not as bad as 10 layers (since there are fewer connections and, hence, weights) but it does get expensive.
ASIDE: Hierarchical and Recursive Networks, Bidirectional RNN
Network topologies can be built to reflect the relative structure of the data we are modeling. E.g., for natural language, grammar constraints mean that both hierarchy and (limited) recursion may allow a physically smaller model to achieve more effective capacity.
A bi-directional RNN includes values from previous and subsequent time steps. This is less strange than it sounds at first: after all, in many problems, such as sentence translation (where BiRNNs are very popular) we usually have the entire source sequence at one time. In that case, a BiDiRNN is really just saying that both prior and subsequent words can influence the interpretation of each word, something we humans take for granted.
Recent versions of neural net libraries have support for bidirectional networks, although you may need to write (or locate) a little code yourself if you want to experiment with hierarchical networks.
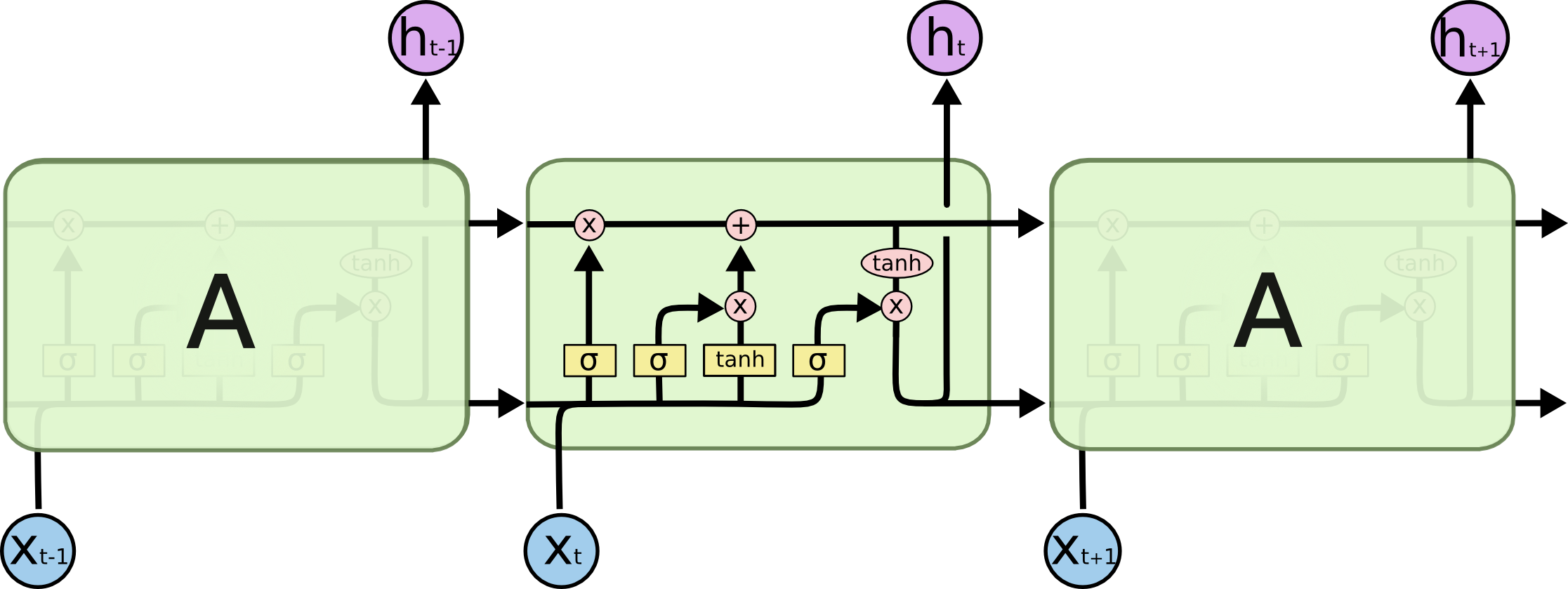
Long Short-Term Memory (LSTM)
"Pure" RNNs were never very successful. Sepp Hochreiter and Jürgen Schmidhuber (1997) made a game-changing contribution with the publication of the Long Short-Term Memory unit. How game changing? It's effectively state of the art today.
(Credit and much thanks to Chris Olah, http://colah.github.io/about.html, Research Scientist at Google Brain, for publishing the following excellent diagrams!)
*In the following diagrams, pay close attention that the output value is "split" for graphical purposes -- so the two *h* arrows/signals coming out are the same signal.*
RNN Cell: 
LSTM Cell:

An LSTM unit is a neuron with some bonus features: * Cell state propagated across time * Input, Output, Forget gates * Learns retention/discard of cell state * Admixture of new data * Output partly distinct from state * Use of addition (not multiplication) to combine input and cell state allows state to propagate unimpeded across time (addition of gradient)
ASIDE: Variations on LSTM
... include "peephole" where gate functions have direct access to cell state; convolutional; and bidirectional, where we can "cheat" by letting neurons learn from future time steps and not just previous time steps.
Slow down ... exactly what's getting added to where? For a step-by-step walk through, read Chris Olah's full post http://colah.github.io/posts/2015-08-Understanding-LSTMs/
Do LSTMs Work Reasonably Well?
Yes! These architectures are in production (2017) for deep-learning-enabled products at Baidu, Google, Microsoft, Apple, and elsewhere. They are used to solve problems in time series analysis, speech recognition and generation, connected handwriting, grammar, music, and robot control systems.
Let's Code an LSTM Variant of our Sequence Lab
(this great demo example courtesy of Jason Brownlee: http://machinelearningmastery.com/understanding-stateful-lstm-recurrent-neural-networks-python-keras/)
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.utils import np_utils
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print (seq_in, '->', seq_out)
# reshape X to be .......[samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))
X = X / float(len(alphabet))
y = np_utils.to_categorical(dataY)
# Let’s define an LSTM network with 32 units and an output layer with a softmax activation function for making predictions.
# a naive implementation of LSTM
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2]))) # <- LSTM layer...
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=400, batch_size=1, verbose=2)
scores = model.evaluate(X, y)
print("Model Accuracy: %.2f%%" % (scores[1]*100))
for pattern in dataX:
x = numpy.reshape(pattern, (1, len(pattern), 1))
x = x / float(len(alphabet))
prediction = model.predict(x, verbose=0)
index = numpy.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
print (seq_in, "->", result)
ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z
Epoch 1/400
- 4s - loss: 3.2653 - acc: 0.0000e+00
Epoch 2/400
- 0s - loss: 3.2498 - acc: 0.0000e+00
Epoch 3/400
- 0s - loss: 3.2411 - acc: 0.0000e+00
Epoch 4/400
- 0s - loss: 3.2330 - acc: 0.0435
Epoch 5/400
- 0s - loss: 3.2242 - acc: 0.0435
Epoch 6/400
- 0s - loss: 3.2152 - acc: 0.0435
Epoch 7/400
- 0s - loss: 3.2046 - acc: 0.0435
Epoch 8/400
- 0s - loss: 3.1946 - acc: 0.0435
Epoch 9/400
- 0s - loss: 3.1835 - acc: 0.0435
Epoch 10/400
- 0s - loss: 3.1720 - acc: 0.0435
Epoch 11/400
- 0s - loss: 3.1583 - acc: 0.0435
Epoch 12/400
- 0s - loss: 3.1464 - acc: 0.0435
Epoch 13/400
- 0s - loss: 3.1316 - acc: 0.0435
Epoch 14/400
- 0s - loss: 3.1176 - acc: 0.0435
Epoch 15/400
- 0s - loss: 3.1036 - acc: 0.0435
Epoch 16/400
- 0s - loss: 3.0906 - acc: 0.0435
Epoch 17/400
- 0s - loss: 3.0775 - acc: 0.0435
Epoch 18/400
- 0s - loss: 3.0652 - acc: 0.0435
Epoch 19/400
- 0s - loss: 3.0515 - acc: 0.0435
Epoch 20/400
- 0s - loss: 3.0388 - acc: 0.0435
Epoch 21/400
- 0s - loss: 3.0213 - acc: 0.0435
Epoch 22/400
- 0s - loss: 3.0044 - acc: 0.0435
Epoch 23/400
- 0s - loss: 2.9900 - acc: 0.1304
Epoch 24/400
- 0s - loss: 2.9682 - acc: 0.0870
Epoch 25/400
- 0s - loss: 2.9448 - acc: 0.0870
Epoch 26/400
- 0s - loss: 2.9237 - acc: 0.0870
Epoch 27/400
- 0s - loss: 2.8948 - acc: 0.0870
Epoch 28/400
- 0s - loss: 2.8681 - acc: 0.0870
Epoch 29/400
- 0s - loss: 2.8377 - acc: 0.0435
Epoch 30/400
- 0s - loss: 2.8008 - acc: 0.0870
Epoch 31/400
- 0s - loss: 2.7691 - acc: 0.0435
Epoch 32/400
- 0s - loss: 2.7268 - acc: 0.0870
Epoch 33/400
- 0s - loss: 2.6963 - acc: 0.0870
Epoch 34/400
- 0s - loss: 2.6602 - acc: 0.0870
Epoch 35/400
- 0s - loss: 2.6285 - acc: 0.1304
Epoch 36/400
- 0s - loss: 2.5979 - acc: 0.0870
Epoch 37/400
- 0s - loss: 2.5701 - acc: 0.1304
Epoch 38/400
- 0s - loss: 2.5443 - acc: 0.0870
Epoch 39/400
- 0s - loss: 2.5176 - acc: 0.0870
Epoch 40/400
- 0s - loss: 2.4962 - acc: 0.0870
Epoch 41/400
- 0s - loss: 2.4737 - acc: 0.0870
Epoch 42/400
- 0s - loss: 2.4496 - acc: 0.1739
Epoch 43/400
- 0s - loss: 2.4295 - acc: 0.1304
Epoch 44/400
- 0s - loss: 2.4045 - acc: 0.1739
Epoch 45/400
- 0s - loss: 2.3876 - acc: 0.1739
Epoch 46/400
- 0s - loss: 2.3671 - acc: 0.1739
Epoch 47/400
- 0s - loss: 2.3512 - acc: 0.1739
Epoch 48/400
- 0s - loss: 2.3301 - acc: 0.1739
Epoch 49/400
- 0s - loss: 2.3083 - acc: 0.1739
Epoch 50/400
- 0s - loss: 2.2833 - acc: 0.1739
Epoch 51/400
- 0s - loss: 2.2715 - acc: 0.1739
Epoch 52/400
- 0s - loss: 2.2451 - acc: 0.2174
Epoch 53/400
- 0s - loss: 2.2219 - acc: 0.2174
Epoch 54/400
- 0s - loss: 2.2025 - acc: 0.1304
Epoch 55/400
- 0s - loss: 2.1868 - acc: 0.2174
Epoch 56/400
- 0s - loss: 2.1606 - acc: 0.2174
Epoch 57/400
- 0s - loss: 2.1392 - acc: 0.2609
Epoch 58/400
- 0s - loss: 2.1255 - acc: 0.1739
Epoch 59/400
- 0s - loss: 2.1084 - acc: 0.2609
Epoch 60/400
- 0s - loss: 2.0835 - acc: 0.2609
Epoch 61/400
- 0s - loss: 2.0728 - acc: 0.2609
Epoch 62/400
- 0s - loss: 2.0531 - acc: 0.2174
Epoch 63/400
- 0s - loss: 2.0257 - acc: 0.2174
Epoch 64/400
- 0s - loss: 2.0192 - acc: 0.2174
Epoch 65/400
- 0s - loss: 1.9978 - acc: 0.2609
Epoch 66/400
- 0s - loss: 1.9792 - acc: 0.1304
Epoch 67/400
- 0s - loss: 1.9655 - acc: 0.3478
Epoch 68/400
- 0s - loss: 1.9523 - acc: 0.2609
Epoch 69/400
- 0s - loss: 1.9402 - acc: 0.2609
Epoch 70/400
- 0s - loss: 1.9220 - acc: 0.3043
Epoch 71/400
- 0s - loss: 1.9075 - acc: 0.2609
Epoch 72/400
- 0s - loss: 1.8899 - acc: 0.3913
Epoch 73/400
- 0s - loss: 1.8829 - acc: 0.3043
Epoch 74/400
- 0s - loss: 1.8569 - acc: 0.2174
Epoch 75/400
- 0s - loss: 1.8435 - acc: 0.3043
Epoch 76/400
- 0s - loss: 1.8361 - acc: 0.3043
Epoch 77/400
- 0s - loss: 1.8228 - acc: 0.3478
Epoch 78/400
- 0s - loss: 1.8145 - acc: 0.3043
Epoch 79/400
- 0s - loss: 1.7982 - acc: 0.3913
Epoch 80/400
- 0s - loss: 1.7836 - acc: 0.3913
Epoch 81/400
- 0s - loss: 1.7795 - acc: 0.4348
Epoch 82/400
- 0s - loss: 1.7646 - acc: 0.4783
Epoch 83/400
- 0s - loss: 1.7487 - acc: 0.4348
Epoch 84/400
- 0s - loss: 1.7348 - acc: 0.4348
Epoch 85/400
- 0s - loss: 1.7249 - acc: 0.5217
Epoch 86/400
- 0s - loss: 1.7153 - acc: 0.4348
Epoch 87/400
- 0s - loss: 1.7095 - acc: 0.4348
Epoch 88/400
- 0s - loss: 1.6938 - acc: 0.4348
Epoch 89/400
- 0s - loss: 1.6849 - acc: 0.5217
Epoch 90/400
- 0s - loss: 1.6712 - acc: 0.4348
Epoch 91/400
- 0s - loss: 1.6617 - acc: 0.5652
Epoch 92/400
- 0s - loss: 1.6531 - acc: 0.4348
Epoch 93/400
- 0s - loss: 1.6459 - acc: 0.5217
Epoch 94/400
- 0s - loss: 1.6341 - acc: 0.4783
Epoch 95/400
- 0s - loss: 1.6289 - acc: 0.5652
Epoch 96/400
- 0s - loss: 1.6138 - acc: 0.4783
Epoch 97/400
- 0s - loss: 1.6042 - acc: 0.4348
Epoch 98/400
- 0s - loss: 1.5907 - acc: 0.5652
Epoch 99/400
- 0s - loss: 1.5868 - acc: 0.4783
Epoch 100/400
- 0s - loss: 1.5756 - acc: 0.5217
Epoch 101/400
- 0s - loss: 1.5681 - acc: 0.5652
Epoch 102/400
- 0s - loss: 1.5582 - acc: 0.5652
Epoch 103/400
- 0s - loss: 1.5478 - acc: 0.6087
Epoch 104/400
- 0s - loss: 1.5375 - acc: 0.6087
Epoch 105/400
- 0s - loss: 1.5340 - acc: 0.6522
Epoch 106/400
- 0s - loss: 1.5175 - acc: 0.6522
Epoch 107/400
- 0s - loss: 1.5127 - acc: 0.5652
Epoch 108/400
- 0s - loss: 1.5207 - acc: 0.5652
Epoch 109/400
- 0s - loss: 1.5064 - acc: 0.5652
Epoch 110/400
- 0s - loss: 1.4968 - acc: 0.5652
Epoch 111/400
- 0s - loss: 1.4843 - acc: 0.6522
Epoch 112/400
- 0s - loss: 1.4806 - acc: 0.5217
Epoch 113/400
- 0s - loss: 1.4702 - acc: 0.7826
Epoch 114/400
- 0s - loss: 1.4555 - acc: 0.6957
Epoch 115/400
- 0s - loss: 1.4459 - acc: 0.6087
Epoch 116/400
- 0s - loss: 1.4542 - acc: 0.6522
Epoch 117/400
- 0s - loss: 1.4375 - acc: 0.7391
Epoch 118/400
- 0s - loss: 1.4328 - acc: 0.7391
Epoch 119/400
- 0s - loss: 1.4338 - acc: 0.7826
Epoch 120/400
- 0s - loss: 1.4155 - acc: 0.6087
Epoch 121/400
- 0s - loss: 1.4043 - acc: 0.6957
Epoch 122/400
- 0s - loss: 1.4009 - acc: 0.7391
Epoch 123/400
- 0s - loss: 1.3980 - acc: 0.7391
Epoch 124/400
- 0s - loss: 1.3869 - acc: 0.6957
Epoch 125/400
- 0s - loss: 1.3837 - acc: 0.6522
Epoch 126/400
- 0s - loss: 1.3753 - acc: 0.7826
Epoch 127/400
- 0s - loss: 1.3670 - acc: 0.7391
Epoch 128/400
- 0s - loss: 1.3586 - acc: 0.7826
Epoch 129/400
- 0s - loss: 1.3564 - acc: 0.6957
Epoch 130/400
- 0s - loss: 1.3448 - acc: 0.6957
Epoch 131/400
- 0s - loss: 1.3371 - acc: 0.8261
Epoch 132/400
- 0s - loss: 1.3330 - acc: 0.6957
Epoch 133/400
- 0s - loss: 1.3353 - acc: 0.6957
Epoch 134/400
- 0s - loss: 1.3239 - acc: 0.7391
Epoch 135/400
- 0s - loss: 1.3152 - acc: 0.8696
Epoch 136/400
- 0s - loss: 1.3186 - acc: 0.7391
Epoch 137/400
- 0s - loss: 1.3026 - acc: 0.8261
Epoch 138/400
- 0s - loss: 1.2946 - acc: 0.8696
Epoch 139/400
- 0s - loss: 1.2903 - acc: 0.7826
Epoch 140/400
- 0s - loss: 1.2894 - acc: 0.7391
Epoch 141/400
- 0s - loss: 1.2887 - acc: 0.7826
Epoch 142/400
- 0s - loss: 1.2733 - acc: 0.7826
Epoch 143/400
- 0s - loss: 1.2709 - acc: 0.7826
Epoch 144/400
- 0s - loss: 1.2638 - acc: 0.7826
Epoch 145/400
- 0s - loss: 1.2636 - acc: 0.8261
Epoch 146/400
- 0s - loss: 1.2513 - acc: 0.8261
Epoch 147/400
- 0s - loss: 1.2459 - acc: 0.7826
Epoch 148/400
- 0s - loss: 1.2422 - acc: 0.8696
Epoch 149/400
- 0s - loss: 1.2354 - acc: 0.8696
Epoch 150/400
- 0s - loss: 1.2265 - acc: 0.7826
Epoch 151/400
- 0s - loss: 1.2295 - acc: 0.8696
Epoch 152/400
- 0s - loss: 1.2192 - acc: 0.8696
Epoch 153/400
- 0s - loss: 1.2146 - acc: 0.8261
Epoch 154/400
- 0s - loss: 1.2152 - acc: 0.7826
Epoch 155/400
- 0s - loss: 1.2052 - acc: 0.7826
Epoch 156/400
- 0s - loss: 1.1943 - acc: 0.9565
Epoch 157/400
- 0s - loss: 1.1902 - acc: 0.8696
Epoch 158/400
- 0s - loss: 1.1877 - acc: 0.8696
Epoch 159/400
- 0s - loss: 1.1822 - acc: 0.8696
Epoch 160/400
- 0s - loss: 1.1718 - acc: 0.8261
Epoch 161/400
- 0s - loss: 1.1740 - acc: 0.8696
Epoch 162/400
- 0s - loss: 1.1696 - acc: 0.8696
Epoch 163/400
- 0s - loss: 1.1593 - acc: 0.8261
Epoch 164/400
- 0s - loss: 1.1580 - acc: 0.8696
Epoch 165/400
- 0s - loss: 1.1519 - acc: 0.9130
Epoch 166/400
- 0s - loss: 1.1453 - acc: 0.8696
Epoch 167/400
- 0s - loss: 1.1479 - acc: 0.7826
Epoch 168/400
- 0s - loss: 1.1391 - acc: 0.7826
Epoch 169/400
- 0s - loss: 1.1348 - acc: 0.8261
Epoch 170/400
- 0s - loss: 1.1261 - acc: 0.8696
Epoch 171/400
- 0s - loss: 1.1268 - acc: 0.8261
Epoch 172/400
- 0s - loss: 1.1216 - acc: 0.7826
Epoch 173/400
- 0s - loss: 1.1119 - acc: 0.9130
Epoch 174/400
- 0s - loss: 1.1071 - acc: 0.9130
Epoch 175/400
- 0s - loss: 1.0984 - acc: 0.9130
Epoch 176/400
- 0s - loss: 1.0921 - acc: 0.9565
Epoch 177/400
- 0s - loss: 1.0938 - acc: 0.8696
Epoch 178/400
- 0s - loss: 1.0904 - acc: 0.8261
Epoch 179/400
- 0s - loss: 1.0905 - acc: 0.8696
Epoch 180/400
- 0s - loss: 1.0749 - acc: 0.9565
Epoch 181/400
- 0s - loss: 1.0749 - acc: 0.8261
Epoch 182/400
- 0s - loss: 1.0705 - acc: 0.9130
Epoch 183/400
- 0s - loss: 1.0686 - acc: 0.8696
Epoch 184/400
- 0s - loss: 1.0553 - acc: 0.9130
Epoch 185/400
- 0s - loss: 1.0552 - acc: 0.8696
Epoch 186/400
- 0s - loss: 1.0593 - acc: 0.9130
Epoch 187/400
- 0s - loss: 1.0508 - acc: 0.8261
Epoch 188/400
- 0s - loss: 1.0453 - acc: 0.8696
Epoch 189/400
- 0s - loss: 1.0394 - acc: 0.9565
Epoch 190/400
- 0s - loss: 1.0272 - acc: 0.9130
Epoch 191/400
- 0s - loss: 1.0385 - acc: 0.9130
Epoch 192/400
- 0s - loss: 1.0257 - acc: 0.8696
Epoch 193/400
- 0s - loss: 1.0218 - acc: 0.8696
Epoch 194/400
- 0s - loss: 1.0193 - acc: 0.9565
Epoch 195/400
- 0s - loss: 1.0195 - acc: 0.9130
Epoch 196/400
- 0s - loss: 1.0137 - acc: 0.9130
Epoch 197/400
- 0s - loss: 1.0050 - acc: 0.8696
Epoch 198/400
- 0s - loss: 0.9985 - acc: 0.9130
Epoch 199/400
- 0s - loss: 1.0016 - acc: 0.9565
Epoch 200/400
- 0s - loss: 0.9917 - acc: 0.8696
Epoch 201/400
- 0s - loss: 0.9952 - acc: 0.9130
Epoch 202/400
- 0s - loss: 0.9823 - acc: 0.9130
Epoch 203/400
- 0s - loss: 0.9765 - acc: 0.9565
Epoch 204/400
- 0s - loss: 0.9722 - acc: 0.9565
Epoch 205/400
- 0s - loss: 0.9756 - acc: 0.9130
Epoch 206/400
- 0s - loss: 0.9733 - acc: 0.9130
Epoch 207/400
- 0s - loss: 0.9768 - acc: 0.8261
Epoch 208/400
- 0s - loss: 0.9611 - acc: 0.9565
Epoch 209/400
- 0s - loss: 0.9548 - acc: 0.9565
Epoch 210/400
- 0s - loss: 0.9530 - acc: 0.8696
Epoch 211/400
- 0s - loss: 0.9481 - acc: 0.8696
Epoch 212/400
- 0s - loss: 0.9436 - acc: 0.9130
Epoch 213/400
- 0s - loss: 0.9435 - acc: 0.8696
Epoch 214/400
- 0s - loss: 0.9430 - acc: 0.9130
Epoch 215/400
- 0s - loss: 0.9281 - acc: 0.9130
Epoch 216/400
- 0s - loss: 0.9267 - acc: 0.9565
Epoch 217/400
- 0s - loss: 0.9263 - acc: 0.9130
Epoch 218/400
- 0s - loss: 0.9180 - acc: 0.9565
Epoch 219/400
- 0s - loss: 0.9151 - acc: 0.9565
Epoch 220/400
- 0s - loss: 0.9125 - acc: 0.9130
Epoch 221/400
- 0s - loss: 0.9090 - acc: 0.8696
Epoch 222/400
- 0s - loss: 0.9039 - acc: 0.9565
Epoch 223/400
- 0s - loss: 0.9032 - acc: 0.9565
Epoch 224/400
- 0s - loss: 0.8966 - acc: 0.9130
Epoch 225/400
- 0s - loss: 0.8935 - acc: 0.9130
Epoch 226/400
- 0s - loss: 0.8946 - acc: 0.9130
Epoch 227/400
- 0s - loss: 0.8875 - acc: 0.9130
Epoch 228/400
- 0s - loss: 0.8872 - acc: 0.9565
Epoch 229/400
- 0s - loss: 0.8758 - acc: 0.9130
Epoch 230/400
- 0s - loss: 0.8746 - acc: 0.9565
Epoch 231/400
- 0s - loss: 0.8720 - acc: 0.9565
Epoch 232/400
- 0s - loss: 0.8724 - acc: 0.9130
Epoch 233/400
- 0s - loss: 0.8626 - acc: 0.9130
Epoch 234/400
- 0s - loss: 0.8615 - acc: 0.9130
Epoch 235/400
- 0s - loss: 0.8623 - acc: 0.9130
Epoch 236/400
- 0s - loss: 0.8575 - acc: 0.9565
Epoch 237/400
- 0s - loss: 0.8543 - acc: 0.9565
Epoch 238/400
- 0s - loss: 0.8498 - acc: 0.9565
Epoch 239/400
- 0s - loss: 0.8391 - acc: 0.9565
Epoch 240/400
- 0s - loss: 0.8426 - acc: 0.9130
Epoch 241/400
- 0s - loss: 0.8361 - acc: 0.8696
Epoch 242/400
- 0s - loss: 0.8354 - acc: 0.9130
Epoch 243/400
- 0s - loss: 0.8280 - acc: 0.9565
Epoch 244/400
- 0s - loss: 0.8233 - acc: 0.9130
Epoch 245/400
- 0s - loss: 0.8176 - acc: 0.9130
Epoch 246/400
- 0s - loss: 0.8149 - acc: 0.9565
Epoch 247/400
- 0s - loss: 0.8064 - acc: 0.9565
Epoch 248/400
- 0s - loss: 0.8156 - acc: 0.9565
Epoch 249/400
- 0s - loss: 0.8049 - acc: 0.9565
Epoch 250/400
- 0s - loss: 0.8014 - acc: 0.9565
Epoch 251/400
- 0s - loss: 0.7945 - acc: 0.9565
Epoch 252/400
- 0s - loss: 0.7918 - acc: 0.9565
Epoch 253/400
- 0s - loss: 0.7897 - acc: 0.9565
Epoch 254/400
- 0s - loss: 0.7859 - acc: 0.9565
Epoch 255/400
- 0s - loss: 0.7810 - acc: 0.9565
Epoch 256/400
- 0s - loss: 0.7760 - acc: 0.9565
Epoch 257/400
- 0s - loss: 0.7822 - acc: 0.9130
Epoch 258/400
- 0s - loss: 0.7783 - acc: 0.9565
Epoch 259/400
- 0s - loss: 0.7672 - acc: 0.9565
Epoch 260/400
- 0s - loss: 0.7705 - acc: 0.9565
Epoch 261/400
- 0s - loss: 0.7659 - acc: 0.9565
Epoch 262/400
- 0s - loss: 0.7604 - acc: 0.9565
Epoch 263/400
- 0s - loss: 0.7585 - acc: 0.9565
Epoch 264/400
- 0s - loss: 0.7564 - acc: 0.9565
Epoch 265/400
- 0s - loss: 0.7527 - acc: 0.9565
Epoch 266/400
- 0s - loss: 0.7418 - acc: 0.9565
Epoch 267/400
- 0s - loss: 0.7425 - acc: 0.9565
Epoch 268/400
- 0s - loss: 0.7351 - acc: 0.9565
Epoch 269/400
- 0s - loss: 0.7425 - acc: 0.9565
Epoch 270/400
- 0s - loss: 0.7334 - acc: 0.9565
Epoch 271/400
- 0s - loss: 0.7315 - acc: 0.9565
Epoch 272/400
- 0s - loss: 0.7305 - acc: 0.9565
Epoch 273/400
- 0s - loss: 0.7183 - acc: 0.9565
Epoch 274/400
- 0s - loss: 0.7198 - acc: 0.9565
Epoch 275/400
- 0s - loss: 0.7197 - acc: 1.0000
Epoch 276/400
- 0s - loss: 0.7125 - acc: 0.9565
Epoch 277/400
- 0s - loss: 0.7105 - acc: 1.0000
Epoch 278/400
- 0s - loss: 0.7074 - acc: 0.9565
Epoch 279/400
- 0s - loss: 0.7033 - acc: 0.9565
Epoch 280/400
- 0s - loss: 0.6993 - acc: 0.9565
Epoch 281/400
- 0s - loss: 0.6954 - acc: 0.9565
Epoch 282/400
- 0s - loss: 0.6952 - acc: 0.9565
Epoch 283/400
- 0s - loss: 0.6964 - acc: 0.9565
Epoch 284/400
- 0s - loss: 0.6862 - acc: 0.9565
Epoch 285/400
- 0s - loss: 0.6928 - acc: 0.9565
Epoch 286/400
- 0s - loss: 0.6861 - acc: 0.9565
Epoch 287/400
- 0s - loss: 0.6760 - acc: 0.9565
Epoch 288/400
- 0s - loss: 0.6756 - acc: 0.9565
Epoch 289/400
- 0s - loss: 0.6821 - acc: 0.9565
Epoch 290/400
- 0s - loss: 0.6716 - acc: 0.9565
Epoch 291/400
- 0s - loss: 0.6671 - acc: 0.9565
Epoch 292/400
- 0s - loss: 0.6652 - acc: 0.9565
Epoch 293/400
- 0s - loss: 0.6594 - acc: 1.0000
Epoch 294/400
- 0s - loss: 0.6568 - acc: 1.0000
Epoch 295/400
- 0s - loss: 0.6503 - acc: 1.0000
Epoch 296/400
- 0s - loss: 0.6498 - acc: 1.0000
Epoch 297/400
- 0s - loss: 0.6441 - acc: 0.9565
Epoch 298/400
- 0s - loss: 0.6420 - acc: 0.9565
Epoch 299/400
- 0s - loss: 0.6418 - acc: 0.9565
Epoch 300/400
- 0s - loss: 0.6375 - acc: 0.9565
Epoch 301/400
- 0s - loss: 0.6368 - acc: 0.9565
Epoch 302/400
- 0s - loss: 0.6328 - acc: 0.9565
Epoch 303/400
- 0s - loss: 0.6341 - acc: 0.9565
Epoch 304/400
- 0s - loss: 0.6246 - acc: 0.9565
Epoch 305/400
- 0s - loss: 0.6265 - acc: 0.9565
Epoch 306/400
- 0s - loss: 0.6285 - acc: 0.9565
Epoch 307/400
- 0s - loss: 0.6145 - acc: 0.9565
Epoch 308/400
- 0s - loss: 0.6174 - acc: 0.9565
Epoch 309/400
- 0s - loss: 0.6137 - acc: 0.9565
Epoch 310/400
- 0s - loss: 0.6069 - acc: 0.9565
Epoch 311/400
- 0s - loss: 0.6028 - acc: 0.9565
Epoch 312/400
- 0s - loss: 0.6075 - acc: 0.9565
Epoch 313/400
- 0s - loss: 0.6018 - acc: 0.9565
Epoch 314/400
- 0s - loss: 0.5959 - acc: 1.0000
Epoch 315/400
- 0s - loss: 0.6004 - acc: 1.0000
Epoch 316/400
- 0s - loss: 0.6125 - acc: 0.9565
Epoch 317/400
- 0s - loss: 0.5984 - acc: 0.9565
Epoch 318/400
- 0s - loss: 0.5873 - acc: 1.0000
Epoch 319/400
- 0s - loss: 0.5860 - acc: 0.9565
Epoch 320/400
- 0s - loss: 0.5847 - acc: 1.0000
Epoch 321/400
- 0s - loss: 0.5752 - acc: 1.0000
Epoch 322/400
- 0s - loss: 0.5766 - acc: 0.9565
Epoch 323/400
- 0s - loss: 0.5750 - acc: 0.9565
Epoch 324/400
- 0s - loss: 0.5716 - acc: 0.9565
Epoch 325/400
- 0s - loss: 0.5647 - acc: 0.9565
Epoch 326/400
- 0s - loss: 0.5655 - acc: 1.0000
Epoch 327/400
- 0s - loss: 0.5665 - acc: 0.9565
Epoch 328/400
- 0s - loss: 0.5564 - acc: 0.9565
Epoch 329/400
- 0s - loss: 0.5576 - acc: 0.9565
Epoch 330/400
- 0s - loss: 0.5532 - acc: 0.9565
Epoch 331/400
- 0s - loss: 0.5512 - acc: 1.0000
Epoch 332/400
- 0s - loss: 0.5471 - acc: 1.0000
Epoch 333/400
- 0s - loss: 0.5410 - acc: 0.9565
Epoch 334/400
- 0s - loss: 0.5383 - acc: 0.9565
Epoch 335/400
- 0s - loss: 0.5384 - acc: 0.9565
Epoch 336/400
- 0s - loss: 0.5364 - acc: 1.0000
Epoch 337/400
- 0s - loss: 0.5335 - acc: 1.0000
Epoch 338/400
- 0s - loss: 0.5356 - acc: 1.0000
Epoch 339/400
- 0s - loss: 0.5265 - acc: 0.9565
Epoch 340/400
- 0s - loss: 0.5293 - acc: 1.0000
Epoch 341/400
- 0s - loss: 0.5185 - acc: 1.0000
Epoch 342/400
- 0s - loss: 0.5173 - acc: 1.0000
Epoch 343/400
- 0s - loss: 0.5162 - acc: 0.9565
Epoch 344/400
- 0s - loss: 0.5161 - acc: 0.9565
Epoch 345/400
- 0s - loss: 0.5190 - acc: 0.9565
Epoch 346/400
- 0s - loss: 0.5180 - acc: 1.0000
Epoch 347/400
- 0s - loss: 0.5265 - acc: 0.9565
Epoch 348/400
- 0s - loss: 0.5096 - acc: 1.0000
Epoch 349/400
- 0s - loss: 0.5038 - acc: 1.0000
Epoch 350/400
- 0s - loss: 0.4985 - acc: 0.9565
Epoch 351/400
- 0s - loss: 0.5008 - acc: 1.0000
Epoch 352/400
- 0s - loss: 0.4996 - acc: 1.0000
Epoch 353/400
- 0s - loss: 0.4922 - acc: 1.0000
Epoch 354/400
- 0s - loss: 0.4895 - acc: 0.9565
Epoch 355/400
- 0s - loss: 0.4833 - acc: 0.9565
Epoch 356/400
- 0s - loss: 0.4889 - acc: 1.0000
Epoch 357/400
- 0s - loss: 0.4822 - acc: 0.9565
Epoch 358/400
- 0s - loss: 0.4850 - acc: 0.9565
Epoch 359/400
- 0s - loss: 0.4770 - acc: 1.0000
Epoch 360/400
- 0s - loss: 0.4741 - acc: 1.0000
Epoch 361/400
- 0s - loss: 0.4734 - acc: 0.9565
Epoch 362/400
- 0s - loss: 0.4705 - acc: 0.9565
Epoch 363/400
- 0s - loss: 0.4677 - acc: 0.9565
Epoch 364/400
- 0s - loss: 0.4648 - acc: 1.0000
Epoch 365/400
- 0s - loss: 0.4643 - acc: 1.0000
Epoch 366/400
- 0s - loss: 0.4612 - acc: 0.9565
Epoch 367/400
- 0s - loss: 0.4572 - acc: 1.0000
Epoch 368/400
- 0s - loss: 0.4559 - acc: 1.0000
Epoch 369/400
- 0s - loss: 0.4512 - acc: 1.0000
Epoch 370/400
- 0s - loss: 0.4534 - acc: 1.0000
Epoch 371/400
- 0s - loss: 0.4496 - acc: 1.0000
Epoch 372/400
- 0s - loss: 0.4516 - acc: 0.9565
Epoch 373/400
- 0s - loss: 0.4449 - acc: 1.0000
Epoch 374/400
- 0s - loss: 0.4391 - acc: 1.0000
Epoch 375/400
- 0s - loss: 0.4428 - acc: 0.9565
Epoch 376/400
- 0s - loss: 0.4387 - acc: 0.9565
Epoch 377/400
- 0s - loss: 0.4451 - acc: 1.0000
Epoch 378/400
- 0s - loss: 0.4336 - acc: 1.0000
Epoch 379/400
- 0s - loss: 0.4297 - acc: 1.0000
Epoch 380/400
- 0s - loss: 0.4264 - acc: 0.9565
Epoch 381/400
- 0s - loss: 0.4266 - acc: 1.0000
Epoch 382/400
- 0s - loss: 0.4333 - acc: 0.9565
Epoch 383/400
- 0s - loss: 0.4325 - acc: 1.0000
Epoch 384/400
- 0s - loss: 0.4246 - acc: 1.0000
Epoch 385/400
- 0s - loss: 0.4169 - acc: 1.0000
Epoch 386/400
- 0s - loss: 0.4133 - acc: 1.0000
Epoch 387/400
- 0s - loss: 0.4156 - acc: 1.0000
Epoch 388/400
- 0s - loss: 0.4162 - acc: 1.0000
Epoch 389/400
- 0s - loss: 0.4086 - acc: 1.0000
Epoch 390/400
- 0s - loss: 0.4061 - acc: 1.0000
Epoch 391/400
- 0s - loss: 0.4045 - acc: 1.0000
Epoch 392/400
- 0s - loss: 0.4058 - acc: 0.9565
Epoch 393/400
- 0s - loss: 0.3974 - acc: 1.0000
Epoch 394/400
- 0s - loss: 0.3964 - acc: 1.0000
Epoch 395/400
- 0s - loss: 0.3930 - acc: 1.0000
Epoch 396/400
- 0s - loss: 0.3981 - acc: 1.0000
Epoch 397/400
- 0s - loss: 0.3871 - acc: 1.0000
Epoch 398/400
- 0s - loss: 0.3853 - acc: 1.0000
Epoch 399/400
- 0s - loss: 0.3805 - acc: 1.0000
Epoch 400/400
- 0s - loss: 0.3810 - acc: 1.0000
23/23 [==============================] - 1s 33ms/step
Model Accuracy: 100.00%
['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> M
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> P
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> S
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> U
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> W
['U', 'V', 'W'] -> X
['V', 'W', 'X'] -> Y
['W', 'X', 'Y'] -> Z
(X.shape[1], X.shape[2]) # the input shape to LSTM layer with 32 neurons is given by dimensions of time-steps and features
X.shape[0], y.shape[1] # number of examples and number of categorical outputs
Memory and context
If this network is learning the way we would like, it should be robust to noise and also understand the relative context (in this case, where a prior letter occurs in the sequence).
I.e., we should be able to give it corrupted sequences, and it should produce reasonably correct predictions.
Make the following change to the code to test this out:
You Try!
- We'll use "W" for our erroneous/corrupted data element
- Add code at the end to predict on the following sequences:
- 'WBC', 'WKL', 'WTU', 'DWF', 'MWO', 'VWW', 'GHW', 'JKW', 'PQW'
- Notice any pattern? Hard to tell from a small sample, but if you play with it (trying sequences from different places in the alphabet, or different "corruption" letters, you'll notice patterns that give a hint at what the network is learning
The solution is in 060_DLByABr_05a-LSTM-Solution if you are lazy right now or get stuck.
Pretty cool... BUT
This alphabet example does seem a bit like "tennis without the net" since the original goal was to develop networks that could extract patterns from complex, ambiguous content like natural language or music, and we've been playing with a sequence (Roman alphabet) that is 100% deterministic and tiny in size.
First, go ahead and start 061_DLByABr_05b-LSTM-Language since it will take several minutes to produce its first output.
This latter script is taken 100% exactly as-is from the Keras library examples folder (https://github.com/fchollet/keras/blob/master/examples/lstmtextgeneration.py) and uses precisely the logic we just learned, in order to learn and synthesize English language text from a single-author corpuse. The amazing thing is that the text is learned and generated one letter at a time, just like we did with the alphabet.
Compared to our earlier examples... * there is a minor difference in the way the inputs are encoded, using 1-hot vectors * and there is a significant difference in the way the outputs (predictions) are generated: instead of taking just the most likely output class (character) via argmax as we did before, this time we are treating the output as a distribution and sampling from the distribution.
Let's take a look at the code ... but even so, this will probably be something to come back to after fika or a long break, as the training takes about 5 minutes per epoch (late 2013 MBP CPU) and we need around 20 epochs (80 minutes!) to get good output.
import sys
sys.exit(0) #just to keep from accidentally running this code (that is already in 061_DLByABr_05b-LSTM-Language) HERE
'''Example script to generate text from Nietzsche's writings.
At least 20 epochs are required before the generated text
starts sounding coherent.
It is recommended to run this script on GPU, as recurrent
networks are quite computationally intensive.
If you try this script on new data, make sure your corpus
has at least ~100k characters. ~1M is better.
'''
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LSTM
from keras.optimizers import RMSprop
from keras.utils.data_utils import get_file
import numpy as np
import random
import sys
path = "../data/nietzsche.txt"
text = open(path).read().lower()
print('corpus length:', len(text))
chars = sorted(list(set(text)))
print('total chars:', len(chars))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
# cut the text in semi-redundant sequences of maxlen characters
maxlen = 40
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
print('nb sequences:', len(sentences))
print('Vectorization...')
X = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
# build the model: a single LSTM
print('Build model...')
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(chars))))
model.add(Dense(len(chars)))
model.add(Activation('softmax'))
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
def sample(preds, temperature=1.0):
# helper function to sample an index from a probability array
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / temperature
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)
# train the model, output generated text after each iteration
for iteration in range(1, 60):
print()
print('-' * 50)
print('Iteration', iteration)
model.fit(X, y, batch_size=128, epochs=1)
start_index = random.randint(0, len(text) - maxlen - 1)
for diversity in [0.2, 0.5, 1.0, 1.2]:
print()
print('----- diversity:', diversity)
generated = ''
sentence = text[start_index: start_index + maxlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(400):
x = np.zeros((1, maxlen, len(chars)))
for t, char in enumerate(sentence):
x[0, t, char_indices[char]] = 1.
preds = model.predict(x, verbose=0)[0]
next_index = sample(preds, diversity)
next_char = indices_char[next_index]
generated += next_char
sentence = sentence[1:] + next_char
sys.stdout.write(next_char)
sys.stdout.flush()
print()
/databricks/python/lib/python3.7/site-packages/IPython/core/interactiveshell.py:3304: UserWarning: To exit: use 'exit', 'quit', or Ctrl-D.
warn("To exit: use 'exit', 'quit', or Ctrl-D.", stacklevel=1)
Gated Recurrent Unit (GRU)
In 2014, a new, promising design for RNN units called Gated Recurrent Unit was published (https://arxiv.org/abs/1412.3555)
GRUs have performed similarly to LSTMs, but are slightly simpler in design:
- GRU has just two gates: "update" and "reset" (instead of the input, output, and forget in LSTM)
- update controls how to modify (weight and keep) cell state
- reset controls how new input is mixed (weighted) with/against memorized state
- there is no output gate, so the cell state is propagated out -- i.e., there is no "hidden" state that is separate from the generated output state

Which one should you use for which applications? The jury is still out -- this is an area for experimentation!
Using GRUs in Keras
... is as simple as using the built-in GRU class (https://keras.io/layers/recurrent/)
If you are working with RNNs, spend some time with docs to go deeper, as we have just barely scratched the surface here, and there are many "knobs" to turn that will help things go right (or wrong).
'''Example script to generate text from Nietzsche's writings.
At least 20 epochs are required before the generated text
starts sounding coherent.
It is recommended to run this script on GPU, as recurrent
networks are quite computationally intensive.
If you try this script on new data, make sure your corpus
has at least ~100k characters. ~1M is better.
'''
from __future__ import print_function
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LSTM
from keras.optimizers import RMSprop
from keras.utils.data_utils import get_file
import numpy as np
import random
import sys
path = get_file('nietzsche.txt', origin='https://s3.amazonaws.com/text-datasets/nietzsche.txt')
text = open(path).read().lower()
print('corpus length:', len(text))
chars = sorted(list(set(text)))
print('total chars:', len(chars))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
# cut the text in semi-redundant sequences of maxlen characters
maxlen = 40
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
print('nb sequences:', len(sentences))
print('Vectorization...')
X = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
corpus length: 600893
total chars: 57
nb sequences: 200285
Vectorization...
ls
conf
derby.log
eventlogs
ganglia
logs
len(sentences), maxlen, len(chars)
X
What Does Our Nietzsche Generator Produce?
Here are snapshots from middle and late in a training run.
Iteration 19
Iteration 19
Epoch 1/1
200287/200287 [==============================] - 262s - loss: 1.3908
----- diversity: 0.2
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions of the present of the supersially and the soul. the spirituality of the same of the soul. the protect and in the states to the supersially and the soul, in the supersially the supersially and the concerning and in the most conscience of the soul. the soul. the concerning and the substances, and the philosophers in the sing"--that is the most supersiall and the philosophers of the supersially of t
----- diversity: 0.5
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions are more there is the scientific modern to the head in the concerning in the same old will of the excited of science. many all the possible concerning such laugher according to when the philosophers sense of men of univerself, the most lacked same depresse in the point, which is desires of a "good (who has senses on that one experiencess which use the concerning and in the respect of the same ori
----- diversity: 1.0
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions expressions--are interest person from indeed to ordinapoon as or one of
the uphamy, state is rivel stimromannes are lot man of soul"--modile what he woulds hope in a riligiation, is conscience, and you amy, surposit to advanced torturily
and whorlon and perressing for accurcted with a lot us in view, of its own vanity of their natest"--learns, and dis predeceared from and leade, for oted those wi
----- diversity: 1.2
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions of
rutould chinates
rested exceteds to more saarkgs testure carevan, accordy owing before fatherly rifiny,
thrurgins of novelts "frous inventive earth as dire!ition he
shate out of itst sacrifice, in this
mectalical
inworle, you
adome enqueres to its ighter. he often. once even with ded threaten"! an eebirelesifist.
lran innoting
with we canone acquire at them crarulents who had prote will out t
Iteration 32
Iteration 32
Epoch 1/1
200287/200287 [==============================] - 255s - loss: 1.3830
----- diversity: 0.2
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, and in the great present of the sort of the strangern that is and in the sologies and the experiences and the present of the present and science of the probably a subject of the subject of the morality and morality of the soul the experiences the morality of the experiences of the conscience in the soul and more the experiences the strangere and present the rest the strangere and individual of th
----- diversity: 0.5
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, and in the morality of which we knows upon the english and insigning things be exception of
consequences of the man and explained its more in the senses for the same ordinary and the sortarians and subjects and simily in a some longing the destiny ordinary. man easily that has been the some subject and say, and and and and does not to power as all the reasonable and distinction of this one betray
----- diversity: 1.0
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, surrespossifilice view and life fundamental worthing more sirer. holestly
and whan to be
dream. in whom hand that one downgk edplenius will almost eyes brocky that we wills stupid dor
oborbbill to be dimorable
great excet of ifysabless. the good take the historical yet right by guntend, and which fuens the irrelias in literals in finally to the same flild, conditioned when where prom. it has behi
----- diversity: 1.2
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, easily achosed time mantur makeches on this
vanity, obcame-scompleises. but inquire-calr ever powerfully smorais: too-wantse; when thoue
conducting
unconstularly without least gainstyfyerfulled to wo
has upos
among uaxqunct what is mell "loves and
lamacity what mattery of upon the a. and which oasis seour schol
to power: the passion sparabrated will. in his europers raris! what seems to these her
Iteration 38
Iteration 38
Epoch 1/1
200287/200287 [==============================] - 256s - loss: 7.6662
----- diversity: 0.2
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughteesen a a a= at ae i is es4 iei aatee he a a ac oyte in ioie aan a atoe aie ion a atias a ooe o e tin exanat moe ao is aon e a ntiere t i in ate an on a e as the a ion aisn ost aed i i ioiesn les?ane i ee to i o ate o igice thi io an a xen an ae an teane one ee e alouieis asno oie on i a a ae s as n io a an e a ofe e oe ehe it aiol s a aeio st ior ooe an io e ot io o i aa9em aan ev a
----- diversity: 0.5
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughteese a on eionea] aooooi ate uo e9l hoe atae s in eaae an on io]e nd ast aais ta e od iia ng ac ee er ber in ==st a se is ao o e as aeian iesee tee otiane o oeean a ieatqe o asnone anc
oo a t
tee sefiois to an at in ol asnse an o e e oo ie oae asne at a ait iati oese se a e p ie peen iei ien o oot inees engied evone t oen oou atipeem a sthen ion assise ti a a s itos io ae an eees as oi
----- diversity: 1.0
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughteena te e ore te beosespeehsha ieno atit e ewge ou ino oo oee coatian aon ie ac aalle e a o die eionae oa att uec a acae ao a an eess as
o i a io a oe a e is as oo in ene xof o oooreeg ta m eon al iii n p daesaoe n ite o ane tio oe anoo t ane
s i e tioo ise s a asi e ana ooe ote soueeon io on atieaneyc ei it he se it is ao e an ime ane on eronaa ee itouman io e ato an ale a mae taoa ien
----- diversity: 1.2
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughti o aa e2senoees yi i e datssateal toeieie e a o zanato aal arn aseatli oeene aoni le eoeod t aes a isoee tap e o . is oi astee an ea titoe e a exeeee thui itoan ain eas a e bu inen ao ofa ie e e7n anae ait ie a ve er inen ite
as oe of heangi eestioe orasb e fie o o o a eean o ot odeerean io io oae ooe ne " e istee esoonae e terasfioees asa ehainoet at e ea ai esoon ano a p eesas e aitie
(raaz)
'Mind the Hype' around AI
Pay attention to biases in various media.
- Guardian: 'He began to eat Hermione's family': bot tries to write Harry Potter book – and fails in magic ways After being fed all seven Potter tales, a predictive keyboard has produced a tale that veers from almost genuine to gloriously bonkers
- Business Insider: There is a new chapter in Harry Potter's story — and it was written by artificial intelligence ... The writing is mostly weird and borderline comical, but the machine managed to partly reproduce original writer J.K. Rowling's writing style.
When your managers get "psyched" about how AI will solve all the problems and your sales teams are dreaming hard - keep it cool and manage their expectations as a practical data scientist who is humbled by the hard reality of additions, multiplications and conditionals under the hood.
'Mind the Ethics'
Don't forget to ask how your data science pipelines could adversely affect peoples: * A great X-mas gift to yourself: https://weaponsofmathdestructionbook.com/ * Another one to make you braver and calmer: https://www.schneier.com/books/dataandgoliath/
Don't forget that Data Scientists can be put behind bars for "following orders" from your boss to "make magic happen". * https://www.datasciencecentral.com/profiles/blogs/doing-illegal-data-science-without-knowing-it * https://timesofindia.indiatimes.com/india/forecast-of-poll-results-illegal-election-commission/articleshow/57927839.cms * https://spectrum.ieee.org/cars-that-think/at-work/education/vw-scandal-shocking-but-not-surprising-ethicists-say * ...