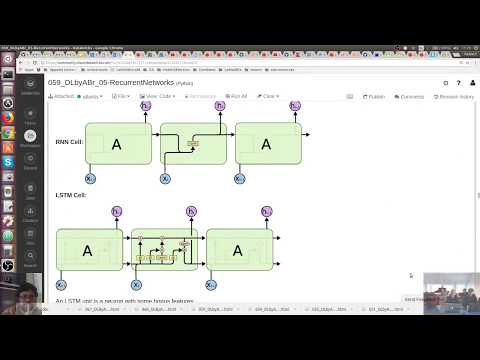
This notebook series was updated from the previous one sds-2-x-dl to work with Spark 3.0.1 and Python3+. The notebook series was updated on 2021-01-18. See changes from previous version in table below as well as current flaws that needs revision.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Table of changes and current flaws
| Notebook | Changes | Current flaws |
|---|---|---|
| 049 | cmd6 & cmd15: Picture missing | |
| 051 | cmd9: Changed syntax with dataframes in Pandas. Changed to df.loc for it to work properly. Also changed all .asmatrix() to .values since asmatrix() will be depreciated in future versions | |
| 053 | cmd4: Python WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/opdeflibrary.py:263: colocatewith (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version. Instructions for updating: Colocations handled automatically by placer. <tf.Variable 'y:0' shape=() dtype=int32ref> | |
| 054 | cmd15: Python WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/opdeflibrary.py:263: colocatewith (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version. Instructions for updating: Colocations handled automatically by placer. <tf.Variable 'y:0' shape=() dtype=int32ref> | |
| 055 | cmd25: Changed parameter in Dropout layer to rate=1-keepprob (see comments in code) since keepprob will be depreciated in future versions. | |
| 057 | cmd9: Changed parameter in Dropout layer to rate=1-keepprob (see comments in code) since keepprob will be depreciated in future versions. | cmd4: Python WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/opdeflibrary.py:263: colocatewith (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version. Instructions for updating: Colocations handled automatically by placer. <tf.Variable 'y:0' shape=() dtype=int32ref>, WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/mathops.py:3066: toint32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version. Instructions for updating: Use tf.cast instead. |
| 058 | cmd7 & cmd9: Updated path to cifar-10-batches-py | cmd17: Python WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/opdeflibrary.py:263: colocatewith (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version. Instructions for updating: Colocations handled automatically by placer. <tf.Variable 'y:0' shape=() dtype=int32ref>, WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/mathops.py:3066: toint32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version. Instructions for updating: Use tf.cast instead. |
| 060 | cmd2: Python WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/opdeflibrary.py:263: colocatewith (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version. Instructions for updating: Colocations handled automatically by placer. <tf.Variable 'y:0' shape=() dtype=int32ref>, WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/mathops.py:3066: toint32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version. Instructions for updating: Use tf.cast instead. | |
| 062 | cmd21: Changed parameter in Dropout layer to rate=1-keepprob (see comments in code) since keepprob will be depreciated in future versions. | |
| 063 | cmd16-cmd18: Does not work to mount on dbfs directly with save_weights() in keras. Workaround: Save first locally on tmp and then move files to dbfs. See https://github.com/h5py/h5py/issues/709 | cmd16: Python WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/opdeflibrary.py:263: colocatewith (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version. Instructions for updating: Colocations handled automatically by placer. <tf.Variable 'y:0' shape=() dtype=int32ref>, WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/mathops.py:3066: toint32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version. Instructions for updating: Use tf.cast instead. |
ScaDaMaLe Course site and book
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
This is Raaz's update of Siva's whirl-wind compression of the free Google's DL course in Udacity https://www.youtube.com/watch?v=iDyeK3GvFpo for Adam Briendel's DL modules that will follow.
Deep learning: A Crash Introduction
This notebook provides an introduction to Deep Learning. It is meant to help you descend more fully into these learning resources and references:
- Udacity's course on Deep Learning https://www.udacity.com/course/deep-learning--ud730 by Google engineers: Arpan Chakraborty and Vincent Vanhoucke and their full video playlist:
- Neural networks and deep learning http://neuralnetworksanddeeplearning.com/ by Michael Nielsen
- Deep learning book http://www.deeplearningbook.org/ by Ian Goodfellow, Yoshua Bengio and Aaron Courville
- Deep learning - buzzword for Artifical Neural Networks
- What is it?
- Supervised learning model - Classifier
- Unsupervised model - Anomaly detection (say via auto-encoders)
- Needs lots of data
- Online learning model - backpropogation
- Optimization - Stochastic gradient descent
- Regularization - L1, L2, Dropout
- Supervised
- Fully connected network
- Convolutional neural network - Eg: For classifying images
- Recurrent neural networks - Eg: For use on text, speech
- Unsupervised
- Autoencoder
A quick recap of logistic regression / linear models
(watch now 46 seconds from 4 to 50):
-- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
Regression
y = mx + c
Another way to look at a linear model
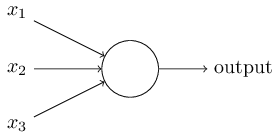
-- Image Credit: Michael Nielsen
Recap - Gradient descent
(1:54 seconds):
-- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
Recap - Stochastic Gradient descent
(2:25 seconds):
(1:28 seconds):
-- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
HOGWILD! Parallel SGD without locks http://i.stanford.edu/hazy/papers/hogwild-nips.pdf
Why deep learning? - Linear model
(24 seconds - 15 to 39):
-- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
ReLU - Rectified linear unit or Rectifier - max(0, x)
-- Image Credit: Wikipedia
Neural Network
Watch now (45 seconds, 0-45)
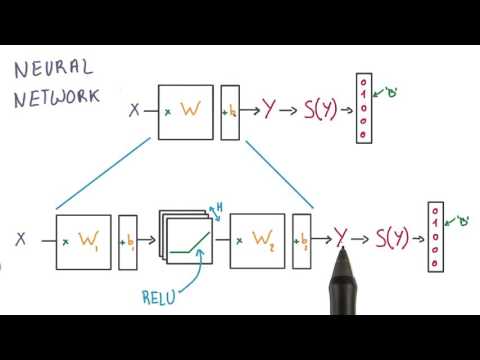 *** -- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
*** -- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
Is decision tree a linear model? http://datascience.stackexchange.com/questions/6787/is-decision-tree-algorithm-a-linear-or-nonlinear-algorithm
Neural Network ***  *** -- Image credit: Wikipedia
*** -- Image credit: Wikipedia
Multiple hidden layers
 *** -- Image credit: Michael Nielsen
*** -- Image credit: Michael Nielsen
What does it mean to go deep? What do each of the hidden layers learn?
Watch now (1:13 seconds)
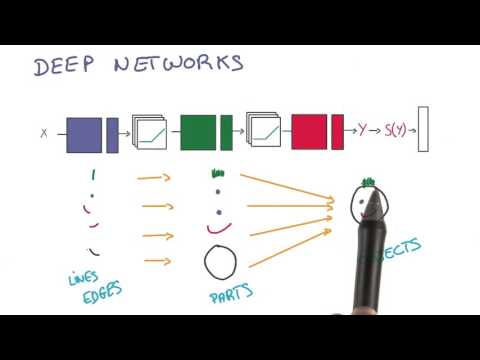 *** -- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
*** -- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
Chain rule
\[ (f \circ g)\prime = (f\prime \circ g) \cdot g\prime \] *** ***
Chain rule in neural networks
Watch later (55 seconds)
 *** -- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
*** -- Video Credit: Udacity's deep learning by Arpan Chakraborthy and Vincent Vanhoucke
Backpropogation
To properly understand this you are going to minimally need 20 minutes or so, depending on how rusty your maths is now.
First go through this carefully: * https://stats.stackexchange.com/questions/224140/step-by-step-example-of-reverse-mode-automatic-differentiation
Watch later (9:55 seconds)
How do you set the learning rate? - Step size in SGD?
there is a lot more... including newer frameworks for automating these knows using probabilistic programs (but in non-distributed settings as of Dec 2017).
So far we have only seen fully connected neural networks, now let's move into more interesting ones that exploit spatial locality and nearness patterns inherent in certain classes of data, such as image data.
Convolutional Neural Networks
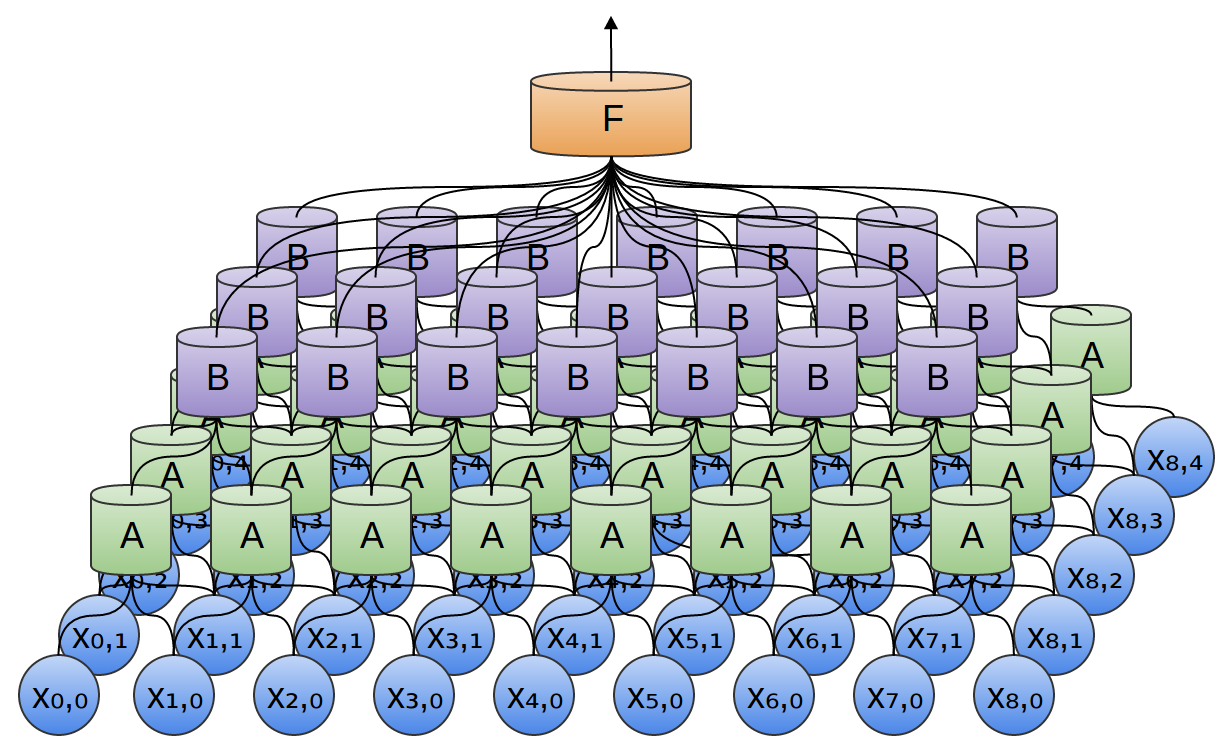 *** Watch now (3:55)
[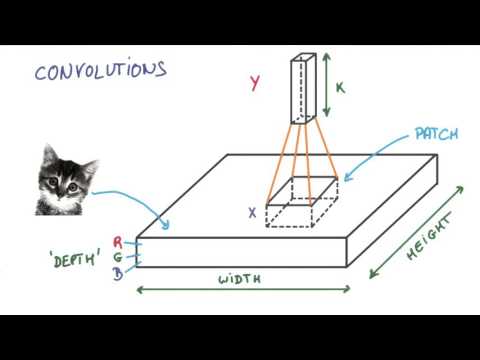](https://www.youtube.com/watch?v=jajksuQW4mc)
***
*** Watch now (3:55)
[](https://www.youtube.com/watch?v=jajksuQW4mc)
***
- Alex Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton - https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
- Convolutional Neural networks blog - http://colah.github.io/posts/2014-07-Conv-Nets-Modular/
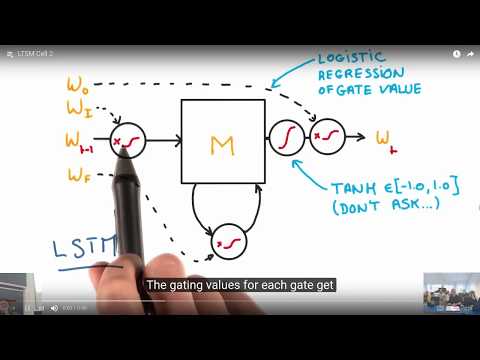
Recurrent neural network
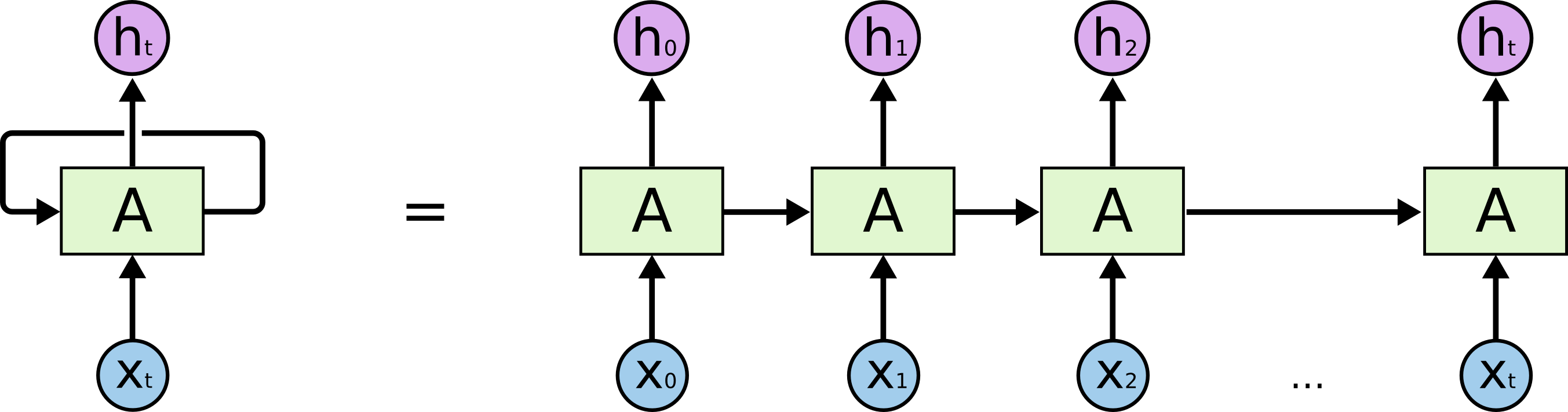 http://colah.github.io/posts/2015-08-Understanding-LSTMs/
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
http://karpathy.github.io/2015/05/21/rnn-effectiveness/
*** Watch (3:55)
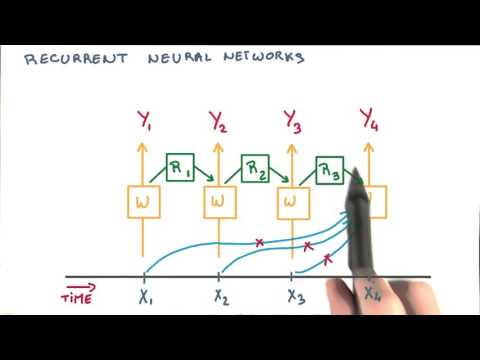
LSTM - Long short term memory

GRU - Gated recurrent unit
The more recent improvement over CNNs are called capsule networks by Hinton. Check them out here if you want to prepare for your future interview question in 2017/2018 or so...:
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Introduction to Deep Learning
Theory and Practice with TensorFlow and Keras

https://arxiv.org/abs/1508.06576
by the end of this course, this paper and project will be accessible to you!
Schedule
- Intro
- TensorFlow Basics
- Artificial Neural Networks
- Multilayer ("Deep") Feed-Forward Networks
- Training Neural Nets
- Convolutional Networks
- Recurrent Nets, LSTM, GRU
- Generative Networks / Patterns
- Intro to Reinforcement Learning
- Operations in the Real World
Instructor: Adam Breindel

Contact: https://www.linkedin.com/in/adbreind - adbreind@gmail.com
- Almost 20 years building systems for startups and large enterprises
- 10 years teaching front- and back-end technology
Interesting projects...
- My first full-time job in tech involved streaming neural net fraud scoring (debit cards)
- Realtime & offline analytics for banking
- Music synchronization and licensing for networked jukeboxes
Industries
- Finance / Insurance, Travel, Media / Entertainment, Government
Class Goals
- Understand deep learning!
- Acquire an intiution and feeling for how and why and when it works, so you can use it!
- No magic! (or at least very little magic)
- We don't want to have a workshop where we install and demo some magical, fairly complicated thing, and we watch it do something awesome, and handwave, and go home
- That's great for generating excitement, but leaves
- Theoretical mysteries -- what's going on? do I need a Ph.D. in Math or Statistics to do this?
- Practical problems -- I have 10 lines of code but they never run because my tensor is the wrong shape!
- That's great for generating excitement, but leaves
- We'll focus on TensorFlow and Keras
- But 95% should be knowledge you can use with frameworks too: Intel BigDL, Baidu PaddlePaddle, NVIDIA Digits, MXNet, etc.
Deep Learning is About Machines Finding Patterns and Solving Problems
So let's start by diving right in and discussing an interesing problem:
MNIST Digits Dataset
Mixed National Institute of Standards and Technology
Called the "Drosophila" of Machine Learning
Likely the most common single dataset out there in deep learning, just complex enough to be interesting and useful for benchmarks.
"If your code works on MNIST, that doesn't mean it will work everywhere; but if it doesn't work on MNIST, it probably won't work anywhere" :)

What is the goal?
Convert an image of a handwritten character into the correct classification (i.e., which character is it?)
This is nearly trivial for a human to do! Most toddlers can do this with near 100% accuracy, even though they may not be able to count beyond 10 or perform addition.
Traditionally this had been quite a hard task for a computer to do. 99% was not achieved until ~1998. Consistent, easy success at that level was not until 2003 or so.
Let's describe the specific problem in a little more detail
-
Each image is a 28x28 pixel image
- originally monochrome; smoothed to gray; typically inverted, so that "blank" pixels are black (zeros)
-
So the predictors are 784 (28 * 28 = 784) values, ranging from 0 (black / no ink when inverted) to 255 (white / full ink when inverted)
-
The response -- what we're trying to predict -- is the number that the image represents
- the response is a value from 0 to 9
- since there are a small number of discrete catagories for the responses, this is a classification problem, not a regression problem
- there are 10 classes
-
We have, for each data record, predictors and a response to train against, so this is a supervised learning task
-
The dataset happens to come partitioned into a training set (60,000 records) and a test set (10,000 records)
- We'll "hold out" the test set and not train on it
-
Once our model is trained, we'll use it to predict (or perform inference) on the test records, and see how well our trained model performs on unseen test data
- We might want to further split the training set into a validation set or even several K-fold partitions to evaluate as we go
-
As humans, we'll probably measure our success by using accuracy as a metric: What fraction of the examples are correctly classified by the model?
- However, for training, it makes more sense to use cross-entropy to measure, correct, and improve the model. Cross-entropy has the advantage that instead of just counting "right or wrong" answers, it provides a continuous measure of "how wrong (or right)" an answer is. For example, if the correct answer is "1" then the answer "probably a 7, maybe a 1" is wrong, but less wrong than the answer "definitely a 7"
-
Do we need to pre-process the data? Depending on the model we use, we may want to ...
- Scale the values, so that they range from 0 to 1, or so that they measure in standard deviations
- Center the values so that 0 corresponds to the (raw central) value 127.5, or so that 0 corresponds to the mean
What might be characteristics of a good solution?
- As always, we need to balance variance (malleability of the model in the face of variation in the sample training data) and bias (strength/inflexibility of assumptions built in to the modeling method)
- We a model with a good amount of capacity to represent different patterns in the training data (e.g., different handwriting styles) while not overfitting and learning too much about specific training instances
- We'd like a probabalistic model that tells us the most likely classes given the data and assumptions (for example, in the U.S., a one is often written with a vertical stroke, whereas in Germany it's usually written with 2 strokes, closer to a U.S. 7)
Going a little further,
- an ideal modeling approach might perform feature selection on its own deciding which pixels and combinations of pixels are most informative
- in order to be robust to varying data, a good model might learn hierarchical or abstract features like lines, angles, curves and loops that we as humans use to teach, learn, and distinguish Arabic numerals from each other
- it would be nice to add some basic domain knowledge like these features aren't arbitrary slots in a vector, but are parts of a 2-dimensional image where the contents are roughly axis-aligned and translation invariant -- after all, a "7" is still a "7" even if we move it around a bit on the page
Lastly, it would be great to have a framework that is flexible enough to adapt to similar tasks -- say, Greek, Cyrillic, or Chinese handwritten characters, not just digits.
Let's compare some modeling techniques...
Decision Tree
👍 High capacity
👎 Can be hard to generalize; prone to overfit; fragile for this kind of task
👎 Dedicated training algorithm (traditional approach is not directly a gradient-descent optimization problem)
👍 Performs feature selection / PCA implicitly
(Multiclass) Logistic Regression
👎 Low capacity/variance -> High bias
👍 Less overfitting
👎 Less fitting (accuracy)

Kernelized Support Vector Machine (e.g., RBF)
👍 Robust capacity, good bias-variance balance
👎 Expensive to scale in terms of features or instances
👍 Amenable to "online" learning (http://www.isn.ucsd.edu/papers/nips00_inc.pdf)
👍 State of the art for MNIST prior to the widespread use of deep learning!
Deep Learning
It turns out that a model called a convolutional neural network meets all of our goals and can be trained to human-level accuracy on this task in just a few minutes. We will solve MNIST with this sort of model today.
But we will build up to it starting with the simplest neural model.
Mathematical statistical caveat: Note that ML algorithmic performance measures such as 99% or 99.99% as well as their justification by comparisons to "typical" human performance measures from a randomised surveyable population actually often make significant mathematical assumptions that may be violated under the carpet. Some concrete examples include, the size and nature of the training data and their generalizability to live decision problems based on empirical risk minisation principles like cross-validation. These assumpitons are usually harmless and can be time-saving for most problems like recommending songs in Spotify or shoes in Amazon. It is important to bear in mind that there are problems that should guarantee worst case scenario avoidance, like accidents with self-driving cars or global extinction event cause by mathematically ambiguous assumptions in the learning algorithms of say near-Earth-Asteroid mining artificially intelligent robots!
Installations (PyPI rules)
- tensorflow==1.13.1 (worked also on 1.3.0)
- keras==2.2.4 (worked also on 2.0.6)
- dist-keras==0.2.1 (worked also on 0.2.0) Python 3.0 compatible. So make sure cluster has Python 3.0
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Artificial Neural Network - Perceptron
The field of artificial neural networks started out with an electromechanical binary unit called a perceptron.
The perceptron took a weighted set of input signals and chose an ouput state (on/off or high/low) based on a threshold.

(raaz) Thus, the perceptron is defined by:
\[ f(1, x_1,x_2,\ldots , x_n , ; , w_0,w_1,w_2,\ldots , w_n) = \begin{cases} 1 & \text{if} \quad \sum_{i=0}^n w_i x_i > 0 \ 0 & \text{otherwise} \end{cases} \] and implementable with the following arithmetical and logical unit (ALU) operations in a machine:
- n inputs from one \(n\)-dimensional data point: \(x_1,x_2,\ldots x_n , \in , \mathbb{R}^n\)
- arithmetic operations
- n+1 multiplications
- n additions
- boolean operations
- one if-then on an inequality
- one output \(o \in {0,1}\), i.e., \(o\) belongs to the set containing \(0\) and \(1\)
- n+1 parameters of interest
This is just a hyperplane given by a dot product of \(n+1\) known inputs and \(n+1\) unknown parameters that can be estimated. This hyperplane can be used to define a hyperplane that partitions \(\mathbb{R}^{n+1}\), the real Euclidean space, into two parts labelled by the outputs \(0\) and \(1\).
The problem of finding estimates of the parameters, \((\hat{w}_0,\hat{w}_1,\hat{w}_2,\ldots \hat{w}_n) \in \mathbb{R}^{(n+1)}\), in some statistically meaningful manner for a predicting task by using the training data given by, say \(k\) labelled points, where you know both the input and output: \[ \left( ( , 1, x_1^{(1)},x_2^{(1)}, \ldots x_n^{(1)}), (o^{(1)}) , ), , ( , 1, x_1^{(2)},x_2^{(2)}, \ldots x_n^{(2)}), (o^{(2)}) , ), , \ldots , , ( , 1, x_1^{(k)},x_2^{(k)}, \ldots x_n^{(k)}), (o^{(k)}) , ) \right) , \in , (\mathbb{R}^{n+1} \times { 0,1 } )^k \] is the machine learning problem here.
Succinctly, we are after a random mapping, denoted below by \(\mapsto_{\rightsquigarrow}\), called the estimator: \[
(\mathbb{R}^{n+1} \times {0,1})^k \mapsto_{\rightsquigarrow} , \left( , \mathtt{model}( (1,x_1,x_2,\ldots,x_n) ,;, (\hat{w}_0,\hat{w}_1,\hat{w}_2,\ldots \hat{w}_n)) : \mathbb{R}^{n+1} \to {0,1} , \right)
\] which takes random labelled dataset (to understand random here think of two scientists doing independent experiments to get their own training datasets) of size \(k\) and returns a model. These mathematical notions correspond exactly to the estimator and model (which is a transformer) in the language of Apache Spark's Machine Learning Pipleines we have seen before.
We can use this transformer for prediction of unlabelled data where we only observe the input and what to know the output under some reasonable assumptions.
Of course we want to be able to generalize so we don't overfit to the training data using some empirical risk minisation rule such as cross-validation. Again, we have seen these in Apache Spark for other ML methods like linear regression and decision trees.
If the output isn't right, we can adjust the weights, threshold, or bias (\(x_0\) above)
The model was inspired by discoveries about the neurons of animals, so hopes were quite high that it could lead to a sophisticated machine. This model can be extended by adding multiple neurons in parallel. And we can use linear output instead of a threshold if we like for the output.
If we were to do so, the output would look like \({x \cdot w} + w_0\) (this is where the vector multiplication and, eventually, matrix multiplication, comes in)
When we look at the math this way, we see that despite this being an interesting model, it's really just a fancy linear calculation.
And, in fact, the proof that this model -- being linear -- could not solve any problems whose solution was nonlinear ... led to the first of several "AI / neural net winters" when the excitement was quickly replaced by disappointment, and most research was abandoned.
Linear Perceptron
We'll get to the non-linear part, but the linear perceptron model is a great way to warm up and bridge the gap from traditional linear regression to the neural-net flavor.
Let's look at a problem -- the diamonds dataset from R -- and analyze it using two traditional methods in Scikit-Learn, and then we'll start attacking it with neural networks!
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error
input_file = "/dbfs/databricks-datasets/Rdatasets/data-001/csv/ggplot2/diamonds.csv"
df = pd.read_csv(input_file, header = 0)
import IPython.display as disp
pd.set_option('display.width', 200)
disp.display(df[:10])
Unnamed: 0 carat cut color clarity ... table price x y z
0 1 0.23 Ideal E SI2 ... 55.0 326 3.95 3.98 2.43
1 2 0.21 Premium E SI1 ... 61.0 326 3.89 3.84 2.31
2 3 0.23 Good E VS1 ... 65.0 327 4.05 4.07 2.31
3 4 0.29 Premium I VS2 ... 58.0 334 4.20 4.23 2.63
4 5 0.31 Good J SI2 ... 58.0 335 4.34 4.35 2.75
5 6 0.24 Very Good J VVS2 ... 57.0 336 3.94 3.96 2.48
6 7 0.24 Very Good I VVS1 ... 57.0 336 3.95 3.98 2.47
7 8 0.26 Very Good H SI1 ... 55.0 337 4.07 4.11 2.53
8 9 0.22 Fair E VS2 ... 61.0 337 3.87 3.78 2.49
9 10 0.23 Very Good H VS1 ... 61.0 338 4.00 4.05 2.39
[10 rows x 11 columns]
df2 = df.drop(df.columns[0], axis=1)
disp.display(df2[:3])
carat cut color clarity depth table price x y z
0 0.23 Ideal E SI2 61.5 55.0 326 3.95 3.98 2.43
1 0.21 Premium E SI1 59.8 61.0 326 3.89 3.84 2.31
2 0.23 Good E VS1 56.9 65.0 327 4.05 4.07 2.31
df3 = pd.get_dummies(df2) # this gives a one-hot encoding of categorial variables
disp.display(df3.iloc[:3, 7:18])
cut_Fair cut_Good cut_Ideal ... color_G color_H color_I
0 0 0 1 ... 0 0 0
1 0 0 0 ... 0 0 0
2 0 1 0 ... 0 0 0
[3 rows x 11 columns]
# pre-process to get y
y = df3.iloc[:,3:4].values.flatten()
y.flatten()
# preprocess and reshape X as a matrix
X = df3.drop(df3.columns[3], axis=1).values
np.shape(X)
# break the dataset into training and test set with a 75% and 25% split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
# Define a decisoin tree model with max depth 10
dt = DecisionTreeRegressor(random_state=0, max_depth=10)
# fit the decision tree to the training data to get a fitted model
model = dt.fit(X_train, y_train)
# predict the features or X values of the test data using the fitted model
y_pred = model.predict(X_test)
# print the MSE performance measure of the fit by comparing the predicted versus the observed values of y
print("RMSE %f" % np.sqrt(mean_squared_error(y_test, y_pred)) )
RMSE 727.042036
from sklearn import linear_model
# Do the same with linear regression and not a worse MSE
lr = linear_model.LinearRegression()
linear_model = lr.fit(X_train, y_train)
y_pred = linear_model.predict(X_test)
print("RMSE %f" % np.sqrt(mean_squared_error(y_test, y_pred)) )
RMSE 1124.086095
Now that we have a baseline, let's build a neural network -- linear at first -- and go further.
Neural Network with Keras
Keras is a High-Level API for Neural Networks and Deep Learning

"Being able to go from idea to result with the least possible delay is key to doing good research."
Maintained by Francois Chollet at Google, it provides
- High level APIs
- Pluggable backends for Theano, TensorFlow, CNTK, MXNet
- CPU/GPU support
- The now-officially-endorsed high-level wrapper for TensorFlow; a version ships in TF
- Model persistence and other niceties
- JavaScript, iOS, etc. deployment
- Interop with further frameworks, like DeepLearning4J, Spark DL Pipelines ...
Well, with all this, why would you ever not use Keras?
As an API/Facade, Keras doesn't directly expose all of the internals you might need for something custom and low-level ... so you might need to implement at a lower level first, and then perhaps wrap it to make it easily usable in Keras.
Mr. Chollet compiles stats (roughly quarterly) on "[t]he state of the deep learning landscape: GitHub activity of major libraries over the past quarter (tickets, forks, and contributors)."
(October 2017: https://twitter.com/fchollet/status/915366704401719296; https://twitter.com/fchollet/status/915626952408436736)
GitHub | Research |
Keras has wide adoption in industry

We'll build a "Dense Feed-Forward Shallow" Network:
(the number of units in the following diagram does not exactly match ours) 
Grab a Keras API cheat sheet from https://s3.amazonaws.com/assets.datacamp.com/blogassets/KerasCheatSheetPython.pdf
from keras.models import Sequential
from keras.layers import Dense
# we are going to add layers sequentially one after the other (feed-forward) to our neural network model
model = Sequential()
# the first layer has 30 nodes (or neurons) with input dimension 26 for our diamonds data
# we will use Nomal or Guassian kernel to initialise the weights we want to estimate
# our activation function is linear (to mimic linear regression)
model.add(Dense(30, input_dim=26, kernel_initializer='normal', activation='linear'))
# the next layer is for the response y and has only one node
model.add(Dense(1, kernel_initializer='normal', activation='linear'))
# compile the model with other specifications for loss and type of gradient descent optimisation routine
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mean_squared_error'])
# fit the model to the training data using stochastic gradient descent with a batch-size of 200 and 10% of data held out for validation
history = model.fit(X_train, y_train, epochs=10, batch_size=200, validation_split=0.1)
scores = model.evaluate(X_test, y_test)
print()
print("test set RMSE: %f" % np.sqrt(scores[1]))
Using TensorFlow backend.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 36409 samples, validate on 4046 samples
Epoch 1/10
200/36409 [..............................] - ETA: 30s - loss: 24515974.0000 - mean_squared_error: 24515974.0000
8600/36409 [======>.......................] - ETA: 0s - loss: 30972551.0233 - mean_squared_error: 30972551.0233
16400/36409 [============>.................] - ETA: 0s - loss: 31092082.1707 - mean_squared_error: 31092082.1707
24400/36409 [===================>..........] - ETA: 0s - loss: 30821887.3934 - mean_squared_error: 30821887.3934
33200/36409 [==========================>...] - ETA: 0s - loss: 30772256.5783 - mean_squared_error: 30772256.5783
36409/36409 [==============================] - 0s 12us/step - loss: 30662987.2877 - mean_squared_error: 30662987.2877 - val_loss: 30057002.5457 - val_mean_squared_error: 30057002.5457
Epoch 2/10
200/36409 [..............................] - ETA: 0s - loss: 27102510.0000 - mean_squared_error: 27102510.0000
9000/36409 [======>.......................] - ETA: 0s - loss: 28506919.5556 - mean_squared_error: 28506919.5556
17600/36409 [=============>................] - ETA: 0s - loss: 27940962.7727 - mean_squared_error: 27940962.7727
26200/36409 [====================>.........] - ETA: 0s - loss: 27211811.0076 - mean_squared_error: 27211811.0076
34800/36409 [===========================>..] - ETA: 0s - loss: 26426392.1034 - mean_squared_error: 26426392.1034
36409/36409 [==============================] - 0s 6us/step - loss: 26167957.1320 - mean_squared_error: 26167957.1320 - val_loss: 23785895.3554 - val_mean_squared_error: 23785895.3554
Epoch 3/10
200/36409 [..............................] - ETA: 0s - loss: 17365908.0000 - mean_squared_error: 17365908.0000
7200/36409 [====>.........................] - ETA: 0s - loss: 22444847.5556 - mean_squared_error: 22444847.5556
16000/36409 [============>.................] - ETA: 0s - loss: 21373980.3000 - mean_squared_error: 21373980.3000
24000/36409 [==================>...........] - ETA: 0s - loss: 21005080.0500 - mean_squared_error: 21005080.0500
31800/36409 [=========================>....] - ETA: 0s - loss: 20236407.7170 - mean_squared_error: 20236407.7170
36409/36409 [==============================] - 0s 7us/step - loss: 20020372.1159 - mean_squared_error: 20020372.1159 - val_loss: 18351806.8710 - val_mean_squared_error: 18351806.8710
Epoch 4/10
200/36409 [..............................] - ETA: 0s - loss: 17831442.0000 - mean_squared_error: 17831442.0000
8400/36409 [=====>........................] - ETA: 0s - loss: 17513972.2857 - mean_squared_error: 17513972.2857
17000/36409 [=============>................] - ETA: 0s - loss: 16829699.6941 - mean_squared_error: 16829699.6941
25600/36409 [====================>.........] - ETA: 0s - loss: 16673756.4375 - mean_squared_error: 16673756.4375
33800/36409 [==========================>...] - ETA: 0s - loss: 16443651.8225 - mean_squared_error: 16443651.8225
36409/36409 [==============================] - 0s 6us/step - loss: 16317392.6930 - mean_squared_error: 16317392.6930 - val_loss: 16164358.2887 - val_mean_squared_error: 16164358.2887
Epoch 5/10
200/36409 [..............................] - ETA: 0s - loss: 20413018.0000 - mean_squared_error: 20413018.0000
7400/36409 [=====>........................] - ETA: 0s - loss: 15570987.0000 - mean_squared_error: 15570987.0000
14800/36409 [===========>..................] - ETA: 0s - loss: 15013196.5405 - mean_squared_error: 15013196.5405
23400/36409 [==================>...........] - ETA: 0s - loss: 15246935.8034 - mean_squared_error: 15246935.8034
32000/36409 [=========================>....] - ETA: 0s - loss: 15250803.7375 - mean_squared_error: 15250803.7375
36409/36409 [==============================] - 0s 7us/step - loss: 15255931.8414 - mean_squared_error: 15255931.8414 - val_loss: 15730755.8908 - val_mean_squared_error: 15730755.8908
Epoch 6/10
200/36409 [..............................] - ETA: 0s - loss: 18564152.0000 - mean_squared_error: 18564152.0000
7600/36409 [=====>........................] - ETA: 0s - loss: 15086204.8421 - mean_squared_error: 15086204.8421
16200/36409 [============>.................] - ETA: 0s - loss: 15104538.2593 - mean_squared_error: 15104538.2593
24600/36409 [===================>..........] - ETA: 0s - loss: 15172120.3008 - mean_squared_error: 15172120.3008
32600/36409 [=========================>....] - ETA: 0s - loss: 15123702.1043 - mean_squared_error: 15123702.1043
36409/36409 [==============================] - 0s 7us/step - loss: 15066138.8398 - mean_squared_error: 15066138.8398 - val_loss: 15621212.2521 - val_mean_squared_error: 15621212.2521
Epoch 7/10
200/36409 [..............................] - ETA: 0s - loss: 12937932.0000 - mean_squared_error: 12937932.0000
8400/36409 [=====>........................] - ETA: 0s - loss: 15215220.5238 - mean_squared_error: 15215220.5238
16400/36409 [============>.................] - ETA: 0s - loss: 15116822.9268 - mean_squared_error: 15116822.9268
24600/36409 [===================>..........] - ETA: 0s - loss: 14993875.2439 - mean_squared_error: 14993875.2439
32600/36409 [=========================>....] - ETA: 0s - loss: 14956622.0184 - mean_squared_error: 14956622.0184
36409/36409 [==============================] - 0s 7us/step - loss: 14981999.6368 - mean_squared_error: 14981999.6368 - val_loss: 15533945.2353 - val_mean_squared_error: 15533945.2353
Epoch 8/10
200/36409 [..............................] - ETA: 0s - loss: 17393156.0000 - mean_squared_error: 17393156.0000
7800/36409 [=====>........................] - ETA: 0s - loss: 15290136.5128 - mean_squared_error: 15290136.5128
16200/36409 [============>.................] - ETA: 0s - loss: 15074332.1235 - mean_squared_error: 15074332.1235
24600/36409 [===================>..........] - ETA: 0s - loss: 14987445.0488 - mean_squared_error: 14987445.0488
33000/36409 [==========================>...] - ETA: 0s - loss: 14853941.5394 - mean_squared_error: 14853941.5394
36409/36409 [==============================] - 0s 7us/step - loss: 14896132.4141 - mean_squared_error: 14896132.4141 - val_loss: 15441119.5566 - val_mean_squared_error: 15441119.5566
Epoch 9/10
200/36409 [..............................] - ETA: 0s - loss: 12659630.0000 - mean_squared_error: 12659630.0000
8600/36409 [======>.......................] - ETA: 0s - loss: 14682766.8605 - mean_squared_error: 14682766.8605
17000/36409 [=============>................] - ETA: 0s - loss: 14851612.5882 - mean_squared_error: 14851612.5882
25600/36409 [====================>.........] - ETA: 0s - loss: 14755020.0234 - mean_squared_error: 14755020.0234
34200/36409 [===========================>..] - ETA: 0s - loss: 14854599.4737 - mean_squared_error: 14854599.4737
36409/36409 [==============================] - 0s 6us/step - loss: 14802259.4853 - mean_squared_error: 14802259.4853 - val_loss: 15339340.7177 - val_mean_squared_error: 15339340.7177
Epoch 10/10
200/36409 [..............................] - ETA: 0s - loss: 14473119.0000 - mean_squared_error: 14473119.0000
8600/36409 [======>.......................] - ETA: 0s - loss: 14292346.6512 - mean_squared_error: 14292346.6512
16200/36409 [============>.................] - ETA: 0s - loss: 14621621.4938 - mean_squared_error: 14621621.4938
24600/36409 [===================>..........] - ETA: 0s - loss: 14648206.4228 - mean_squared_error: 14648206.4228
33200/36409 [==========================>...] - ETA: 0s - loss: 14746160.4398 - mean_squared_error: 14746160.4398
36409/36409 [==============================] - 0s 7us/step - loss: 14699508.8054 - mean_squared_error: 14699508.8054 - val_loss: 15226518.1542 - val_mean_squared_error: 15226518.1542
32/13485 [..............................] - ETA: 0s
4096/13485 [========>.....................] - ETA: 0s
7040/13485 [==============>...............] - ETA: 0s
9920/13485 [=====================>........] - ETA: 0s
13485/13485 [==============================] - 0s 15us/step
test set RMSE: 3800.812819
model.summary() # do you understand why the number of parameters in layer 1 is 810? 26*30+30=810
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 30) 810
_________________________________________________________________
dense_2 (Dense) (None, 1) 31
=================================================================
Total params: 841
Trainable params: 841
Non-trainable params: 0
_________________________________________________________________
Notes:
- We didn't have to explicitly write the "input" layer, courtesy of the Keras API. We just said
input_dim=26on the first (and only) hidden layer. kernel_initializer='normal'is a simple (though not always optimal) weight initialization- Epoch: 1 pass over all of the training data
- Batch: Records processes together in a single training pass
How is our RMSE vs. the std dev of the response?
y.std()
Let's look at the error ...
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
display(fig)
Let's set up a "long-running" training. This will take a few minutes to converge to the same performance we got more or less instantly with our sklearn linear regression :)
While it's running, we can talk about the training.
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
import pandas as pd
input_file = "/dbfs/databricks-datasets/Rdatasets/data-001/csv/ggplot2/diamonds.csv"
df = pd.read_csv(input_file, header = 0)
df.drop(df.columns[0], axis=1, inplace=True)
df = pd.get_dummies(df, prefix=['cut_', 'color_', 'clarity_'])
y = df.iloc[:,3:4].values.flatten()
y.flatten()
X = df.drop(df.columns[3], axis=1).values
np.shape(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
model = Sequential()
model.add(Dense(30, input_dim=26, kernel_initializer='normal', activation='linear'))
model.add(Dense(1, kernel_initializer='normal', activation='linear'))
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mean_squared_error'])
history = model.fit(X_train, y_train, epochs=250, batch_size=100, validation_split=0.1, verbose=2)
scores = model.evaluate(X_test, y_test)
print("\nroot %s: %f" % (model.metrics_names[1], np.sqrt(scores[1])))
Train on 36409 samples, validate on 4046 samples
Epoch 1/250
- 1s - loss: 28387336.4384 - mean_squared_error: 28387336.4384 - val_loss: 23739923.0816 - val_mean_squared_error: 23739923.0816
Epoch 2/250
- 0s - loss: 18190573.9659 - mean_squared_error: 18190573.9659 - val_loss: 16213271.2121 - val_mean_squared_error: 16213271.2121
Epoch 3/250
- 0s - loss: 15172630.1573 - mean_squared_error: 15172630.1573 - val_loss: 15625113.6841 - val_mean_squared_error: 15625113.6841
Epoch 4/250
- 0s - loss: 14945745.1874 - mean_squared_error: 14945745.1874 - val_loss: 15453493.5042 - val_mean_squared_error: 15453493.5042
Epoch 5/250
- 0s - loss: 14767640.2591 - mean_squared_error: 14767640.2591 - val_loss: 15254403.9486 - val_mean_squared_error: 15254403.9486
Epoch 6/250
- 0s - loss: 14557887.6100 - mean_squared_error: 14557887.6100 - val_loss: 15019167.1374 - val_mean_squared_error: 15019167.1374
Epoch 7/250
- 0s - loss: 14309593.5448 - mean_squared_error: 14309593.5448 - val_loss: 14737183.8052 - val_mean_squared_error: 14737183.8052
Epoch 8/250
- 0s - loss: 14013285.0941 - mean_squared_error: 14013285.0941 - val_loss: 14407560.3356 - val_mean_squared_error: 14407560.3356
Epoch 9/250
- 0s - loss: 13656069.2042 - mean_squared_error: 13656069.2042 - val_loss: 13997285.5230 - val_mean_squared_error: 13997285.5230
Epoch 10/250
- 0s - loss: 13216458.2848 - mean_squared_error: 13216458.2848 - val_loss: 13489102.3277 - val_mean_squared_error: 13489102.3277
Epoch 11/250
- 0s - loss: 12677035.7927 - mean_squared_error: 12677035.7927 - val_loss: 12879791.1409 - val_mean_squared_error: 12879791.1409
Epoch 12/250
- 0s - loss: 12026548.9956 - mean_squared_error: 12026548.9956 - val_loss: 12144681.5783 - val_mean_squared_error: 12144681.5783
Epoch 13/250
- 0s - loss: 11261201.3992 - mean_squared_error: 11261201.3992 - val_loss: 11298467.2511 - val_mean_squared_error: 11298467.2511
Epoch 14/250
- 0s - loss: 10394848.5657 - mean_squared_error: 10394848.5657 - val_loss: 10359981.5892 - val_mean_squared_error: 10359981.5892
Epoch 15/250
- 0s - loss: 9464690.1582 - mean_squared_error: 9464690.1582 - val_loss: 9377032.8176 - val_mean_squared_error: 9377032.8176
Epoch 16/250
- 0s - loss: 8522523.9198 - mean_squared_error: 8522523.9198 - val_loss: 8407744.1396 - val_mean_squared_error: 8407744.1396
Epoch 17/250
- 0s - loss: 7614509.1284 - mean_squared_error: 7614509.1284 - val_loss: 7483504.2244 - val_mean_squared_error: 7483504.2244
Epoch 18/250
- 0s - loss: 6773874.9790 - mean_squared_error: 6773874.9790 - val_loss: 6642935.4123 - val_mean_squared_error: 6642935.4123
Epoch 19/250
- 0s - loss: 6029308.8020 - mean_squared_error: 6029308.8020 - val_loss: 5907274.1873 - val_mean_squared_error: 5907274.1873
Epoch 20/250
- 0s - loss: 5389141.6630 - mean_squared_error: 5389141.6630 - val_loss: 5281166.3648 - val_mean_squared_error: 5281166.3648
Epoch 21/250
- 0s - loss: 4860038.6980 - mean_squared_error: 4860038.6980 - val_loss: 4764607.7313 - val_mean_squared_error: 4764607.7313
Epoch 22/250
- 0s - loss: 4431739.1137 - mean_squared_error: 4431739.1137 - val_loss: 4351510.2142 - val_mean_squared_error: 4351510.2142
Epoch 23/250
- 0s - loss: 4094045.5128 - mean_squared_error: 4094045.5128 - val_loss: 4021251.9317 - val_mean_squared_error: 4021251.9317
Epoch 24/250
- 0s - loss: 3829986.6989 - mean_squared_error: 3829986.6989 - val_loss: 3757295.1629 - val_mean_squared_error: 3757295.1629
Epoch 25/250
- 0s - loss: 3623823.6510 - mean_squared_error: 3623823.6510 - val_loss: 3552794.5538 - val_mean_squared_error: 3552794.5538
Epoch 26/250
- 0s - loss: 3465635.4962 - mean_squared_error: 3465635.4962 - val_loss: 3393235.2467 - val_mean_squared_error: 3393235.2467
Epoch 27/250
- 0s - loss: 3340038.8348 - mean_squared_error: 3340038.8348 - val_loss: 3269279.0370 - val_mean_squared_error: 3269279.0370
Epoch 28/250
- 0s - loss: 3236200.2134 - mean_squared_error: 3236200.2134 - val_loss: 3156617.4010 - val_mean_squared_error: 3156617.4010
Epoch 29/250
- 0s - loss: 3150650.9059 - mean_squared_error: 3150650.9059 - val_loss: 3065790.8180 - val_mean_squared_error: 3065790.8180
Epoch 30/250
- 0s - loss: 3075868.5099 - mean_squared_error: 3075868.5099 - val_loss: 2992714.7820 - val_mean_squared_error: 2992714.7820
Epoch 31/250
- 0s - loss: 3011537.2513 - mean_squared_error: 3011537.2513 - val_loss: 2916240.5889 - val_mean_squared_error: 2916240.5889
Epoch 32/250
- 0s - loss: 2950834.9374 - mean_squared_error: 2950834.9374 - val_loss: 2853476.3283 - val_mean_squared_error: 2853476.3283
Epoch 33/250
- 0s - loss: 2896146.2107 - mean_squared_error: 2896146.2107 - val_loss: 2797956.3931 - val_mean_squared_error: 2797956.3931
Epoch 34/250
- 0s - loss: 2845359.1844 - mean_squared_error: 2845359.1844 - val_loss: 2756268.6799 - val_mean_squared_error: 2756268.6799
Epoch 35/250
- 0s - loss: 2799651.4802 - mean_squared_error: 2799651.4802 - val_loss: 2696497.8046 - val_mean_squared_error: 2696497.8046
Epoch 36/250
- 0s - loss: 2756932.6045 - mean_squared_error: 2756932.6045 - val_loss: 2652229.5122 - val_mean_squared_error: 2652229.5122
Epoch 37/250
- 0s - loss: 2718146.0056 - mean_squared_error: 2718146.0056 - val_loss: 2610052.9367 - val_mean_squared_error: 2610052.9367
Epoch 38/250
- 0s - loss: 2681826.8783 - mean_squared_error: 2681826.8783 - val_loss: 2576333.5379 - val_mean_squared_error: 2576333.5379
Epoch 39/250
- 0s - loss: 2646768.1726 - mean_squared_error: 2646768.1726 - val_loss: 2535503.5141 - val_mean_squared_error: 2535503.5141
Epoch 40/250
- 0s - loss: 2614777.8154 - mean_squared_error: 2614777.8154 - val_loss: 2503085.7453 - val_mean_squared_error: 2503085.7453
Epoch 41/250
- 0s - loss: 2585534.7258 - mean_squared_error: 2585534.7258 - val_loss: 2473390.2650 - val_mean_squared_error: 2473390.2650
Epoch 42/250
- 0s - loss: 2560146.6899 - mean_squared_error: 2560146.6899 - val_loss: 2444374.3726 - val_mean_squared_error: 2444374.3726
Epoch 43/250
- 0s - loss: 2532669.1185 - mean_squared_error: 2532669.1185 - val_loss: 2418029.5618 - val_mean_squared_error: 2418029.5618
Epoch 44/250
- 0s - loss: 2509591.7315 - mean_squared_error: 2509591.7315 - val_loss: 2393902.2946 - val_mean_squared_error: 2393902.2946
Epoch 45/250
- 0s - loss: 2485903.8244 - mean_squared_error: 2485903.8244 - val_loss: 2374926.1074 - val_mean_squared_error: 2374926.1074
Epoch 46/250
- 0s - loss: 2468145.9276 - mean_squared_error: 2468145.9276 - val_loss: 2353132.2925 - val_mean_squared_error: 2353132.2925
Epoch 47/250
- 0s - loss: 2449389.6913 - mean_squared_error: 2449389.6913 - val_loss: 2330850.7967 - val_mean_squared_error: 2330850.7967
Epoch 48/250
- 0s - loss: 2430694.4924 - mean_squared_error: 2430694.4924 - val_loss: 2315977.1396 - val_mean_squared_error: 2315977.1396
Epoch 49/250
- 0s - loss: 2416348.0670 - mean_squared_error: 2416348.0670 - val_loss: 2295317.3459 - val_mean_squared_error: 2295317.3459
Epoch 50/250
- 0s - loss: 2400174.9707 - mean_squared_error: 2400174.9707 - val_loss: 2280247.3585 - val_mean_squared_error: 2280247.3585
Epoch 51/250
- 0s - loss: 2386847.7805 - mean_squared_error: 2386847.7805 - val_loss: 2269282.1988 - val_mean_squared_error: 2269282.1988
Epoch 52/250
- 0s - loss: 2373865.5490 - mean_squared_error: 2373865.5490 - val_loss: 2253546.8710 - val_mean_squared_error: 2253546.8710
Epoch 53/250
- 0s - loss: 2362687.3404 - mean_squared_error: 2362687.3404 - val_loss: 2241699.1739 - val_mean_squared_error: 2241699.1739
Epoch 54/250
- 0s - loss: 2350158.3027 - mean_squared_error: 2350158.3027 - val_loss: 2229586.8293 - val_mean_squared_error: 2229586.8293
Epoch 55/250
- 0s - loss: 2340199.4378 - mean_squared_error: 2340199.4378 - val_loss: 2223216.2266 - val_mean_squared_error: 2223216.2266
Epoch 56/250
- 0s - loss: 2328815.8881 - mean_squared_error: 2328815.8881 - val_loss: 2215892.9633 - val_mean_squared_error: 2215892.9633
Epoch 57/250
- 0s - loss: 2319769.2307 - mean_squared_error: 2319769.2307 - val_loss: 2202649.4680 - val_mean_squared_error: 2202649.4680
Epoch 58/250
- 0s - loss: 2311106.1876 - mean_squared_error: 2311106.1876 - val_loss: 2190911.9708 - val_mean_squared_error: 2190911.9708
Epoch 59/250
- 0s - loss: 2303140.6940 - mean_squared_error: 2303140.6940 - val_loss: 2190453.6531 - val_mean_squared_error: 2190453.6531
Epoch 60/250
- 0s - loss: 2295309.2408 - mean_squared_error: 2295309.2408 - val_loss: 2173813.5528 - val_mean_squared_error: 2173813.5528
Epoch 61/250
- 0s - loss: 2286456.1451 - mean_squared_error: 2286456.1451 - val_loss: 2167401.4068 - val_mean_squared_error: 2167401.4068
Epoch 62/250
- 0s - loss: 2278925.0642 - mean_squared_error: 2278925.0642 - val_loss: 2158559.3234 - val_mean_squared_error: 2158559.3234
Epoch 63/250
- 0s - loss: 2272597.3724 - mean_squared_error: 2272597.3724 - val_loss: 2151993.7547 - val_mean_squared_error: 2151993.7547
Epoch 64/250
- 0s - loss: 2265358.6924 - mean_squared_error: 2265358.6924 - val_loss: 2146581.5500 - val_mean_squared_error: 2146581.5500
Epoch 65/250
- 0s - loss: 2259204.1708 - mean_squared_error: 2259204.1708 - val_loss: 2138775.9063 - val_mean_squared_error: 2138775.9063
Epoch 66/250
- 0s - loss: 2251698.1355 - mean_squared_error: 2251698.1355 - val_loss: 2132688.4142 - val_mean_squared_error: 2132688.4142
Epoch 67/250
- 0s - loss: 2245842.9347 - mean_squared_error: 2245842.9347 - val_loss: 2127250.3298 - val_mean_squared_error: 2127250.3298
Epoch 68/250
- 0s - loss: 2239787.1670 - mean_squared_error: 2239787.1670 - val_loss: 2128124.5670 - val_mean_squared_error: 2128124.5670
Epoch 69/250
- 0s - loss: 2233091.2950 - mean_squared_error: 2233091.2950 - val_loss: 2120944.2249 - val_mean_squared_error: 2120944.2249
Epoch 70/250
- 0s - loss: 2227085.7098 - mean_squared_error: 2227085.7098 - val_loss: 2114163.3953 - val_mean_squared_error: 2114163.3953
Epoch 71/250
- 0s - loss: 2220383.1575 - mean_squared_error: 2220383.1575 - val_loss: 2119813.9272 - val_mean_squared_error: 2119813.9272
Epoch 72/250
- 0s - loss: 2215016.5886 - mean_squared_error: 2215016.5886 - val_loss: 2098265.5178 - val_mean_squared_error: 2098265.5178
Epoch 73/250
- 0s - loss: 2209031.0828 - mean_squared_error: 2209031.0828 - val_loss: 2093349.4299 - val_mean_squared_error: 2093349.4299
Epoch 74/250
- 0s - loss: 2203458.1824 - mean_squared_error: 2203458.1824 - val_loss: 2087530.1435 - val_mean_squared_error: 2087530.1435
Epoch 75/250
- 0s - loss: 2197507.4423 - mean_squared_error: 2197507.4423 - val_loss: 2084310.7636 - val_mean_squared_error: 2084310.7636
Epoch 76/250
- 0s - loss: 2191870.9516 - mean_squared_error: 2191870.9516 - val_loss: 2078751.1230 - val_mean_squared_error: 2078751.1230
Epoch 77/250
- 0s - loss: 2186590.2370 - mean_squared_error: 2186590.2370 - val_loss: 2073632.4209 - val_mean_squared_error: 2073632.4209
Epoch 78/250
- 0s - loss: 2180675.0755 - mean_squared_error: 2180675.0755 - val_loss: 2067455.0566 - val_mean_squared_error: 2067455.0566
Epoch 79/250
- 0s - loss: 2175871.8791 - mean_squared_error: 2175871.8791 - val_loss: 2062080.2746 - val_mean_squared_error: 2062080.2746
Epoch 80/250
- 0s - loss: 2170960.8270 - mean_squared_error: 2170960.8270 - val_loss: 2076134.0571 - val_mean_squared_error: 2076134.0571
Epoch 81/250
- 0s - loss: 2165095.7891 - mean_squared_error: 2165095.7891 - val_loss: 2060063.3091 - val_mean_squared_error: 2060063.3091
Epoch 82/250
- 0s - loss: 2159210.9014 - mean_squared_error: 2159210.9014 - val_loss: 2054764.6278 - val_mean_squared_error: 2054764.6278
Epoch 83/250
- 0s - loss: 2154804.6965 - mean_squared_error: 2154804.6965 - val_loss: 2042656.1980 - val_mean_squared_error: 2042656.1980
Epoch 84/250
- 0s - loss: 2151000.8027 - mean_squared_error: 2151000.8027 - val_loss: 2041542.0261 - val_mean_squared_error: 2041542.0261
Epoch 85/250
- 0s - loss: 2144402.9209 - mean_squared_error: 2144402.9209 - val_loss: 2034710.8433 - val_mean_squared_error: 2034710.8433
Epoch 86/250
- 0s - loss: 2139382.6877 - mean_squared_error: 2139382.6877 - val_loss: 2029521.7206 - val_mean_squared_error: 2029521.7206
Epoch 87/250
- 0s - loss: 2134508.9045 - mean_squared_error: 2134508.9045 - val_loss: 2025544.5526 - val_mean_squared_error: 2025544.5526
Epoch 88/250
- 0s - loss: 2130530.0560 - mean_squared_error: 2130530.0560 - val_loss: 2020708.7063 - val_mean_squared_error: 2020708.7063
Epoch 89/250
- 0s - loss: 2124692.8997 - mean_squared_error: 2124692.8997 - val_loss: 2016661.2367 - val_mean_squared_error: 2016661.2367
Epoch 90/250
- 0s - loss: 2119100.6322 - mean_squared_error: 2119100.6322 - val_loss: 2024581.7835 - val_mean_squared_error: 2024581.7835
Epoch 91/250
- 0s - loss: 2115483.7229 - mean_squared_error: 2115483.7229 - val_loss: 2008754.8749 - val_mean_squared_error: 2008754.8749
Epoch 92/250
- 0s - loss: 2110360.7427 - mean_squared_error: 2110360.7427 - val_loss: 2007724.7695 - val_mean_squared_error: 2007724.7695
Epoch 93/250
- 0s - loss: 2104714.5825 - mean_squared_error: 2104714.5825 - val_loss: 2008926.0319 - val_mean_squared_error: 2008926.0319
Epoch 94/250
- 0s - loss: 2100296.9009 - mean_squared_error: 2100296.9009 - val_loss: 1995537.1630 - val_mean_squared_error: 1995537.1630
Epoch 95/250
- 0s - loss: 2095775.2807 - mean_squared_error: 2095775.2807 - val_loss: 1998770.4627 - val_mean_squared_error: 1998770.4627
Epoch 96/250
- 0s - loss: 2090610.8210 - mean_squared_error: 2090610.8210 - val_loss: 1991205.4927 - val_mean_squared_error: 1991205.4927
Epoch 97/250
- 0s - loss: 2085764.6586 - mean_squared_error: 2085764.6586 - val_loss: 1982456.1479 - val_mean_squared_error: 1982456.1479
Epoch 98/250
- 0s - loss: 2081778.4795 - mean_squared_error: 2081778.4795 - val_loss: 1984038.7297 - val_mean_squared_error: 1984038.7297
Epoch 99/250
- 0s - loss: 2076921.0596 - mean_squared_error: 2076921.0596 - val_loss: 1974410.2433 - val_mean_squared_error: 1974410.2433
Epoch 100/250
- 0s - loss: 2071642.4116 - mean_squared_error: 2071642.4116 - val_loss: 1970844.3068 - val_mean_squared_error: 1970844.3068
Epoch 101/250
- 0s - loss: 2067992.1074 - mean_squared_error: 2067992.1074 - val_loss: 1966067.1146 - val_mean_squared_error: 1966067.1146
Epoch 102/250
- 0s - loss: 2062705.6920 - mean_squared_error: 2062705.6920 - val_loss: 1964978.2044 - val_mean_squared_error: 1964978.2044
Epoch 103/250
- 1s - loss: 2058635.8663 - mean_squared_error: 2058635.8663 - val_loss: 1960653.1206 - val_mean_squared_error: 1960653.1206
Epoch 104/250
- 1s - loss: 2053453.2750 - mean_squared_error: 2053453.2750 - val_loss: 1956940.2522 - val_mean_squared_error: 1956940.2522
Epoch 105/250
- 0s - loss: 2049969.1384 - mean_squared_error: 2049969.1384 - val_loss: 1950447.4171 - val_mean_squared_error: 1950447.4171
Epoch 106/250
- 0s - loss: 2044646.2613 - mean_squared_error: 2044646.2613 - val_loss: 1946335.1700 - val_mean_squared_error: 1946335.1700
Epoch 107/250
- 0s - loss: 2040847.5135 - mean_squared_error: 2040847.5135 - val_loss: 1950765.8945 - val_mean_squared_error: 1950765.8945
Epoch 108/250
- 0s - loss: 2035333.6843 - mean_squared_error: 2035333.6843 - val_loss: 1943112.7308 - val_mean_squared_error: 1943112.7308
Epoch 109/250
- 0s - loss: 2031570.0148 - mean_squared_error: 2031570.0148 - val_loss: 1937313.6635 - val_mean_squared_error: 1937313.6635
Epoch 110/250
- 0s - loss: 2026515.8787 - mean_squared_error: 2026515.8787 - val_loss: 1930995.4182 - val_mean_squared_error: 1930995.4182
Epoch 111/250
- 0s - loss: 2023262.6958 - mean_squared_error: 2023262.6958 - val_loss: 1926765.3571 - val_mean_squared_error: 1926765.3571
Epoch 112/250
- 0s - loss: 2018275.2594 - mean_squared_error: 2018275.2594 - val_loss: 1923056.6220 - val_mean_squared_error: 1923056.6220
Epoch 113/250
- 0s - loss: 2013793.3882 - mean_squared_error: 2013793.3882 - val_loss: 1920843.6845 - val_mean_squared_error: 1920843.6845
Epoch 114/250
- 0s - loss: 2009802.3657 - mean_squared_error: 2009802.3657 - val_loss: 1916405.0942 - val_mean_squared_error: 1916405.0942
Epoch 115/250
- 0s - loss: 2005557.3843 - mean_squared_error: 2005557.3843 - val_loss: 1920216.2247 - val_mean_squared_error: 1920216.2247
Epoch 116/250
- 0s - loss: 2000834.9872 - mean_squared_error: 2000834.9872 - val_loss: 1913231.6625 - val_mean_squared_error: 1913231.6625
Epoch 117/250
- 0s - loss: 1996924.4391 - mean_squared_error: 1996924.4391 - val_loss: 1905361.8010 - val_mean_squared_error: 1905361.8010
Epoch 118/250
- 0s - loss: 1991738.4791 - mean_squared_error: 1991738.4791 - val_loss: 1901166.0414 - val_mean_squared_error: 1901166.0414
Epoch 119/250
- 0s - loss: 1987464.5905 - mean_squared_error: 1987464.5905 - val_loss: 1900646.9869 - val_mean_squared_error: 1900646.9869
Epoch 120/250
- 0s - loss: 1982866.4694 - mean_squared_error: 1982866.4694 - val_loss: 1896726.6348 - val_mean_squared_error: 1896726.6348
Epoch 121/250
- 0s - loss: 1979190.1764 - mean_squared_error: 1979190.1764 - val_loss: 1889626.5674 - val_mean_squared_error: 1889626.5674
Epoch 122/250
- 0s - loss: 1974747.3787 - mean_squared_error: 1974747.3787 - val_loss: 1889790.7669 - val_mean_squared_error: 1889790.7669
Epoch 123/250
- 0s - loss: 1970600.7402 - mean_squared_error: 1970600.7402 - val_loss: 1881613.5393 - val_mean_squared_error: 1881613.5393
Epoch 124/250
- 0s - loss: 1966440.0516 - mean_squared_error: 1966440.0516 - val_loss: 1881952.2009 - val_mean_squared_error: 1881952.2009
Epoch 125/250
- 0s - loss: 1963144.5010 - mean_squared_error: 1963144.5010 - val_loss: 1874578.3827 - val_mean_squared_error: 1874578.3827
Epoch 126/250
- 0s - loss: 1958002.3114 - mean_squared_error: 1958002.3114 - val_loss: 1881907.8777 - val_mean_squared_error: 1881907.8777
Epoch 127/250
- 0s - loss: 1953781.4717 - mean_squared_error: 1953781.4717 - val_loss: 1866496.5014 - val_mean_squared_error: 1866496.5014
Epoch 128/250
- 0s - loss: 1949579.8435 - mean_squared_error: 1949579.8435 - val_loss: 1862999.9314 - val_mean_squared_error: 1862999.9314
Epoch 129/250
- 0s - loss: 1944837.7633 - mean_squared_error: 1944837.7633 - val_loss: 1859692.0708 - val_mean_squared_error: 1859692.0708
Epoch 130/250
- 0s - loss: 1941181.8801 - mean_squared_error: 1941181.8801 - val_loss: 1870401.3512 - val_mean_squared_error: 1870401.3512
Epoch 131/250
- 0s - loss: 1937206.9816 - mean_squared_error: 1937206.9816 - val_loss: 1855640.7789 - val_mean_squared_error: 1855640.7789
Epoch 132/250
- 1s - loss: 1932482.7280 - mean_squared_error: 1932482.7280 - val_loss: 1853098.5790 - val_mean_squared_error: 1853098.5790
Epoch 133/250
- 1s - loss: 1928831.6393 - mean_squared_error: 1928831.6393 - val_loss: 1845656.8632 - val_mean_squared_error: 1845656.8632
Epoch 134/250
- 0s - loss: 1923718.3025 - mean_squared_error: 1923718.3025 - val_loss: 1841296.4944 - val_mean_squared_error: 1841296.4944
Epoch 135/250
- 0s - loss: 1919285.1301 - mean_squared_error: 1919285.1301 - val_loss: 1839304.6138 - val_mean_squared_error: 1839304.6138
Epoch 136/250
- 0s - loss: 1915512.9725 - mean_squared_error: 1915512.9725 - val_loss: 1833941.8848 - val_mean_squared_error: 1833941.8848
Epoch 137/250
- 0s - loss: 1910338.2096 - mean_squared_error: 1910338.2096 - val_loss: 1829266.4789 - val_mean_squared_error: 1829266.4789
Epoch 138/250
- 0s - loss: 1906807.1133 - mean_squared_error: 1906807.1133 - val_loss: 1826667.6707 - val_mean_squared_error: 1826667.6707
Epoch 139/250
- 0s - loss: 1901958.9682 - mean_squared_error: 1901958.9682 - val_loss: 1822769.3903 - val_mean_squared_error: 1822769.3903
Epoch 140/250
- 0s - loss: 1898180.0895 - mean_squared_error: 1898180.0895 - val_loss: 1818848.6565 - val_mean_squared_error: 1818848.6565
Epoch 141/250
- 0s - loss: 1893384.4182 - mean_squared_error: 1893384.4182 - val_loss: 1825904.4577 - val_mean_squared_error: 1825904.4577
Epoch 142/250
- 0s - loss: 1888857.0500 - mean_squared_error: 1888857.0500 - val_loss: 1812047.4093 - val_mean_squared_error: 1812047.4093
Epoch 143/250
- 0s - loss: 1885649.5577 - mean_squared_error: 1885649.5577 - val_loss: 1815988.5720 - val_mean_squared_error: 1815988.5720
Epoch 144/250
- 0s - loss: 1882728.8948 - mean_squared_error: 1882728.8948 - val_loss: 1804221.2971 - val_mean_squared_error: 1804221.2971
Epoch 145/250
- 0s - loss: 1878070.7728 - mean_squared_error: 1878070.7728 - val_loss: 1800390.6373 - val_mean_squared_error: 1800390.6373
Epoch 146/250
- 0s - loss: 1873359.5868 - mean_squared_error: 1873359.5868 - val_loss: 1796718.0096 - val_mean_squared_error: 1796718.0096
Epoch 147/250
- 0s - loss: 1870450.4402 - mean_squared_error: 1870450.4402 - val_loss: 1793502.3480 - val_mean_squared_error: 1793502.3480
Epoch 148/250
- 0s - loss: 1864935.4132 - mean_squared_error: 1864935.4132 - val_loss: 1790719.0737 - val_mean_squared_error: 1790719.0737
Epoch 149/250
- 0s - loss: 1860335.5980 - mean_squared_error: 1860335.5980 - val_loss: 1787109.7601 - val_mean_squared_error: 1787109.7601
Epoch 150/250
- 0s - loss: 1857528.6761 - mean_squared_error: 1857528.6761 - val_loss: 1782251.8564 - val_mean_squared_error: 1782251.8564
Epoch 151/250
- 0s - loss: 1853086.1135 - mean_squared_error: 1853086.1135 - val_loss: 1779972.3222 - val_mean_squared_error: 1779972.3222
Epoch 152/250
- 0s - loss: 1849172.5880 - mean_squared_error: 1849172.5880 - val_loss: 1775980.5159 - val_mean_squared_error: 1775980.5159
Epoch 153/250
- 0s - loss: 1844933.4104 - mean_squared_error: 1844933.4104 - val_loss: 1771529.7060 - val_mean_squared_error: 1771529.7060
Epoch 154/250
- 0s - loss: 1839683.2720 - mean_squared_error: 1839683.2720 - val_loss: 1767939.3851 - val_mean_squared_error: 1767939.3851
Epoch 155/250
- 0s - loss: 1836064.3526 - mean_squared_error: 1836064.3526 - val_loss: 1764414.1924 - val_mean_squared_error: 1764414.1924
Epoch 156/250
- 0s - loss: 1832377.5910 - mean_squared_error: 1832377.5910 - val_loss: 1761295.6983 - val_mean_squared_error: 1761295.6983
Epoch 157/250
- 0s - loss: 1828378.2116 - mean_squared_error: 1828378.2116 - val_loss: 1756511.1158 - val_mean_squared_error: 1756511.1158
Epoch 158/250
- 0s - loss: 1824890.7548 - mean_squared_error: 1824890.7548 - val_loss: 1754338.1330 - val_mean_squared_error: 1754338.1330
Epoch 159/250
- 0s - loss: 1820081.3972 - mean_squared_error: 1820081.3972 - val_loss: 1751247.4256 - val_mean_squared_error: 1751247.4256
Epoch 160/250
- 0s - loss: 1816636.5487 - mean_squared_error: 1816636.5487 - val_loss: 1756630.1609 - val_mean_squared_error: 1756630.1609
Epoch 161/250
- 0s - loss: 1811579.5376 - mean_squared_error: 1811579.5376 - val_loss: 1743509.7337 - val_mean_squared_error: 1743509.7337
Epoch 162/250
- 0s - loss: 1807536.9920 - mean_squared_error: 1807536.9920 - val_loss: 1742150.8448 - val_mean_squared_error: 1742150.8448
Epoch 163/250
- 0s - loss: 1803971.9994 - mean_squared_error: 1803971.9994 - val_loss: 1736175.7619 - val_mean_squared_error: 1736175.7619
Epoch 164/250
- 0s - loss: 1800349.7850 - mean_squared_error: 1800349.7850 - val_loss: 1743091.8461 - val_mean_squared_error: 1743091.8461
Epoch 165/250
- 0s - loss: 1794217.3592 - mean_squared_error: 1794217.3592 - val_loss: 1727758.6505 - val_mean_squared_error: 1727758.6505
Epoch 166/250
- 0s - loss: 1791519.7027 - mean_squared_error: 1791519.7027 - val_loss: 1749954.5221 - val_mean_squared_error: 1749954.5221
Epoch 167/250
- 0s - loss: 1789118.2473 - mean_squared_error: 1789118.2473 - val_loss: 1721773.4305 - val_mean_squared_error: 1721773.4305
Epoch 168/250
- 0s - loss: 1784228.6996 - mean_squared_error: 1784228.6996 - val_loss: 1717498.3095 - val_mean_squared_error: 1717498.3095
Epoch 169/250
- 0s - loss: 1779127.8237 - mean_squared_error: 1779127.8237 - val_loss: 1713949.0157 - val_mean_squared_error: 1713949.0157
Epoch 170/250
- 0s - loss: 1775922.7718 - mean_squared_error: 1775922.7718 - val_loss: 1711449.6809 - val_mean_squared_error: 1711449.6809
Epoch 171/250
- 0s - loss: 1771560.6863 - mean_squared_error: 1771560.6863 - val_loss: 1709218.2926 - val_mean_squared_error: 1709218.2926
Epoch 172/250
- 0s - loss: 1768529.1427 - mean_squared_error: 1768529.1427 - val_loss: 1706059.7845 - val_mean_squared_error: 1706059.7845
Epoch 173/250
- 0s - loss: 1764611.6279 - mean_squared_error: 1764611.6279 - val_loss: 1704987.3673 - val_mean_squared_error: 1704987.3673
Epoch 174/250
- 0s - loss: 1759797.3488 - mean_squared_error: 1759797.3488 - val_loss: 1696676.8063 - val_mean_squared_error: 1696676.8063
Epoch 175/250
- 0s - loss: 1756353.1683 - mean_squared_error: 1756353.1683 - val_loss: 1693596.5106 - val_mean_squared_error: 1693596.5106
Epoch 176/250
- 0s - loss: 1752005.8658 - mean_squared_error: 1752005.8658 - val_loss: 1689543.5374 - val_mean_squared_error: 1689543.5374
Epoch 177/250
- 0s - loss: 1747951.0195 - mean_squared_error: 1747951.0195 - val_loss: 1686419.0251 - val_mean_squared_error: 1686419.0251
Epoch 178/250
- 0s - loss: 1744804.0021 - mean_squared_error: 1744804.0021 - val_loss: 1682881.5861 - val_mean_squared_error: 1682881.5861
Epoch 179/250
- 0s - loss: 1741434.6224 - mean_squared_error: 1741434.6224 - val_loss: 1691390.7072 - val_mean_squared_error: 1691390.7072
Epoch 180/250
- 0s - loss: 1737770.1080 - mean_squared_error: 1737770.1080 - val_loss: 1675420.7468 - val_mean_squared_error: 1675420.7468
Epoch 181/250
- 0s - loss: 1732393.8311 - mean_squared_error: 1732393.8311 - val_loss: 1675718.3392 - val_mean_squared_error: 1675718.3392
Epoch 182/250
- 0s - loss: 1728406.2045 - mean_squared_error: 1728406.2045 - val_loss: 1668087.5327 - val_mean_squared_error: 1668087.5327
Epoch 183/250
- 0s - loss: 1724420.8879 - mean_squared_error: 1724420.8879 - val_loss: 1664868.2181 - val_mean_squared_error: 1664868.2181
Epoch 184/250
- 0s - loss: 1720156.1015 - mean_squared_error: 1720156.1015 - val_loss: 1669234.7821 - val_mean_squared_error: 1669234.7821
Epoch 185/250
- 0s - loss: 1716196.7695 - mean_squared_error: 1716196.7695 - val_loss: 1669442.6978 - val_mean_squared_error: 1669442.6978
Epoch 186/250
- 0s - loss: 1712488.4788 - mean_squared_error: 1712488.4788 - val_loss: 1653888.1396 - val_mean_squared_error: 1653888.1396
Epoch 187/250
- 0s - loss: 1708032.9664 - mean_squared_error: 1708032.9664 - val_loss: 1650641.3101 - val_mean_squared_error: 1650641.3101
Epoch 188/250
- 0s - loss: 1704076.8909 - mean_squared_error: 1704076.8909 - val_loss: 1647999.1042 - val_mean_squared_error: 1647999.1042
Epoch 189/250
- 0s - loss: 1701110.1930 - mean_squared_error: 1701110.1930 - val_loss: 1646898.5643 - val_mean_squared_error: 1646898.5643
Epoch 190/250
- 0s - loss: 1697091.7084 - mean_squared_error: 1697091.7084 - val_loss: 1642208.3946 - val_mean_squared_error: 1642208.3946
Epoch 191/250
- 0s - loss: 1693360.1219 - mean_squared_error: 1693360.1219 - val_loss: 1636948.2817 - val_mean_squared_error: 1636948.2817
Epoch 192/250
- 0s - loss: 1689616.1710 - mean_squared_error: 1689616.1710 - val_loss: 1634705.0452 - val_mean_squared_error: 1634705.0452
Epoch 193/250
- 0s - loss: 1685067.2261 - mean_squared_error: 1685067.2261 - val_loss: 1630226.0061 - val_mean_squared_error: 1630226.0061
Epoch 194/250
- 0s - loss: 1681237.7659 - mean_squared_error: 1681237.7659 - val_loss: 1639004.3018 - val_mean_squared_error: 1639004.3018
Epoch 195/250
- 0s - loss: 1678298.5193 - mean_squared_error: 1678298.5193 - val_loss: 1623961.1689 - val_mean_squared_error: 1623961.1689
Epoch 196/250
- 0s - loss: 1673192.0288 - mean_squared_error: 1673192.0288 - val_loss: 1619567.3824 - val_mean_squared_error: 1619567.3824
Epoch 197/250
- 0s - loss: 1669092.1021 - mean_squared_error: 1669092.1021 - val_loss: 1619046.1713 - val_mean_squared_error: 1619046.1713
Epoch 198/250
- 0s - loss: 1664606.5096 - mean_squared_error: 1664606.5096 - val_loss: 1615387.4159 - val_mean_squared_error: 1615387.4159
Epoch 199/250
- 0s - loss: 1662564.2851 - mean_squared_error: 1662564.2851 - val_loss: 1609142.0948 - val_mean_squared_error: 1609142.0948
Epoch 200/250
- 0s - loss: 1657685.3866 - mean_squared_error: 1657685.3866 - val_loss: 1605894.4098 - val_mean_squared_error: 1605894.4098
Epoch 201/250
- 0s - loss: 1654749.7125 - mean_squared_error: 1654749.7125 - val_loss: 1606032.8303 - val_mean_squared_error: 1606032.8303
Epoch 202/250
- 0s - loss: 1649906.3164 - mean_squared_error: 1649906.3164 - val_loss: 1598597.9039 - val_mean_squared_error: 1598597.9039
Epoch 203/250
- 0s - loss: 1646614.9474 - mean_squared_error: 1646614.9474 - val_loss: 1600799.1936 - val_mean_squared_error: 1600799.1936
Epoch 204/250
- 0s - loss: 1643058.2099 - mean_squared_error: 1643058.2099 - val_loss: 1596763.3237 - val_mean_squared_error: 1596763.3237
Epoch 205/250
- 0s - loss: 1638300.3648 - mean_squared_error: 1638300.3648 - val_loss: 1593418.9744 - val_mean_squared_error: 1593418.9744
Epoch 206/250
- 0s - loss: 1634605.7919 - mean_squared_error: 1634605.7919 - val_loss: 1591944.4761 - val_mean_squared_error: 1591944.4761
Epoch 207/250
- 0s - loss: 1632396.7522 - mean_squared_error: 1632396.7522 - val_loss: 1594654.7668 - val_mean_squared_error: 1594654.7668
Epoch 208/250
- 0s - loss: 1626509.9061 - mean_squared_error: 1626509.9061 - val_loss: 1581620.4115 - val_mean_squared_error: 1581620.4115
Epoch 209/250
- 0s - loss: 1623937.1295 - mean_squared_error: 1623937.1295 - val_loss: 1579898.4873 - val_mean_squared_error: 1579898.4873
Epoch 210/250
- 0s - loss: 1621066.5514 - mean_squared_error: 1621066.5514 - val_loss: 1571717.8550 - val_mean_squared_error: 1571717.8550
Epoch 211/250
- 0s - loss: 1616139.5395 - mean_squared_error: 1616139.5395 - val_loss: 1569710.2550 - val_mean_squared_error: 1569710.2550
Epoch 212/250
- 0s - loss: 1612243.5690 - mean_squared_error: 1612243.5690 - val_loss: 1567843.0187 - val_mean_squared_error: 1567843.0187
Epoch 213/250
- 0s - loss: 1609260.8194 - mean_squared_error: 1609260.8194 - val_loss: 1572308.2530 - val_mean_squared_error: 1572308.2530
Epoch 214/250
- 0s - loss: 1605613.5753 - mean_squared_error: 1605613.5753 - val_loss: 1557996.3463 - val_mean_squared_error: 1557996.3463
Epoch 215/250
- 0s - loss: 1600952.7402 - mean_squared_error: 1600952.7402 - val_loss: 1555764.3567 - val_mean_squared_error: 1555764.3567
Epoch 216/250
- 0s - loss: 1597516.2842 - mean_squared_error: 1597516.2842 - val_loss: 1552335.2397 - val_mean_squared_error: 1552335.2397
Epoch 217/250
- 0s - loss: 1595406.1265 - mean_squared_error: 1595406.1265 - val_loss: 1548897.1456 - val_mean_squared_error: 1548897.1456
Epoch 218/250
- 0s - loss: 1591035.0155 - mean_squared_error: 1591035.0155 - val_loss: 1546232.4290 - val_mean_squared_error: 1546232.4290
Epoch 219/250
- 0s - loss: 1587376.0179 - mean_squared_error: 1587376.0179 - val_loss: 1541615.9383 - val_mean_squared_error: 1541615.9383
Epoch 220/250
- 0s - loss: 1583196.2946 - mean_squared_error: 1583196.2946 - val_loss: 1539573.1838 - val_mean_squared_error: 1539573.1838
Epoch 221/250
- 0s - loss: 1580048.1778 - mean_squared_error: 1580048.1778 - val_loss: 1539254.7977 - val_mean_squared_error: 1539254.7977
Epoch 222/250
- 0s - loss: 1576428.4779 - mean_squared_error: 1576428.4779 - val_loss: 1537425.3814 - val_mean_squared_error: 1537425.3814
Epoch 223/250
- 0s - loss: 1571698.2321 - mean_squared_error: 1571698.2321 - val_loss: 1533045.4937 - val_mean_squared_error: 1533045.4937
Epoch 224/250
- 1s - loss: 1569309.8116 - mean_squared_error: 1569309.8116 - val_loss: 1524448.8505 - val_mean_squared_error: 1524448.8505
Epoch 225/250
- 0s - loss: 1565261.5082 - mean_squared_error: 1565261.5082 - val_loss: 1521244.5449 - val_mean_squared_error: 1521244.5449
Epoch 226/250
- 0s - loss: 1561696.2988 - mean_squared_error: 1561696.2988 - val_loss: 1521136.5315 - val_mean_squared_error: 1521136.5315
Epoch 227/250
- 0s - loss: 1557760.5976 - mean_squared_error: 1557760.5976 - val_loss: 1514913.8519 - val_mean_squared_error: 1514913.8519
Epoch 228/250
- 0s - loss: 1554509.0372 - mean_squared_error: 1554509.0372 - val_loss: 1511611.5119 - val_mean_squared_error: 1511611.5119
Epoch 229/250
- 0s - loss: 1550976.7215 - mean_squared_error: 1550976.7215 - val_loss: 1509094.8388 - val_mean_squared_error: 1509094.8388
Epoch 230/250
- 0s - loss: 1546977.6634 - mean_squared_error: 1546977.6634 - val_loss: 1505029.9383 - val_mean_squared_error: 1505029.9383
Epoch 231/250
- 0s - loss: 1543970.9746 - mean_squared_error: 1543970.9746 - val_loss: 1502910.6582 - val_mean_squared_error: 1502910.6582
Epoch 232/250
- 0s - loss: 1540305.0970 - mean_squared_error: 1540305.0970 - val_loss: 1498495.6655 - val_mean_squared_error: 1498495.6655
Epoch 233/250
- 0s - loss: 1537501.6374 - mean_squared_error: 1537501.6374 - val_loss: 1495304.1388 - val_mean_squared_error: 1495304.1388
Epoch 234/250
- 0s - loss: 1533388.2508 - mean_squared_error: 1533388.2508 - val_loss: 1492806.1005 - val_mean_squared_error: 1492806.1005
Epoch 235/250
- 0s - loss: 1530941.4702 - mean_squared_error: 1530941.4702 - val_loss: 1499393.1403 - val_mean_squared_error: 1499393.1403
Epoch 236/250
- 0s - loss: 1526883.5424 - mean_squared_error: 1526883.5424 - val_loss: 1490247.0621 - val_mean_squared_error: 1490247.0621
Epoch 237/250
- 0s - loss: 1524231.6881 - mean_squared_error: 1524231.6881 - val_loss: 1493653.0241 - val_mean_squared_error: 1493653.0241
Epoch 238/250
- 0s - loss: 1519628.2648 - mean_squared_error: 1519628.2648 - val_loss: 1482725.0214 - val_mean_squared_error: 1482725.0214
Epoch 239/250
- 0s - loss: 1517536.3750 - mean_squared_error: 1517536.3750 - val_loss: 1476558.6559 - val_mean_squared_error: 1476558.6559
Epoch 240/250
- 0s - loss: 1514165.7144 - mean_squared_error: 1514165.7144 - val_loss: 1475985.6456 - val_mean_squared_error: 1475985.6456
Epoch 241/250
- 0s - loss: 1510455.2794 - mean_squared_error: 1510455.2794 - val_loss: 1470677.5349 - val_mean_squared_error: 1470677.5349
Epoch 242/250
- 0s - loss: 1508992.9663 - mean_squared_error: 1508992.9663 - val_loss: 1474781.7924 - val_mean_squared_error: 1474781.7924
Epoch 243/250
- 0s - loss: 1503767.5517 - mean_squared_error: 1503767.5517 - val_loss: 1465611.5074 - val_mean_squared_error: 1465611.5074
Epoch 244/250
- 0s - loss: 1501195.4531 - mean_squared_error: 1501195.4531 - val_loss: 1464832.4664 - val_mean_squared_error: 1464832.4664
Epoch 245/250
- 0s - loss: 1497824.0992 - mean_squared_error: 1497824.0992 - val_loss: 1462425.5150 - val_mean_squared_error: 1462425.5150
Epoch 246/250
- 0s - loss: 1495264.5258 - mean_squared_error: 1495264.5258 - val_loss: 1459882.0771 - val_mean_squared_error: 1459882.0771
Epoch 247/250
- 0s - loss: 1493924.6338 - mean_squared_error: 1493924.6338 - val_loss: 1454529.6073 - val_mean_squared_error: 1454529.6073
Epoch 248/250
- 0s - loss: 1489410.9016 - mean_squared_error: 1489410.9016 - val_loss: 1451906.8467 - val_mean_squared_error: 1451906.8467
Epoch 249/250
- 0s - loss: 1486580.2059 - mean_squared_error: 1486580.2059 - val_loss: 1449524.4469 - val_mean_squared_error: 1449524.4469
Epoch 250/250
- 0s - loss: 1482848.0573 - mean_squared_error: 1482848.0573 - val_loss: 1445007.3935 - val_mean_squared_error: 1445007.3935
32/13485 [..............................] - ETA: 0s
3968/13485 [=======>......................] - ETA: 0s
6944/13485 [==============>...............] - ETA: 0s
10880/13485 [=======================>......] - ETA: 0s
13485/13485 [==============================] - 0s 14us/step
root mean_squared_error: 1207.313111
After all this hard work we are closer to the MSE we got from linear regression, but purely using a shallow feed-forward neural network.
Training: Gradient Descent
A family of numeric optimization techniques, where we solve a problem with the following pattern:
-
Describe the error in the model output: this is usually some difference between the the true values and the model's predicted values, as a function of the model parameters (weights)
-
Compute the gradient, or directional derivative, of the error -- the "slope toward lower error"
-
Adjust the parameters of the model variables in the indicated direction
-
Repeat

Some ideas to help build your intuition
-
What happens if the variables (imagine just 2, to keep the mental picture simple) are on wildly different scales ... like one ranges from -1 to 1 while another from -1e6 to +1e6?
-
What if some of the variables are correlated? I.e., a change in one corresponds to, say, a linear change in another?
-
Other things being equal, an approximate solution with fewer variables is easier to work with than one with more -- how could we get rid of some less valuable parameters? (e.g., L1 penalty)
-
How do we know how far to "adjust" our parameters with each step?

What if we have billions of data points? Does it makes sense to use all of them for each update? Is there a shortcut?
Yes: Stochastic Gradient Descent
Stochastic gradient descent is an iterative learning algorithm that uses a training dataset to update a model. - The batch size is a hyperparameter of gradient descent that controls the number of training samples to work through before the model's internal parameters are updated. - The number of epochs is a hyperparameter of gradient descent that controls the number of complete passes through the training dataset.
See https://towardsdatascience.com/epoch-vs-iterations-vs-batch-size-4dfb9c7ce9c9.
But SGD has some shortcomings, so we typically use a "smarter" version of SGD, which has rules for adjusting the learning rate and even direction in order to avoid common problems.
What about that "Adam" optimizer? Adam is short for "adaptive moment" and is a variant of SGD that includes momentum calculations that change over time. For more detail on optimizers, see the chapter "Training Deep Neural Nets" in Aurélien Géron's book: Hands-On Machine Learning with Scikit-Learn and TensorFlow (http://shop.oreilly.com/product/0636920052289.do)
See https://keras.io/optimizers/ and references therein.
Training: Backpropagation
With a simple, flat model, we could use SGD or a related algorithm to derive the weights, since the error depends directly on those weights.
With a deeper network, we have a couple of challenges:
- The error is computed from the final layer, so the gradient of the error doesn't tell us immediately about problems in other-layer weights
- Our tiny diamonds model has almost a thousand weights. Bigger models can easily have millions of weights. Each of those weights may need to move a little at a time, and we have to watch out for underflow or undersignificance situations.
The insight is to iteratively calculate errors, one layer at a time, starting at the output. This is called backpropagation. It is neither magical nor surprising. The challenge is just doing it fast and not losing information.

Ok so we've come up with a very slow way to perform a linear regression.
Welcome to Neural Networks in the 1960s!
Watch closely now because this is where the magic happens...

Where does the non-linearity fit in?
- We start with the inputs to a perceptron -- these could be from source data, for example.
- We multiply each input by its respective weight, which gets us the \(x \cdot w\)
- Then add the "bias" -- an extra learnable parameter, to get \({x \cdot w} + b\)
- This value (so far) is sometimes called the "pre-activation"
- Now, apply a non-linear "activation function" to this value, such as the logistic sigmoid

Now the network can "learn" non-linear functions
To gain some intuition, consider that where the sigmoid is close to 1, we can think of that neuron as being "on" or activated, giving a specific output. When close to zero, it is "off."
So each neuron is a bit like a switch. If we have enough of them, we can theoretically express arbitrarily many different signals.
In some ways this is like the original artificial neuron, with the thresholding output -- the main difference is that the sigmoid gives us a smooth (arbitrarily differentiable) output that we can optimize over using gradient descent to learn the weights.
Where does the signal "go" from these neurons?
-
In a regression problem, like the diamonds dataset, the activations from the hidden layer can feed into a single output neuron, with a simple linear activation representing the final output of the calculation.
-
Frequently we want a classification output instead -- e.g., with MNIST digits, where we need to choose from 10 classes. In that case, we can feed the outputs from these hidden neurons forward into a final layer of 10 neurons, and compare those final neurons' activation levels.
Ok, before we talk any more theory, let's run it and see if we can do better on our diamonds dataset adding this "sigmoid activation."
While that's running, let's look at the code:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
import pandas as pd
input_file = "/dbfs/databricks-datasets/Rdatasets/data-001/csv/ggplot2/diamonds.csv"
df = pd.read_csv(input_file, header = 0)
df.drop(df.columns[0], axis=1, inplace=True)
df = pd.get_dummies(df, prefix=['cut_', 'color_', 'clarity_'])
y = df.iloc[:,3:4].values.flatten()
y.flatten()
X = df.drop(df.columns[3], axis=1).values
np.shape(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
model = Sequential()
model.add(Dense(30, input_dim=26, kernel_initializer='normal', activation='sigmoid')) # <- change to nonlinear activation
model.add(Dense(1, kernel_initializer='normal', activation='linear')) # <- activation is linear in output layer for this regression
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mean_squared_error'])
history = model.fit(X_train, y_train, epochs=2000, batch_size=100, validation_split=0.1, verbose=2)
scores = model.evaluate(X_test, y_test)
print("\nroot %s: %f" % (model.metrics_names[1], np.sqrt(scores[1])))
Train on 36409 samples, validate on 4046 samples
Epoch 1/2000
- 1s - loss: 31397235.6558 - mean_squared_error: 31397235.6558 - val_loss: 32383574.7958 - val_mean_squared_error: 32383574.7958
Epoch 2/2000
- 0s - loss: 31327383.7912 - mean_squared_error: 31327383.7912 - val_loss: 32308639.4652 - val_mean_squared_error: 32308639.4652
Epoch 3/2000
- 0s - loss: 31252282.8223 - mean_squared_error: 31252282.8223 - val_loss: 32231016.3836 - val_mean_squared_error: 32231016.3836
Epoch 4/2000
- 0s - loss: 31170289.7380 - mean_squared_error: 31170289.7380 - val_loss: 32144145.4375 - val_mean_squared_error: 32144145.4375
Epoch 5/2000
- 0s - loss: 31083260.5032 - mean_squared_error: 31083260.5032 - val_loss: 32057233.8833 - val_mean_squared_error: 32057233.8833
Epoch 6/2000
- 0s - loss: 31001470.8423 - mean_squared_error: 31001470.8423 - val_loss: 31976492.0554 - val_mean_squared_error: 31976492.0554
Epoch 7/2000
- 0s - loss: 30922894.7525 - mean_squared_error: 30922894.7525 - val_loss: 31897767.1992 - val_mean_squared_error: 31897767.1992
Epoch 8/2000
- 0s - loss: 30845616.8024 - mean_squared_error: 30845616.8024 - val_loss: 31820051.4988 - val_mean_squared_error: 31820051.4988
Epoch 9/2000
- 0s - loss: 30769199.3371 - mean_squared_error: 30769199.3371 - val_loss: 31742996.5240 - val_mean_squared_error: 31742996.5240
Epoch 10/2000
- 0s - loss: 30693446.8908 - mean_squared_error: 30693446.8908 - val_loss: 31666641.7430 - val_mean_squared_error: 31666641.7430
Epoch 11/2000
- 0s - loss: 30618136.4908 - mean_squared_error: 30618136.4908 - val_loss: 31590480.7336 - val_mean_squared_error: 31590480.7336
Epoch 12/2000
- 0s - loss: 30543210.7944 - mean_squared_error: 30543210.7944 - val_loss: 31514667.7736 - val_mean_squared_error: 31514667.7736
Epoch 13/2000
- 0s - loss: 30462755.6179 - mean_squared_error: 30462755.6179 - val_loss: 31430098.2818 - val_mean_squared_error: 31430098.2818
Epoch 14/2000
- 0s - loss: 30382840.9173 - mean_squared_error: 30382840.9173 - val_loss: 31350592.4350 - val_mean_squared_error: 31350592.4350
Epoch 15/2000
- 0s - loss: 30304952.8825 - mean_squared_error: 30304952.8825 - val_loss: 31272120.3500 - val_mean_squared_error: 31272120.3500
Epoch 16/2000
- 0s - loss: 30227645.3064 - mean_squared_error: 30227645.3064 - val_loss: 31194103.1488 - val_mean_squared_error: 31194103.1488
Epoch 17/2000
- 0s - loss: 30150993.0111 - mean_squared_error: 30150993.0111 - val_loss: 31116695.8389 - val_mean_squared_error: 31116695.8389
Epoch 18/2000
- 0s - loss: 30069837.8761 - mean_squared_error: 30069837.8761 - val_loss: 31026249.2397 - val_mean_squared_error: 31026249.2397
Epoch 19/2000
- 0s - loss: 29980447.6209 - mean_squared_error: 29980447.6209 - val_loss: 30939547.4424 - val_mean_squared_error: 30939547.4424
Epoch 20/2000
- 0s - loss: 29896402.2454 - mean_squared_error: 29896402.2454 - val_loss: 30855597.2289 - val_mean_squared_error: 30855597.2289
Epoch 21/2000
- 0s - loss: 29814127.5312 - mean_squared_error: 29814127.5312 - val_loss: 30772653.2219 - val_mean_squared_error: 30772653.2219
Epoch 22/2000
- 0s - loss: 29732678.1205 - mean_squared_error: 29732678.1205 - val_loss: 30690551.4029 - val_mean_squared_error: 30690551.4029
Epoch 23/2000
- 0s - loss: 29651890.3895 - mean_squared_error: 29651890.3895 - val_loss: 30608966.2224 - val_mean_squared_error: 30608966.2224
Epoch 24/2000
- 0s - loss: 29571321.6483 - mean_squared_error: 29571321.6483 - val_loss: 30527517.6352 - val_mean_squared_error: 30527517.6352
Epoch 25/2000
- 0s - loss: 29491328.6854 - mean_squared_error: 29491328.6854 - val_loss: 30446735.6540 - val_mean_squared_error: 30446735.6540
Epoch 26/2000
- 0s - loss: 29411719.3353 - mean_squared_error: 29411719.3353 - val_loss: 30366152.0227 - val_mean_squared_error: 30366152.0227
Epoch 27/2000
- 0s - loss: 29332314.8944 - mean_squared_error: 29332314.8944 - val_loss: 30285836.7108 - val_mean_squared_error: 30285836.7108
Epoch 28/2000
- 0s - loss: 29253317.4112 - mean_squared_error: 29253317.4112 - val_loss: 30205941.9634 - val_mean_squared_error: 30205941.9634
Epoch 29/2000
- 0s - loss: 29174452.6544 - mean_squared_error: 29174452.6544 - val_loss: 30126117.8626 - val_mean_squared_error: 30126117.8626
Epoch 30/2000
- 0s - loss: 29095966.3842 - mean_squared_error: 29095966.3842 - val_loss: 30046719.3356 - val_mean_squared_error: 30046719.3356
Epoch 31/2000
- 0s - loss: 29017649.8682 - mean_squared_error: 29017649.8682 - val_loss: 29967484.1167 - val_mean_squared_error: 29967484.1167
Epoch 32/2000
- 0s - loss: 28939521.5281 - mean_squared_error: 28939521.5281 - val_loss: 29888416.4854 - val_mean_squared_error: 29888416.4854
Epoch 33/2000
- 0s - loss: 28861697.5828 - mean_squared_error: 28861697.5828 - val_loss: 29809702.4281 - val_mean_squared_error: 29809702.4281
Epoch 34/2000
- 0s - loss: 28784209.9575 - mean_squared_error: 28784209.9575 - val_loss: 29731281.6065 - val_mean_squared_error: 29731281.6065
Epoch 35/2000
- 0s - loss: 28706831.1842 - mean_squared_error: 28706831.1842 - val_loss: 29652956.9580 - val_mean_squared_error: 29652956.9580
Epoch 36/2000
- 0s - loss: 28629657.6606 - mean_squared_error: 28629657.6606 - val_loss: 29574874.1651 - val_mean_squared_error: 29574874.1651
Epoch 37/2000
- 0s - loss: 28552852.6089 - mean_squared_error: 28552852.6089 - val_loss: 29497087.4385 - val_mean_squared_error: 29497087.4385
Epoch 38/2000
- 0s - loss: 28476126.3093 - mean_squared_error: 28476126.3093 - val_loss: 29419495.4592 - val_mean_squared_error: 29419495.4592
Epoch 39/2000
- 0s - loss: 28399812.4279 - mean_squared_error: 28399812.4279 - val_loss: 29342199.2081 - val_mean_squared_error: 29342199.2081
Epoch 40/2000
- 0s - loss: 28323720.1345 - mean_squared_error: 28323720.1345 - val_loss: 29265191.3465 - val_mean_squared_error: 29265191.3465
Epoch 41/2000
- 0s - loss: 28247835.7470 - mean_squared_error: 28247835.7470 - val_loss: 29188324.3025 - val_mean_squared_error: 29188324.3025
Epoch 42/2000
- 0s - loss: 28172102.9738 - mean_squared_error: 28172102.9738 - val_loss: 29111682.9619 - val_mean_squared_error: 29111682.9619
Epoch 43/2000
- 0s - loss: 28096726.5860 - mean_squared_error: 28096726.5860 - val_loss: 29035421.8458 - val_mean_squared_error: 29035421.8458
Epoch 44/2000
- 0s - loss: 28021588.4910 - mean_squared_error: 28021588.4910 - val_loss: 28959328.9956 - val_mean_squared_error: 28959328.9956
Epoch 45/2000
- 0s - loss: 27946707.1624 - mean_squared_error: 27946707.1624 - val_loss: 28883512.4706 - val_mean_squared_error: 28883512.4706
Epoch 46/2000
- 0s - loss: 27872025.8892 - mean_squared_error: 27872025.8892 - val_loss: 28807863.5976 - val_mean_squared_error: 28807863.5976
Epoch 47/2000
- 0s - loss: 27797425.4399 - mean_squared_error: 27797425.4399 - val_loss: 28732382.9471 - val_mean_squared_error: 28732382.9471
Epoch 48/2000
- 0s - loss: 27723191.4074 - mean_squared_error: 27723191.4074 - val_loss: 28657206.3253 - val_mean_squared_error: 28657206.3253
Epoch 49/2000
- 0s - loss: 27649192.8975 - mean_squared_error: 27649192.8975 - val_loss: 28582285.1824 - val_mean_squared_error: 28582285.1824
Epoch 50/2000
- 0s - loss: 27575479.0100 - mean_squared_error: 27575479.0100 - val_loss: 28507610.2086 - val_mean_squared_error: 28507610.2086
Epoch 51/2000
- 0s - loss: 27501288.6076 - mean_squared_error: 27501288.6076 - val_loss: 28429080.9985 - val_mean_squared_error: 28429080.9985
Epoch 52/2000
- 0s - loss: 27421728.8021 - mean_squared_error: 27421728.8021 - val_loss: 28349501.5383 - val_mean_squared_error: 28349501.5383
Epoch 53/2000
- 0s - loss: 27344500.0112 - mean_squared_error: 27344500.0112 - val_loss: 28271872.5428 - val_mean_squared_error: 28271872.5428
Epoch 54/2000
- 0s - loss: 27268463.9309 - mean_squared_error: 27268463.9309 - val_loss: 28195175.1132 - val_mean_squared_error: 28195175.1132
Epoch 55/2000
- 0s - loss: 27193075.2804 - mean_squared_error: 27193075.2804 - val_loss: 28118943.3356 - val_mean_squared_error: 28118943.3356
Epoch 56/2000
- 0s - loss: 27118098.0572 - mean_squared_error: 27118098.0572 - val_loss: 28043017.4800 - val_mean_squared_error: 28043017.4800
Epoch 57/2000
- 0s - loss: 27043562.7233 - mean_squared_error: 27043562.7233 - val_loss: 27967574.5348 - val_mean_squared_error: 27967574.5348
Epoch 58/2000
- 0s - loss: 26969328.4123 - mean_squared_error: 26969328.4123 - val_loss: 27892381.2684 - val_mean_squared_error: 27892381.2684
Epoch 59/2000
- 0s - loss: 26895302.7169 - mean_squared_error: 26895302.7169 - val_loss: 27817410.1503 - val_mean_squared_error: 27817410.1503
Epoch 60/2000
- 0s - loss: 26821600.7915 - mean_squared_error: 26821600.7915 - val_loss: 27742831.9179 - val_mean_squared_error: 27742831.9179
Epoch 61/2000
- 0s - loss: 26748231.5481 - mean_squared_error: 26748231.5481 - val_loss: 27668465.3149 - val_mean_squared_error: 27668465.3149
Epoch 62/2000
- 0s - loss: 26674943.8663 - mean_squared_error: 26674943.8663 - val_loss: 27594222.4913 - val_mean_squared_error: 27594222.4913
Epoch 63/2000
- 0s - loss: 26601994.2711 - mean_squared_error: 26601994.2711 - val_loss: 27520427.2951 - val_mean_squared_error: 27520427.2951
Epoch 64/2000
- 0s - loss: 26529282.3881 - mean_squared_error: 26529282.3881 - val_loss: 27446688.2739 - val_mean_squared_error: 27446688.2739
Epoch 65/2000
- 0s - loss: 26457019.9369 - mean_squared_error: 26457019.9369 - val_loss: 27373482.1631 - val_mean_squared_error: 27373482.1631
Epoch 66/2000
- 0s - loss: 26384992.6683 - mean_squared_error: 26384992.6683 - val_loss: 27300497.3604 - val_mean_squared_error: 27300497.3604
Epoch 67/2000
- 0s - loss: 26313104.0731 - mean_squared_error: 26313104.0731 - val_loss: 27227665.3999 - val_mean_squared_error: 27227665.3999
Epoch 68/2000
- 0s - loss: 26241511.5586 - mean_squared_error: 26241511.5586 - val_loss: 27155084.1582 - val_mean_squared_error: 27155084.1582
Epoch 69/2000
- 0s - loss: 26170093.5288 - mean_squared_error: 26170093.5288 - val_loss: 27082711.1349 - val_mean_squared_error: 27082711.1349
Epoch 70/2000
- 0s - loss: 26099043.1046 - mean_squared_error: 26099043.1046 - val_loss: 27010760.2066 - val_mean_squared_error: 27010760.2066
Epoch 71/2000
- 0s - loss: 26028235.2419 - mean_squared_error: 26028235.2419 - val_loss: 26938868.5180 - val_mean_squared_error: 26938868.5180
Epoch 72/2000
- 0s - loss: 25957681.7494 - mean_squared_error: 25957681.7494 - val_loss: 26867434.4795 - val_mean_squared_error: 26867434.4795
Epoch 73/2000
- 0s - loss: 25887375.9710 - mean_squared_error: 25887375.9710 - val_loss: 26796228.9352 - val_mean_squared_error: 26796228.9352
Epoch 74/2000
- 0s - loss: 25817222.8240 - mean_squared_error: 25817222.8240 - val_loss: 26725061.6935 - val_mean_squared_error: 26725061.6935
Epoch 75/2000
- 0s - loss: 25747292.7817 - mean_squared_error: 25747292.7817 - val_loss: 26654194.4212 - val_mean_squared_error: 26654194.4212
Epoch 76/2000
- 0s - loss: 25677706.2037 - mean_squared_error: 25677706.2037 - val_loss: 26583594.1147 - val_mean_squared_error: 26583594.1147
Epoch 77/2000
- 0s - loss: 25608337.1430 - mean_squared_error: 25608337.1430 - val_loss: 26513296.5477 - val_mean_squared_error: 26513296.5477
Epoch 78/2000
- 0s - loss: 25539156.0119 - mean_squared_error: 25539156.0119 - val_loss: 26443137.3040 - val_mean_squared_error: 26443137.3040
Epoch 79/2000
- 0s - loss: 25470427.8616 - mean_squared_error: 25470427.8616 - val_loss: 26373518.7711 - val_mean_squared_error: 26373518.7711
Epoch 80/2000
- 0s - loss: 25401866.0610 - mean_squared_error: 25401866.0610 - val_loss: 26303972.2363 - val_mean_squared_error: 26303972.2363
Epoch 81/2000
- 0s - loss: 25333487.7670 - mean_squared_error: 25333487.7670 - val_loss: 26234631.2130 - val_mean_squared_error: 26234631.2130
Epoch 82/2000
- 0s - loss: 25265550.7323 - mean_squared_error: 25265550.7323 - val_loss: 26165749.3228 - val_mean_squared_error: 26165749.3228
Epoch 83/2000
- 0s - loss: 25197691.5988 - mean_squared_error: 25197691.5988 - val_loss: 26097002.0771 - val_mean_squared_error: 26097002.0771
Epoch 84/2000
- 0s - loss: 25130257.1538 - mean_squared_error: 25130257.1538 - val_loss: 26028667.4909 - val_mean_squared_error: 26028667.4909
Epoch 85/2000
- 0s - loss: 25063019.1388 - mean_squared_error: 25063019.1388 - val_loss: 25960258.2946 - val_mean_squared_error: 25960258.2946
Epoch 86/2000
- 0s - loss: 24995931.5351 - mean_squared_error: 24995931.5351 - val_loss: 25892334.4004 - val_mean_squared_error: 25892334.4004
Epoch 87/2000
- 0s - loss: 24929045.9940 - mean_squared_error: 24929045.9940 - val_loss: 25824543.6985 - val_mean_squared_error: 25824543.6985
Epoch 88/2000
- 0s - loss: 24862549.7085 - mean_squared_error: 24862549.7085 - val_loss: 25757038.2304 - val_mean_squared_error: 25757038.2304
Epoch 89/2000
- 0s - loss: 24796340.2191 - mean_squared_error: 24796340.2191 - val_loss: 25689859.1270 - val_mean_squared_error: 25689859.1270
Epoch 90/2000
- 0s - loss: 24730308.6975 - mean_squared_error: 24730308.6975 - val_loss: 25622882.4706 - val_mean_squared_error: 25622882.4706
Epoch 91/2000
- 0s - loss: 24664616.4917 - mean_squared_error: 24664616.4917 - val_loss: 25556223.6144 - val_mean_squared_error: 25556223.6144
Epoch 92/2000
- 0s - loss: 24599087.1876 - mean_squared_error: 24599087.1876 - val_loss: 25489791.0321 - val_mean_squared_error: 25489791.0321
Epoch 93/2000
- 0s - loss: 24533830.7211 - mean_squared_error: 24533830.7211 - val_loss: 25423553.8339 - val_mean_squared_error: 25423553.8339
Epoch 94/2000
- 0s - loss: 24468854.4123 - mean_squared_error: 24468854.4123 - val_loss: 25357663.3732 - val_mean_squared_error: 25357663.3732
Epoch 95/2000
- 0s - loss: 24404026.7401 - mean_squared_error: 24404026.7401 - val_loss: 25291782.8176 - val_mean_squared_error: 25291782.8176
Epoch 96/2000
- 0s - loss: 24339535.6913 - mean_squared_error: 24339535.6913 - val_loss: 25226405.7410 - val_mean_squared_error: 25226405.7410
Epoch 97/2000
- 0s - loss: 24275298.2234 - mean_squared_error: 24275298.2234 - val_loss: 25161186.7612 - val_mean_squared_error: 25161186.7612
Epoch 98/2000
- 0s - loss: 24211340.8869 - mean_squared_error: 24211340.8869 - val_loss: 25096314.0040 - val_mean_squared_error: 25096314.0040
Epoch 99/2000
- 0s - loss: 24147694.9561 - mean_squared_error: 24147694.9561 - val_loss: 25031670.1819 - val_mean_squared_error: 25031670.1819
Epoch 100/2000
- 0s - loss: 24084192.7054 - mean_squared_error: 24084192.7054 - val_loss: 24967208.1681 - val_mean_squared_error: 24967208.1681
Epoch 101/2000
- 0s - loss: 24020997.9685 - mean_squared_error: 24020997.9685 - val_loss: 24903012.1028 - val_mean_squared_error: 24903012.1028
Epoch 102/2000
- 0s - loss: 23958014.3527 - mean_squared_error: 23958014.3527 - val_loss: 24839094.8265 - val_mean_squared_error: 24839094.8265
Epoch 103/2000
- 0s - loss: 23895302.7699 - mean_squared_error: 23895302.7699 - val_loss: 24775430.5388 - val_mean_squared_error: 24775430.5388
Epoch 104/2000
- 0s - loss: 23832711.7829 - mean_squared_error: 23832711.7829 - val_loss: 24711884.1275 - val_mean_squared_error: 24711884.1275
Epoch 105/2000
- 0s - loss: 23770447.2922 - mean_squared_error: 23770447.2922 - val_loss: 24648619.4217 - val_mean_squared_error: 24648619.4217
Epoch 106/2000
- 0s - loss: 23708384.5371 - mean_squared_error: 23708384.5371 - val_loss: 24585604.6703 - val_mean_squared_error: 24585604.6703
Epoch 107/2000
- 0s - loss: 23646681.5160 - mean_squared_error: 23646681.5160 - val_loss: 24523010.6960 - val_mean_squared_error: 24523010.6960
Epoch 108/2000
- 0s - loss: 23585118.3183 - mean_squared_error: 23585118.3183 - val_loss: 24460488.8799 - val_mean_squared_error: 24460488.8799
Epoch 109/2000
- 0s - loss: 23523883.4182 - mean_squared_error: 23523883.4182 - val_loss: 24398303.1092 - val_mean_squared_error: 24398303.1092
Epoch 110/2000
- 0s - loss: 23462910.2811 - mean_squared_error: 23462910.2811 - val_loss: 24336406.8443 - val_mean_squared_error: 24336406.8443
Epoch 111/2000
- 0s - loss: 23402204.0326 - mean_squared_error: 23402204.0326 - val_loss: 24274770.0376 - val_mean_squared_error: 24274770.0376
Epoch 112/2000
- 0s - loss: 23341832.9642 - mean_squared_error: 23341832.9642 - val_loss: 24213379.6490 - val_mean_squared_error: 24213379.6490
Epoch 113/2000
- 0s - loss: 23279795.8057 - mean_squared_error: 23279795.8057 - val_loss: 24148311.3791 - val_mean_squared_error: 24148311.3791
Epoch 114/2000
- 0s - loss: 23217236.7834 - mean_squared_error: 23217236.7834 - val_loss: 24086002.9946 - val_mean_squared_error: 24086002.9946
Epoch 115/2000
- 0s - loss: 23156625.9503 - mean_squared_error: 23156625.9503 - val_loss: 24024608.4825 - val_mean_squared_error: 24024608.4825
Epoch 116/2000
- 0s - loss: 23096589.0903 - mean_squared_error: 23096589.0903 - val_loss: 23963636.2195 - val_mean_squared_error: 23963636.2195
Epoch 117/2000
- 0s - loss: 23036876.2545 - mean_squared_error: 23036876.2545 - val_loss: 23902991.3623 - val_mean_squared_error: 23902991.3623
Epoch 118/2000
- 0s - loss: 22977437.5939 - mean_squared_error: 22977437.5939 - val_loss: 23842603.3732 - val_mean_squared_error: 23842603.3732
Epoch 119/2000
- 0s - loss: 22918273.3646 - mean_squared_error: 22918273.3646 - val_loss: 23782522.0158 - val_mean_squared_error: 23782522.0158
Epoch 120/2000
- 0s - loss: 22859272.2713 - mean_squared_error: 22859272.2713 - val_loss: 23722539.8853 - val_mean_squared_error: 23722539.8853
Epoch 121/2000
- 0s - loss: 22800737.8453 - mean_squared_error: 22800737.8453 - val_loss: 23663112.8057 - val_mean_squared_error: 23663112.8057
Epoch 122/2000
- 0s - loss: 22742394.6360 - mean_squared_error: 22742394.6360 - val_loss: 23603825.1330 - val_mean_squared_error: 23603825.1330
Epoch 123/2000
- 0s - loss: 22684245.9053 - mean_squared_error: 22684245.9053 - val_loss: 23544635.8824 - val_mean_squared_error: 23544635.8824
Epoch 124/2000
- 0s - loss: 22626413.5138 - mean_squared_error: 22626413.5138 - val_loss: 23485876.2778 - val_mean_squared_error: 23485876.2778
Epoch 125/2000
- 0s - loss: 22568720.6338 - mean_squared_error: 22568720.6338 - val_loss: 23427270.5783 - val_mean_squared_error: 23427270.5783
Epoch 126/2000
- 0s - loss: 22511420.9494 - mean_squared_error: 22511420.9494 - val_loss: 23368986.0880 - val_mean_squared_error: 23368986.0880
Epoch 127/2000
- 0s - loss: 22454394.1190 - mean_squared_error: 22454394.1190 - val_loss: 23311068.8235 - val_mean_squared_error: 23311068.8235
Epoch 128/2000
- 0s - loss: 22397541.9148 - mean_squared_error: 22397541.9148 - val_loss: 23253145.5877 - val_mean_squared_error: 23253145.5877
Epoch 129/2000
- 0s - loss: 22341051.0658 - mean_squared_error: 22341051.0658 - val_loss: 23195790.0475 - val_mean_squared_error: 23195790.0475
Epoch 130/2000
- 0s - loss: 22284655.2844 - mean_squared_error: 22284655.2844 - val_loss: 23138376.5378 - val_mean_squared_error: 23138376.5378
Epoch 131/2000
- 0s - loss: 22228695.7513 - mean_squared_error: 22228695.7513 - val_loss: 23081453.2160 - val_mean_squared_error: 23081453.2160
Epoch 132/2000
- 0s - loss: 22172854.7761 - mean_squared_error: 22172854.7761 - val_loss: 23024590.7385 - val_mean_squared_error: 23024590.7385
Epoch 133/2000
- 0s - loss: 22117285.0639 - mean_squared_error: 22117285.0639 - val_loss: 22968118.0573 - val_mean_squared_error: 22968118.0573
Epoch 134/2000
- 0s - loss: 22061987.1151 - mean_squared_error: 22061987.1151 - val_loss: 22911898.1137 - val_mean_squared_error: 22911898.1137
Epoch 135/2000
- 0s - loss: 22007029.5824 - mean_squared_error: 22007029.5824 - val_loss: 22855873.1587 - val_mean_squared_error: 22855873.1587
Epoch 136/2000
- 0s - loss: 21952235.7935 - mean_squared_error: 21952235.7935 - val_loss: 22800335.4088 - val_mean_squared_error: 22800335.4088
Epoch 137/2000
- 0s - loss: 21897579.2996 - mean_squared_error: 21897579.2996 - val_loss: 22744598.8492 - val_mean_squared_error: 22744598.8492
Epoch 138/2000
- 0s - loss: 21843216.3979 - mean_squared_error: 21843216.3979 - val_loss: 22689297.0005 - val_mean_squared_error: 22689297.0005
Epoch 139/2000
- 0s - loss: 21789164.4874 - mean_squared_error: 21789164.4874 - val_loss: 22634314.9501 - val_mean_squared_error: 22634314.9501
Epoch 140/2000
- 1s - loss: 21735301.7342 - mean_squared_error: 21735301.7342 - val_loss: 22579402.9283 - val_mean_squared_error: 22579402.9283
Epoch 141/2000
- 1s - loss: 21681605.8874 - mean_squared_error: 21681605.8874 - val_loss: 22524827.5185 - val_mean_squared_error: 22524827.5185
Epoch 142/2000
- 0s - loss: 21628268.6495 - mean_squared_error: 21628268.6495 - val_loss: 22470437.9377 - val_mean_squared_error: 22470437.9377
Epoch 143/2000
- 0s - loss: 21575064.8829 - mean_squared_error: 21575064.8829 - val_loss: 22416369.4118 - val_mean_squared_error: 22416369.4118
Epoch 144/2000
- 0s - loss: 21522082.2842 - mean_squared_error: 21522082.2842 - val_loss: 22362375.5818 - val_mean_squared_error: 22362375.5818
Epoch 145/2000
- 0s - loss: 21469363.4439 - mean_squared_error: 21469363.4439 - val_loss: 22308673.4740 - val_mean_squared_error: 22308673.4740
Epoch 146/2000
- 0s - loss: 21416936.7842 - mean_squared_error: 21416936.7842 - val_loss: 22255289.7617 - val_mean_squared_error: 22255289.7617
Epoch 147/2000
- 0s - loss: 21364871.8014 - mean_squared_error: 21364871.8014 - val_loss: 22202402.4785 - val_mean_squared_error: 22202402.4785
Epoch 148/2000
- 0s - loss: 21313050.3111 - mean_squared_error: 21313050.3111 - val_loss: 22149539.6560 - val_mean_squared_error: 22149539.6560
Epoch 149/2000
- 0s - loss: 21261446.3621 - mean_squared_error: 21261446.3621 - val_loss: 22096959.3178 - val_mean_squared_error: 22096959.3178
Epoch 150/2000
- 0s - loss: 21210021.5085 - mean_squared_error: 21210021.5085 - val_loss: 22044621.9871 - val_mean_squared_error: 22044621.9871
Epoch 151/2000
- 0s - loss: 21158849.3865 - mean_squared_error: 21158849.3865 - val_loss: 21992473.2417 - val_mean_squared_error: 21992473.2417
Epoch 152/2000
- 0s - loss: 21107857.0819 - mean_squared_error: 21107857.0819 - val_loss: 21940490.6703 - val_mean_squared_error: 21940490.6703
Epoch 153/2000
- 0s - loss: 21057117.0225 - mean_squared_error: 21057117.0225 - val_loss: 21888891.6738 - val_mean_squared_error: 21888891.6738
Epoch 154/2000
- 0s - loss: 21006774.0317 - mean_squared_error: 21006774.0317 - val_loss: 21837635.9951 - val_mean_squared_error: 21837635.9951
Epoch 155/2000
- 0s - loss: 20956700.9287 - mean_squared_error: 20956700.9287 - val_loss: 21786561.2378 - val_mean_squared_error: 21786561.2378
Epoch 156/2000
- 0s - loss: 20906693.4021 - mean_squared_error: 20906693.4021 - val_loss: 21735692.4320 - val_mean_squared_error: 21735692.4320
Epoch 157/2000
- 0s - loss: 20857150.1686 - mean_squared_error: 20857150.1686 - val_loss: 21685168.9184 - val_mean_squared_error: 21685168.9184
Epoch 158/2000
- 0s - loss: 20807666.7034 - mean_squared_error: 20807666.7034 - val_loss: 21634740.0801 - val_mean_squared_error: 21634740.0801
Epoch 159/2000
- 0s - loss: 20758500.1218 - mean_squared_error: 20758500.1218 - val_loss: 21584612.7355 - val_mean_squared_error: 21584612.7355
Epoch 160/2000
- 0s - loss: 20709524.1605 - mean_squared_error: 20709524.1605 - val_loss: 21534721.3228 - val_mean_squared_error: 21534721.3228
Epoch 161/2000
- 0s - loss: 20660910.6885 - mean_squared_error: 20660910.6885 - val_loss: 21485147.7420 - val_mean_squared_error: 21485147.7420
Epoch 162/2000
- 1s - loss: 20612586.9465 - mean_squared_error: 20612586.9465 - val_loss: 21435754.7781 - val_mean_squared_error: 21435754.7781
Epoch 163/2000
- 0s - loss: 20564474.1311 - mean_squared_error: 20564474.1311 - val_loss: 21386777.7944 - val_mean_squared_error: 21386777.7944
Epoch 164/2000
- 0s - loss: 20516645.5917 - mean_squared_error: 20516645.5917 - val_loss: 21338018.3618 - val_mean_squared_error: 21338018.3618
Epoch 165/2000
- 0s - loss: 20468905.3257 - mean_squared_error: 20468905.3257 - val_loss: 21289250.6525 - val_mean_squared_error: 21289250.6525
Epoch 166/2000
- 0s - loss: 20421415.9548 - mean_squared_error: 20421415.9548 - val_loss: 21240928.0890 - val_mean_squared_error: 21240928.0890
Epoch 167/2000
- 0s - loss: 20374153.5797 - mean_squared_error: 20374153.5797 - val_loss: 21192654.9896 - val_mean_squared_error: 21192654.9896
Epoch 168/2000
- 0s - loss: 20327158.7635 - mean_squared_error: 20327158.7635 - val_loss: 21144689.6471 - val_mean_squared_error: 21144689.6471
Epoch 169/2000
- 1s - loss: 20280455.0811 - mean_squared_error: 20280455.0811 - val_loss: 21097043.4177 - val_mean_squared_error: 21097043.4177
Epoch 170/2000
- 0s - loss: 20233902.1935 - mean_squared_error: 20233902.1935 - val_loss: 21049538.9530 - val_mean_squared_error: 21049538.9530
Epoch 171/2000
- 0s - loss: 20187576.5592 - mean_squared_error: 20187576.5592 - val_loss: 21002178.7395 - val_mean_squared_error: 21002178.7395
Epoch 172/2000
- 0s - loss: 20141522.7279 - mean_squared_error: 20141522.7279 - val_loss: 20955227.2457 - val_mean_squared_error: 20955227.2457
Epoch 173/2000
- 0s - loss: 20095770.7149 - mean_squared_error: 20095770.7149 - val_loss: 20908545.9822 - val_mean_squared_error: 20908545.9822
*** WARNING: skipped 241388 bytes of output ***
Epoch 1833/2000
- 0s - loss: 14086458.4326 - mean_squared_error: 14086458.4326 - val_loss: 14688438.1349 - val_mean_squared_error: 14688438.1349
Epoch 1834/2000
- 0s - loss: 14085434.0234 - mean_squared_error: 14085434.0234 - val_loss: 14687099.8651 - val_mean_squared_error: 14687099.8651
Epoch 1835/2000
- 0s - loss: 14084509.4712 - mean_squared_error: 14084509.4712 - val_loss: 14685995.8003 - val_mean_squared_error: 14685995.8003
Epoch 1836/2000
- 0s - loss: 14083522.1710 - mean_squared_error: 14083522.1710 - val_loss: 14685020.8038 - val_mean_squared_error: 14685020.8038
Epoch 1837/2000
- 0s - loss: 14082602.0144 - mean_squared_error: 14082602.0144 - val_loss: 14684060.2743 - val_mean_squared_error: 14684060.2743
Epoch 1838/2000
- 0s - loss: 14081612.7300 - mean_squared_error: 14081612.7300 - val_loss: 14683103.0138 - val_mean_squared_error: 14683103.0138
Epoch 1839/2000
- 0s - loss: 14080601.5729 - mean_squared_error: 14080601.5729 - val_loss: 14682194.6535 - val_mean_squared_error: 14682194.6535
Epoch 1840/2000
- 0s - loss: 14079617.4989 - mean_squared_error: 14079617.4989 - val_loss: 14681039.8512 - val_mean_squared_error: 14681039.8512
Epoch 1841/2000
- 0s - loss: 14078604.7551 - mean_squared_error: 14078604.7551 - val_loss: 14680020.2279 - val_mean_squared_error: 14680020.2279
Epoch 1842/2000
- 0s - loss: 14077606.6323 - mean_squared_error: 14077606.6323 - val_loss: 14679032.0391 - val_mean_squared_error: 14679032.0391
Epoch 1843/2000
- 0s - loss: 14076695.6481 - mean_squared_error: 14076695.6481 - val_loss: 14678025.0559 - val_mean_squared_error: 14678025.0559
Epoch 1844/2000
- 0s - loss: 14075708.6411 - mean_squared_error: 14075708.6411 - val_loss: 14677170.4572 - val_mean_squared_error: 14677170.4572
Epoch 1845/2000
- 0s - loss: 14074733.2668 - mean_squared_error: 14074733.2668 - val_loss: 14676151.7696 - val_mean_squared_error: 14676151.7696
Epoch 1846/2000
- 0s - loss: 14073722.6215 - mean_squared_error: 14073722.6215 - val_loss: 14675369.2526 - val_mean_squared_error: 14675369.2526
Epoch 1847/2000
- 1s - loss: 14072775.8814 - mean_squared_error: 14072775.8814 - val_loss: 14674029.9896 - val_mean_squared_error: 14674029.9896
Epoch 1848/2000
- 0s - loss: 14071836.2345 - mean_squared_error: 14071836.2345 - val_loss: 14673136.9338 - val_mean_squared_error: 14673136.9338
Epoch 1849/2000
- 0s - loss: 14070810.8924 - mean_squared_error: 14070810.8924 - val_loss: 14672194.3228 - val_mean_squared_error: 14672194.3228
Epoch 1850/2000
- 0s - loss: 14069863.6761 - mean_squared_error: 14069863.6761 - val_loss: 14671299.9367 - val_mean_squared_error: 14671299.9367
Epoch 1851/2000
- 0s - loss: 14068889.2048 - mean_squared_error: 14068889.2048 - val_loss: 14670078.4859 - val_mean_squared_error: 14670078.4859
Epoch 1852/2000
- 0s - loss: 14067938.4834 - mean_squared_error: 14067938.4834 - val_loss: 14669063.5971 - val_mean_squared_error: 14669063.5971
Epoch 1853/2000
- 0s - loss: 14066922.4883 - mean_squared_error: 14066922.4883 - val_loss: 14668091.0554 - val_mean_squared_error: 14668091.0554
Epoch 1854/2000
- 0s - loss: 14065955.6033 - mean_squared_error: 14065955.6033 - val_loss: 14667112.7553 - val_mean_squared_error: 14667112.7553
Epoch 1855/2000
- 0s - loss: 14064991.1939 - mean_squared_error: 14064991.1939 - val_loss: 14666075.4078 - val_mean_squared_error: 14666075.4078
Epoch 1856/2000
- 0s - loss: 14063978.3373 - mean_squared_error: 14063978.3373 - val_loss: 14665110.3134 - val_mean_squared_error: 14665110.3134
Epoch 1857/2000
- 0s - loss: 14063012.4079 - mean_squared_error: 14063012.4079 - val_loss: 14664084.2921 - val_mean_squared_error: 14664084.2921
Epoch 1858/2000
- 0s - loss: 14062046.5409 - mean_squared_error: 14062046.5409 - val_loss: 14663314.2165 - val_mean_squared_error: 14663314.2165
Epoch 1859/2000
- 0s - loss: 14061095.0863 - mean_squared_error: 14061095.0863 - val_loss: 14662105.3094 - val_mean_squared_error: 14662105.3094
Epoch 1860/2000
- 0s - loss: 14060109.7960 - mean_squared_error: 14060109.7960 - val_loss: 14661178.3495 - val_mean_squared_error: 14661178.3495
Epoch 1861/2000
- 0s - loss: 14059102.8300 - mean_squared_error: 14059102.8300 - val_loss: 14660171.9862 - val_mean_squared_error: 14660171.9862
Epoch 1862/2000
- 0s - loss: 14058160.4495 - mean_squared_error: 14058160.4495 - val_loss: 14659101.1468 - val_mean_squared_error: 14659101.1468
Epoch 1863/2000
- 0s - loss: 14057130.4759 - mean_squared_error: 14057130.4759 - val_loss: 14658154.8270 - val_mean_squared_error: 14658154.8270
Epoch 1864/2000
- 0s - loss: 14056215.9189 - mean_squared_error: 14056215.9189 - val_loss: 14657098.5195 - val_mean_squared_error: 14657098.5195
Epoch 1865/2000
- 0s - loss: 14055249.4822 - mean_squared_error: 14055249.4822 - val_loss: 14656309.6268 - val_mean_squared_error: 14656309.6268
Epoch 1866/2000
- 0s - loss: 14054291.7944 - mean_squared_error: 14054291.7944 - val_loss: 14655135.5764 - val_mean_squared_error: 14655135.5764
Epoch 1867/2000
- 0s - loss: 14053316.9188 - mean_squared_error: 14053316.9188 - val_loss: 14654136.7983 - val_mean_squared_error: 14654136.7983
Epoch 1868/2000
- 0s - loss: 14052269.8117 - mean_squared_error: 14052269.8117 - val_loss: 14653555.8601 - val_mean_squared_error: 14653555.8601
Epoch 1869/2000
- 0s - loss: 14051339.1897 - mean_squared_error: 14051339.1897 - val_loss: 14652159.2521 - val_mean_squared_error: 14652159.2521
Epoch 1870/2000
- 0s - loss: 14050346.3569 - mean_squared_error: 14050346.3569 - val_loss: 14651238.4543 - val_mean_squared_error: 14651238.4543
Epoch 1871/2000
- 0s - loss: 14049374.9380 - mean_squared_error: 14049374.9380 - val_loss: 14650198.4182 - val_mean_squared_error: 14650198.4182
Epoch 1872/2000
- 0s - loss: 14048339.0222 - mean_squared_error: 14048339.0222 - val_loss: 14649223.7830 - val_mean_squared_error: 14649223.7830
Epoch 1873/2000
- 0s - loss: 14047460.8214 - mean_squared_error: 14047460.8214 - val_loss: 14648165.3683 - val_mean_squared_error: 14648165.3683
Epoch 1874/2000
- 0s - loss: 14046460.4335 - mean_squared_error: 14046460.4335 - val_loss: 14647232.9313 - val_mean_squared_error: 14647232.9313
Epoch 1875/2000
- 0s - loss: 14045494.6317 - mean_squared_error: 14045494.6317 - val_loss: 14646206.6401 - val_mean_squared_error: 14646206.6401
Epoch 1876/2000
- 0s - loss: 14044518.6021 - mean_squared_error: 14044518.6021 - val_loss: 14645205.3974 - val_mean_squared_error: 14645205.3974
Epoch 1877/2000
- 0s - loss: 14043542.4435 - mean_squared_error: 14043542.4435 - val_loss: 14644302.8868 - val_mean_squared_error: 14644302.8868
Epoch 1878/2000
- 0s - loss: 14042623.7559 - mean_squared_error: 14042623.7559 - val_loss: 14643214.0633 - val_mean_squared_error: 14643214.0633
Epoch 1879/2000
- 0s - loss: 14041576.4189 - mean_squared_error: 14041576.4189 - val_loss: 14642297.2813 - val_mean_squared_error: 14642297.2813
Epoch 1880/2000
- 0s - loss: 14040577.5329 - mean_squared_error: 14040577.5329 - val_loss: 14641284.8616 - val_mean_squared_error: 14641284.8616
Epoch 1881/2000
- 0s - loss: 14039654.2488 - mean_squared_error: 14039654.2488 - val_loss: 14640227.1527 - val_mean_squared_error: 14640227.1527
Epoch 1882/2000
- 0s - loss: 14038650.1586 - mean_squared_error: 14038650.1586 - val_loss: 14639322.6555 - val_mean_squared_error: 14639322.6555
Epoch 1883/2000
- 0s - loss: 14037704.3331 - mean_squared_error: 14037704.3331 - val_loss: 14638298.8942 - val_mean_squared_error: 14638298.8942
Epoch 1884/2000
- 0s - loss: 14036720.1617 - mean_squared_error: 14036720.1617 - val_loss: 14637364.9995 - val_mean_squared_error: 14637364.9995
Epoch 1885/2000
- 0s - loss: 14035740.1378 - mean_squared_error: 14035740.1378 - val_loss: 14636306.6515 - val_mean_squared_error: 14636306.6515
Epoch 1886/2000
- 0s - loss: 14034767.4048 - mean_squared_error: 14034767.4048 - val_loss: 14635277.0662 - val_mean_squared_error: 14635277.0662
Epoch 1887/2000
- 0s - loss: 14033839.9824 - mean_squared_error: 14033839.9824 - val_loss: 14634301.1147 - val_mean_squared_error: 14634301.1147
Epoch 1888/2000
- 0s - loss: 14032845.4022 - mean_squared_error: 14032845.4022 - val_loss: 14633356.0568 - val_mean_squared_error: 14633356.0568
Epoch 1889/2000
- 0s - loss: 14031883.9451 - mean_squared_error: 14031883.9451 - val_loss: 14632473.1379 - val_mean_squared_error: 14632473.1379
Epoch 1890/2000
- 0s - loss: 14030868.8508 - mean_squared_error: 14030868.8508 - val_loss: 14631417.2615 - val_mean_squared_error: 14631417.2615
Epoch 1891/2000
- 0s - loss: 14029889.9388 - mean_squared_error: 14029889.9388 - val_loss: 14630325.6421 - val_mean_squared_error: 14630325.6421
Epoch 1892/2000
- 0s - loss: 14028935.6314 - mean_squared_error: 14028935.6314 - val_loss: 14629574.6817 - val_mean_squared_error: 14629574.6817
Epoch 1893/2000
- 0s - loss: 14027996.0493 - mean_squared_error: 14027996.0493 - val_loss: 14628529.3243 - val_mean_squared_error: 14628529.3243
Epoch 1894/2000
- 0s - loss: 14027005.3169 - mean_squared_error: 14027005.3169 - val_loss: 14627391.1967 - val_mean_squared_error: 14627391.1967
Epoch 1895/2000
- 0s - loss: 14026048.6426 - mean_squared_error: 14026048.6426 - val_loss: 14626388.6139 - val_mean_squared_error: 14626388.6139
Epoch 1896/2000
- 0s - loss: 14025031.5184 - mean_squared_error: 14025031.5184 - val_loss: 14625377.2590 - val_mean_squared_error: 14625377.2590
Epoch 1897/2000
- 0s - loss: 14024054.8359 - mean_squared_error: 14024054.8359 - val_loss: 14624599.2032 - val_mean_squared_error: 14624599.2032
Epoch 1898/2000
- 0s - loss: 14023097.5869 - mean_squared_error: 14023097.5869 - val_loss: 14623391.8893 - val_mean_squared_error: 14623391.8893
Epoch 1899/2000
- 0s - loss: 14022133.5670 - mean_squared_error: 14022133.5670 - val_loss: 14622396.1473 - val_mean_squared_error: 14622396.1473
Epoch 1900/2000
- 0s - loss: 14021144.6183 - mean_squared_error: 14021144.6183 - val_loss: 14621375.9590 - val_mean_squared_error: 14621375.9590
Epoch 1901/2000
- 0s - loss: 14020168.4813 - mean_squared_error: 14020168.4813 - val_loss: 14620391.5175 - val_mean_squared_error: 14620391.5175
Epoch 1902/2000
- 0s - loss: 14019185.7647 - mean_squared_error: 14019185.7647 - val_loss: 14619394.6965 - val_mean_squared_error: 14619394.6965
Epoch 1903/2000
- 0s - loss: 14018240.0450 - mean_squared_error: 14018240.0450 - val_loss: 14618478.2061 - val_mean_squared_error: 14618478.2061
Epoch 1904/2000
- 0s - loss: 14017278.0611 - mean_squared_error: 14017278.0611 - val_loss: 14617430.2546 - val_mean_squared_error: 14617430.2546
Epoch 1905/2000
- 0s - loss: 14016316.0847 - mean_squared_error: 14016316.0847 - val_loss: 14616452.4731 - val_mean_squared_error: 14616452.4731
Epoch 1906/2000
- 0s - loss: 14015343.6848 - mean_squared_error: 14015343.6848 - val_loss: 14615430.9802 - val_mean_squared_error: 14615430.9802
Epoch 1907/2000
- 0s - loss: 14014326.0258 - mean_squared_error: 14014326.0258 - val_loss: 14614445.1933 - val_mean_squared_error: 14614445.1933
Epoch 1908/2000
- 0s - loss: 14013395.7700 - mean_squared_error: 14013395.7700 - val_loss: 14613461.9624 - val_mean_squared_error: 14613461.9624
Epoch 1909/2000
- 0s - loss: 14012363.3592 - mean_squared_error: 14012363.3592 - val_loss: 14612518.7103 - val_mean_squared_error: 14612518.7103
Epoch 1910/2000
- 0s - loss: 14011435.9528 - mean_squared_error: 14011435.9528 - val_loss: 14611503.5304 - val_mean_squared_error: 14611503.5304
Epoch 1911/2000
- 0s - loss: 14010426.8371 - mean_squared_error: 14010426.8371 - val_loss: 14610503.6649 - val_mean_squared_error: 14610503.6649
Epoch 1912/2000
- 0s - loss: 14009488.0206 - mean_squared_error: 14009488.0206 - val_loss: 14609634.6718 - val_mean_squared_error: 14609634.6718
Epoch 1913/2000
- 0s - loss: 14008505.2308 - mean_squared_error: 14008505.2308 - val_loss: 14608588.0242 - val_mean_squared_error: 14608588.0242
Epoch 1914/2000
- 1s - loss: 14007534.5843 - mean_squared_error: 14007534.5843 - val_loss: 14607539.7721 - val_mean_squared_error: 14607539.7721
Epoch 1915/2000
- 1s - loss: 14006574.5376 - mean_squared_error: 14006574.5376 - val_loss: 14606539.5245 - val_mean_squared_error: 14606539.5245
Epoch 1916/2000
- 1s - loss: 14005556.4157 - mean_squared_error: 14005556.4157 - val_loss: 14605521.3895 - val_mean_squared_error: 14605521.3895
Epoch 1917/2000
- 0s - loss: 14004657.1730 - mean_squared_error: 14004657.1730 - val_loss: 14604527.3683 - val_mean_squared_error: 14604527.3683
Epoch 1918/2000
- 0s - loss: 14003640.9749 - mean_squared_error: 14003640.9749 - val_loss: 14603704.9026 - val_mean_squared_error: 14603704.9026
Epoch 1919/2000
- 0s - loss: 14002662.2360 - mean_squared_error: 14002662.2360 - val_loss: 14602829.4483 - val_mean_squared_error: 14602829.4483
Epoch 1920/2000
- 1s - loss: 14001717.1359 - mean_squared_error: 14001717.1359 - val_loss: 14601569.4266 - val_mean_squared_error: 14601569.4266
Epoch 1921/2000
- 1s - loss: 14000717.3413 - mean_squared_error: 14000717.3413 - val_loss: 14600629.5428 - val_mean_squared_error: 14600629.5428
Epoch 1922/2000
- 1s - loss: 13999781.5390 - mean_squared_error: 13999781.5390 - val_loss: 14599680.2531 - val_mean_squared_error: 14599680.2531
Epoch 1923/2000
- 0s - loss: 13998813.2340 - mean_squared_error: 13998813.2340 - val_loss: 14598647.6990 - val_mean_squared_error: 14598647.6990
Epoch 1924/2000
- 0s - loss: 13997831.6735 - mean_squared_error: 13997831.6735 - val_loss: 14597635.7968 - val_mean_squared_error: 14597635.7968
Epoch 1925/2000
- 1s - loss: 13996861.3573 - mean_squared_error: 13996861.3573 - val_loss: 14596606.2121 - val_mean_squared_error: 14596606.2121
Epoch 1926/2000
- 1s - loss: 13995880.4640 - mean_squared_error: 13995880.4640 - val_loss: 14595651.4765 - val_mean_squared_error: 14595651.4765
Epoch 1927/2000
- 0s - loss: 13994892.9043 - mean_squared_error: 13994892.9043 - val_loss: 14594648.9130 - val_mean_squared_error: 14594648.9130
Epoch 1928/2000
- 1s - loss: 13993922.0608 - mean_squared_error: 13993922.0608 - val_loss: 14593825.7469 - val_mean_squared_error: 14593825.7469
Epoch 1929/2000
- 0s - loss: 13992974.8030 - mean_squared_error: 13992974.8030 - val_loss: 14592629.0475 - val_mean_squared_error: 14592629.0475
Epoch 1930/2000
- 1s - loss: 13991971.5907 - mean_squared_error: 13991971.5907 - val_loss: 14591685.5942 - val_mean_squared_error: 14591685.5942
Epoch 1931/2000
- 1s - loss: 13991008.8681 - mean_squared_error: 13991008.8681 - val_loss: 14590691.3915 - val_mean_squared_error: 14590691.3915
Epoch 1932/2000
- 1s - loss: 13990055.1244 - mean_squared_error: 13990055.1244 - val_loss: 14589704.5507 - val_mean_squared_error: 14589704.5507
Epoch 1933/2000
- 1s - loss: 13989088.0260 - mean_squared_error: 13989088.0260 - val_loss: 14588763.9466 - val_mean_squared_error: 14588763.9466
Epoch 1934/2000
- 1s - loss: 13988146.8797 - mean_squared_error: 13988146.8797 - val_loss: 14587764.2353 - val_mean_squared_error: 14587764.2353
Epoch 1935/2000
- 1s - loss: 13987125.8917 - mean_squared_error: 13987125.8917 - val_loss: 14586716.4291 - val_mean_squared_error: 14586716.4291
Epoch 1936/2000
- 1s - loss: 13986166.2039 - mean_squared_error: 13986166.2039 - val_loss: 14585790.5264 - val_mean_squared_error: 14585790.5264
Epoch 1937/2000
- 1s - loss: 13985232.6452 - mean_squared_error: 13985232.6452 - val_loss: 14584743.5902 - val_mean_squared_error: 14584743.5902
Epoch 1938/2000
- 1s - loss: 13984278.0603 - mean_squared_error: 13984278.0603 - val_loss: 14583766.9377 - val_mean_squared_error: 14583766.9377
Epoch 1939/2000
- 1s - loss: 13983262.8058 - mean_squared_error: 13983262.8058 - val_loss: 14583150.8240 - val_mean_squared_error: 14583150.8240
Epoch 1940/2000
- 1s - loss: 13982284.5357 - mean_squared_error: 13982284.5357 - val_loss: 14581842.4533 - val_mean_squared_error: 14581842.4533
Epoch 1941/2000
- 1s - loss: 13981343.8120 - mean_squared_error: 13981343.8120 - val_loss: 14580730.2536 - val_mean_squared_error: 14580730.2536
Epoch 1942/2000
- 1s - loss: 13980322.3916 - mean_squared_error: 13980322.3916 - val_loss: 14579760.0781 - val_mean_squared_error: 14579760.0781
Epoch 1943/2000
- 1s - loss: 13979362.7327 - mean_squared_error: 13979362.7327 - val_loss: 14578797.9862 - val_mean_squared_error: 14578797.9862
Epoch 1944/2000
- 1s - loss: 13978394.7608 - mean_squared_error: 13978394.7608 - val_loss: 14577774.0717 - val_mean_squared_error: 14577774.0717
Epoch 1945/2000
- 1s - loss: 13977455.0814 - mean_squared_error: 13977455.0814 - val_loss: 14576858.7963 - val_mean_squared_error: 14576858.7963
Epoch 1946/2000
- 1s - loss: 13976429.1993 - mean_squared_error: 13976429.1993 - val_loss: 14575857.0514 - val_mean_squared_error: 14575857.0514
Epoch 1947/2000
- 1s - loss: 13975504.5684 - mean_squared_error: 13975504.5684 - val_loss: 14575230.7785 - val_mean_squared_error: 14575230.7785
Epoch 1948/2000
- 1s - loss: 13974535.1979 - mean_squared_error: 13974535.1979 - val_loss: 14573892.8655 - val_mean_squared_error: 14573892.8655
Epoch 1949/2000
- 1s - loss: 13973541.2834 - mean_squared_error: 13973541.2834 - val_loss: 14572876.0929 - val_mean_squared_error: 14572876.0929
Epoch 1950/2000
- 1s - loss: 13972627.5943 - mean_squared_error: 13972627.5943 - val_loss: 14571915.0870 - val_mean_squared_error: 14571915.0870
Epoch 1951/2000
- 1s - loss: 13971644.4700 - mean_squared_error: 13971644.4700 - val_loss: 14570882.7696 - val_mean_squared_error: 14570882.7696
Epoch 1952/2000
- 1s - loss: 13970696.7312 - mean_squared_error: 13970696.7312 - val_loss: 14569891.8141 - val_mean_squared_error: 14569891.8141
Epoch 1953/2000
- 1s - loss: 13969663.0166 - mean_squared_error: 13969663.0166 - val_loss: 14568972.2818 - val_mean_squared_error: 14568972.2818
Epoch 1954/2000
- 1s - loss: 13968782.9991 - mean_squared_error: 13968782.9991 - val_loss: 14567947.0801 - val_mean_squared_error: 14567947.0801
Epoch 1955/2000
- 1s - loss: 13967730.0860 - mean_squared_error: 13967730.0860 - val_loss: 14567092.4567 - val_mean_squared_error: 14567092.4567
Epoch 1956/2000
- 1s - loss: 13966790.8138 - mean_squared_error: 13966790.8138 - val_loss: 14565992.3465 - val_mean_squared_error: 14565992.3465
Epoch 1957/2000
- 1s - loss: 13965827.6534 - mean_squared_error: 13965827.6534 - val_loss: 14564962.4770 - val_mean_squared_error: 14564962.4770
Epoch 1958/2000
- 1s - loss: 13964874.5129 - mean_squared_error: 13964874.5129 - val_loss: 14564002.0074 - val_mean_squared_error: 14564002.0074
Epoch 1959/2000
- 1s - loss: 13963875.4002 - mean_squared_error: 13963875.4002 - val_loss: 14563131.7825 - val_mean_squared_error: 14563131.7825
Epoch 1960/2000
- 1s - loss: 13962938.1506 - mean_squared_error: 13962938.1506 - val_loss: 14562012.5324 - val_mean_squared_error: 14562012.5324
Epoch 1961/2000
- 1s - loss: 13961932.7147 - mean_squared_error: 13961932.7147 - val_loss: 14561060.4523 - val_mean_squared_error: 14561060.4523
Epoch 1962/2000
- 1s - loss: 13960977.4902 - mean_squared_error: 13960977.4902 - val_loss: 14560080.2239 - val_mean_squared_error: 14560080.2239
Epoch 1963/2000
- 1s - loss: 13959991.4240 - mean_squared_error: 13959991.4240 - val_loss: 14559581.7108 - val_mean_squared_error: 14559581.7108
Epoch 1964/2000
- 1s - loss: 13959042.5384 - mean_squared_error: 13959042.5384 - val_loss: 14558281.3435 - val_mean_squared_error: 14558281.3435
Epoch 1965/2000
- 1s - loss: 13958002.1029 - mean_squared_error: 13958002.1029 - val_loss: 14557103.2595 - val_mean_squared_error: 14557103.2595
Epoch 1966/2000
- 1s - loss: 13957110.6674 - mean_squared_error: 13957110.6674 - val_loss: 14556089.4385 - val_mean_squared_error: 14556089.4385
Epoch 1967/2000
- 1s - loss: 13956126.5047 - mean_squared_error: 13956126.5047 - val_loss: 14555112.7884 - val_mean_squared_error: 14555112.7884
Epoch 1968/2000
- 1s - loss: 13955138.1453 - mean_squared_error: 13955138.1453 - val_loss: 14554135.6223 - val_mean_squared_error: 14554135.6223
Epoch 1969/2000
- 1s - loss: 13954155.2029 - mean_squared_error: 13954155.2029 - val_loss: 14553200.1097 - val_mean_squared_error: 14553200.1097
Epoch 1970/2000
- 1s - loss: 13953245.7021 - mean_squared_error: 13953245.7021 - val_loss: 14552137.4904 - val_mean_squared_error: 14552137.4904
Epoch 1971/2000
- 1s - loss: 13952238.0690 - mean_squared_error: 13952238.0690 - val_loss: 14551263.7726 - val_mean_squared_error: 14551263.7726
Epoch 1972/2000
- 1s - loss: 13951232.4036 - mean_squared_error: 13951232.4036 - val_loss: 14550146.3342 - val_mean_squared_error: 14550146.3342
Epoch 1973/2000
- 1s - loss: 13950299.8464 - mean_squared_error: 13950299.8464 - val_loss: 14549223.6060 - val_mean_squared_error: 14549223.6060
Epoch 1974/2000
- 1s - loss: 13949369.3179 - mean_squared_error: 13949369.3179 - val_loss: 14548158.0573 - val_mean_squared_error: 14548158.0573
Epoch 1975/2000
- 1s - loss: 13948345.8805 - mean_squared_error: 13948345.8805 - val_loss: 14547203.9649 - val_mean_squared_error: 14547203.9649
Epoch 1976/2000
- 1s - loss: 13947369.9629 - mean_squared_error: 13947369.9629 - val_loss: 14546559.4800 - val_mean_squared_error: 14546559.4800
Epoch 1977/2000
- 1s - loss: 13946421.5726 - mean_squared_error: 13946421.5726 - val_loss: 14545221.1962 - val_mean_squared_error: 14545221.1962
Epoch 1978/2000
- 1s - loss: 13945421.9250 - mean_squared_error: 13945421.9250 - val_loss: 14544338.6955 - val_mean_squared_error: 14544338.6955
Epoch 1979/2000
- 1s - loss: 13944505.0388 - mean_squared_error: 13944505.0388 - val_loss: 14543509.0623 - val_mean_squared_error: 14543509.0623
Epoch 1980/2000
- 1s - loss: 13943541.5878 - mean_squared_error: 13943541.5878 - val_loss: 14542235.4656 - val_mean_squared_error: 14542235.4656
Epoch 1981/2000
- 1s - loss: 13942526.7038 - mean_squared_error: 13942526.7038 - val_loss: 14541299.3579 - val_mean_squared_error: 14541299.3579
Epoch 1982/2000
- 1s - loss: 13941562.8653 - mean_squared_error: 13941562.8653 - val_loss: 14540301.8443 - val_mean_squared_error: 14540301.8443
Epoch 1983/2000
- 1s - loss: 13940599.2324 - mean_squared_error: 13940599.2324 - val_loss: 14539327.7350 - val_mean_squared_error: 14539327.7350
Epoch 1984/2000
- 1s - loss: 13939643.7045 - mean_squared_error: 13939643.7045 - val_loss: 14538470.0386 - val_mean_squared_error: 14538470.0386
Epoch 1985/2000
- 1s - loss: 13938686.7978 - mean_squared_error: 13938686.7978 - val_loss: 14537338.1977 - val_mean_squared_error: 14537338.1977
Epoch 1986/2000
- 1s - loss: 13937676.0775 - mean_squared_error: 13937676.0775 - val_loss: 14536332.8077 - val_mean_squared_error: 14536332.8077
Epoch 1987/2000
- 1s - loss: 13936761.4252 - mean_squared_error: 13936761.4252 - val_loss: 14535352.2719 - val_mean_squared_error: 14535352.2719
Epoch 1988/2000
- 1s - loss: 13935780.5833 - mean_squared_error: 13935780.5833 - val_loss: 14534363.9086 - val_mean_squared_error: 14534363.9086
Epoch 1989/2000
- 1s - loss: 13934811.6088 - mean_squared_error: 13934811.6088 - val_loss: 14533393.1532 - val_mean_squared_error: 14533393.1532
Epoch 1990/2000
- 1s - loss: 13933816.7718 - mean_squared_error: 13933816.7718 - val_loss: 14532369.0000 - val_mean_squared_error: 14532369.0000
Epoch 1991/2000
- 1s - loss: 13932870.7646 - mean_squared_error: 13932870.7646 - val_loss: 14531386.6288 - val_mean_squared_error: 14531386.6288
Epoch 1992/2000
- 1s - loss: 13931881.5788 - mean_squared_error: 13931881.5788 - val_loss: 14530503.4108 - val_mean_squared_error: 14530503.4108
Epoch 1993/2000
- 1s - loss: 13930933.1328 - mean_squared_error: 13930933.1328 - val_loss: 14529401.6886 - val_mean_squared_error: 14529401.6886
Epoch 1994/2000
- 1s - loss: 13929969.5578 - mean_squared_error: 13929969.5578 - val_loss: 14528616.6149 - val_mean_squared_error: 14528616.6149
Epoch 1995/2000
- 1s - loss: 13929016.3818 - mean_squared_error: 13929016.3818 - val_loss: 14527630.0900 - val_mean_squared_error: 14527630.0900
Epoch 1996/2000
- 1s - loss: 13928019.3752 - mean_squared_error: 13928019.3752 - val_loss: 14526495.1280 - val_mean_squared_error: 14526495.1280
Epoch 1997/2000
- 1s - loss: 13927022.6285 - mean_squared_error: 13927022.6285 - val_loss: 14525727.0074 - val_mean_squared_error: 14525727.0074
Epoch 1998/2000
- 1s - loss: 13926088.6883 - mean_squared_error: 13926088.6883 - val_loss: 14524562.8072 - val_mean_squared_error: 14524562.8072
Epoch 1999/2000
- 1s - loss: 13925121.2566 - mean_squared_error: 13925121.2566 - val_loss: 14523548.8596 - val_mean_squared_error: 14523548.8596
Epoch 2000/2000
- 1s - loss: 13924164.6088 - mean_squared_error: 13924164.6088 - val_loss: 14523216.8319 - val_mean_squared_error: 14523216.8319
32/13485 [..............................] - ETA: 0s
2592/13485 [====>.........................] - ETA: 0s
5088/13485 [==========>...................] - ETA: 0s
8032/13485 [================>.............] - ETA: 0s
10720/13485 [======================>.......] - ETA: 0s
13485/13485 [==============================] - 0s 19us/step
root mean_squared_error: 3707.069044
What is different here?
- We've changed the activation in the hidden layer to "sigmoid" per our discussion.
- Next, notice that we're running 2000 training epochs!
Even so, it takes a looooong time to converge. If you experiment a lot, you'll find that ... it still takes a long time to converge. Around the early part of the most recent deep learning renaissance, researchers started experimenting with other non-linearities.
(Remember, we're talking about non-linear activations in the hidden layer. The output here is still using "linear" rather than "softmax" because we're performing regression, not classification.)
In theory, any non-linearity should allow learning, and maybe we can use one that "works better"
By "works better" we mean
- Simpler gradient - faster to compute
- Less prone to "saturation" -- where the neuron ends up way off in the 0 or 1 territory of the sigmoid and can't easily learn anything
- Keeps gradients "big" -- avoiding the large, flat, near-zero gradient areas of the sigmoid
Turns out that a big breakthrough and popular solution is a very simple hack:
Rectified Linear Unit (ReLU)

Go change your hidden-layer activation from 'sigmoid' to 'relu'
Start your script and watch the error for a bit!
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
import pandas as pd
input_file = "/dbfs/databricks-datasets/Rdatasets/data-001/csv/ggplot2/diamonds.csv"
df = pd.read_csv(input_file, header = 0)
df.drop(df.columns[0], axis=1, inplace=True)
df = pd.get_dummies(df, prefix=['cut_', 'color_', 'clarity_'])
y = df.iloc[:,3:4].values.flatten()
y.flatten()
X = df.drop(df.columns[3], axis=1).values
np.shape(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
model = Sequential()
model.add(Dense(30, input_dim=26, kernel_initializer='normal', activation='relu')) # <--- CHANGE IS HERE
model.add(Dense(1, kernel_initializer='normal', activation='linear'))
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mean_squared_error'])
history = model.fit(X_train, y_train, epochs=2000, batch_size=100, validation_split=0.1, verbose=2)
scores = model.evaluate(X_test, y_test)
print("\nroot %s: %f" % (model.metrics_names[1], np.sqrt(scores[1])))
Train on 36409 samples, validate on 4046 samples
Epoch 1/2000
- 1s - loss: 30189420.8985 - mean_squared_error: 30189420.8985 - val_loss: 28636809.7133 - val_mean_squared_error: 28636809.7133
Epoch 2/2000
- 1s - loss: 23198066.2223 - mean_squared_error: 23198066.2223 - val_loss: 19609172.2017 - val_mean_squared_error: 19609172.2017
Epoch 3/2000
- 1s - loss: 16603911.3175 - mean_squared_error: 16603911.3175 - val_loss: 16048687.6584 - val_mean_squared_error: 16048687.6584
Epoch 4/2000
- 1s - loss: 15165760.0960 - mean_squared_error: 15165760.0960 - val_loss: 15658225.8557 - val_mean_squared_error: 15658225.8557
Epoch 5/2000
- 1s - loss: 14989417.4870 - mean_squared_error: 14989417.4870 - val_loss: 15506647.2674 - val_mean_squared_error: 15506647.2674
Epoch 6/2000
- 1s - loss: 14827583.5424 - mean_squared_error: 14827583.5424 - val_loss: 15322988.9224 - val_mean_squared_error: 15322988.9224
Epoch 7/2000
- 1s - loss: 14640567.4536 - mean_squared_error: 14640567.4536 - val_loss: 15118571.4770 - val_mean_squared_error: 15118571.4770
Epoch 8/2000
- 1s - loss: 14430938.9404 - mean_squared_error: 14430938.9404 - val_loss: 14892813.4118 - val_mean_squared_error: 14892813.4118
Epoch 9/2000
- 1s - loss: 14196182.8864 - mean_squared_error: 14196182.8864 - val_loss: 14636089.3959 - val_mean_squared_error: 14636089.3959
Epoch 10/2000
- 1s - loss: 13933527.4948 - mean_squared_error: 13933527.4948 - val_loss: 14348018.4563 - val_mean_squared_error: 14348018.4563
Epoch 11/2000
- 1s - loss: 13639193.3295 - mean_squared_error: 13639193.3295 - val_loss: 14035286.0519 - val_mean_squared_error: 14035286.0519
Epoch 12/2000
- 1s - loss: 13308997.3142 - mean_squared_error: 13308997.3142 - val_loss: 13662616.8888 - val_mean_squared_error: 13662616.8888
Epoch 13/2000
- 1s - loss: 12935229.2288 - mean_squared_error: 12935229.2288 - val_loss: 13251498.6856 - val_mean_squared_error: 13251498.6856
Epoch 14/2000
- 1s - loss: 12511291.7037 - mean_squared_error: 12511291.7037 - val_loss: 12788027.2852 - val_mean_squared_error: 12788027.2852
Epoch 15/2000
- 1s - loss: 12037879.5633 - mean_squared_error: 12037879.5633 - val_loss: 12273845.5472 - val_mean_squared_error: 12273845.5472
Epoch 16/2000
- 1s - loss: 11514312.3183 - mean_squared_error: 11514312.3183 - val_loss: 11705433.3421 - val_mean_squared_error: 11705433.3421
Epoch 17/2000
- 0s - loss: 10942791.8511 - mean_squared_error: 10942791.8511 - val_loss: 11090956.9812 - val_mean_squared_error: 11090956.9812
Epoch 18/2000
- 0s - loss: 10324517.6534 - mean_squared_error: 10324517.6534 - val_loss: 10432108.8576 - val_mean_squared_error: 10432108.8576
Epoch 19/2000
- 0s - loss: 9672784.8852 - mean_squared_error: 9672784.8852 - val_loss: 9742762.5522 - val_mean_squared_error: 9742762.5522
Epoch 20/2000
- 0s - loss: 8999411.3819 - mean_squared_error: 8999411.3819 - val_loss: 9035512.7736 - val_mean_squared_error: 9035512.7736
Epoch 21/2000
- 0s - loss: 8324484.4254 - mean_squared_error: 8324484.4254 - val_loss: 8336192.3166 - val_mean_squared_error: 8336192.3166
Epoch 22/2000
- 0s - loss: 7667359.0580 - mean_squared_error: 7667359.0580 - val_loss: 7670299.3245 - val_mean_squared_error: 7670299.3245
Epoch 23/2000
- 0s - loss: 7044304.7153 - mean_squared_error: 7044304.7153 - val_loss: 7043340.9703 - val_mean_squared_error: 7043340.9703
Epoch 24/2000
- 0s - loss: 6463977.2148 - mean_squared_error: 6463977.2148 - val_loss: 6448855.0040 - val_mean_squared_error: 6448855.0040
Epoch 25/2000
- 0s - loss: 5929861.5535 - mean_squared_error: 5929861.5535 - val_loss: 5912099.5652 - val_mean_squared_error: 5912099.5652
Epoch 26/2000
- 0s - loss: 5448215.9329 - mean_squared_error: 5448215.9329 - val_loss: 5432970.9488 - val_mean_squared_error: 5432970.9488
Epoch 27/2000
- 0s - loss: 5022827.4511 - mean_squared_error: 5022827.4511 - val_loss: 5010718.1720 - val_mean_squared_error: 5010718.1720
Epoch 28/2000
- 0s - loss: 4649669.4373 - mean_squared_error: 4649669.4373 - val_loss: 4636147.5659 - val_mean_squared_error: 4636147.5659
Epoch 29/2000
- 0s - loss: 4327426.4939 - mean_squared_error: 4327426.4939 - val_loss: 4310399.2614 - val_mean_squared_error: 4310399.2614
Epoch 30/2000
- 0s - loss: 4046344.3449 - mean_squared_error: 4046344.3449 - val_loss: 4023325.6366 - val_mean_squared_error: 4023325.6366
Epoch 31/2000
- 0s - loss: 3797185.8155 - mean_squared_error: 3797185.8155 - val_loss: 3777603.3353 - val_mean_squared_error: 3777603.3353
Epoch 32/2000
- 0s - loss: 3580273.5487 - mean_squared_error: 3580273.5487 - val_loss: 3549745.9894 - val_mean_squared_error: 3549745.9894
Epoch 33/2000
- 0s - loss: 3387090.7587 - mean_squared_error: 3387090.7587 - val_loss: 3343150.4650 - val_mean_squared_error: 3343150.4650
Epoch 34/2000
- 0s - loss: 3214145.2624 - mean_squared_error: 3214145.2624 - val_loss: 3162656.5896 - val_mean_squared_error: 3162656.5896
Epoch 35/2000
- 0s - loss: 3058334.4194 - mean_squared_error: 3058334.4194 - val_loss: 3004862.6919 - val_mean_squared_error: 3004862.6919
Epoch 36/2000
- 0s - loss: 2917225.2674 - mean_squared_error: 2917225.2674 - val_loss: 2846089.5386 - val_mean_squared_error: 2846089.5386
Epoch 37/2000
- 0s - loss: 2785693.9761 - mean_squared_error: 2785693.9761 - val_loss: 2707869.5716 - val_mean_squared_error: 2707869.5716
Epoch 38/2000
- 0s - loss: 2663386.8056 - mean_squared_error: 2663386.8056 - val_loss: 2570811.6094 - val_mean_squared_error: 2570811.6094
Epoch 39/2000
- 0s - loss: 2550473.5284 - mean_squared_error: 2550473.5284 - val_loss: 2448269.9601 - val_mean_squared_error: 2448269.9601
Epoch 40/2000
- 0s - loss: 2447714.5338 - mean_squared_error: 2447714.5338 - val_loss: 2339941.2572 - val_mean_squared_error: 2339941.2572
Epoch 41/2000
- 0s - loss: 2354000.8045 - mean_squared_error: 2354000.8045 - val_loss: 2230314.2221 - val_mean_squared_error: 2230314.2221
Epoch 42/2000
- 0s - loss: 2265501.9560 - mean_squared_error: 2265501.9560 - val_loss: 2135751.3114 - val_mean_squared_error: 2135751.3114
Epoch 43/2000
- 0s - loss: 2184753.3058 - mean_squared_error: 2184753.3058 - val_loss: 2047332.1391 - val_mean_squared_error: 2047332.1391
Epoch 44/2000
- 0s - loss: 2112292.5049 - mean_squared_error: 2112292.5049 - val_loss: 1965993.4016 - val_mean_squared_error: 1965993.4016
Epoch 45/2000
- 0s - loss: 2044595.5458 - mean_squared_error: 2044595.5458 - val_loss: 1891222.9977 - val_mean_squared_error: 1891222.9977
Epoch 46/2000
- 0s - loss: 1981209.5128 - mean_squared_error: 1981209.5128 - val_loss: 1822348.1388 - val_mean_squared_error: 1822348.1388
Epoch 47/2000
- 0s - loss: 1924395.7817 - mean_squared_error: 1924395.7817 - val_loss: 1764530.3743 - val_mean_squared_error: 1764530.3743
Epoch 48/2000
- 0s - loss: 1869240.8064 - mean_squared_error: 1869240.8064 - val_loss: 1699779.9201 - val_mean_squared_error: 1699779.9201
Epoch 49/2000
- 0s - loss: 1818964.0647 - mean_squared_error: 1818964.0647 - val_loss: 1642916.4305 - val_mean_squared_error: 1642916.4305
Epoch 50/2000
- 0s - loss: 1772949.7733 - mean_squared_error: 1772949.7733 - val_loss: 1589150.5234 - val_mean_squared_error: 1589150.5234
Epoch 51/2000
- 0s - loss: 1728289.2533 - mean_squared_error: 1728289.2533 - val_loss: 1540550.6556 - val_mean_squared_error: 1540550.6556
Epoch 52/2000
- 0s - loss: 1686578.8149 - mean_squared_error: 1686578.8149 - val_loss: 1493753.4956 - val_mean_squared_error: 1493753.4956
Epoch 53/2000
- 0s - loss: 1648652.4508 - mean_squared_error: 1648652.4508 - val_loss: 1458841.1140 - val_mean_squared_error: 1458841.1140
Epoch 54/2000
- 0s - loss: 1611433.7462 - mean_squared_error: 1611433.7462 - val_loss: 1409693.2003 - val_mean_squared_error: 1409693.2003
Epoch 55/2000
- 0s - loss: 1576917.2249 - mean_squared_error: 1576917.2249 - val_loss: 1372174.2692 - val_mean_squared_error: 1372174.2692
Epoch 56/2000
- 0s - loss: 1544672.2450 - mean_squared_error: 1544672.2450 - val_loss: 1336006.0685 - val_mean_squared_error: 1336006.0685
Epoch 57/2000
- 0s - loss: 1515766.5707 - mean_squared_error: 1515766.5707 - val_loss: 1304437.5853 - val_mean_squared_error: 1304437.5853
Epoch 58/2000
- 0s - loss: 1487106.1103 - mean_squared_error: 1487106.1103 - val_loss: 1271618.0805 - val_mean_squared_error: 1271618.0805
Epoch 59/2000
- 0s - loss: 1457997.5480 - mean_squared_error: 1457997.5480 - val_loss: 1242240.4967 - val_mean_squared_error: 1242240.4967
Epoch 60/2000
- 0s - loss: 1433937.3561 - mean_squared_error: 1433937.3561 - val_loss: 1213240.8568 - val_mean_squared_error: 1213240.8568
Epoch 61/2000
- 0s - loss: 1409274.3087 - mean_squared_error: 1409274.3087 - val_loss: 1191901.4261 - val_mean_squared_error: 1191901.4261
Epoch 62/2000
- 0s - loss: 1387124.1232 - mean_squared_error: 1387124.1232 - val_loss: 1166198.4036 - val_mean_squared_error: 1166198.4036
Epoch 63/2000
- 0s - loss: 1367341.6098 - mean_squared_error: 1367341.6098 - val_loss: 1144052.0850 - val_mean_squared_error: 1144052.0850
Epoch 64/2000
- 0s - loss: 1348362.6727 - mean_squared_error: 1348362.6727 - val_loss: 1122819.6877 - val_mean_squared_error: 1122819.6877
Epoch 65/2000
- 0s - loss: 1329934.3085 - mean_squared_error: 1329934.3085 - val_loss: 1101036.6601 - val_mean_squared_error: 1101036.6601
Epoch 66/2000
- 0s - loss: 1313865.1430 - mean_squared_error: 1313865.1430 - val_loss: 1087398.2983 - val_mean_squared_error: 1087398.2983
Epoch 67/2000
- 0s - loss: 1297733.6369 - mean_squared_error: 1297733.6369 - val_loss: 1068921.9223 - val_mean_squared_error: 1068921.9223
Epoch 68/2000
- 0s - loss: 1283105.7054 - mean_squared_error: 1283105.7054 - val_loss: 1052849.1446 - val_mean_squared_error: 1052849.1446
Epoch 69/2000
- 0s - loss: 1269226.2389 - mean_squared_error: 1269226.2389 - val_loss: 1038531.1632 - val_mean_squared_error: 1038531.1632
Epoch 70/2000
- 0s - loss: 1254929.9186 - mean_squared_error: 1254929.9186 - val_loss: 1023195.2031 - val_mean_squared_error: 1023195.2031
Epoch 71/2000
- 0s - loss: 1242275.6744 - mean_squared_error: 1242275.6744 - val_loss: 1004922.5253 - val_mean_squared_error: 1004922.5253
Epoch 72/2000
- 0s - loss: 1231293.5488 - mean_squared_error: 1231293.5488 - val_loss: 991712.2193 - val_mean_squared_error: 991712.2193
Epoch 73/2000
- 0s - loss: 1219624.4148 - mean_squared_error: 1219624.4148 - val_loss: 979516.0057 - val_mean_squared_error: 979516.0057
Epoch 74/2000
- 0s - loss: 1208870.5152 - mean_squared_error: 1208870.5152 - val_loss: 968570.3547 - val_mean_squared_error: 968570.3547
Epoch 75/2000
- 0s - loss: 1198596.5433 - mean_squared_error: 1198596.5433 - val_loss: 957311.5155 - val_mean_squared_error: 957311.5155
Epoch 76/2000
- 0s - loss: 1188799.8814 - mean_squared_error: 1188799.8814 - val_loss: 945335.0963 - val_mean_squared_error: 945335.0963
Epoch 77/2000
- 0s - loss: 1179789.8610 - mean_squared_error: 1179789.8610 - val_loss: 940609.4587 - val_mean_squared_error: 940609.4587
Epoch 78/2000
- 0s - loss: 1170511.9571 - mean_squared_error: 1170511.9571 - val_loss: 925838.4326 - val_mean_squared_error: 925838.4326
Epoch 79/2000
- 0s - loss: 1162717.7094 - mean_squared_error: 1162717.7094 - val_loss: 918393.0366 - val_mean_squared_error: 918393.0366
Epoch 80/2000
- 0s - loss: 1155802.0771 - mean_squared_error: 1155802.0771 - val_loss: 909008.6373 - val_mean_squared_error: 909008.6373
Epoch 81/2000
- 0s - loss: 1147283.3683 - mean_squared_error: 1147283.3683 - val_loss: 899639.5847 - val_mean_squared_error: 899639.5847
Epoch 82/2000
- 0s - loss: 1139978.5240 - mean_squared_error: 1139978.5240 - val_loss: 893100.5091 - val_mean_squared_error: 893100.5091
Epoch 83/2000
- 0s - loss: 1133857.4649 - mean_squared_error: 1133857.4649 - val_loss: 886380.4719 - val_mean_squared_error: 886380.4719
Epoch 84/2000
- 0s - loss: 1126496.1330 - mean_squared_error: 1126496.1330 - val_loss: 883940.9976 - val_mean_squared_error: 883940.9976
Epoch 85/2000
- 0s - loss: 1119351.9238 - mean_squared_error: 1119351.9238 - val_loss: 873083.9504 - val_mean_squared_error: 873083.9504
Epoch 86/2000
- 0s - loss: 1113990.1621 - mean_squared_error: 1113990.1621 - val_loss: 865655.3887 - val_mean_squared_error: 865655.3887
Epoch 87/2000
- 0s - loss: 1107928.8959 - mean_squared_error: 1107928.8959 - val_loss: 873964.5185 - val_mean_squared_error: 873964.5185
Epoch 88/2000
- 0s - loss: 1101927.3729 - mean_squared_error: 1101927.3729 - val_loss: 861648.0959 - val_mean_squared_error: 861648.0959
Epoch 89/2000
- 0s - loss: 1096059.7178 - mean_squared_error: 1096059.7178 - val_loss: 845345.2097 - val_mean_squared_error: 845345.2097
Epoch 90/2000
- 0s - loss: 1090183.0421 - mean_squared_error: 1090183.0421 - val_loss: 838976.3949 - val_mean_squared_error: 838976.3949
Epoch 91/2000
- 0s - loss: 1085125.6741 - mean_squared_error: 1085125.6741 - val_loss: 834308.7424 - val_mean_squared_error: 834308.7424
Epoch 92/2000
- 0s - loss: 1079960.3373 - mean_squared_error: 1079960.3373 - val_loss: 827018.7170 - val_mean_squared_error: 827018.7170
Epoch 93/2000
- 0s - loss: 1075016.3585 - mean_squared_error: 1075016.3585 - val_loss: 824307.1723 - val_mean_squared_error: 824307.1723
Epoch 94/2000
- 0s - loss: 1069779.9771 - mean_squared_error: 1069779.9771 - val_loss: 815420.9564 - val_mean_squared_error: 815420.9564
Epoch 95/2000
- 0s - loss: 1065536.1922 - mean_squared_error: 1065536.1922 - val_loss: 815212.7480 - val_mean_squared_error: 815212.7480
Epoch 96/2000
- 0s - loss: 1060357.2113 - mean_squared_error: 1060357.2113 - val_loss: 806200.7524 - val_mean_squared_error: 806200.7524
Epoch 97/2000
- 0s - loss: 1055606.6725 - mean_squared_error: 1055606.6725 - val_loss: 815764.0978 - val_mean_squared_error: 815764.0978
Epoch 98/2000
- 0s - loss: 1052198.3024 - mean_squared_error: 1052198.3024 - val_loss: 796517.7568 - val_mean_squared_error: 796517.7568
Epoch 99/2000
- 0s - loss: 1047813.9664 - mean_squared_error: 1047813.9664 - val_loss: 792303.8808 - val_mean_squared_error: 792303.8808
Epoch 100/2000
- 0s - loss: 1043633.2012 - mean_squared_error: 1043633.2012 - val_loss: 792735.2539 - val_mean_squared_error: 792735.2539
Epoch 101/2000
- 0s - loss: 1039242.1259 - mean_squared_error: 1039242.1259 - val_loss: 785669.7569 - val_mean_squared_error: 785669.7569
Epoch 102/2000
- 0s - loss: 1035018.1389 - mean_squared_error: 1035018.1389 - val_loss: 779840.4313 - val_mean_squared_error: 779840.4313
Epoch 103/2000
- 0s - loss: 1030598.0931 - mean_squared_error: 1030598.0931 - val_loss: 781102.4054 - val_mean_squared_error: 781102.4054
Epoch 104/2000
- 0s - loss: 1026942.8171 - mean_squared_error: 1026942.8171 - val_loss: 774531.1024 - val_mean_squared_error: 774531.1024
Epoch 105/2000
- 0s - loss: 1023330.2583 - mean_squared_error: 1023330.2583 - val_loss: 767568.0108 - val_mean_squared_error: 767568.0108
Epoch 106/2000
- 0s - loss: 1019163.5211 - mean_squared_error: 1019163.5211 - val_loss: 773755.5281 - val_mean_squared_error: 773755.5281
Epoch 107/2000
- 0s - loss: 1015504.6994 - mean_squared_error: 1015504.6994 - val_loss: 761746.3565 - val_mean_squared_error: 761746.3565
Epoch 108/2000
- 0s - loss: 1012240.3183 - mean_squared_error: 1012240.3183 - val_loss: 758921.7005 - val_mean_squared_error: 758921.7005
Epoch 109/2000
- 0s - loss: 1008086.6043 - mean_squared_error: 1008086.6043 - val_loss: 752427.9384 - val_mean_squared_error: 752427.9384
Epoch 110/2000
- 0s - loss: 1004775.1231 - mean_squared_error: 1004775.1231 - val_loss: 748668.6899 - val_mean_squared_error: 748668.6899
Epoch 111/2000
- 0s - loss: 1001015.0934 - mean_squared_error: 1001015.0934 - val_loss: 745433.2375 - val_mean_squared_error: 745433.2375
Epoch 112/2000
- 0s - loss: 997149.6093 - mean_squared_error: 997149.6093 - val_loss: 746147.8102 - val_mean_squared_error: 746147.8102
Epoch 113/2000
- 0s - loss: 994264.0145 - mean_squared_error: 994264.0145 - val_loss: 740447.2325 - val_mean_squared_error: 740447.2325
Epoch 114/2000
- 0s - loss: 990874.0751 - mean_squared_error: 990874.0751 - val_loss: 752904.6843 - val_mean_squared_error: 752904.6843
Epoch 115/2000
- 0s - loss: 988689.3808 - mean_squared_error: 988689.3808 - val_loss: 738193.1483 - val_mean_squared_error: 738193.1483
Epoch 116/2000
- 0s - loss: 984721.8802 - mean_squared_error: 984721.8802 - val_loss: 728698.0477 - val_mean_squared_error: 728698.0477
Epoch 117/2000
- 0s - loss: 981724.4628 - mean_squared_error: 981724.4628 - val_loss: 726934.4692 - val_mean_squared_error: 726934.4692
Epoch 118/2000
- 0s - loss: 978402.5133 - mean_squared_error: 978402.5133 - val_loss: 724588.1015 - val_mean_squared_error: 724588.1015
Epoch 119/2000
- 0s - loss: 974883.3142 - mean_squared_error: 974883.3142 - val_loss: 719651.9469 - val_mean_squared_error: 719651.9469
Epoch 120/2000
- 0s - loss: 972348.5150 - mean_squared_error: 972348.5150 - val_loss: 723171.7312 - val_mean_squared_error: 723171.7312
Epoch 121/2000
- 0s - loss: 969273.4995 - mean_squared_error: 969273.4995 - val_loss: 715898.5582 - val_mean_squared_error: 715898.5582
Epoch 122/2000
- 0s - loss: 966046.4831 - mean_squared_error: 966046.4831 - val_loss: 721566.7988 - val_mean_squared_error: 721566.7988
Epoch 123/2000
- 0s - loss: 963870.3004 - mean_squared_error: 963870.3004 - val_loss: 713585.8379 - val_mean_squared_error: 713585.8379
Epoch 124/2000
- 0s - loss: 960399.8889 - mean_squared_error: 960399.8889 - val_loss: 706410.6038 - val_mean_squared_error: 706410.6038
Epoch 125/2000
- 0s - loss: 958589.1116 - mean_squared_error: 958589.1116 - val_loss: 705770.9541 - val_mean_squared_error: 705770.9541
Epoch 126/2000
- 0s - loss: 955909.8628 - mean_squared_error: 955909.8628 - val_loss: 707573.5642 - val_mean_squared_error: 707573.5642
Epoch 127/2000
- 0s - loss: 953370.5705 - mean_squared_error: 953370.5705 - val_loss: 703662.7318 - val_mean_squared_error: 703662.7318
Epoch 128/2000
- 0s - loss: 950355.3206 - mean_squared_error: 950355.3206 - val_loss: 705298.0371 - val_mean_squared_error: 705298.0371
Epoch 129/2000
- 0s - loss: 947470.5564 - mean_squared_error: 947470.5564 - val_loss: 694944.4235 - val_mean_squared_error: 694944.4235
Epoch 130/2000
- 0s - loss: 945568.4066 - mean_squared_error: 945568.4066 - val_loss: 692030.7021 - val_mean_squared_error: 692030.7021
Epoch 131/2000
- 0s - loss: 943050.2850 - mean_squared_error: 943050.2850 - val_loss: 699362.5001 - val_mean_squared_error: 699362.5001
Epoch 132/2000
- 0s - loss: 939632.1378 - mean_squared_error: 939632.1378 - val_loss: 691716.7484 - val_mean_squared_error: 691716.7484
Epoch 133/2000
- 0s - loss: 937285.4758 - mean_squared_error: 937285.4758 - val_loss: 690304.0487 - val_mean_squared_error: 690304.0487
Epoch 134/2000
- 0s - loss: 935539.2472 - mean_squared_error: 935539.2472 - val_loss: 684200.6772 - val_mean_squared_error: 684200.6772
Epoch 135/2000
- 0s - loss: 932167.0026 - mean_squared_error: 932167.0026 - val_loss: 681388.0945 - val_mean_squared_error: 681388.0945
Epoch 136/2000
- 0s - loss: 929939.8893 - mean_squared_error: 929939.8893 - val_loss: 682788.7851 - val_mean_squared_error: 682788.7851
Epoch 137/2000
- 0s - loss: 927668.1191 - mean_squared_error: 927668.1191 - val_loss: 679113.7417 - val_mean_squared_error: 679113.7417
Epoch 138/2000
- 0s - loss: 926008.5818 - mean_squared_error: 926008.5818 - val_loss: 676147.3046 - val_mean_squared_error: 676147.3046
Epoch 139/2000
- 0s - loss: 923048.2713 - mean_squared_error: 923048.2713 - val_loss: 677156.4186 - val_mean_squared_error: 677156.4186
Epoch 140/2000
- 0s - loss: 920688.1663 - mean_squared_error: 920688.1663 - val_loss: 672482.7448 - val_mean_squared_error: 672482.7448
Epoch 141/2000
- 0s - loss: 919837.8943 - mean_squared_error: 919837.8943 - val_loss: 670414.9576 - val_mean_squared_error: 670414.9576
Epoch 142/2000
- 0s - loss: 916313.0555 - mean_squared_error: 916313.0555 - val_loss: 685471.9791 - val_mean_squared_error: 685471.9791
Epoch 143/2000
- 0s - loss: 915272.9670 - mean_squared_error: 915272.9670 - val_loss: 668524.5762 - val_mean_squared_error: 668524.5762
Epoch 144/2000
- 0s - loss: 912336.0104 - mean_squared_error: 912336.0104 - val_loss: 674249.9691 - val_mean_squared_error: 674249.9691
Epoch 145/2000
- 0s - loss: 910291.7740 - mean_squared_error: 910291.7740 - val_loss: 663560.6815 - val_mean_squared_error: 663560.6815
Epoch 146/2000
- 0s - loss: 908166.9091 - mean_squared_error: 908166.9091 - val_loss: 661399.2248 - val_mean_squared_error: 661399.2248
Epoch 147/2000
- 0s - loss: 905912.1078 - mean_squared_error: 905912.1078 - val_loss: 667400.1303 - val_mean_squared_error: 667400.1303
Epoch 148/2000
- 0s - loss: 903832.7466 - mean_squared_error: 903832.7466 - val_loss: 664925.2466 - val_mean_squared_error: 664925.2466
Epoch 149/2000
- 0s - loss: 901111.1322 - mean_squared_error: 901111.1322 - val_loss: 656424.3131 - val_mean_squared_error: 656424.3131
Epoch 150/2000
- 0s - loss: 899936.9588 - mean_squared_error: 899936.9588 - val_loss: 655574.3051 - val_mean_squared_error: 655574.3051
Epoch 151/2000
- 0s - loss: 897709.8877 - mean_squared_error: 897709.8877 - val_loss: 653072.2465 - val_mean_squared_error: 653072.2465
Epoch 152/2000
- 0s - loss: 895961.3970 - mean_squared_error: 895961.3970 - val_loss: 653385.8794 - val_mean_squared_error: 653385.8794
Epoch 153/2000
- 0s - loss: 894145.2104 - mean_squared_error: 894145.2104 - val_loss: 650049.8083 - val_mean_squared_error: 650049.8083
Epoch 154/2000
- 0s - loss: 892313.8828 - mean_squared_error: 892313.8828 - val_loss: 651325.9268 - val_mean_squared_error: 651325.9268
Epoch 155/2000
- 0s - loss: 890755.4445 - mean_squared_error: 890755.4445 - val_loss: 651107.3247 - val_mean_squared_error: 651107.3247
Epoch 156/2000
- 0s - loss: 888268.6103 - mean_squared_error: 888268.6103 - val_loss: 649560.8445 - val_mean_squared_error: 649560.8445
Epoch 157/2000
- 0s - loss: 887101.2549 - mean_squared_error: 887101.2549 - val_loss: 649862.3474 - val_mean_squared_error: 649862.3474
Epoch 158/2000
- 0s - loss: 884886.7809 - mean_squared_error: 884886.7809 - val_loss: 642837.5409 - val_mean_squared_error: 642837.5409
Epoch 159/2000
- 0s - loss: 883092.6271 - mean_squared_error: 883092.6271 - val_loss: 645735.0666 - val_mean_squared_error: 645735.0666
Epoch 160/2000
- 0s - loss: 881120.0721 - mean_squared_error: 881120.0721 - val_loss: 642229.4987 - val_mean_squared_error: 642229.4987
Epoch 161/2000
- 0s - loss: 879317.6468 - mean_squared_error: 879317.6468 - val_loss: 649237.6002 - val_mean_squared_error: 649237.6002
Epoch 162/2000
- 0s - loss: 877933.4986 - mean_squared_error: 877933.4986 - val_loss: 645492.1847 - val_mean_squared_error: 645492.1847
Epoch 163/2000
- 0s - loss: 876311.9927 - mean_squared_error: 876311.9927 - val_loss: 638299.4104 - val_mean_squared_error: 638299.4104
Epoch 164/2000
- 0s - loss: 874368.5659 - mean_squared_error: 874368.5659 - val_loss: 639309.5914 - val_mean_squared_error: 639309.5914
Epoch 165/2000
- 0s - loss: 871988.8340 - mean_squared_error: 871988.8340 - val_loss: 636048.8807 - val_mean_squared_error: 636048.8807
Epoch 166/2000
- 0s - loss: 871099.2410 - mean_squared_error: 871099.2410 - val_loss: 633811.7354 - val_mean_squared_error: 633811.7354
Epoch 167/2000
- 0s - loss: 869259.6353 - mean_squared_error: 869259.6353 - val_loss: 631700.6498 - val_mean_squared_error: 631700.6498
Epoch 168/2000
- 0s - loss: 867846.2387 - mean_squared_error: 867846.2387 - val_loss: 631306.9374 - val_mean_squared_error: 631306.9374
Epoch 169/2000
- 0s - loss: 867124.9870 - mean_squared_error: 867124.9870 - val_loss: 630908.5872 - val_mean_squared_error: 630908.5872
Epoch 170/2000
- 0s - loss: 865043.7359 - mean_squared_error: 865043.7359 - val_loss: 628584.2976 - val_mean_squared_error: 628584.2976
Epoch 171/2000
- 0s - loss: 862503.4103 - mean_squared_error: 862503.4103 - val_loss: 636332.0420 - val_mean_squared_error: 636332.0420
Epoch 172/2000
- 0s - loss: 861153.7802 - mean_squared_error: 861153.7802 - val_loss: 627266.2563 - val_mean_squared_error: 627266.2563
Epoch 173/2000
- 0s - loss: 859494.3078 - mean_squared_error: 859494.3078 - val_loss: 624305.4543 - val_mean_squared_error: 624305.4543
Epoch 174/2000
- 0s - loss: 858547.6955 - mean_squared_error: 858547.6955 - val_loss: 630155.4827 - val_mean_squared_error: 630155.4827
Epoch 175/2000
- 0s - loss: 856202.1055 - mean_squared_error: 856202.1055 - val_loss: 623894.7843 - val_mean_squared_error: 623894.7843
Epoch 176/2000
- 0s - loss: 854444.2765 - mean_squared_error: 854444.2765 - val_loss: 623929.4103 - val_mean_squared_error: 623929.4103
Epoch 177/2000
- 0s - loss: 853613.5416 - mean_squared_error: 853613.5416 - val_loss: 622482.8054 - val_mean_squared_error: 622482.8054
Epoch 178/2000
- 0s - loss: 852153.3314 - mean_squared_error: 852153.3314 - val_loss: 621689.6013 - val_mean_squared_error: 621689.6013
Epoch 179/2000
- 0s - loss: 849991.4039 - mean_squared_error: 849991.4039 - val_loss: 618582.9728 - val_mean_squared_error: 618582.9728
Epoch 180/2000
- 0s - loss: 848670.8722 - mean_squared_error: 848670.8722 - val_loss: 617514.6323 - val_mean_squared_error: 617514.6323
*** WARNING: skipped 225777 bytes of output ***
Epoch 1823/2000
- 0s - loss: 352445.9751 - mean_squared_error: 352445.9751 - val_loss: 322069.3224 - val_mean_squared_error: 322069.3224
Epoch 1824/2000
- 0s - loss: 352472.1113 - mean_squared_error: 352472.1113 - val_loss: 322258.6551 - val_mean_squared_error: 322258.6551
Epoch 1825/2000
- 0s - loss: 352828.0406 - mean_squared_error: 352828.0406 - val_loss: 322122.4397 - val_mean_squared_error: 322122.4397
Epoch 1826/2000
- 0s - loss: 352703.0477 - mean_squared_error: 352703.0477 - val_loss: 323740.2058 - val_mean_squared_error: 323740.2058
Epoch 1827/2000
- 0s - loss: 352640.1232 - mean_squared_error: 352640.1232 - val_loss: 321345.6100 - val_mean_squared_error: 321345.6100
Epoch 1828/2000
- 0s - loss: 352718.0216 - mean_squared_error: 352718.0216 - val_loss: 322241.4297 - val_mean_squared_error: 322241.4297
Epoch 1829/2000
- 0s - loss: 353036.8003 - mean_squared_error: 353036.8003 - val_loss: 321266.4523 - val_mean_squared_error: 321266.4523
Epoch 1830/2000
- 0s - loss: 352526.1196 - mean_squared_error: 352526.1196 - val_loss: 322149.5655 - val_mean_squared_error: 322149.5655
Epoch 1831/2000
- 0s - loss: 352638.5939 - mean_squared_error: 352638.5939 - val_loss: 322820.1009 - val_mean_squared_error: 322820.1009
Epoch 1832/2000
- 0s - loss: 352792.9434 - mean_squared_error: 352792.9434 - val_loss: 321974.9352 - val_mean_squared_error: 321974.9352
Epoch 1833/2000
- 0s - loss: 352735.2175 - mean_squared_error: 352735.2175 - val_loss: 321391.9115 - val_mean_squared_error: 321391.9115
Epoch 1834/2000
- 0s - loss: 351935.7235 - mean_squared_error: 351935.7235 - val_loss: 323753.1287 - val_mean_squared_error: 323753.1287
Epoch 1835/2000
- 0s - loss: 352531.7978 - mean_squared_error: 352531.7978 - val_loss: 322526.4762 - val_mean_squared_error: 322526.4762
Epoch 1836/2000
- 0s - loss: 352604.3952 - mean_squared_error: 352604.3952 - val_loss: 321563.6542 - val_mean_squared_error: 321563.6542
Epoch 1837/2000
- 0s - loss: 352392.8832 - mean_squared_error: 352392.8832 - val_loss: 321702.4486 - val_mean_squared_error: 321702.4486
Epoch 1838/2000
- 0s - loss: 352626.8102 - mean_squared_error: 352626.8102 - val_loss: 321687.4584 - val_mean_squared_error: 321687.4584
Epoch 1839/2000
- 0s - loss: 352328.3696 - mean_squared_error: 352328.3696 - val_loss: 322284.7248 - val_mean_squared_error: 322284.7248
Epoch 1840/2000
- 0s - loss: 352630.2977 - mean_squared_error: 352630.2977 - val_loss: 321221.5514 - val_mean_squared_error: 321221.5514
Epoch 1841/2000
- 0s - loss: 352444.8096 - mean_squared_error: 352444.8096 - val_loss: 321824.6473 - val_mean_squared_error: 321824.6473
Epoch 1842/2000
- 0s - loss: 352482.0319 - mean_squared_error: 352482.0319 - val_loss: 321641.6989 - val_mean_squared_error: 321641.6989
Epoch 1843/2000
- 0s - loss: 352372.8971 - mean_squared_error: 352372.8971 - val_loss: 321319.8558 - val_mean_squared_error: 321319.8558
Epoch 1844/2000
- 0s - loss: 352389.4766 - mean_squared_error: 352389.4766 - val_loss: 323707.5949 - val_mean_squared_error: 323707.5949
Epoch 1845/2000
- 0s - loss: 352781.0235 - mean_squared_error: 352781.0235 - val_loss: 321291.5840 - val_mean_squared_error: 321291.5840
Epoch 1846/2000
- 0s - loss: 352106.0627 - mean_squared_error: 352106.0627 - val_loss: 321071.3208 - val_mean_squared_error: 321071.3208
Epoch 1847/2000
- 0s - loss: 351785.5042 - mean_squared_error: 351785.5042 - val_loss: 321158.4504 - val_mean_squared_error: 321158.4504
Epoch 1848/2000
- 0s - loss: 352376.8591 - mean_squared_error: 352376.8591 - val_loss: 321186.0486 - val_mean_squared_error: 321186.0486
Epoch 1849/2000
- 0s - loss: 352178.2893 - mean_squared_error: 352178.2893 - val_loss: 323155.9485 - val_mean_squared_error: 323155.9485
Epoch 1850/2000
- 0s - loss: 352153.0114 - mean_squared_error: 352153.0114 - val_loss: 321153.2629 - val_mean_squared_error: 321153.2629
Epoch 1851/2000
- 0s - loss: 352782.0023 - mean_squared_error: 352782.0023 - val_loss: 321800.5722 - val_mean_squared_error: 321800.5722
Epoch 1852/2000
- 0s - loss: 352016.6540 - mean_squared_error: 352016.6540 - val_loss: 322145.6720 - val_mean_squared_error: 322145.6720
Epoch 1853/2000
- 0s - loss: 352021.9134 - mean_squared_error: 352021.9134 - val_loss: 321694.4788 - val_mean_squared_error: 321694.4788
Epoch 1854/2000
- 0s - loss: 352119.9222 - mean_squared_error: 352119.9222 - val_loss: 321353.8271 - val_mean_squared_error: 321353.8271
Epoch 1855/2000
- 0s - loss: 352235.1926 - mean_squared_error: 352235.1926 - val_loss: 321369.2222 - val_mean_squared_error: 321369.2222
Epoch 1856/2000
- 0s - loss: 352193.0640 - mean_squared_error: 352193.0640 - val_loss: 322583.4591 - val_mean_squared_error: 322583.4591
Epoch 1857/2000
- 0s - loss: 352017.5066 - mean_squared_error: 352017.5066 - val_loss: 322900.6989 - val_mean_squared_error: 322900.6989
Epoch 1858/2000
- 0s - loss: 352078.2558 - mean_squared_error: 352078.2558 - val_loss: 321475.4010 - val_mean_squared_error: 321475.4010
Epoch 1859/2000
- 0s - loss: 352198.4636 - mean_squared_error: 352198.4636 - val_loss: 321521.3116 - val_mean_squared_error: 321521.3116
Epoch 1860/2000
- 0s - loss: 352062.0915 - mean_squared_error: 352062.0915 - val_loss: 321479.3511 - val_mean_squared_error: 321479.3511
Epoch 1861/2000
- 0s - loss: 352102.0045 - mean_squared_error: 352102.0045 - val_loss: 322015.3600 - val_mean_squared_error: 322015.3600
Epoch 1862/2000
- 0s - loss: 352234.2320 - mean_squared_error: 352234.2320 - val_loss: 322595.9791 - val_mean_squared_error: 322595.9791
Epoch 1863/2000
- 0s - loss: 352006.5176 - mean_squared_error: 352006.5176 - val_loss: 321737.5715 - val_mean_squared_error: 321737.5715
Epoch 1864/2000
- 0s - loss: 352435.9867 - mean_squared_error: 352435.9867 - val_loss: 320787.8923 - val_mean_squared_error: 320787.8923
Epoch 1865/2000
- 0s - loss: 352326.2756 - mean_squared_error: 352326.2756 - val_loss: 322110.2077 - val_mean_squared_error: 322110.2077
Epoch 1866/2000
- 0s - loss: 352004.5124 - mean_squared_error: 352004.5124 - val_loss: 321217.3982 - val_mean_squared_error: 321217.3982
Epoch 1867/2000
- 0s - loss: 352266.8707 - mean_squared_error: 352266.8707 - val_loss: 321929.5202 - val_mean_squared_error: 321929.5202
Epoch 1868/2000
- 0s - loss: 352129.3507 - mean_squared_error: 352129.3507 - val_loss: 320808.0614 - val_mean_squared_error: 320808.0614
Epoch 1869/2000
- 0s - loss: 352086.6336 - mean_squared_error: 352086.6336 - val_loss: 323234.1755 - val_mean_squared_error: 323234.1755
Epoch 1870/2000
- 0s - loss: 352069.6200 - mean_squared_error: 352069.6200 - val_loss: 321823.5260 - val_mean_squared_error: 321823.5260
Epoch 1871/2000
- 0s - loss: 351834.2334 - mean_squared_error: 351834.2334 - val_loss: 321119.7924 - val_mean_squared_error: 321119.7924
Epoch 1872/2000
- 0s - loss: 351934.5263 - mean_squared_error: 351934.5263 - val_loss: 320743.5473 - val_mean_squared_error: 320743.5473
Epoch 1873/2000
- 0s - loss: 351754.7197 - mean_squared_error: 351754.7197 - val_loss: 320728.0788 - val_mean_squared_error: 320728.0788
Epoch 1874/2000
- 0s - loss: 351686.1255 - mean_squared_error: 351686.1255 - val_loss: 325863.9035 - val_mean_squared_error: 325863.9035
Epoch 1875/2000
- 0s - loss: 352027.5565 - mean_squared_error: 352027.5565 - val_loss: 322377.7509 - val_mean_squared_error: 322377.7509
Epoch 1876/2000
- 0s - loss: 351773.6168 - mean_squared_error: 351773.6168 - val_loss: 321306.0384 - val_mean_squared_error: 321306.0384
Epoch 1877/2000
- 0s - loss: 351731.8323 - mean_squared_error: 351731.8323 - val_loss: 322280.8299 - val_mean_squared_error: 322280.8299
Epoch 1878/2000
- 0s - loss: 351939.9910 - mean_squared_error: 351939.9910 - val_loss: 320719.5448 - val_mean_squared_error: 320719.5448
Epoch 1879/2000
- 0s - loss: 351811.5054 - mean_squared_error: 351811.5054 - val_loss: 322086.1814 - val_mean_squared_error: 322086.1814
Epoch 1880/2000
- 0s - loss: 351969.0682 - mean_squared_error: 351969.0682 - val_loss: 323696.7555 - val_mean_squared_error: 323696.7555
Epoch 1881/2000
- 0s - loss: 351740.8710 - mean_squared_error: 351740.8710 - val_loss: 321175.8996 - val_mean_squared_error: 321175.8996
Epoch 1882/2000
- 0s - loss: 351783.0421 - mean_squared_error: 351783.0421 - val_loss: 321210.5479 - val_mean_squared_error: 321210.5479
Epoch 1883/2000
- 0s - loss: 351670.6111 - mean_squared_error: 351670.6111 - val_loss: 324955.2986 - val_mean_squared_error: 324955.2986
Epoch 1884/2000
- 0s - loss: 351904.2298 - mean_squared_error: 351904.2298 - val_loss: 320764.6226 - val_mean_squared_error: 320764.6226
Epoch 1885/2000
- 0s - loss: 351816.9915 - mean_squared_error: 351816.9915 - val_loss: 320791.8610 - val_mean_squared_error: 320791.8610
Epoch 1886/2000
- 0s - loss: 351615.2335 - mean_squared_error: 351615.2335 - val_loss: 320851.1270 - val_mean_squared_error: 320851.1270
Epoch 1887/2000
- 0s - loss: 351285.4173 - mean_squared_error: 351285.4173 - val_loss: 322818.1600 - val_mean_squared_error: 322818.1600
Epoch 1888/2000
- 0s - loss: 352008.8270 - mean_squared_error: 352008.8270 - val_loss: 323102.7775 - val_mean_squared_error: 323102.7775
Epoch 1889/2000
- 0s - loss: 351963.0233 - mean_squared_error: 351963.0233 - val_loss: 321013.9407 - val_mean_squared_error: 321013.9407
Epoch 1890/2000
- 0s - loss: 351481.8547 - mean_squared_error: 351481.8547 - val_loss: 321091.4695 - val_mean_squared_error: 321091.4695
Epoch 1891/2000
- 0s - loss: 351505.0111 - mean_squared_error: 351505.0111 - val_loss: 321116.0141 - val_mean_squared_error: 321116.0141
Epoch 1892/2000
- 0s - loss: 351433.4253 - mean_squared_error: 351433.4253 - val_loss: 321061.0411 - val_mean_squared_error: 321061.0411
Epoch 1893/2000
- 0s - loss: 351122.9481 - mean_squared_error: 351122.9481 - val_loss: 320691.0843 - val_mean_squared_error: 320691.0843
Epoch 1894/2000
- 0s - loss: 351521.8679 - mean_squared_error: 351521.8679 - val_loss: 324941.1356 - val_mean_squared_error: 324941.1356
Epoch 1895/2000
- 0s - loss: 351561.7527 - mean_squared_error: 351561.7527 - val_loss: 321182.1784 - val_mean_squared_error: 321182.1784
Epoch 1896/2000
- 0s - loss: 351470.0308 - mean_squared_error: 351470.0308 - val_loss: 323297.2951 - val_mean_squared_error: 323297.2951
Epoch 1897/2000
- 0s - loss: 351745.6374 - mean_squared_error: 351745.6374 - val_loss: 320517.4713 - val_mean_squared_error: 320517.4713
Epoch 1898/2000
- 0s - loss: 351691.2853 - mean_squared_error: 351691.2853 - val_loss: 320498.0968 - val_mean_squared_error: 320498.0968
Epoch 1899/2000
- 0s - loss: 351567.3757 - mean_squared_error: 351567.3757 - val_loss: 320597.0670 - val_mean_squared_error: 320597.0670
Epoch 1900/2000
- 0s - loss: 351300.7174 - mean_squared_error: 351300.7174 - val_loss: 324114.6680 - val_mean_squared_error: 324114.6680
Epoch 1901/2000
- 0s - loss: 351173.0977 - mean_squared_error: 351173.0977 - val_loss: 321130.5498 - val_mean_squared_error: 321130.5498
Epoch 1902/2000
- 0s - loss: 351405.3581 - mean_squared_error: 351405.3581 - val_loss: 321523.2287 - val_mean_squared_error: 321523.2287
Epoch 1903/2000
- 0s - loss: 351206.5453 - mean_squared_error: 351206.5453 - val_loss: 320541.2431 - val_mean_squared_error: 320541.2431
Epoch 1904/2000
- 0s - loss: 351668.0912 - mean_squared_error: 351668.0912 - val_loss: 320546.0671 - val_mean_squared_error: 320546.0671
Epoch 1905/2000
- 0s - loss: 351069.9819 - mean_squared_error: 351069.9819 - val_loss: 320459.3314 - val_mean_squared_error: 320459.3314
Epoch 1906/2000
- 0s - loss: 351435.6701 - mean_squared_error: 351435.6701 - val_loss: 321989.0115 - val_mean_squared_error: 321989.0115
Epoch 1907/2000
- 0s - loss: 351298.0716 - mean_squared_error: 351298.0716 - val_loss: 322274.4590 - val_mean_squared_error: 322274.4590
Epoch 1908/2000
- 0s - loss: 350774.8583 - mean_squared_error: 350774.8583 - val_loss: 320461.4206 - val_mean_squared_error: 320461.4206
Epoch 1909/2000
- 0s - loss: 351546.8358 - mean_squared_error: 351546.8358 - val_loss: 322772.2442 - val_mean_squared_error: 322772.2442
Epoch 1910/2000
- 0s - loss: 351531.8571 - mean_squared_error: 351531.8571 - val_loss: 320255.2415 - val_mean_squared_error: 320255.2415
Epoch 1911/2000
- 0s - loss: 351123.9902 - mean_squared_error: 351123.9902 - val_loss: 323927.2046 - val_mean_squared_error: 323927.2046
Epoch 1912/2000
- 0s - loss: 351175.4219 - mean_squared_error: 351175.4219 - val_loss: 322185.1594 - val_mean_squared_error: 322185.1594
Epoch 1913/2000
- 0s - loss: 351124.5860 - mean_squared_error: 351124.5860 - val_loss: 320269.5490 - val_mean_squared_error: 320269.5490
Epoch 1914/2000
- 0s - loss: 351164.6861 - mean_squared_error: 351164.6861 - val_loss: 320922.3566 - val_mean_squared_error: 320922.3566
Epoch 1915/2000
- 0s - loss: 351430.4632 - mean_squared_error: 351430.4632 - val_loss: 321206.3645 - val_mean_squared_error: 321206.3645
Epoch 1916/2000
- 0s - loss: 351039.9810 - mean_squared_error: 351039.9810 - val_loss: 322146.4838 - val_mean_squared_error: 322146.4838
Epoch 1917/2000
- 0s - loss: 351092.1443 - mean_squared_error: 351092.1443 - val_loss: 320477.6637 - val_mean_squared_error: 320477.6637
Epoch 1918/2000
- 0s - loss: 351279.6311 - mean_squared_error: 351279.6311 - val_loss: 322849.2993 - val_mean_squared_error: 322849.2993
Epoch 1919/2000
- 0s - loss: 351378.9222 - mean_squared_error: 351378.9222 - val_loss: 320415.2793 - val_mean_squared_error: 320415.2793
Epoch 1920/2000
- 0s - loss: 351077.6502 - mean_squared_error: 351077.6502 - val_loss: 320414.5563 - val_mean_squared_error: 320414.5563
Epoch 1921/2000
- 0s - loss: 351523.3945 - mean_squared_error: 351523.3945 - val_loss: 321847.9682 - val_mean_squared_error: 321847.9682
Epoch 1922/2000
- 0s - loss: 351072.6680 - mean_squared_error: 351072.6680 - val_loss: 321248.8032 - val_mean_squared_error: 321248.8032
Epoch 1923/2000
- 0s - loss: 351459.1636 - mean_squared_error: 351459.1636 - val_loss: 321194.2757 - val_mean_squared_error: 321194.2757
Epoch 1924/2000
- 0s - loss: 350877.2161 - mean_squared_error: 350877.2161 - val_loss: 320426.4567 - val_mean_squared_error: 320426.4567
Epoch 1925/2000
- 0s - loss: 350936.2435 - mean_squared_error: 350936.2435 - val_loss: 322513.9072 - val_mean_squared_error: 322513.9072
Epoch 1926/2000
- 0s - loss: 351073.9743 - mean_squared_error: 351073.9743 - val_loss: 320405.1168 - val_mean_squared_error: 320405.1168
Epoch 1927/2000
- 0s - loss: 351355.3434 - mean_squared_error: 351355.3434 - val_loss: 320018.8288 - val_mean_squared_error: 320018.8288
Epoch 1928/2000
- 0s - loss: 351079.9940 - mean_squared_error: 351079.9940 - val_loss: 320791.3080 - val_mean_squared_error: 320791.3080
Epoch 1929/2000
- 0s - loss: 351064.3151 - mean_squared_error: 351064.3151 - val_loss: 320712.5592 - val_mean_squared_error: 320712.5592
Epoch 1930/2000
- 0s - loss: 351300.7137 - mean_squared_error: 351300.7137 - val_loss: 321289.1198 - val_mean_squared_error: 321289.1198
Epoch 1931/2000
- 0s - loss: 351233.0456 - mean_squared_error: 351233.0456 - val_loss: 322679.0501 - val_mean_squared_error: 322679.0501
Epoch 1932/2000
- 0s - loss: 350893.3236 - mean_squared_error: 350893.3236 - val_loss: 320317.3456 - val_mean_squared_error: 320317.3456
Epoch 1933/2000
- 0s - loss: 351329.4404 - mean_squared_error: 351329.4404 - val_loss: 319852.4713 - val_mean_squared_error: 319852.4713
Epoch 1934/2000
- 0s - loss: 351124.6956 - mean_squared_error: 351124.6956 - val_loss: 320436.1364 - val_mean_squared_error: 320436.1364
Epoch 1935/2000
- 0s - loss: 351053.7903 - mean_squared_error: 351053.7903 - val_loss: 320834.8588 - val_mean_squared_error: 320834.8588
Epoch 1936/2000
- 0s - loss: 350984.9909 - mean_squared_error: 350984.9909 - val_loss: 321249.0250 - val_mean_squared_error: 321249.0250
Epoch 1937/2000
- 0s - loss: 350841.7996 - mean_squared_error: 350841.7996 - val_loss: 320661.3310 - val_mean_squared_error: 320661.3310
Epoch 1938/2000
- 0s - loss: 350720.7031 - mean_squared_error: 350720.7031 - val_loss: 320589.8654 - val_mean_squared_error: 320589.8654
Epoch 1939/2000
- 0s - loss: 350983.4347 - mean_squared_error: 350983.4347 - val_loss: 320438.1442 - val_mean_squared_error: 320438.1442
Epoch 1940/2000
- 0s - loss: 350860.4392 - mean_squared_error: 350860.4392 - val_loss: 321121.9078 - val_mean_squared_error: 321121.9078
Epoch 1941/2000
- 0s - loss: 351001.5372 - mean_squared_error: 351001.5372 - val_loss: 320003.6929 - val_mean_squared_error: 320003.6929
Epoch 1942/2000
- 0s - loss: 350936.1459 - mean_squared_error: 350936.1459 - val_loss: 320647.4402 - val_mean_squared_error: 320647.4402
Epoch 1943/2000
- 0s - loss: 350834.0426 - mean_squared_error: 350834.0426 - val_loss: 320384.9495 - val_mean_squared_error: 320384.9495
Epoch 1944/2000
- 0s - loss: 351162.9750 - mean_squared_error: 351162.9750 - val_loss: 322697.6413 - val_mean_squared_error: 322697.6413
Epoch 1945/2000
- 0s - loss: 351042.0928 - mean_squared_error: 351042.0928 - val_loss: 320229.0246 - val_mean_squared_error: 320229.0246
Epoch 1946/2000
- 1s - loss: 350967.1519 - mean_squared_error: 350967.1519 - val_loss: 321109.6796 - val_mean_squared_error: 321109.6796
Epoch 1947/2000
- 1s - loss: 351546.0674 - mean_squared_error: 351546.0674 - val_loss: 319761.1340 - val_mean_squared_error: 319761.1340
Epoch 1948/2000
- 0s - loss: 351032.9363 - mean_squared_error: 351032.9363 - val_loss: 321014.5154 - val_mean_squared_error: 321014.5154
Epoch 1949/2000
- 1s - loss: 350831.0772 - mean_squared_error: 350831.0772 - val_loss: 320220.1645 - val_mean_squared_error: 320220.1645
Epoch 1950/2000
- 0s - loss: 350525.6807 - mean_squared_error: 350525.6807 - val_loss: 321441.4327 - val_mean_squared_error: 321441.4327
Epoch 1951/2000
- 0s - loss: 350881.6454 - mean_squared_error: 350881.6454 - val_loss: 320592.7997 - val_mean_squared_error: 320592.7997
Epoch 1952/2000
- 0s - loss: 350383.6098 - mean_squared_error: 350383.6098 - val_loss: 322400.0443 - val_mean_squared_error: 322400.0443
Epoch 1953/2000
- 0s - loss: 350707.1438 - mean_squared_error: 350707.1438 - val_loss: 319757.0388 - val_mean_squared_error: 319757.0388
Epoch 1954/2000
- 0s - loss: 350510.8410 - mean_squared_error: 350510.8410 - val_loss: 321124.5681 - val_mean_squared_error: 321124.5681
Epoch 1955/2000
- 0s - loss: 350382.6248 - mean_squared_error: 350382.6248 - val_loss: 321917.0947 - val_mean_squared_error: 321917.0947
Epoch 1956/2000
- 0s - loss: 350494.4437 - mean_squared_error: 350494.4437 - val_loss: 323771.4122 - val_mean_squared_error: 323771.4122
Epoch 1957/2000
- 0s - loss: 350762.2462 - mean_squared_error: 350762.2462 - val_loss: 319887.6764 - val_mean_squared_error: 319887.6764
Epoch 1958/2000
- 0s - loss: 350812.8616 - mean_squared_error: 350812.8616 - val_loss: 319785.3546 - val_mean_squared_error: 319785.3546
Epoch 1959/2000
- 0s - loss: 350633.5645 - mean_squared_error: 350633.5645 - val_loss: 320639.5500 - val_mean_squared_error: 320639.5500
Epoch 1960/2000
- 0s - loss: 350431.9455 - mean_squared_error: 350431.9455 - val_loss: 320044.3539 - val_mean_squared_error: 320044.3539
Epoch 1961/2000
- 0s - loss: 350607.4654 - mean_squared_error: 350607.4654 - val_loss: 320627.9426 - val_mean_squared_error: 320627.9426
Epoch 1962/2000
- 0s - loss: 350769.9184 - mean_squared_error: 350769.9184 - val_loss: 320445.9118 - val_mean_squared_error: 320445.9118
Epoch 1963/2000
- 0s - loss: 350721.9007 - mean_squared_error: 350721.9007 - val_loss: 320749.6331 - val_mean_squared_error: 320749.6331
Epoch 1964/2000
- 0s - loss: 350791.8435 - mean_squared_error: 350791.8435 - val_loss: 320953.2111 - val_mean_squared_error: 320953.2111
Epoch 1965/2000
- 0s - loss: 350626.2471 - mean_squared_error: 350626.2471 - val_loss: 320379.1204 - val_mean_squared_error: 320379.1204
Epoch 1966/2000
- 0s - loss: 350645.8384 - mean_squared_error: 350645.8384 - val_loss: 321258.9025 - val_mean_squared_error: 321258.9025
Epoch 1967/2000
- 0s - loss: 351144.3000 - mean_squared_error: 351144.3000 - val_loss: 319555.7377 - val_mean_squared_error: 319555.7377
Epoch 1968/2000
- 0s - loss: 350257.5325 - mean_squared_error: 350257.5325 - val_loss: 320498.8982 - val_mean_squared_error: 320498.8982
Epoch 1969/2000
- 0s - loss: 350440.9468 - mean_squared_error: 350440.9468 - val_loss: 323353.8991 - val_mean_squared_error: 323353.8991
Epoch 1970/2000
- 0s - loss: 350514.8672 - mean_squared_error: 350514.8672 - val_loss: 319926.7191 - val_mean_squared_error: 319926.7191
Epoch 1971/2000
- 0s - loss: 350476.5234 - mean_squared_error: 350476.5234 - val_loss: 320403.7104 - val_mean_squared_error: 320403.7104
Epoch 1972/2000
- 0s - loss: 350614.9112 - mean_squared_error: 350614.9112 - val_loss: 320656.1458 - val_mean_squared_error: 320656.1458
Epoch 1973/2000
- 0s - loss: 350340.0376 - mean_squared_error: 350340.0376 - val_loss: 323562.8329 - val_mean_squared_error: 323562.8329
Epoch 1974/2000
- 0s - loss: 350855.2276 - mean_squared_error: 350855.2276 - val_loss: 319600.7327 - val_mean_squared_error: 319600.7327
Epoch 1975/2000
- 0s - loss: 350561.9088 - mean_squared_error: 350561.9088 - val_loss: 321137.1200 - val_mean_squared_error: 321137.1200
Epoch 1976/2000
- 0s - loss: 350554.1135 - mean_squared_error: 350554.1135 - val_loss: 319576.2050 - val_mean_squared_error: 319576.2050
Epoch 1977/2000
- 0s - loss: 350576.2284 - mean_squared_error: 350576.2284 - val_loss: 319929.7035 - val_mean_squared_error: 319929.7035
Epoch 1978/2000
- 0s - loss: 350541.0335 - mean_squared_error: 350541.0335 - val_loss: 319699.2241 - val_mean_squared_error: 319699.2241
Epoch 1979/2000
- 0s - loss: 350542.8354 - mean_squared_error: 350542.8354 - val_loss: 320522.0850 - val_mean_squared_error: 320522.0850
Epoch 1980/2000
- 0s - loss: 350310.6930 - mean_squared_error: 350310.6930 - val_loss: 321860.9097 - val_mean_squared_error: 321860.9097
Epoch 1981/2000
- 0s - loss: 350367.3628 - mean_squared_error: 350367.3628 - val_loss: 322932.4098 - val_mean_squared_error: 322932.4098
Epoch 1982/2000
- 0s - loss: 350613.5599 - mean_squared_error: 350613.5599 - val_loss: 320085.8123 - val_mean_squared_error: 320085.8123
Epoch 1983/2000
- 0s - loss: 350550.4906 - mean_squared_error: 350550.4906 - val_loss: 321715.1233 - val_mean_squared_error: 321715.1233
Epoch 1984/2000
- 0s - loss: 350098.3904 - mean_squared_error: 350098.3904 - val_loss: 319653.5809 - val_mean_squared_error: 319653.5809
Epoch 1985/2000
- 0s - loss: 350215.2669 - mean_squared_error: 350215.2669 - val_loss: 319889.6822 - val_mean_squared_error: 319889.6822
Epoch 1986/2000
- 0s - loss: 350394.0994 - mean_squared_error: 350394.0994 - val_loss: 320383.7723 - val_mean_squared_error: 320383.7723
Epoch 1987/2000
- 0s - loss: 350067.7060 - mean_squared_error: 350067.7060 - val_loss: 320083.8967 - val_mean_squared_error: 320083.8967
Epoch 1988/2000
- 0s - loss: 349942.0462 - mean_squared_error: 349942.0462 - val_loss: 320788.4456 - val_mean_squared_error: 320788.4456
Epoch 1989/2000
- 0s - loss: 350594.1286 - mean_squared_error: 350594.1286 - val_loss: 320672.2185 - val_mean_squared_error: 320672.2185
Epoch 1990/2000
- 0s - loss: 350586.9137 - mean_squared_error: 350586.9137 - val_loss: 320443.1261 - val_mean_squared_error: 320443.1261
Epoch 1991/2000
- 0s - loss: 350447.7632 - mean_squared_error: 350447.7632 - val_loss: 319521.4387 - val_mean_squared_error: 319521.4387
Epoch 1992/2000
- 0s - loss: 350198.1232 - mean_squared_error: 350198.1232 - val_loss: 319705.7904 - val_mean_squared_error: 319705.7904
Epoch 1993/2000
- 0s - loss: 350177.6373 - mean_squared_error: 350177.6373 - val_loss: 319399.6656 - val_mean_squared_error: 319399.6656
Epoch 1994/2000
- 0s - loss: 349822.2746 - mean_squared_error: 349822.2746 - val_loss: 319906.7587 - val_mean_squared_error: 319906.7587
Epoch 1995/2000
- 0s - loss: 349979.3041 - mean_squared_error: 349979.3041 - val_loss: 320456.3252 - val_mean_squared_error: 320456.3252
Epoch 1996/2000
- 0s - loss: 349674.5740 - mean_squared_error: 349674.5740 - val_loss: 320019.5364 - val_mean_squared_error: 320019.5364
Epoch 1997/2000
- 0s - loss: 350329.6704 - mean_squared_error: 350329.6704 - val_loss: 321159.2947 - val_mean_squared_error: 321159.2947
Epoch 1998/2000
- 0s - loss: 350249.9685 - mean_squared_error: 350249.9685 - val_loss: 320483.8665 - val_mean_squared_error: 320483.8665
Epoch 1999/2000
- 0s - loss: 349857.2837 - mean_squared_error: 349857.2837 - val_loss: 319652.7423 - val_mean_squared_error: 319652.7423
Epoch 2000/2000
- 0s - loss: 350730.7542 - mean_squared_error: 350730.7542 - val_loss: 319270.1511 - val_mean_squared_error: 319270.1511
32/13485 [..............................] - ETA: 0s
3840/13485 [=======>......................] - ETA: 0s
7584/13485 [===============>..............] - ETA: 0s
11392/13485 [========================>.....] - ETA: 0s
13485/13485 [==============================] - 0s 13us/step
root mean_squared_error: 595.088727
Would you look at that?!
- We break $1000 RMSE around epoch 112
- $900 around epoch 220
- $800 around epoch 450
- By around epoch 2000, my RMSE is < $600
...
Same theory; different activation function. Huge difference
Multilayer Networks
If a single-layer perceptron network learns the importance of different combinations of features in the data...
What would another network learn if it had a second (hidden) layer of neurons?
It depends on how we train the network. We'll talk in the next section about how this training works, but the general idea is that we still work backward from the error gradient.
That is, the last layer learns from error in the output; the second-to-last layer learns from error transmitted through that last layer, etc. It's a touch hand-wavy for now, but we'll make it more concrete later.
Given this approach, we can say that:
- The second (hidden) layer is learning features composed of activations in the first (hidden) layer
- The first (hidden) layer is learning feature weights that enable the second layer to perform best
- Why? Earlier, the first hidden layer just learned feature weights because that's how it was judged
- Now, the first hidden layer is judged on the error in the second layer, so it learns to contribute to that second layer
- The second layer is learning new features that aren't explicit in the data, and is teaching the first layer to supply it with the necessary information to compose these new features
So instead of just feature weighting and combining, we have new feature learning!
This concept is the foundation of the "Deep Feed-Forward Network"

Let's try it!
Add a layer to your Keras network, perhaps another 20 neurons, and see how the training goes.
if you get stuck, there is a solution in the Keras-DFFN notebook
I'm getting RMSE < $1000 by epoch 35 or so
< $800 by epoch 90
In this configuration, mine makes progress to around 700 epochs or so and then stalls with RMSE around $560
Our network has "gone meta"
It's now able to exceed where a simple decision tree can go, because it can create new features and then split on those
Congrats! You have built your first deep-learning model!
So does that mean we can just keep adding more layers and solve anything?
Well, theoretically maybe ... try reconfiguring your network, watch the training, and see what happens.

ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
import pandas as pd
input_file = "/dbfs/databricks-datasets/Rdatasets/data-001/csv/ggplot2/diamonds.csv"
df = pd.read_csv(input_file, header = 0)
df.drop(df.columns[0], axis=1, inplace=True)
df = pd.get_dummies(df, prefix=['cut_', 'color_', 'clarity_'])
y = df.iloc[:,3:4].as_matrix().flatten()
y.flatten()
X = df.drop(df.columns[3], axis=1).as_matrix()
np.shape(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
model = Sequential()
model.add(Dense(30, input_dim=26, kernel_initializer='normal', activation='relu'))
model.add(Dense(20, kernel_initializer='normal', activation='relu')) # <--- CHANGE IS HERE
model.add(Dense(1, kernel_initializer='normal', activation='linear'))
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mean_squared_error'])
history = model.fit(X_train, y_train, epochs=1000, batch_size=100, validation_split=0.1, verbose=2)
scores = model.evaluate(X_test, y_test)
print("\nroot %s: %f" % (model.metrics_names[1], np.sqrt(scores[1])))
Using TensorFlow backend.
/local_disk0/tmp/1612952202226-0/PythonShell.py:12: FutureWarning: Method .as_matrix will be removed in a future version. Use .values instead.
import subprocess
/local_disk0/tmp/1612952202226-0/PythonShell.py:15: FutureWarning: Method .as_matrix will be removed in a future version. Use .values instead.
import traceback
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 36409 samples, validate on 4046 samples
Epoch 1/1000
- 1s - loss: 27848997.3139 - mean_squared_error: 27848997.3139 - val_loss: 19941055.5610 - val_mean_squared_error: 19941055.5610
Epoch 2/1000
- 0s - loss: 15721444.7310 - mean_squared_error: 15721444.7310 - val_loss: 15635870.6471 - val_mean_squared_error: 15635870.6471
Epoch 3/1000
- 0s - loss: 14878335.3089 - mean_squared_error: 14878335.3089 - val_loss: 15269761.0084 - val_mean_squared_error: 15269761.0084
Epoch 4/1000
- 0s - loss: 14444641.0725 - mean_squared_error: 14444641.0725 - val_loss: 14715442.8384 - val_mean_squared_error: 14715442.8384
Epoch 5/1000
- 0s - loss: 13770065.9625 - mean_squared_error: 13770065.9625 - val_loss: 13880356.9006 - val_mean_squared_error: 13880356.9006
Epoch 6/1000
- 0s - loss: 12818473.6246 - mean_squared_error: 12818473.6246 - val_loss: 12705441.9807 - val_mean_squared_error: 12705441.9807
Epoch 7/1000
- 0s - loss: 11430221.0811 - mean_squared_error: 11430221.0811 - val_loss: 10969834.3841 - val_mean_squared_error: 10969834.3841
Epoch 8/1000
- 0s - loss: 9393624.8908 - mean_squared_error: 9393624.8908 - val_loss: 8498211.5195 - val_mean_squared_error: 8498211.5195
Epoch 9/1000
- 0s - loss: 6862340.6293 - mean_squared_error: 6862340.6293 - val_loss: 5880691.8688 - val_mean_squared_error: 5880691.8688
Epoch 10/1000
- 0s - loss: 4776505.1199 - mean_squared_error: 4776505.1199 - val_loss: 4203533.3239 - val_mean_squared_error: 4203533.3239
Epoch 11/1000
- 0s - loss: 3611367.8372 - mean_squared_error: 3611367.8372 - val_loss: 3243258.9528 - val_mean_squared_error: 3243258.9528
Epoch 12/1000
- 0s - loss: 2951622.9117 - mean_squared_error: 2951622.9117 - val_loss: 2672585.9130 - val_mean_squared_error: 2672585.9130
Epoch 13/1000
- 0s - loss: 2545050.5128 - mean_squared_error: 2545050.5128 - val_loss: 2280816.6159 - val_mean_squared_error: 2280816.6159
Epoch 14/1000
- 0s - loss: 2262868.8862 - mean_squared_error: 2262868.8862 - val_loss: 2000101.9238 - val_mean_squared_error: 2000101.9238
Epoch 15/1000
- 0s - loss: 2053373.8769 - mean_squared_error: 2053373.8769 - val_loss: 1783650.4861 - val_mean_squared_error: 1783650.4861
Epoch 16/1000
- 0s - loss: 1891749.5903 - mean_squared_error: 1891749.5903 - val_loss: 1652615.4016 - val_mean_squared_error: 1652615.4016
Epoch 17/1000
- 0s - loss: 1761506.1582 - mean_squared_error: 1761506.1582 - val_loss: 1479201.0310 - val_mean_squared_error: 1479201.0310
Epoch 18/1000
- 0s - loss: 1652759.2415 - mean_squared_error: 1652759.2415 - val_loss: 1362899.9525 - val_mean_squared_error: 1362899.9525
Epoch 19/1000
- 0s - loss: 1564938.7439 - mean_squared_error: 1564938.7439 - val_loss: 1280093.5768 - val_mean_squared_error: 1280093.5768
Epoch 20/1000
- 1s - loss: 1487247.7714 - mean_squared_error: 1487247.7714 - val_loss: 1197266.3815 - val_mean_squared_error: 1197266.3815
Epoch 21/1000
- 0s - loss: 1425106.5209 - mean_squared_error: 1425106.5209 - val_loss: 1129568.2545 - val_mean_squared_error: 1129568.2545
Epoch 22/1000
- 0s - loss: 1371662.6921 - mean_squared_error: 1371662.6921 - val_loss: 1082736.0722 - val_mean_squared_error: 1082736.0722
Epoch 23/1000
- 0s - loss: 1325085.8587 - mean_squared_error: 1325085.8587 - val_loss: 1025223.1728 - val_mean_squared_error: 1025223.1728
Epoch 24/1000
- 0s - loss: 1285938.1454 - mean_squared_error: 1285938.1454 - val_loss: 987946.3071 - val_mean_squared_error: 987946.3071
Epoch 25/1000
- 0s - loss: 1251586.8131 - mean_squared_error: 1251586.8131 - val_loss: 960801.6510 - val_mean_squared_error: 960801.6510
Epoch 26/1000
- 0s - loss: 1221759.4081 - mean_squared_error: 1221759.4081 - val_loss: 989834.2255 - val_mean_squared_error: 989834.2255
Epoch 27/1000
- 0s - loss: 1196454.2777 - mean_squared_error: 1196454.2777 - val_loss: 894349.4676 - val_mean_squared_error: 894349.4676
Epoch 28/1000
- 0s - loss: 1175772.0771 - mean_squared_error: 1175772.0771 - val_loss: 871894.4783 - val_mean_squared_error: 871894.4783
Epoch 29/1000
- 0s - loss: 1154657.9466 - mean_squared_error: 1154657.9466 - val_loss: 857967.9547 - val_mean_squared_error: 857967.9547
Epoch 30/1000
- 0s - loss: 1137330.4296 - mean_squared_error: 1137330.4296 - val_loss: 830822.8925 - val_mean_squared_error: 830822.8925
Epoch 31/1000
- 0s - loss: 1118996.4988 - mean_squared_error: 1118996.4988 - val_loss: 824682.6183 - val_mean_squared_error: 824682.6183
Epoch 32/1000
- 0s - loss: 1106886.6546 - mean_squared_error: 1106886.6546 - val_loss: 804009.3922 - val_mean_squared_error: 804009.3922
Epoch 33/1000
- 0s - loss: 1092238.8060 - mean_squared_error: 1092238.8060 - val_loss: 790091.7014 - val_mean_squared_error: 790091.7014
Epoch 34/1000
- 0s - loss: 1079786.7414 - mean_squared_error: 1079786.7414 - val_loss: 775591.1924 - val_mean_squared_error: 775591.1924
Epoch 35/1000
- 0s - loss: 1069167.4304 - mean_squared_error: 1069167.4304 - val_loss: 763125.2484 - val_mean_squared_error: 763125.2484
Epoch 36/1000
- 0s - loss: 1059513.6255 - mean_squared_error: 1059513.6255 - val_loss: 755934.6476 - val_mean_squared_error: 755934.6476
Epoch 37/1000
- 0s - loss: 1047650.8134 - mean_squared_error: 1047650.8134 - val_loss: 743270.3341 - val_mean_squared_error: 743270.3341
Epoch 38/1000
- 0s - loss: 1040286.9653 - mean_squared_error: 1040286.9653 - val_loss: 736469.8614 - val_mean_squared_error: 736469.8614
Epoch 39/1000
- 0s - loss: 1029818.0804 - mean_squared_error: 1029818.0804 - val_loss: 728033.5843 - val_mean_squared_error: 728033.5843
Epoch 40/1000
- 0s - loss: 1019190.3500 - mean_squared_error: 1019190.3500 - val_loss: 718948.9588 - val_mean_squared_error: 718948.9588
Epoch 41/1000
- 0s - loss: 1016885.7825 - mean_squared_error: 1016885.7825 - val_loss: 710640.1856 - val_mean_squared_error: 710640.1856
Epoch 42/1000
- 0s - loss: 1004592.2712 - mean_squared_error: 1004592.2712 - val_loss: 746145.3573 - val_mean_squared_error: 746145.3573
Epoch 43/1000
- 0s - loss: 997372.0076 - mean_squared_error: 997372.0076 - val_loss: 697639.3794 - val_mean_squared_error: 697639.3794
Epoch 44/1000
- 0s - loss: 991401.2183 - mean_squared_error: 991401.2183 - val_loss: 692106.8087 - val_mean_squared_error: 692106.8087
Epoch 45/1000
- 0s - loss: 983574.4552 - mean_squared_error: 983574.4552 - val_loss: 686729.2726 - val_mean_squared_error: 686729.2726
Epoch 46/1000
- 0s - loss: 975824.9971 - mean_squared_error: 975824.9971 - val_loss: 680648.6108 - val_mean_squared_error: 680648.6108
Epoch 47/1000
- 0s - loss: 970501.5993 - mean_squared_error: 970501.5993 - val_loss: 694138.4560 - val_mean_squared_error: 694138.4560
Epoch 48/1000
- 0s - loss: 963974.9468 - mean_squared_error: 963974.9468 - val_loss: 670440.0686 - val_mean_squared_error: 670440.0686
Epoch 49/1000
- 0s - loss: 957421.3169 - mean_squared_error: 957421.3169 - val_loss: 664542.6438 - val_mean_squared_error: 664542.6438
Epoch 50/1000
- 0s - loss: 949259.1143 - mean_squared_error: 949259.1143 - val_loss: 659279.1652 - val_mean_squared_error: 659279.1652
Epoch 51/1000
- 0s - loss: 947019.5684 - mean_squared_error: 947019.5684 - val_loss: 659463.5773 - val_mean_squared_error: 659463.5773
Epoch 52/1000
- 0s - loss: 940984.1682 - mean_squared_error: 940984.1682 - val_loss: 657588.1767 - val_mean_squared_error: 657588.1767
Epoch 53/1000
- 0s - loss: 936560.8663 - mean_squared_error: 936560.8663 - val_loss: 654709.2946 - val_mean_squared_error: 654709.2946
Epoch 54/1000
- 0s - loss: 929876.5311 - mean_squared_error: 929876.5311 - val_loss: 649337.2466 - val_mean_squared_error: 649337.2466
Epoch 55/1000
- 0s - loss: 924841.0342 - mean_squared_error: 924841.0342 - val_loss: 643723.5302 - val_mean_squared_error: 643723.5302
Epoch 56/1000
- 0s - loss: 918614.3575 - mean_squared_error: 918614.3575 - val_loss: 644705.0716 - val_mean_squared_error: 644705.0716
Epoch 57/1000
- 0s - loss: 915670.1215 - mean_squared_error: 915670.1215 - val_loss: 636346.6608 - val_mean_squared_error: 636346.6608
Epoch 58/1000
- 0s - loss: 909534.4711 - mean_squared_error: 909534.4711 - val_loss: 647823.2318 - val_mean_squared_error: 647823.2318
Epoch 59/1000
- 0s - loss: 904965.2166 - mean_squared_error: 904965.2166 - val_loss: 628485.2156 - val_mean_squared_error: 628485.2156
Epoch 60/1000
- 0s - loss: 902425.5051 - mean_squared_error: 902425.5051 - val_loss: 622688.3500 - val_mean_squared_error: 622688.3500
Epoch 61/1000
- 0s - loss: 897871.7921 - mean_squared_error: 897871.7921 - val_loss: 624881.6728 - val_mean_squared_error: 624881.6728
Epoch 62/1000
- 0s - loss: 894782.2215 - mean_squared_error: 894782.2215 - val_loss: 627024.9350 - val_mean_squared_error: 627024.9350
Epoch 63/1000
- 0s - loss: 889052.8088 - mean_squared_error: 889052.8088 - val_loss: 617370.9787 - val_mean_squared_error: 617370.9787
Epoch 64/1000
- 0s - loss: 884556.7834 - mean_squared_error: 884556.7834 - val_loss: 612704.8653 - val_mean_squared_error: 612704.8653
Epoch 65/1000
- 0s - loss: 881022.9232 - mean_squared_error: 881022.9232 - val_loss: 610227.8523 - val_mean_squared_error: 610227.8523
Epoch 66/1000
- 0s - loss: 878086.1132 - mean_squared_error: 878086.1132 - val_loss: 609204.8112 - val_mean_squared_error: 609204.8112
Epoch 67/1000
- 0s - loss: 871305.0931 - mean_squared_error: 871305.0931 - val_loss: 619089.4905 - val_mean_squared_error: 619089.4905
Epoch 68/1000
- 0s - loss: 868253.8074 - mean_squared_error: 868253.8074 - val_loss: 603386.7772 - val_mean_squared_error: 603386.7772
Epoch 69/1000
- 0s - loss: 866479.5393 - mean_squared_error: 866479.5393 - val_loss: 602248.2999 - val_mean_squared_error: 602248.2999
Epoch 70/1000
- 0s - loss: 861741.1125 - mean_squared_error: 861741.1125 - val_loss: 600190.8303 - val_mean_squared_error: 600190.8303
Epoch 71/1000
- 0s - loss: 858456.8250 - mean_squared_error: 858456.8250 - val_loss: 599150.2672 - val_mean_squared_error: 599150.2672
Epoch 72/1000
- 0s - loss: 852272.1151 - mean_squared_error: 852272.1151 - val_loss: 631487.3969 - val_mean_squared_error: 631487.3969
Epoch 73/1000
- 0s - loss: 849696.0093 - mean_squared_error: 849696.0093 - val_loss: 594680.5698 - val_mean_squared_error: 594680.5698
Epoch 74/1000
- 0s - loss: 846110.9814 - mean_squared_error: 846110.9814 - val_loss: 592059.0109 - val_mean_squared_error: 592059.0109
Epoch 75/1000
- 0s - loss: 843963.9626 - mean_squared_error: 843963.9626 - val_loss: 596066.5905 - val_mean_squared_error: 596066.5905
Epoch 76/1000
- 0s - loss: 839582.4143 - mean_squared_error: 839582.4143 - val_loss: 590086.6497 - val_mean_squared_error: 590086.6497
Epoch 77/1000
- 0s - loss: 836005.5393 - mean_squared_error: 836005.5393 - val_loss: 585910.5458 - val_mean_squared_error: 585910.5458
Epoch 78/1000
- 0s - loss: 834314.4576 - mean_squared_error: 834314.4576 - val_loss: 585601.5675 - val_mean_squared_error: 585601.5675
Epoch 79/1000
- 0s - loss: 830026.6519 - mean_squared_error: 830026.6519 - val_loss: 583452.0687 - val_mean_squared_error: 583452.0687
Epoch 80/1000
- 0s - loss: 827575.0680 - mean_squared_error: 827575.0680 - val_loss: 581430.0357 - val_mean_squared_error: 581430.0357
Epoch 81/1000
- 0s - loss: 824253.8759 - mean_squared_error: 824253.8759 - val_loss: 582939.6549 - val_mean_squared_error: 582939.6549
Epoch 82/1000
- 0s - loss: 822642.5272 - mean_squared_error: 822642.5272 - val_loss: 581081.3391 - val_mean_squared_error: 581081.3391
Epoch 83/1000
- 0s - loss: 815923.2499 - mean_squared_error: 815923.2499 - val_loss: 576631.4536 - val_mean_squared_error: 576631.4536
Epoch 84/1000
- 1s - loss: 815410.5528 - mean_squared_error: 815410.5528 - val_loss: 575940.6918 - val_mean_squared_error: 575940.6918
Epoch 85/1000
- 1s - loss: 812062.3854 - mean_squared_error: 812062.3854 - val_loss: 573674.8378 - val_mean_squared_error: 573674.8378
Epoch 86/1000
- 1s - loss: 806719.4352 - mean_squared_error: 806719.4352 - val_loss: 615332.8055 - val_mean_squared_error: 615332.8055
Epoch 87/1000
- 1s - loss: 805988.4498 - mean_squared_error: 805988.4498 - val_loss: 572746.6689 - val_mean_squared_error: 572746.6689
Epoch 88/1000
- 1s - loss: 803310.7549 - mean_squared_error: 803310.7549 - val_loss: 581164.5382 - val_mean_squared_error: 581164.5382
Epoch 89/1000
- 1s - loss: 798728.6701 - mean_squared_error: 798728.6701 - val_loss: 568163.1727 - val_mean_squared_error: 568163.1727
Epoch 90/1000
- 1s - loss: 796360.8602 - mean_squared_error: 796360.8602 - val_loss: 566627.2496 - val_mean_squared_error: 566627.2496
Epoch 91/1000
- 1s - loss: 794783.4675 - mean_squared_error: 794783.4675 - val_loss: 567482.9140 - val_mean_squared_error: 567482.9140
Epoch 92/1000
- 1s - loss: 791396.5386 - mean_squared_error: 791396.5386 - val_loss: 567086.7926 - val_mean_squared_error: 567086.7926
Epoch 93/1000
- 1s - loss: 788390.3121 - mean_squared_error: 788390.3121 - val_loss: 572093.5142 - val_mean_squared_error: 572093.5142
Epoch 94/1000
- 1s - loss: 784272.2464 - mean_squared_error: 784272.2464 - val_loss: 564077.7736 - val_mean_squared_error: 564077.7736
Epoch 95/1000
- 0s - loss: 781184.9639 - mean_squared_error: 781184.9639 - val_loss: 559705.1154 - val_mean_squared_error: 559705.1154
Epoch 96/1000
- 0s - loss: 779216.5293 - mean_squared_error: 779216.5293 - val_loss: 572421.8021 - val_mean_squared_error: 572421.8021
Epoch 97/1000
- 0s - loss: 777056.2196 - mean_squared_error: 777056.2196 - val_loss: 562629.6635 - val_mean_squared_error: 562629.6635
Epoch 98/1000
- 0s - loss: 773817.1616 - mean_squared_error: 773817.1616 - val_loss: 561004.9819 - val_mean_squared_error: 561004.9819
Epoch 99/1000
- 0s - loss: 771211.1602 - mean_squared_error: 771211.1602 - val_loss: 554090.3761 - val_mean_squared_error: 554090.3761
Epoch 100/1000
- 0s - loss: 767255.8413 - mean_squared_error: 767255.8413 - val_loss: 556355.2670 - val_mean_squared_error: 556355.2670
Epoch 101/1000
- 0s - loss: 765901.2514 - mean_squared_error: 765901.2514 - val_loss: 551462.6624 - val_mean_squared_error: 551462.6624
Epoch 102/1000
- 0s - loss: 764404.2335 - mean_squared_error: 764404.2335 - val_loss: 549381.3630 - val_mean_squared_error: 549381.3630
Epoch 103/1000
- 0s - loss: 761473.3068 - mean_squared_error: 761473.3068 - val_loss: 551158.3475 - val_mean_squared_error: 551158.3475
Epoch 104/1000
- 0s - loss: 758497.7380 - mean_squared_error: 758497.7380 - val_loss: 551972.1705 - val_mean_squared_error: 551972.1705
Epoch 105/1000
- 0s - loss: 755740.2717 - mean_squared_error: 755740.2717 - val_loss: 552988.2047 - val_mean_squared_error: 552988.2047
Epoch 106/1000
- 0s - loss: 751966.0399 - mean_squared_error: 751966.0399 - val_loss: 545469.4392 - val_mean_squared_error: 545469.4392
Epoch 107/1000
- 0s - loss: 749529.8615 - mean_squared_error: 749529.8615 - val_loss: 544913.2918 - val_mean_squared_error: 544913.2918
Epoch 108/1000
- 0s - loss: 746712.1812 - mean_squared_error: 746712.1812 - val_loss: 567939.2625 - val_mean_squared_error: 567939.2625
Epoch 109/1000
- 0s - loss: 746041.7362 - mean_squared_error: 746041.7362 - val_loss: 569642.5811 - val_mean_squared_error: 569642.5811
Epoch 110/1000
- 0s - loss: 743253.2273 - mean_squared_error: 743253.2273 - val_loss: 546741.9531 - val_mean_squared_error: 546741.9531
Epoch 111/1000
- 0s - loss: 738897.3570 - mean_squared_error: 738897.3570 - val_loss: 539759.7711 - val_mean_squared_error: 539759.7711
Epoch 112/1000
- 0s - loss: 737300.2927 - mean_squared_error: 737300.2927 - val_loss: 543091.0155 - val_mean_squared_error: 543091.0155
Epoch 113/1000
- 0s - loss: 736287.3635 - mean_squared_error: 736287.3635 - val_loss: 536867.4012 - val_mean_squared_error: 536867.4012
Epoch 114/1000
- 0s - loss: 732177.1100 - mean_squared_error: 732177.1100 - val_loss: 537107.3754 - val_mean_squared_error: 537107.3754
Epoch 115/1000
- 0s - loss: 729896.8594 - mean_squared_error: 729896.8594 - val_loss: 537009.4850 - val_mean_squared_error: 537009.4850
Epoch 116/1000
- 0s - loss: 726816.0095 - mean_squared_error: 726816.0095 - val_loss: 536977.3474 - val_mean_squared_error: 536977.3474
Epoch 117/1000
- 0s - loss: 725167.6049 - mean_squared_error: 725167.6049 - val_loss: 537228.8182 - val_mean_squared_error: 537228.8182
Epoch 118/1000
- 1s - loss: 724135.8915 - mean_squared_error: 724135.8915 - val_loss: 533379.5044 - val_mean_squared_error: 533379.5044
Epoch 119/1000
- 0s - loss: 722646.5176 - mean_squared_error: 722646.5176 - val_loss: 546342.7135 - val_mean_squared_error: 546342.7135
Epoch 120/1000
- 0s - loss: 718313.0591 - mean_squared_error: 718313.0591 - val_loss: 539371.5707 - val_mean_squared_error: 539371.5707
Epoch 121/1000
- 0s - loss: 715665.5330 - mean_squared_error: 715665.5330 - val_loss: 531296.1658 - val_mean_squared_error: 531296.1658
Epoch 122/1000
- 0s - loss: 713622.8886 - mean_squared_error: 713622.8886 - val_loss: 528986.8748 - val_mean_squared_error: 528986.8748
Epoch 123/1000
- 0s - loss: 710888.1242 - mean_squared_error: 710888.1242 - val_loss: 533666.9067 - val_mean_squared_error: 533666.9067
Epoch 124/1000
- 0s - loss: 708270.3770 - mean_squared_error: 708270.3770 - val_loss: 533409.4385 - val_mean_squared_error: 533409.4385
Epoch 125/1000
- 0s - loss: 707351.3229 - mean_squared_error: 707351.3229 - val_loss: 535185.1072 - val_mean_squared_error: 535185.1072
Epoch 126/1000
- 0s - loss: 704205.6693 - mean_squared_error: 704205.6693 - val_loss: 527617.6446 - val_mean_squared_error: 527617.6446
Epoch 127/1000
- 1s - loss: 702239.7262 - mean_squared_error: 702239.7262 - val_loss: 535940.2422 - val_mean_squared_error: 535940.2422
Epoch 128/1000
- 0s - loss: 698610.3730 - mean_squared_error: 698610.3730 - val_loss: 522318.7090 - val_mean_squared_error: 522318.7090
Epoch 129/1000
- 0s - loss: 696622.9261 - mean_squared_error: 696622.9261 - val_loss: 520506.7917 - val_mean_squared_error: 520506.7917
Epoch 130/1000
- 0s - loss: 694705.7903 - mean_squared_error: 694705.7903 - val_loss: 622523.0167 - val_mean_squared_error: 622523.0167
Epoch 131/1000
- 0s - loss: 693973.4791 - mean_squared_error: 693973.4791 - val_loss: 522661.4170 - val_mean_squared_error: 522661.4170
Epoch 132/1000
- 0s - loss: 691102.6542 - mean_squared_error: 691102.6542 - val_loss: 524003.7772 - val_mean_squared_error: 524003.7772
Epoch 133/1000
- 0s - loss: 687443.0615 - mean_squared_error: 687443.0615 - val_loss: 531624.0089 - val_mean_squared_error: 531624.0089
Epoch 134/1000
- 0s - loss: 684977.1058 - mean_squared_error: 684977.1058 - val_loss: 520965.2632 - val_mean_squared_error: 520965.2632
Epoch 135/1000
- 0s - loss: 683254.6634 - mean_squared_error: 683254.6634 - val_loss: 528877.9866 - val_mean_squared_error: 528877.9866
Epoch 136/1000
- 0s - loss: 681950.6925 - mean_squared_error: 681950.6925 - val_loss: 513907.0919 - val_mean_squared_error: 513907.0919
Epoch 137/1000
- 0s - loss: 677736.9771 - mean_squared_error: 677736.9771 - val_loss: 527688.9437 - val_mean_squared_error: 527688.9437
Epoch 138/1000
- 0s - loss: 675501.3018 - mean_squared_error: 675501.3018 - val_loss: 511479.7825 - val_mean_squared_error: 511479.7825
Epoch 139/1000
- 0s - loss: 672613.4058 - mean_squared_error: 672613.4058 - val_loss: 509692.0853 - val_mean_squared_error: 509692.0853
Epoch 140/1000
- 1s - loss: 672703.9846 - mean_squared_error: 672703.9846 - val_loss: 508695.8521 - val_mean_squared_error: 508695.8521
Epoch 141/1000
- 0s - loss: 670148.4179 - mean_squared_error: 670148.4179 - val_loss: 507927.2870 - val_mean_squared_error: 507927.2870
Epoch 142/1000
- 0s - loss: 666712.5280 - mean_squared_error: 666712.5280 - val_loss: 505714.2700 - val_mean_squared_error: 505714.2700
Epoch 143/1000
- 0s - loss: 664833.4980 - mean_squared_error: 664833.4980 - val_loss: 534800.6868 - val_mean_squared_error: 534800.6868
Epoch 144/1000
- 0s - loss: 662550.1644 - mean_squared_error: 662550.1644 - val_loss: 506006.4173 - val_mean_squared_error: 506006.4173
Epoch 145/1000
- 0s - loss: 660990.5031 - mean_squared_error: 660990.5031 - val_loss: 505433.1587 - val_mean_squared_error: 505433.1587
Epoch 146/1000
- 0s - loss: 656279.3769 - mean_squared_error: 656279.3769 - val_loss: 500965.6584 - val_mean_squared_error: 500965.6584
Epoch 147/1000
- 0s - loss: 654185.6563 - mean_squared_error: 654185.6563 - val_loss: 512835.3121 - val_mean_squared_error: 512835.3121
Epoch 148/1000
- 0s - loss: 653336.6825 - mean_squared_error: 653336.6825 - val_loss: 503334.4599 - val_mean_squared_error: 503334.4599
Epoch 149/1000
- 0s - loss: 651031.4121 - mean_squared_error: 651031.4121 - val_loss: 501340.8946 - val_mean_squared_error: 501340.8946
Epoch 150/1000
- 0s - loss: 646786.9940 - mean_squared_error: 646786.9940 - val_loss: 496265.3795 - val_mean_squared_error: 496265.3795
Epoch 151/1000
- 0s - loss: 645013.4190 - mean_squared_error: 645013.4190 - val_loss: 498710.8175 - val_mean_squared_error: 498710.8175
Epoch 152/1000
- 0s - loss: 641984.2047 - mean_squared_error: 641984.2047 - val_loss: 509091.8759 - val_mean_squared_error: 509091.8759
Epoch 153/1000
- 0s - loss: 641152.0855 - mean_squared_error: 641152.0855 - val_loss: 498405.3906 - val_mean_squared_error: 498405.3906
Epoch 154/1000
- 0s - loss: 638835.6091 - mean_squared_error: 638835.6091 - val_loss: 493089.1385 - val_mean_squared_error: 493089.1385
Epoch 155/1000
- 0s - loss: 637536.2370 - mean_squared_error: 637536.2370 - val_loss: 499518.0632 - val_mean_squared_error: 499518.0632
Epoch 156/1000
- 0s - loss: 634245.0132 - mean_squared_error: 634245.0132 - val_loss: 490638.1216 - val_mean_squared_error: 490638.1216
Epoch 157/1000
- 0s - loss: 629952.7305 - mean_squared_error: 629952.7305 - val_loss: 496781.1484 - val_mean_squared_error: 496781.1484
Epoch 158/1000
- 0s - loss: 628988.1684 - mean_squared_error: 628988.1684 - val_loss: 495213.6568 - val_mean_squared_error: 495213.6568
Epoch 159/1000
- 0s - loss: 626003.3835 - mean_squared_error: 626003.3835 - val_loss: 486876.1023 - val_mean_squared_error: 486876.1023
Epoch 160/1000
- 0s - loss: 624316.1100 - mean_squared_error: 624316.1100 - val_loss: 486944.3282 - val_mean_squared_error: 486944.3282
Epoch 161/1000
- 0s - loss: 622301.5767 - mean_squared_error: 622301.5767 - val_loss: 484524.2533 - val_mean_squared_error: 484524.2533
Epoch 162/1000
- 0s - loss: 620442.6938 - mean_squared_error: 620442.6938 - val_loss: 493503.7467 - val_mean_squared_error: 493503.7467
Epoch 163/1000
- 0s - loss: 618662.5856 - mean_squared_error: 618662.5856 - val_loss: 497317.4404 - val_mean_squared_error: 497317.4404
Epoch 164/1000
- 0s - loss: 615029.6842 - mean_squared_error: 615029.6842 - val_loss: 482182.9924 - val_mean_squared_error: 482182.9924
Epoch 165/1000
- 0s - loss: 614791.7386 - mean_squared_error: 614791.7386 - val_loss: 493360.0261 - val_mean_squared_error: 493360.0261
Epoch 166/1000
- 0s - loss: 611801.9160 - mean_squared_error: 611801.9160 - val_loss: 481002.4505 - val_mean_squared_error: 481002.4505
Epoch 167/1000
- 0s - loss: 608881.4007 - mean_squared_error: 608881.4007 - val_loss: 477675.2561 - val_mean_squared_error: 477675.2561
Epoch 168/1000
- 0s - loss: 609086.6959 - mean_squared_error: 609086.6959 - val_loss: 481496.7478 - val_mean_squared_error: 481496.7478
Epoch 169/1000
- 0s - loss: 608083.2661 - mean_squared_error: 608083.2661 - val_loss: 477560.9312 - val_mean_squared_error: 477560.9312
Epoch 170/1000
- 0s - loss: 604581.5461 - mean_squared_error: 604581.5461 - val_loss: 479526.0078 - val_mean_squared_error: 479526.0078
Epoch 171/1000
- 0s - loss: 602726.8338 - mean_squared_error: 602726.8338 - val_loss: 477001.6799 - val_mean_squared_error: 477001.6799
Epoch 172/1000
- 1s - loss: 600873.1875 - mean_squared_error: 600873.1875 - val_loss: 476275.0658 - val_mean_squared_error: 476275.0658
Epoch 173/1000
- 1s - loss: 599252.6168 - mean_squared_error: 599252.6168 - val_loss: 477493.4252 - val_mean_squared_error: 477493.4252
Epoch 174/1000
- 1s - loss: 596471.7464 - mean_squared_error: 596471.7464 - val_loss: 473096.2144 - val_mean_squared_error: 473096.2144
Epoch 175/1000
- 0s - loss: 593416.2096 - mean_squared_error: 593416.2096 - val_loss: 472148.0951 - val_mean_squared_error: 472148.0951
Epoch 176/1000
*** WARNING: skipped 89446 bytes of output ***
Epoch 829/1000
- 2s - loss: 345017.9668 - mean_squared_error: 345017.9668 - val_loss: 339550.3869 - val_mean_squared_error: 339550.3869
Epoch 830/1000
- 2s - loss: 345095.1452 - mean_squared_error: 345095.1452 - val_loss: 334828.6952 - val_mean_squared_error: 334828.6952
Epoch 831/1000
- 2s - loss: 345203.6046 - mean_squared_error: 345203.6046 - val_loss: 339119.3209 - val_mean_squared_error: 339119.3209
Epoch 832/1000
- 2s - loss: 344819.2877 - mean_squared_error: 344819.2877 - val_loss: 335065.9362 - val_mean_squared_error: 335065.9362
Epoch 833/1000
- 2s - loss: 346224.2386 - mean_squared_error: 346224.2386 - val_loss: 337110.6968 - val_mean_squared_error: 337110.6968
Epoch 834/1000
- 2s - loss: 344983.9361 - mean_squared_error: 344983.9361 - val_loss: 336426.7907 - val_mean_squared_error: 336426.7907
Epoch 835/1000
- 2s - loss: 345618.6019 - mean_squared_error: 345618.6019 - val_loss: 343576.4884 - val_mean_squared_error: 343576.4884
Epoch 836/1000
- 2s - loss: 344639.8262 - mean_squared_error: 344639.8262 - val_loss: 348924.4472 - val_mean_squared_error: 348924.4472
Epoch 837/1000
- 2s - loss: 344396.0252 - mean_squared_error: 344396.0252 - val_loss: 336985.3876 - val_mean_squared_error: 336985.3876
Epoch 838/1000
- 1s - loss: 345766.8460 - mean_squared_error: 345766.8460 - val_loss: 344635.9280 - val_mean_squared_error: 344635.9280
Epoch 839/1000
- 2s - loss: 345489.9858 - mean_squared_error: 345489.9858 - val_loss: 339979.3057 - val_mean_squared_error: 339979.3057
Epoch 840/1000
- 2s - loss: 345206.5084 - mean_squared_error: 345206.5084 - val_loss: 337119.9754 - val_mean_squared_error: 337119.9754
Epoch 841/1000
- 2s - loss: 343718.6248 - mean_squared_error: 343718.6248 - val_loss: 334405.6884 - val_mean_squared_error: 334405.6884
Epoch 842/1000
- 3s - loss: 344678.9692 - mean_squared_error: 344678.9692 - val_loss: 336524.3791 - val_mean_squared_error: 336524.3791
Epoch 843/1000
- 3s - loss: 343766.2976 - mean_squared_error: 343766.2976 - val_loss: 344220.5442 - val_mean_squared_error: 344220.5442
Epoch 844/1000
- 2s - loss: 343149.0991 - mean_squared_error: 343149.0991 - val_loss: 337221.7447 - val_mean_squared_error: 337221.7447
Epoch 845/1000
- 2s - loss: 345394.2195 - mean_squared_error: 345394.2195 - val_loss: 334977.3294 - val_mean_squared_error: 334977.3294
Epoch 846/1000
- 2s - loss: 343355.4561 - mean_squared_error: 343355.4561 - val_loss: 354574.3289 - val_mean_squared_error: 354574.3289
Epoch 847/1000
- 2s - loss: 343903.9672 - mean_squared_error: 343903.9672 - val_loss: 338111.1664 - val_mean_squared_error: 338111.1664
Epoch 848/1000
- 2s - loss: 344393.3413 - mean_squared_error: 344393.3413 - val_loss: 334853.7142 - val_mean_squared_error: 334853.7142
Epoch 849/1000
- 2s - loss: 342807.2594 - mean_squared_error: 342807.2594 - val_loss: 339990.1046 - val_mean_squared_error: 339990.1046
Epoch 850/1000
- 2s - loss: 343817.8121 - mean_squared_error: 343817.8121 - val_loss: 334133.9674 - val_mean_squared_error: 334133.9674
Epoch 851/1000
- 2s - loss: 342015.9391 - mean_squared_error: 342015.9391 - val_loss: 337267.7010 - val_mean_squared_error: 337267.7010
Epoch 852/1000
- 2s - loss: 343049.7382 - mean_squared_error: 343049.7382 - val_loss: 334921.4341 - val_mean_squared_error: 334921.4341
Epoch 853/1000
- 3s - loss: 341975.4870 - mean_squared_error: 341975.4870 - val_loss: 336409.5385 - val_mean_squared_error: 336409.5385
Epoch 854/1000
- 2s - loss: 343576.5908 - mean_squared_error: 343576.5908 - val_loss: 332839.1955 - val_mean_squared_error: 332839.1955
Epoch 855/1000
- 3s - loss: 341971.1491 - mean_squared_error: 341971.1491 - val_loss: 341118.1500 - val_mean_squared_error: 341118.1500
Epoch 856/1000
- 3s - loss: 341478.8825 - mean_squared_error: 341478.8825 - val_loss: 336649.9438 - val_mean_squared_error: 336649.9438
Epoch 857/1000
- 2s - loss: 342250.8677 - mean_squared_error: 342250.8677 - val_loss: 354445.1814 - val_mean_squared_error: 354445.1814
Epoch 858/1000
- 3s - loss: 342136.7264 - mean_squared_error: 342136.7264 - val_loss: 349826.4691 - val_mean_squared_error: 349826.4691
Epoch 859/1000
- 3s - loss: 342984.1812 - mean_squared_error: 342984.1812 - val_loss: 334444.6793 - val_mean_squared_error: 334444.6793
Epoch 860/1000
- 3s - loss: 341630.1121 - mean_squared_error: 341630.1121 - val_loss: 330739.8300 - val_mean_squared_error: 330739.8300
Epoch 861/1000
- 2s - loss: 341085.6488 - mean_squared_error: 341085.6488 - val_loss: 336881.8533 - val_mean_squared_error: 336881.8533
Epoch 862/1000
- 2s - loss: 341674.3046 - mean_squared_error: 341674.3046 - val_loss: 338649.9820 - val_mean_squared_error: 338649.9820
Epoch 863/1000
- 3s - loss: 341412.6696 - mean_squared_error: 341412.6696 - val_loss: 329679.5836 - val_mean_squared_error: 329679.5836
Epoch 864/1000
- 2s - loss: 342214.0651 - mean_squared_error: 342214.0651 - val_loss: 332068.0355 - val_mean_squared_error: 332068.0355
Epoch 865/1000
- 2s - loss: 340893.3589 - mean_squared_error: 340893.3589 - val_loss: 337983.0266 - val_mean_squared_error: 337983.0266
Epoch 866/1000
- 2s - loss: 340871.7239 - mean_squared_error: 340871.7239 - val_loss: 335902.1214 - val_mean_squared_error: 335902.1214
Epoch 867/1000
- 2s - loss: 341560.3707 - mean_squared_error: 341560.3707 - val_loss: 334970.9924 - val_mean_squared_error: 334970.9924
Epoch 868/1000
- 3s - loss: 340039.7690 - mean_squared_error: 340039.7690 - val_loss: 337636.2960 - val_mean_squared_error: 337636.2960
Epoch 869/1000
- 2s - loss: 339992.5361 - mean_squared_error: 339992.5361 - val_loss: 332152.1936 - val_mean_squared_error: 332152.1936
Epoch 870/1000
- 2s - loss: 340380.3068 - mean_squared_error: 340380.3068 - val_loss: 342874.4546 - val_mean_squared_error: 342874.4546
Epoch 871/1000
- 3s - loss: 340974.9624 - mean_squared_error: 340974.9624 - val_loss: 337238.6824 - val_mean_squared_error: 337238.6824
Epoch 872/1000
- 2s - loss: 341006.1794 - mean_squared_error: 341006.1794 - val_loss: 334961.9141 - val_mean_squared_error: 334961.9141
Epoch 873/1000
- 2s - loss: 340003.7552 - mean_squared_error: 340003.7552 - val_loss: 332399.2492 - val_mean_squared_error: 332399.2492
Epoch 874/1000
- 2s - loss: 339613.0568 - mean_squared_error: 339613.0568 - val_loss: 333346.4940 - val_mean_squared_error: 333346.4940
Epoch 875/1000
- 2s - loss: 339175.2896 - mean_squared_error: 339175.2896 - val_loss: 329275.6371 - val_mean_squared_error: 329275.6371
Epoch 876/1000
- 3s - loss: 340454.3724 - mean_squared_error: 340454.3724 - val_loss: 331445.7642 - val_mean_squared_error: 331445.7642
Epoch 877/1000
- 2s - loss: 339326.2713 - mean_squared_error: 339326.2713 - val_loss: 338601.9833 - val_mean_squared_error: 338601.9833
Epoch 878/1000
- 2s - loss: 339813.8287 - mean_squared_error: 339813.8287 - val_loss: 329877.1323 - val_mean_squared_error: 329877.1323
Epoch 879/1000
- 2s - loss: 338420.3591 - mean_squared_error: 338420.3591 - val_loss: 331026.2716 - val_mean_squared_error: 331026.2716
Epoch 880/1000
- 3s - loss: 339961.8071 - mean_squared_error: 339961.8071 - val_loss: 335541.0128 - val_mean_squared_error: 335541.0128
Epoch 881/1000
- 2s - loss: 338941.6191 - mean_squared_error: 338941.6191 - val_loss: 330347.3390 - val_mean_squared_error: 330347.3390
Epoch 882/1000
- 2s - loss: 339013.5767 - mean_squared_error: 339013.5767 - val_loss: 328106.2731 - val_mean_squared_error: 328106.2731
Epoch 883/1000
- 2s - loss: 337875.7955 - mean_squared_error: 337875.7955 - val_loss: 330178.5093 - val_mean_squared_error: 330178.5093
Epoch 884/1000
- 2s - loss: 339350.0852 - mean_squared_error: 339350.0852 - val_loss: 329480.1288 - val_mean_squared_error: 329480.1288
Epoch 885/1000
- 2s - loss: 338272.4309 - mean_squared_error: 338272.4309 - val_loss: 331816.4905 - val_mean_squared_error: 331816.4905
Epoch 886/1000
- 2s - loss: 337507.7292 - mean_squared_error: 337507.7292 - val_loss: 329787.4212 - val_mean_squared_error: 329787.4212
Epoch 887/1000
- 2s - loss: 338050.4211 - mean_squared_error: 338050.4211 - val_loss: 329916.1215 - val_mean_squared_error: 329916.1215
Epoch 888/1000
- 2s - loss: 338900.7663 - mean_squared_error: 338900.7663 - val_loss: 329637.2382 - val_mean_squared_error: 329637.2382
Epoch 889/1000
- 3s - loss: 338825.9054 - mean_squared_error: 338825.9054 - val_loss: 351477.4770 - val_mean_squared_error: 351477.4770
Epoch 890/1000
- 2s - loss: 338718.5214 - mean_squared_error: 338718.5214 - val_loss: 331109.1488 - val_mean_squared_error: 331109.1488
Epoch 891/1000
- 2s - loss: 336916.7545 - mean_squared_error: 336916.7545 - val_loss: 332089.4064 - val_mean_squared_error: 332089.4064
Epoch 892/1000
- 3s - loss: 337215.3815 - mean_squared_error: 337215.3815 - val_loss: 328642.7254 - val_mean_squared_error: 328642.7254
Epoch 893/1000
- 2s - loss: 336539.5405 - mean_squared_error: 336539.5405 - val_loss: 331523.8605 - val_mean_squared_error: 331523.8605
Epoch 894/1000
- 2s - loss: 336505.5508 - mean_squared_error: 336505.5508 - val_loss: 329752.4084 - val_mean_squared_error: 329752.4084
Epoch 895/1000
- 2s - loss: 338041.8457 - mean_squared_error: 338041.8457 - val_loss: 333375.2443 - val_mean_squared_error: 333375.2443
Epoch 896/1000
- 3s - loss: 336846.9650 - mean_squared_error: 336846.9650 - val_loss: 331127.2087 - val_mean_squared_error: 331127.2087
Epoch 897/1000
- 3s - loss: 337312.0117 - mean_squared_error: 337312.0117 - val_loss: 343776.1684 - val_mean_squared_error: 343776.1684
Epoch 898/1000
- 3s - loss: 336829.8278 - mean_squared_error: 336829.8278 - val_loss: 333697.3176 - val_mean_squared_error: 333697.3176
Epoch 899/1000
- 2s - loss: 337266.1198 - mean_squared_error: 337266.1198 - val_loss: 329812.2063 - val_mean_squared_error: 329812.2063
Epoch 900/1000
- 2s - loss: 336173.1526 - mean_squared_error: 336173.1526 - val_loss: 329260.7824 - val_mean_squared_error: 329260.7824
Epoch 901/1000
- 2s - loss: 337320.3509 - mean_squared_error: 337320.3509 - val_loss: 329677.7471 - val_mean_squared_error: 329677.7471
Epoch 902/1000
- 2s - loss: 336216.7482 - mean_squared_error: 336216.7482 - val_loss: 330786.0628 - val_mean_squared_error: 330786.0628
Epoch 903/1000
- 2s - loss: 335169.4466 - mean_squared_error: 335169.4466 - val_loss: 330023.5855 - val_mean_squared_error: 330023.5855
Epoch 904/1000
- 2s - loss: 334773.3664 - mean_squared_error: 334773.3664 - val_loss: 331348.3092 - val_mean_squared_error: 331348.3092
Epoch 905/1000
- 2s - loss: 337005.8331 - mean_squared_error: 337005.8331 - val_loss: 336718.0854 - val_mean_squared_error: 336718.0854
Epoch 906/1000
- 3s - loss: 336217.8212 - mean_squared_error: 336217.8212 - val_loss: 334061.6494 - val_mean_squared_error: 334061.6494
Epoch 907/1000
- 2s - loss: 337594.7403 - mean_squared_error: 337594.7403 - val_loss: 336332.3149 - val_mean_squared_error: 336332.3149
Epoch 908/1000
- 2s - loss: 336048.7730 - mean_squared_error: 336048.7730 - val_loss: 332418.5792 - val_mean_squared_error: 332418.5792
Epoch 909/1000
- 2s - loss: 335472.7371 - mean_squared_error: 335472.7371 - val_loss: 331683.5485 - val_mean_squared_error: 331683.5485
Epoch 910/1000
- 2s - loss: 335783.2895 - mean_squared_error: 335783.2895 - val_loss: 333249.9244 - val_mean_squared_error: 333249.9244
Epoch 911/1000
- 2s - loss: 336733.8351 - mean_squared_error: 336733.8351 - val_loss: 327430.1569 - val_mean_squared_error: 327430.1569
Epoch 912/1000
- 2s - loss: 335707.9263 - mean_squared_error: 335707.9263 - val_loss: 329743.7484 - val_mean_squared_error: 329743.7484
Epoch 913/1000
- 3s - loss: 336508.8904 - mean_squared_error: 336508.8904 - val_loss: 347242.2361 - val_mean_squared_error: 347242.2361
Epoch 914/1000
- 3s - loss: 338187.1960 - mean_squared_error: 338187.1960 - val_loss: 330245.9572 - val_mean_squared_error: 330245.9572
Epoch 915/1000
- 3s - loss: 335603.5673 - mean_squared_error: 335603.5673 - val_loss: 327345.1738 - val_mean_squared_error: 327345.1738
Epoch 916/1000
- 3s - loss: 336114.1620 - mean_squared_error: 336114.1620 - val_loss: 327426.3555 - val_mean_squared_error: 327426.3555
Epoch 917/1000
- 2s - loss: 334607.7871 - mean_squared_error: 334607.7871 - val_loss: 338000.0029 - val_mean_squared_error: 338000.0029
Epoch 918/1000
- 3s - loss: 336039.8853 - mean_squared_error: 336039.8853 - val_loss: 330842.1118 - val_mean_squared_error: 330842.1118
Epoch 919/1000
- 2s - loss: 334736.0575 - mean_squared_error: 334736.0575 - val_loss: 329386.8410 - val_mean_squared_error: 329386.8410
Epoch 920/1000
- 2s - loss: 334826.7755 - mean_squared_error: 334826.7755 - val_loss: 328047.4018 - val_mean_squared_error: 328047.4018
Epoch 921/1000
- 2s - loss: 335021.2916 - mean_squared_error: 335021.2916 - val_loss: 333844.6665 - val_mean_squared_error: 333844.6665
Epoch 922/1000
- 2s - loss: 333981.4889 - mean_squared_error: 333981.4889 - val_loss: 326704.3447 - val_mean_squared_error: 326704.3447
Epoch 923/1000
- 2s - loss: 334917.6133 - mean_squared_error: 334917.6133 - val_loss: 330501.8470 - val_mean_squared_error: 330501.8470
Epoch 924/1000
- 2s - loss: 334002.5516 - mean_squared_error: 334002.5516 - val_loss: 335391.1829 - val_mean_squared_error: 335391.1829
Epoch 925/1000
- 2s - loss: 334968.2855 - mean_squared_error: 334968.2855 - val_loss: 326628.8503 - val_mean_squared_error: 326628.8503
Epoch 926/1000
- 2s - loss: 332898.2530 - mean_squared_error: 332898.2530 - val_loss: 328397.5430 - val_mean_squared_error: 328397.5430
Epoch 927/1000
- 3s - loss: 334931.4404 - mean_squared_error: 334931.4404 - val_loss: 329709.7304 - val_mean_squared_error: 329709.7304
Epoch 928/1000
- 2s - loss: 332947.7994 - mean_squared_error: 332947.7994 - val_loss: 330066.7739 - val_mean_squared_error: 330066.7739
Epoch 929/1000
- 3s - loss: 335082.0854 - mean_squared_error: 335082.0854 - val_loss: 329052.2809 - val_mean_squared_error: 329052.2809
Epoch 930/1000
- 2s - loss: 334275.7794 - mean_squared_error: 334275.7794 - val_loss: 337873.2051 - val_mean_squared_error: 337873.2051
Epoch 931/1000
- 3s - loss: 334285.4401 - mean_squared_error: 334285.4401 - val_loss: 326295.5995 - val_mean_squared_error: 326295.5995
Epoch 932/1000
- 2s - loss: 333198.5096 - mean_squared_error: 333198.5096 - val_loss: 326851.9514 - val_mean_squared_error: 326851.9514
Epoch 933/1000
- 2s - loss: 332581.8137 - mean_squared_error: 332581.8137 - val_loss: 329371.6485 - val_mean_squared_error: 329371.6485
Epoch 934/1000
- 2s - loss: 335572.3163 - mean_squared_error: 335572.3163 - val_loss: 326771.3549 - val_mean_squared_error: 326771.3549
Epoch 935/1000
- 2s - loss: 333143.7913 - mean_squared_error: 333143.7913 - val_loss: 328063.1385 - val_mean_squared_error: 328063.1385
Epoch 936/1000
- 2s - loss: 333498.9271 - mean_squared_error: 333498.9271 - val_loss: 328116.8892 - val_mean_squared_error: 328116.8892
Epoch 937/1000
- 3s - loss: 334364.9447 - mean_squared_error: 334364.9447 - val_loss: 326289.5783 - val_mean_squared_error: 326289.5783
Epoch 938/1000
- 2s - loss: 333054.2822 - mean_squared_error: 333054.2822 - val_loss: 325446.7176 - val_mean_squared_error: 325446.7176
Epoch 939/1000
- 2s - loss: 332596.3337 - mean_squared_error: 332596.3337 - val_loss: 328647.7812 - val_mean_squared_error: 328647.7812
Epoch 940/1000
- 2s - loss: 333113.5899 - mean_squared_error: 333113.5899 - val_loss: 330894.5519 - val_mean_squared_error: 330894.5519
Epoch 941/1000
- 3s - loss: 333526.5784 - mean_squared_error: 333526.5784 - val_loss: 332395.0067 - val_mean_squared_error: 332395.0067
Epoch 942/1000
- 2s - loss: 332834.1839 - mean_squared_error: 332834.1839 - val_loss: 330302.9870 - val_mean_squared_error: 330302.9870
Epoch 943/1000
- 2s - loss: 332893.4333 - mean_squared_error: 332893.4333 - val_loss: 328957.5060 - val_mean_squared_error: 328957.5060
Epoch 944/1000
- 2s - loss: 331979.9354 - mean_squared_error: 331979.9354 - val_loss: 340494.6149 - val_mean_squared_error: 340494.6149
Epoch 945/1000
- 3s - loss: 332526.6156 - mean_squared_error: 332526.6156 - val_loss: 330565.7338 - val_mean_squared_error: 330565.7338
Epoch 946/1000
- 2s - loss: 334031.3728 - mean_squared_error: 334031.3728 - val_loss: 331275.0670 - val_mean_squared_error: 331275.0670
Epoch 947/1000
- 2s - loss: 331838.9002 - mean_squared_error: 331838.9002 - val_loss: 325802.9036 - val_mean_squared_error: 325802.9036
Epoch 948/1000
- 2s - loss: 331298.9476 - mean_squared_error: 331298.9476 - val_loss: 328504.1039 - val_mean_squared_error: 328504.1039
Epoch 949/1000
- 2s - loss: 334035.7380 - mean_squared_error: 334035.7380 - val_loss: 325919.3011 - val_mean_squared_error: 325919.3011
Epoch 950/1000
- 2s - loss: 331739.9385 - mean_squared_error: 331739.9385 - val_loss: 328578.6007 - val_mean_squared_error: 328578.6007
Epoch 951/1000
- 2s - loss: 333165.7279 - mean_squared_error: 333165.7279 - val_loss: 324289.7447 - val_mean_squared_error: 324289.7447
Epoch 952/1000
- 2s - loss: 333393.1627 - mean_squared_error: 333393.1627 - val_loss: 326171.1817 - val_mean_squared_error: 326171.1817
Epoch 953/1000
- 3s - loss: 331706.9216 - mean_squared_error: 331706.9216 - val_loss: 326917.4419 - val_mean_squared_error: 326917.4419
Epoch 954/1000
- 3s - loss: 331131.8147 - mean_squared_error: 331131.8147 - val_loss: 326759.7410 - val_mean_squared_error: 326759.7410
Epoch 955/1000
- 2s - loss: 331965.1028 - mean_squared_error: 331965.1028 - val_loss: 329673.9304 - val_mean_squared_error: 329673.9304
Epoch 956/1000
- 3s - loss: 333136.0035 - mean_squared_error: 333136.0035 - val_loss: 327953.4344 - val_mean_squared_error: 327953.4344
Epoch 957/1000
- 3s - loss: 331435.4059 - mean_squared_error: 331435.4059 - val_loss: 329612.4087 - val_mean_squared_error: 329612.4087
Epoch 958/1000
- 2s - loss: 331280.3102 - mean_squared_error: 331280.3102 - val_loss: 344775.1776 - val_mean_squared_error: 344775.1776
Epoch 959/1000
- 2s - loss: 330358.4627 - mean_squared_error: 330358.4627 - val_loss: 324788.5479 - val_mean_squared_error: 324788.5479
Epoch 960/1000
- 2s - loss: 331680.4408 - mean_squared_error: 331680.4408 - val_loss: 332945.2976 - val_mean_squared_error: 332945.2976
Epoch 961/1000
- 2s - loss: 331046.6944 - mean_squared_error: 331046.6944 - val_loss: 329599.2971 - val_mean_squared_error: 329599.2971
Epoch 962/1000
- 2s - loss: 330891.7869 - mean_squared_error: 330891.7869 - val_loss: 325052.2923 - val_mean_squared_error: 325052.2923
Epoch 963/1000
- 2s - loss: 331841.3119 - mean_squared_error: 331841.3119 - val_loss: 328403.7738 - val_mean_squared_error: 328403.7738
Epoch 964/1000
- 2s - loss: 331395.9604 - mean_squared_error: 331395.9604 - val_loss: 327710.5381 - val_mean_squared_error: 327710.5381
Epoch 965/1000
- 3s - loss: 330503.2513 - mean_squared_error: 330503.2513 - val_loss: 333109.0521 - val_mean_squared_error: 333109.0521
Epoch 966/1000
- 3s - loss: 332186.2043 - mean_squared_error: 332186.2043 - val_loss: 326552.9736 - val_mean_squared_error: 326552.9736
Epoch 967/1000
- 2s - loss: 330806.1350 - mean_squared_error: 330806.1350 - val_loss: 326002.8380 - val_mean_squared_error: 326002.8380
Epoch 968/1000
- 2s - loss: 330021.2170 - mean_squared_error: 330021.2170 - val_loss: 330944.9373 - val_mean_squared_error: 330944.9373
Epoch 969/1000
- 2s - loss: 330298.9462 - mean_squared_error: 330298.9462 - val_loss: 330188.9928 - val_mean_squared_error: 330188.9928
Epoch 970/1000
- 2s - loss: 331109.9404 - mean_squared_error: 331109.9404 - val_loss: 331563.9528 - val_mean_squared_error: 331563.9528
Epoch 971/1000
- 3s - loss: 329570.7982 - mean_squared_error: 329570.7982 - val_loss: 324951.1477 - val_mean_squared_error: 324951.1477
Epoch 972/1000
- 3s - loss: 329834.1170 - mean_squared_error: 329834.1170 - val_loss: 327184.0561 - val_mean_squared_error: 327184.0561
Epoch 973/1000
- 3s - loss: 330411.9112 - mean_squared_error: 330411.9112 - val_loss: 329343.6017 - val_mean_squared_error: 329343.6017
Epoch 974/1000
- 2s - loss: 331518.1610 - mean_squared_error: 331518.1610 - val_loss: 323144.2283 - val_mean_squared_error: 323144.2283
Epoch 975/1000
- 2s - loss: 329062.1325 - mean_squared_error: 329062.1325 - val_loss: 326323.0579 - val_mean_squared_error: 326323.0579
Epoch 976/1000
- 3s - loss: 330698.9198 - mean_squared_error: 330698.9198 - val_loss: 328326.8187 - val_mean_squared_error: 328326.8187
Epoch 977/1000
- 3s - loss: 330071.2349 - mean_squared_error: 330071.2349 - val_loss: 324667.7561 - val_mean_squared_error: 324667.7561
Epoch 978/1000
- 2s - loss: 331004.6893 - mean_squared_error: 331004.6893 - val_loss: 323948.6494 - val_mean_squared_error: 323948.6494
Epoch 979/1000
- 2s - loss: 332511.4398 - mean_squared_error: 332511.4398 - val_loss: 328892.2969 - val_mean_squared_error: 328892.2969
Epoch 980/1000
- 2s - loss: 330603.5983 - mean_squared_error: 330603.5983 - val_loss: 325858.7483 - val_mean_squared_error: 325858.7483
Epoch 981/1000
- 3s - loss: 330158.9787 - mean_squared_error: 330158.9787 - val_loss: 325834.5056 - val_mean_squared_error: 325834.5056
Epoch 982/1000
- 2s - loss: 330353.8880 - mean_squared_error: 330353.8880 - val_loss: 325544.3455 - val_mean_squared_error: 325544.3455
Epoch 983/1000
- 3s - loss: 329292.4320 - mean_squared_error: 329292.4320 - val_loss: 325120.8610 - val_mean_squared_error: 325120.8610
Epoch 984/1000
- 3s - loss: 329400.8035 - mean_squared_error: 329400.8035 - val_loss: 324350.4380 - val_mean_squared_error: 324350.4380
Epoch 985/1000
- 2s - loss: 330789.6305 - mean_squared_error: 330789.6305 - val_loss: 327118.8064 - val_mean_squared_error: 327118.8064
Epoch 986/1000
- 2s - loss: 329059.9164 - mean_squared_error: 329059.9164 - val_loss: 328578.1070 - val_mean_squared_error: 328578.1070
Epoch 987/1000
- 2s - loss: 329473.6236 - mean_squared_error: 329473.6236 - val_loss: 324709.3233 - val_mean_squared_error: 324709.3233
Epoch 988/1000
- 2s - loss: 329018.8897 - mean_squared_error: 329018.8897 - val_loss: 325750.0715 - val_mean_squared_error: 325750.0715
Epoch 989/1000
- 2s - loss: 329210.6551 - mean_squared_error: 329210.6551 - val_loss: 324165.1183 - val_mean_squared_error: 324165.1183
Epoch 990/1000
- 2s - loss: 328681.8209 - mean_squared_error: 328681.8209 - val_loss: 324837.2337 - val_mean_squared_error: 324837.2337
Epoch 991/1000
- 2s - loss: 332326.2836 - mean_squared_error: 332326.2836 - val_loss: 324704.5920 - val_mean_squared_error: 324704.5920
Epoch 992/1000
- 2s - loss: 329117.0329 - mean_squared_error: 329117.0329 - val_loss: 326161.4024 - val_mean_squared_error: 326161.4024
Epoch 993/1000
- 3s - loss: 329799.5372 - mean_squared_error: 329799.5372 - val_loss: 328298.2622 - val_mean_squared_error: 328298.2622
Epoch 994/1000
- 2s - loss: 329550.7582 - mean_squared_error: 329550.7582 - val_loss: 323986.6425 - val_mean_squared_error: 323986.6425
Epoch 995/1000
- 2s - loss: 328281.8657 - mean_squared_error: 328281.8657 - val_loss: 325990.0735 - val_mean_squared_error: 325990.0735
Epoch 996/1000
- 2s - loss: 328922.3964 - mean_squared_error: 328922.3964 - val_loss: 324806.7343 - val_mean_squared_error: 324806.7343
Epoch 997/1000
- 2s - loss: 328507.0786 - mean_squared_error: 328507.0786 - val_loss: 346090.4408 - val_mean_squared_error: 346090.4408
Epoch 998/1000
- 2s - loss: 329783.5376 - mean_squared_error: 329783.5376 - val_loss: 324142.9919 - val_mean_squared_error: 324142.9919
Epoch 999/1000
- 2s - loss: 328829.8128 - mean_squared_error: 328829.8128 - val_loss: 326034.4199 - val_mean_squared_error: 326034.4199
Epoch 1000/1000
- 2s - loss: 328443.1473 - mean_squared_error: 328443.1473 - val_loss: 327467.0317 - val_mean_squared_error: 327467.0317
32/13485 [..............................] - ETA: 1s
704/13485 [>.............................] - ETA: 1s
1152/13485 [=>............................] - ETA: 1s
1792/13485 [==>...........................] - ETA: 1s
2496/13485 [====>.........................] - ETA: 0s
3104/13485 [=====>........................] - ETA: 0s
3520/13485 [======>.......................] - ETA: 0s
3936/13485 [=======>......................] - ETA: 0s
4576/13485 [=========>....................] - ETA: 0s
5056/13485 [==========>...................] - ETA: 0s
5472/13485 [===========>..................] - ETA: 0s
5824/13485 [===========>..................] - ETA: 0s
6336/13485 [=============>................] - ETA: 0s
6848/13485 [==============>...............] - ETA: 0s
7456/13485 [===============>..............] - ETA: 0s
8224/13485 [=================>............] - ETA: 0s
8992/13485 [===================>..........] - ETA: 0s
9728/13485 [====================>.........] - ETA: 0s
10208/13485 [=====================>........] - ETA: 0s
10912/13485 [=======================>......] - ETA: 0s
11424/13485 [========================>.....] - ETA: 0s
11904/13485 [=========================>....] - ETA: 0s
12384/13485 [==========================>...] - ETA: 0s
12960/13485 [===========================>..] - ETA: 0s
13485/13485 [==============================] - 1s 94us/step
root mean_squared_error: 587.802047
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
TensorFlow
... is a general math framework
TensorFlow is designed to accommodate...
- Easy operations on tensors (n-dimensional arrays)
- Mappings to performant low-level implementations, including native CPU and GPU
- Optimization via gradient descent variants
- Including high-performance differentiation
Low-level math primitives called "Ops"
From these primitives, linear algebra and other higher-level constructs are formed.
Going up one more level common neural-net components have been built and included.
At an even higher level of abstraction, various libraries have been created that simplify building and wiring common network patterns. Over the last 2 years, we've seen 3-5 such libraries.
We will focus later on one, Keras, which has now been adopted as the "official" high-level wrapper for TensorFlow.
We'll get familiar with TensorFlow so that it is not a "magic black box"
But for most of our work, it will be more productive to work with the higher-level wrappers. At the end of this notebook, we'll make the connection between the Keras API we've used and the TensorFlow code underneath.
import tensorflow as tf
x = tf.constant(100, name='x')
y = tf.Variable(x + 50, name='y')
print(y)
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
<tf.Variable 'y:0' shape=() dtype=int32_ref>
There's a bit of "ceremony" there...
... and ... where's the actual output?
For performance reasons, TensorFlow separates the design of the computation from the actual execution.
TensorFlow programs describe a computation graph -- an abstract DAG of data flow -- that can then be analyzed, optimized, and implemented on a variety of hardware, as well as potentially scheduled across a cluster of separate machines.
Like many query engines and compute graph engines, evaluation is lazy ... so we don't get "real numbers" until we force TensorFlow to run the calculation:
init_node = tf.global_variables_initializer()
with tf.Session() as session:
session.run(init_node)
print(session.run(y))
150
TensorFlow integrates tightly with NumPy
and we typically use NumPy to create and manage the tensors (vectors, matrices, etc.) that will "flow" through our graph
New to NumPy? Grab a cheat sheet: https://s3.amazonaws.com/assets.datacamp.com/blogassets/NumpyPythonCheatSheet.pdf
import numpy as np
data = np.random.normal(loc=10.0, scale=2.0, size=[3,3]) # mean 10, std dev 2
print(data)
[[11.39104009 10.74646715 9.97434901]
[10.85377817 10.18047268 8.54517234]
[ 7.50991424 8.92290223 7.32137675]]
# all nodes get added to default graph (unless we specify otherwise)
# we can reset the default graph -- so it's not cluttered up:
tf.reset_default_graph()
x = tf.constant(data, name='x')
y = tf.Variable(x * 10, name='y')
init_node = tf.global_variables_initializer()
with tf.Session() as session:
session.run(init_node)
print(session.run(y))
[[113.91040088 107.46467153 99.74349013]
[108.53778169 101.80472682 85.45172335]
[ 75.09914241 89.22902232 73.21376755]]
We will often iterate on a calculation ...
Calling session.run runs just one step, so we can iterate using Python as a control:
with tf.Session() as session:
for i in range(3):
x = x + 1
print(session.run(x))
print("----------------------------------------------")
[[12.39104009 11.74646715 10.97434901]
[11.85377817 11.18047268 9.54517234]
[ 8.50991424 9.92290223 8.32137675]]
----------------------------------------------
[[13.39104009 12.74646715 11.97434901]
[12.85377817 12.18047268 10.54517234]
[ 9.50991424 10.92290223 9.32137675]]
----------------------------------------------
[[14.39104009 13.74646715 12.97434901]
[13.85377817 13.18047268 11.54517234]
[10.50991424 11.92290223 10.32137675]]
----------------------------------------------
Optimizers
TF includes a set of built-in algorithm implementations (though you could certainly write them yourself) for performing optimization.
These are oriented around gradient-descent methods, with a set of handy extension flavors to make things converge faster.
Using TF optimizer to solve problems
We can use the optimizers to solve anything (not just neural networks) so let's start with a simple equation.
We supply a bunch of data points, that represent inputs. We will generate them based on a known, simple equation (y will always be 2*x + 6) but we won't tell TF that. Instead, we will give TF a function structure ... linear with 2 parameters, and let TF try to figure out the parameters by minimizing an error function.
What is the error function?
The "real" error is the absolute value of the difference between TF's current approximation and our ground-truth y value.
But absolute value is not a friendly function to work with there, so instead we'll square it. That gets us a nice, smooth function that TF can work with, and it's just as good:
np.random.rand()
x = tf.placeholder("float")
y = tf.placeholder("float")
m = tf.Variable([1.0], name="m-slope-coefficient") # initial values ... for now they don't matter much
b = tf.Variable([1.0], name="b-intercept")
y_model = tf.multiply(x, m) + b
error = tf.square(y - y_model)
train_op = tf.train.GradientDescentOptimizer(0.01).minimize(error)
model = tf.global_variables_initializer()
with tf.Session() as session:
session.run(model)
for i in range(10):
x_value = np.random.rand()
y_value = x_value * 2 + 6 # we know these params, but we're making TF learn them
session.run(train_op, feed_dict={x: x_value, y: y_value})
out = session.run([m, b])
print(out)
print("Model: {r:.3f}x + {s:.3f}".format(r=out[0][0], s=out[1][0]))
[array([1.6890278], dtype=float32), array([1.9976655], dtype=float32)]
Model: 1.689x + 1.998
That's pretty terrible :)
Try two experiments. Change the number of iterations the optimizer runs, and -- independently -- try changing the learning rate (that's the number we passed to GradientDescentOptimizer)
See what happens with different values.
These are scalars. Where do the tensors come in?
Using matrices allows us to represent (and, with the right hardware, compute) the data-weight dot products for lots of data vectors (a mini batch) and lots of weight vectors (neurons) at the same time.
Tensors are useful because some of our data "vectors" are really multidimensional -- for example, with a color image we may want to preserve height, width, and color planes. We can hold multiple color images, with their shapes, in a 4-D (or 4 "axis") tensor.
Let's also make the connection from Keras down to Tensorflow.
We used a Keras class called Dense, which represents a "fully-connected" layer of -- in this case -- linear perceptrons. Let's look at the source code to that, just to see that there's no mystery.
https://github.com/fchollet/keras/blob/master/keras/layers/core.py
It calls down to the "back end" by calling output = K.dot(inputs, self.kernel) where kernel means this layer's weights.
K represents the pluggable backend wrapper. You can trace K.dot on Tensorflow by looking at
https://github.com/fchollet/keras/blob/master/keras/backend/tensorflow_backend.py
Look for def dot(x, y): and look right toward the end of the method. The math is done by calling tf.matmul(x, y)
What else helps Tensorflow (and other frameworks) run fast?
- A fast, simple mechanism for calculating all of the partial derivatives we need, called reverse-mode autodifferentiation
- Implementations of low-level operations in optimized CPU code (e.g., C++, MKL) and GPU code (CUDA/CuDNN/HLSL)
- Support for distributed parallel training, although parallelizing deep learning is non-trivial ... not automagic like with, e.g., Apache Spark
That is the essence of TensorFlow!
There are three principal directions to explore further:
-
Working with tensors instead of scalars: this is not intellectually difficult, but takes some practice to wrangle the shaping and re-shaping of tensors. If you get the shape of a tensor wrong, your script will blow up. Just takes practice.
-
Building more complex models. You can write these yourself using lower level "Ops" -- like matrix multiply -- or using higher level classes like
tf.layers.denseUse the source, Luke! -
Operations and integration ecosystem: as TensorFlow has matured, it is easier to integrate additional tools and solve the peripheral problems:
- TensorBoard for visualizing training
- tfdbg command-line debugger
- Distributed TensorFlow for clustered training
- GPU integration
- Feeding large datasets from external files
- Tensorflow Serving for serving models (i.e., using an existing model to predict on new incoming data)
Distirbuted Training for DL
- https://docs.azuredatabricks.net/applications/deep-learning/distributed-training/horovod-runner.html
- https://docs.azuredatabricks.net/applications/deep-learning/distributed-training/mnist-tensorflow-keras.html
- https://software.intel.com/en-us/articles/bigdl-distributed-deep-learning-on-apache-spark
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
We can also implement the model with mini-batches -- this will let us see matrix ops in action:
(N.b., feeddict is intended for small data / experimentation. For more info on ingesting data at scale, see https://www.tensorflow.org/apiguides/python/reading_data)
# we know these params, but we're making TF learn them
REAL_SLOPE_X1 = 2 # slope along axis 1 (x-axis)
REAL_SLOPE_X2 = 3 # slope along axis 2 (y-axis)
REAL_INTERCEPT = 5 # intercept along axis 3 (z-axis), think of (x,y,z) axes in the usual way
import numpy as np
# GENERATE a batch of true data, with a little Gaussian noise added
def make_mini_batch(size=10):
X = np.random.rand(size, 2) #
Y = np.matmul(X, [REAL_SLOPE_X1, REAL_SLOPE_X2]) + REAL_INTERCEPT + 0.2 * np.random.randn(size)
return X.reshape(size,2), Y.reshape(size,1)
To digest what's going on inside the function above, let's take it step by step.
Xex = np.random.rand(10, 2) # Xex is simulating PRNGs from independent Uniform [0,1] RVs
Xex # visualize these as 10 orddered pairs of points in the x-y plane that makes up our x-axis and y-axis (or x1 and x2 axes)
Yex = np.matmul(Xex, [REAL_SLOPE_X1, REAL_SLOPE_X2]) #+ REAL_INTERCEPT #+ 0.2 * np.random.randn(10)
Yex
The first entry in Yex is obtained as follows (change the numbers in the produc below if you reevaluated the cells above) and geometrically it is the location in z-axis of the plane with slopes given by REALSLOPEX1 in the x-axis and REALSLOPEX2 in the y-aixs with intercept 0 at the point in the x-y or x1-x2 plane given by (0.68729439, 0.58462379).
0.21757443*REAL_SLOPE_X1 + 0.01815727*REAL_SLOPE_X2
The next steps are adding an intercept term to translate the plane in the z-axis and then a scaled (the multiplication by 0.2 here) gaussian noise from independetly drawn pseudo-random samples from the standard normal or Normal(0,1) random variable via np.random.randn(size).
Yex = np.matmul(Xex, [REAL_SLOPE_X1, REAL_SLOPE_X2]) + REAL_INTERCEPT # + 0.2 * np.random.randn(10)
Yex
Yex = np.matmul(Xex, [REAL_SLOPE_X1, REAL_SLOPE_X2]) + REAL_INTERCEPT + 0.2 * np.random.randn(10)
Yex # note how each entry in Yex is jiggled independently a bit by 0.2 * np.random.randn()
Thus we can now fully appreciate what is going on in make_mini_batch. This is meant to substitute for pulling random sub-samples of batches of the real data during stochastic gradient descent.
make_mini_batch() # our mini-batch of Xx and Ys
import tensorflow as tf
batch = 10 # size of batch
tf.reset_default_graph() # this is important to do before you do something new in TF
# we will work with single floating point precision and this is specified in the tf.float32 type argument to each tf object/method
x = tf.placeholder(tf.float32, shape=(batch, 2)) # placeholder node for the pairs of x variables (predictors) in batches of size batch
x_aug = tf.concat( (x, tf.ones((batch, 1))), 1 ) # x_aug is a concatenation of a vector of 1`s along the first dimension
y = tf.placeholder(tf.float32, shape=(batch, 1)) # placeholder node for the univariate response y with batch many rows and 1 column
model_params = tf.get_variable("model_params", [3,1]) # these are the x1 slope, x2 slope and the intercept (3 rows and 1 column)
y_model = tf.matmul(x_aug, model_params) # our two-factor regression model is defined by this matrix multiplication
# note that the noise is formally part of the model and what we are actually modeling is the mean response...
error = tf.reduce_sum(tf.square(y - y_model))/batch # this is mean square error where the sum is computed by a reduce call on addition
train_op = tf.train.GradientDescentOptimizer(0.02).minimize(error) # learning rate is set to 0.02
init = tf.global_variables_initializer() # our way into running the TF session
errors = [] # list to track errors over iterations
with tf.Session() as session:
session.run(init)
for i in range(1000):
x_data, y_data = make_mini_batch(batch) # simulate the mini-batch of data x1,x2 and response y with noise
_, error_val = session.run([train_op, error], feed_dict={x: x_data, y: y_data})
errors.append(error_val)
out = session.run(model_params)
print(out)
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
[[2.0491152]
[3.0319374]
[4.961138 ]]
REAL_SLOPE_X1, REAL_SLOPE_X2, REAL_INTERCEPT # compare with rue parameter values - it's not too far from the estimates
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
fig.set_size_inches((4,3))
plt.plot(errors)
display(fig)
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
As a baseline, let's start a lab running with what we already know.
We'll take our deep feed-forward multilayer perceptron network, with ReLU activations and reasonable initializations, and apply it to learning the MNIST digits.
The main part of the code looks like the following (full code you can run is in the next cell):
# imports, setup, load data sets
model = Sequential()
model.add(Dense(20, input_dim=784, kernel_initializer='normal', activation='relu'))
model.add(Dense(15, kernel_initializer='normal', activation='relu'))
model.add(Dense(10, kernel_initializer='normal', activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['categorical_accuracy'])
categorical_labels = to_categorical(y_train, num_classes=10)
history = model.fit(X_train, categorical_labels, epochs=100, batch_size=100)
# print metrics, plot errors
Note the changes, which are largely about building a classifier instead of a regression model: * Output layer has one neuron per category, with softmax activation * Loss function is cross-entropy loss * Accuracy metric is categorical accuracy
Let's hold pointers into wikipedia for these new concepts.
The following is from: https://www.quora.com/How-does-Keras-calculate-accuracy.
Categorical accuracy:
def categorical_accuracy(y_true, y_pred):
return K.cast(K.equal(K.argmax(y_true, axis=-1),
K.argmax(y_pred, axis=-1)),
K.floatx())
K.argmax(y_true)takes the highest value to be the prediction and matches against the comparative set.
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import to_categorical
import sklearn.datasets
import datetime
import matplotlib.pyplot as plt
import numpy as np
train_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-train.txt"
test_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-test.txt"
X_train, y_train = sklearn.datasets.load_svmlight_file(train_libsvm, n_features=784)
X_train = X_train.toarray()
X_test, y_test = sklearn.datasets.load_svmlight_file(test_libsvm, n_features=784)
X_test = X_test.toarray()
model = Sequential()
model.add(Dense(20, input_dim=784, kernel_initializer='normal', activation='relu'))
model.add(Dense(15, kernel_initializer='normal', activation='relu'))
model.add(Dense(10, kernel_initializer='normal', activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['categorical_accuracy'])
categorical_labels = to_categorical(y_train, num_classes=10)
start = datetime.datetime.today()
history = model.fit(X_train, categorical_labels, epochs=40, batch_size=100, validation_split=0.1, verbose=2)
scores = model.evaluate(X_test, to_categorical(y_test, num_classes=10))
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
print ("Start: " + str(start))
end = datetime.datetime.today()
print ("End: " + str(end))
print ("Elapse: " + str(end-start))
Using TensorFlow backend.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 54000 samples, validate on 6000 samples
Epoch 1/40
- 2s - loss: 0.5150 - categorical_accuracy: 0.8445 - val_loss: 0.2426 - val_categorical_accuracy: 0.9282
Epoch 2/40
- 2s - loss: 0.2352 - categorical_accuracy: 0.9317 - val_loss: 0.1763 - val_categorical_accuracy: 0.9487
Epoch 3/40
- 2s - loss: 0.1860 - categorical_accuracy: 0.9454 - val_loss: 0.1526 - val_categorical_accuracy: 0.9605
Epoch 4/40
- 1s - loss: 0.1602 - categorical_accuracy: 0.9527 - val_loss: 0.1600 - val_categorical_accuracy: 0.9573
Epoch 5/40
- 2s - loss: 0.1421 - categorical_accuracy: 0.9575 - val_loss: 0.1464 - val_categorical_accuracy: 0.9590
Epoch 6/40
- 1s - loss: 0.1277 - categorical_accuracy: 0.9611 - val_loss: 0.1626 - val_categorical_accuracy: 0.9568
Epoch 7/40
- 1s - loss: 0.1216 - categorical_accuracy: 0.9610 - val_loss: 0.1263 - val_categorical_accuracy: 0.9665
Epoch 8/40
- 2s - loss: 0.1136 - categorical_accuracy: 0.9656 - val_loss: 0.1392 - val_categorical_accuracy: 0.9627
Epoch 9/40
- 2s - loss: 0.1110 - categorical_accuracy: 0.9659 - val_loss: 0.1306 - val_categorical_accuracy: 0.9632
Epoch 10/40
- 1s - loss: 0.1056 - categorical_accuracy: 0.9678 - val_loss: 0.1298 - val_categorical_accuracy: 0.9643
Epoch 11/40
- 1s - loss: 0.1010 - categorical_accuracy: 0.9685 - val_loss: 0.1523 - val_categorical_accuracy: 0.9583
Epoch 12/40
- 2s - loss: 0.1003 - categorical_accuracy: 0.9692 - val_loss: 0.1540 - val_categorical_accuracy: 0.9583
Epoch 13/40
- 1s - loss: 0.0929 - categorical_accuracy: 0.9713 - val_loss: 0.1348 - val_categorical_accuracy: 0.9647
Epoch 14/40
- 1s - loss: 0.0898 - categorical_accuracy: 0.9716 - val_loss: 0.1476 - val_categorical_accuracy: 0.9628
Epoch 15/40
- 1s - loss: 0.0885 - categorical_accuracy: 0.9722 - val_loss: 0.1465 - val_categorical_accuracy: 0.9633
Epoch 16/40
- 2s - loss: 0.0840 - categorical_accuracy: 0.9736 - val_loss: 0.1584 - val_categorical_accuracy: 0.9623
Epoch 17/40
- 2s - loss: 0.0844 - categorical_accuracy: 0.9730 - val_loss: 0.1530 - val_categorical_accuracy: 0.9598
Epoch 18/40
- 2s - loss: 0.0828 - categorical_accuracy: 0.9739 - val_loss: 0.1395 - val_categorical_accuracy: 0.9662
Epoch 19/40
- 2s - loss: 0.0782 - categorical_accuracy: 0.9755 - val_loss: 0.1640 - val_categorical_accuracy: 0.9623
Epoch 20/40
- 1s - loss: 0.0770 - categorical_accuracy: 0.9760 - val_loss: 0.1638 - val_categorical_accuracy: 0.9568
Epoch 21/40
- 1s - loss: 0.0754 - categorical_accuracy: 0.9763 - val_loss: 0.1773 - val_categorical_accuracy: 0.9608
Epoch 22/40
- 2s - loss: 0.0742 - categorical_accuracy: 0.9769 - val_loss: 0.1767 - val_categorical_accuracy: 0.9603
Epoch 23/40
- 2s - loss: 0.0762 - categorical_accuracy: 0.9762 - val_loss: 0.1623 - val_categorical_accuracy: 0.9597
Epoch 24/40
- 1s - loss: 0.0724 - categorical_accuracy: 0.9772 - val_loss: 0.1647 - val_categorical_accuracy: 0.9635
Epoch 25/40
- 1s - loss: 0.0701 - categorical_accuracy: 0.9781 - val_loss: 0.1705 - val_categorical_accuracy: 0.9623
Epoch 26/40
- 2s - loss: 0.0702 - categorical_accuracy: 0.9777 - val_loss: 0.1673 - val_categorical_accuracy: 0.9658
Epoch 27/40
- 2s - loss: 0.0682 - categorical_accuracy: 0.9788 - val_loss: 0.1841 - val_categorical_accuracy: 0.9607
Epoch 28/40
- 2s - loss: 0.0684 - categorical_accuracy: 0.9790 - val_loss: 0.1738 - val_categorical_accuracy: 0.9623
Epoch 29/40
- 2s - loss: 0.0670 - categorical_accuracy: 0.9786 - val_loss: 0.1880 - val_categorical_accuracy: 0.9610
Epoch 30/40
- 2s - loss: 0.0650 - categorical_accuracy: 0.9790 - val_loss: 0.1765 - val_categorical_accuracy: 0.9650
Epoch 31/40
- 2s - loss: 0.0639 - categorical_accuracy: 0.9793 - val_loss: 0.1774 - val_categorical_accuracy: 0.9602
Epoch 32/40
- 2s - loss: 0.0660 - categorical_accuracy: 0.9791 - val_loss: 0.1885 - val_categorical_accuracy: 0.9622
Epoch 33/40
- 1s - loss: 0.0636 - categorical_accuracy: 0.9795 - val_loss: 0.1928 - val_categorical_accuracy: 0.9595
Epoch 34/40
- 1s - loss: 0.0597 - categorical_accuracy: 0.9805 - val_loss: 0.1948 - val_categorical_accuracy: 0.9593
Epoch 35/40
- 2s - loss: 0.0631 - categorical_accuracy: 0.9797 - val_loss: 0.2019 - val_categorical_accuracy: 0.9563
Epoch 36/40
- 2s - loss: 0.0600 - categorical_accuracy: 0.9812 - val_loss: 0.1852 - val_categorical_accuracy: 0.9595
Epoch 37/40
- 2s - loss: 0.0597 - categorical_accuracy: 0.9812 - val_loss: 0.1794 - val_categorical_accuracy: 0.9637
Epoch 38/40
- 2s - loss: 0.0588 - categorical_accuracy: 0.9812 - val_loss: 0.1933 - val_categorical_accuracy: 0.9625
Epoch 39/40
- 2s - loss: 0.0629 - categorical_accuracy: 0.9805 - val_loss: 0.2177 - val_categorical_accuracy: 0.9582
Epoch 40/40
- 2s - loss: 0.0559 - categorical_accuracy: 0.9828 - val_loss: 0.1875 - val_categorical_accuracy: 0.9642
32/10000 [..............................] - ETA: 0s
1568/10000 [===>..........................] - ETA: 0s
3072/10000 [========>.....................] - ETA: 0s
4672/10000 [=============>................] - ETA: 0s
6496/10000 [==================>...........] - ETA: 0s
8192/10000 [=======================>......] - ETA: 0s
10000/10000 [==============================] - 0s 30us/step
loss: 0.227984
categorical_accuracy: 0.954900
Start: 2021-02-10 10:20:06.310772
End: 2021-02-10 10:21:10.141213
Elapse: 0:01:03.830441
after about a minute we have:
...
Epoch 40/40
1s - loss: 0.0610 - categorical_accuracy: 0.9809 - val_loss: 0.1918 - val_categorical_accuracy: 0.9583
...
loss: 0.216120
categorical_accuracy: 0.955000
Start: 2017-12-06 07:35:33.948102
End: 2017-12-06 07:36:27.046130
Elapse: 0:00:53.098028
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
fig.set_size_inches((5,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
display(fig)
What are the big takeaways from this experiment?
- We get pretty impressive "apparent error" accuracy right from the start! A small network gets us to training accuracy 97% by epoch 20
- The model appears to continue to learn if we let it run, although it does slow down and oscillate a bit.
- Our test accuracy is about 95% after 5 epochs and never gets better ... it gets worse!
- Therefore, we are overfitting very quickly... most of the "training" turns out to be a waste.
- For what it's worth, we get 95% accuracy without much work.
This is not terrible compared to other, non-neural-network approaches to the problem. After all, we could probably tweak this a bit and do even better.
But we talked about using deep learning to solve "95%" problems or "98%" problems ... where one error in 20, or 50 simply won't work. If we can get to "multiple nines" of accuracy, then we can do things like automate mail sorting and translation, create cars that react properly (all the time) to street signs, and control systems for robots or drones that function autonomously.
Try two more experiments (try them separately): 1. Add a third, hidden layer. 2. Increase the size of the hidden layers.
Adding another layer slows things down a little (why?) but doesn't seem to make a difference in accuracy.
Adding a lot more neurons into the first topology slows things down significantly -- 10x as many neurons, and only a marginal increase in accuracy. Notice also (in the plot) that the learning clearly degrades after epoch 50 or so.
... We need a new approach!
... let's think about this:
What is layer 2 learning from layer 1? Combinations of pixels
Combinations of pixels contain information but...
There are a lot of them (combinations) and they are "fragile"
In fact, in our last experiment, we basically built a model that memorizes a bunch of "magic" pixel combinations.
What might be a better way to build features?
- When humans perform this task, we look not at arbitrary pixel combinations, but certain geometric patterns -- lines, curves, loops.
- These features are made up of combinations of pixels, but they are far from arbitrary
- We identify these features regardless of translation, rotation, etc.
Is there a way to get the network to do the same thing?
I.e., in layer one, identify pixels. Then in layer 2+, identify abstractions over pixels that are translation-invariant 2-D shapes?
We could look at where a "filter" that represents one of these features (e.g., and edge) matches the image.
How would this work?
Convolution
Convolution in the general mathematical sense is define as follows:

The convolution we deal with in deep learning is a simplified case. We want to compare two signals. Here are two visualizations, courtesy of Wikipedia, that help communicate how convolution emphasizes features:

Here's an animation (where we change \({\tau}\))

In one sense, the convolution captures and quantifies the pattern matching over space
If we perform this in two dimensions, we can achieve effects like highlighting edges:

The matrix here, also called a convolution kernel, is one of the functions we are convolving. Other convolution kernels can blur, "sharpen," etc.
So we'll drop in a number of convolution kernels, and the network will learn where to use them? Nope. Better than that.
We'll program in the idea of discrete convolution, and the network will learn what kernels extract meaningful features!
The values in a (fixed-size) convolution kernel matrix will be variables in our deep learning model. Although inuitively it seems like it would be hard to learn useful params, in fact, since those variables are used repeatedly across the image data, it "focuses" the error on a smallish number of parameters with a lot of influence -- so it should be vastly less expensive to train than just a huge fully connected layer like we discussed above.
This idea was developed in the late 1980s, and by 1989, Yann LeCun (at AT&T/Bell Labs) had built a practical high-accuracy system (used in the 1990s for processing handwritten checks and mail).
How do we hook this into our neural networks?
-
First, we can preserve the geometric properties of our data by "shaping" the vectors as 2D instead of 1D.
-
Then we'll create a layer whose value is not just activation applied to weighted sum of inputs, but instead it's the result of a dot-product (element-wise multiply and sum) between the kernel and a patch of the input vector (image).
- This value will be our "pre-activation" and optionally feed into an activation function (or "detector")

If we perform this operation at lots of positions over the image, we'll get lots of outputs, as many as one for every input pixel.

- So we'll add another layer that "picks" the highest convolution pattern match from nearby pixels, which
- makes our pattern match a little bit translation invariant (a fuzzy location match)
- reduces the number of outputs significantly
- This layer is commonly called a pooling layer, and if we pick the "maximum match" then it's a "max pooling" layer.

The end result is that the kernel or filter together with max pooling creates a value in a subsequent layer which represents the appearance of a pattern in a local area in a prior layer.
Again, the network will be given a number of "slots" for these filters and will learn (by minimizing error) what filter values produce meaningful features. This is the key insight into how modern image-recognition networks are able to generalize -- i.e., learn to tell 6s from 7s or cats from dogs.

Ok, let's build our first ConvNet:
First, we want to explicity shape our data into a 2-D configuration. We'll end up with a 4-D tensor where the first dimension is the training examples, then each example is 28x28 pixels, and we'll explicitly say it's 1-layer deep. (Why? with color images, we typically process over 3 or 4 channels in this last dimension)
A step by step animation follows: * http://cs231n.github.io/assets/conv-demo/index.html
train_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-train.txt"
test_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-test.txt"
X_train, y_train = sklearn.datasets.load_svmlight_file(train_libsvm, n_features=784)
X_train = X_train.toarray()
X_test, y_test = sklearn.datasets.load_svmlight_file(test_libsvm, n_features=784)
X_test = X_test.toarray()
X_train = X_train.reshape( (X_train.shape[0], 28, 28, 1) )
X_train = X_train.astype('float32')
X_train /= 255
y_train = to_categorical(y_train, num_classes=10)
X_test = X_test.reshape( (X_test.shape[0], 28, 28, 1) )
X_test = X_test.astype('float32')
X_test /= 255
y_test = to_categorical(y_test, num_classes=10)
Now the model:
from keras.layers import Dense, Dropout, Activation, Flatten, Conv2D, MaxPooling2D
model = Sequential()
model.add(Conv2D(8, # number of kernels
(4, 4), # kernel size
padding='valid', # no padding; output will be smaller than input
input_shape=(28, 28, 1)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(128))
model.add(Activation('relu')) # alternative syntax for applying activation
model.add(Dense(10))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
... and the training loop and output:
start = datetime.datetime.today()
history = model.fit(X_train, y_train, batch_size=128, epochs=8, verbose=2, validation_split=0.1)
scores = model.evaluate(X_test, y_test, verbose=1)
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
Train on 54000 samples, validate on 6000 samples
Epoch 1/8
- 21s - loss: 0.3099 - acc: 0.9143 - val_loss: 0.1025 - val_acc: 0.9728
Epoch 2/8
- 32s - loss: 0.0972 - acc: 0.9712 - val_loss: 0.0678 - val_acc: 0.9810
Epoch 3/8
- 35s - loss: 0.0653 - acc: 0.9803 - val_loss: 0.0545 - val_acc: 0.9858
Epoch 4/8
- 43s - loss: 0.0495 - acc: 0.9852 - val_loss: 0.0503 - val_acc: 0.9865
Epoch 5/8
- 42s - loss: 0.0392 - acc: 0.9884 - val_loss: 0.0503 - val_acc: 0.9845
Epoch 6/8
- 41s - loss: 0.0319 - acc: 0.9904 - val_loss: 0.0554 - val_acc: 0.9850
Epoch 7/8
- 40s - loss: 0.0250 - acc: 0.9927 - val_loss: 0.0437 - val_acc: 0.9885
Epoch 8/8
- 47s - loss: 0.0226 - acc: 0.9929 - val_loss: 0.0465 - val_acc: 0.9872
32/10000 [..............................] - ETA: 5s
160/10000 [..............................] - ETA: 5s
288/10000 [..............................] - ETA: 4s
416/10000 [>.............................] - ETA: 4s
544/10000 [>.............................] - ETA: 4s
672/10000 [=>............................] - ETA: 4s
800/10000 [=>............................] - ETA: 4s
928/10000 [=>............................] - ETA: 4s
1056/10000 [==>...........................] - ETA: 4s
1184/10000 [==>...........................] - ETA: 4s
1280/10000 [==>...........................] - ETA: 4s
1408/10000 [===>..........................] - ETA: 4s
1536/10000 [===>..........................] - ETA: 3s
1664/10000 [===>..........................] - ETA: 3s
1760/10000 [====>.........................] - ETA: 3s
1856/10000 [====>.........................] - ETA: 3s
1984/10000 [====>.........................] - ETA: 3s
2080/10000 [=====>........................] - ETA: 3s
2176/10000 [=====>........................] - ETA: 3s
2272/10000 [=====>........................] - ETA: 3s
2336/10000 [======>.......................] - ETA: 3s
2464/10000 [======>.......................] - ETA: 3s
2528/10000 [======>.......................] - ETA: 3s
2656/10000 [======>.......................] - ETA: 3s
2720/10000 [=======>......................] - ETA: 3s
2848/10000 [=======>......................] - ETA: 3s
2944/10000 [=======>......................] - ETA: 3s
3072/10000 [========>.....................] - ETA: 3s
3200/10000 [========>.....................] - ETA: 3s
3328/10000 [========>.....................] - ETA: 3s
3456/10000 [=========>....................] - ETA: 3s
3584/10000 [=========>....................] - ETA: 3s
3712/10000 [==========>...................] - ETA: 3s
3840/10000 [==========>...................] - ETA: 3s
3968/10000 [==========>...................] - ETA: 3s
4064/10000 [===========>..................] - ETA: 3s
4160/10000 [===========>..................] - ETA: 3s
4256/10000 [===========>..................] - ETA: 3s
4352/10000 [============>.................] - ETA: 2s
4416/10000 [============>.................] - ETA: 2s
4512/10000 [============>.................] - ETA: 2s
4576/10000 [============>.................] - ETA: 2s
4704/10000 [=============>................] - ETA: 2s
4800/10000 [=============>................] - ETA: 2s
4896/10000 [=============>................] - ETA: 2s
4928/10000 [=============>................] - ETA: 2s
5056/10000 [==============>...............] - ETA: 2s
5152/10000 [==============>...............] - ETA: 2s
5280/10000 [==============>...............] - ETA: 2s
5344/10000 [===============>..............] - ETA: 2s
5472/10000 [===============>..............] - ETA: 2s
5536/10000 [===============>..............] - ETA: 2s
5600/10000 [===============>..............] - ETA: 2s
5728/10000 [================>.............] - ETA: 2s
5792/10000 [================>.............] - ETA: 2s
5920/10000 [================>.............] - ETA: 2s
6016/10000 [=================>............] - ETA: 2s
6048/10000 [=================>............] - ETA: 2s
6144/10000 [=================>............] - ETA: 2s
6240/10000 [=================>............] - ETA: 2s
6336/10000 [==================>...........] - ETA: 2s
6464/10000 [==================>...........] - ETA: 2s
6592/10000 [==================>...........] - ETA: 2s
6720/10000 [===================>..........] - ETA: 1s
6816/10000 [===================>..........] - ETA: 1s
6944/10000 [===================>..........] - ETA: 1s
7040/10000 [====================>.........] - ETA: 1s
7168/10000 [====================>.........] - ETA: 1s
7296/10000 [====================>.........] - ETA: 1s
7424/10000 [=====================>........] - ETA: 1s
7552/10000 [=====================>........] - ETA: 1s
7648/10000 [=====================>........] - ETA: 1s
7744/10000 [======================>.......] - ETA: 1s
7840/10000 [======================>.......] - ETA: 1s
7936/10000 [======================>.......] - ETA: 1s
8064/10000 [=======================>......] - ETA: 1s
8128/10000 [=======================>......] - ETA: 1s
8256/10000 [=======================>......] - ETA: 1s
8352/10000 [========================>.....] - ETA: 0s
8480/10000 [========================>.....] - ETA: 0s
8576/10000 [========================>.....] - ETA: 0s
8672/10000 [=========================>....] - ETA: 0s
8768/10000 [=========================>....] - ETA: 0s
8864/10000 [=========================>....] - ETA: 0s
8960/10000 [=========================>....] - ETA: 0s
9056/10000 [==========================>...] - ETA: 0s
9152/10000 [==========================>...] - ETA: 0s
9216/10000 [==========================>...] - ETA: 0s
9344/10000 [===========================>..] - ETA: 0s
9472/10000 [===========================>..] - ETA: 0s
9568/10000 [===========================>..] - ETA: 0s
9632/10000 [===========================>..] - ETA: 0s
9760/10000 [============================>.] - ETA: 0s
9856/10000 [============================>.] - ETA: 0s
9952/10000 [============================>.] - ETA: 0s
10000/10000 [==============================] - 6s 583us/step
loss: 0.040131
acc: 0.986400
fig, ax = plt.subplots()
fig.set_size_inches((5,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
display(fig)
Our MNIST ConvNet
In our first convolutional MNIST experiment, we get to almost 99% validation accuracy in just a few epochs (a minutes or so on CPU)!
The training accuracy is effectively 100%, though, so we've almost completely overfit (i.e., memorized the training data) by this point and need to do a little work if we want to keep learning.
Let's add another convolutional layer:
model = Sequential()
model.add(Conv2D(8, # number of kernels
(4, 4), # kernel size
padding='valid',
input_shape=(28, 28, 1)))
model.add(Activation('relu'))
model.add(Conv2D(8, (4, 4)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(128))
model.add(Activation('relu'))
model.add(Dense(10))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(X_train, y_train, batch_size=128, epochs=15, verbose=2, validation_split=0.1)
scores = model.evaluate(X_test, y_test, verbose=1)
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
Train on 54000 samples, validate on 6000 samples
Epoch 1/15
- 104s - loss: 0.2681 - acc: 0.9224 - val_loss: 0.0784 - val_acc: 0.9768
Epoch 2/15
- 116s - loss: 0.0733 - acc: 0.9773 - val_loss: 0.0581 - val_acc: 0.9843
Epoch 3/15
- 114s - loss: 0.0511 - acc: 0.9847 - val_loss: 0.0435 - val_acc: 0.9873
Epoch 4/15
- 115s - loss: 0.0391 - acc: 0.9885 - val_loss: 0.0445 - val_acc: 0.9880
Epoch 5/15
- 105s - loss: 0.0307 - acc: 0.9904 - val_loss: 0.0446 - val_acc: 0.9890
Epoch 6/15
- 105s - loss: 0.0251 - acc: 0.9923 - val_loss: 0.0465 - val_acc: 0.9875
Epoch 7/15
- 102s - loss: 0.0193 - acc: 0.9936 - val_loss: 0.0409 - val_acc: 0.9892
Epoch 8/15
- 100s - loss: 0.0162 - acc: 0.9948 - val_loss: 0.0468 - val_acc: 0.9878
Epoch 9/15
- 103s - loss: 0.0138 - acc: 0.9956 - val_loss: 0.0447 - val_acc: 0.9893
Epoch 10/15
- 104s - loss: 0.0122 - acc: 0.9957 - val_loss: 0.0482 - val_acc: 0.9900
Epoch 11/15
- 102s - loss: 0.0097 - acc: 0.9969 - val_loss: 0.0480 - val_acc: 0.9895
Epoch 12/15
- 82s - loss: 0.0089 - acc: 0.9970 - val_loss: 0.0532 - val_acc: 0.9882
Epoch 13/15
- 93s - loss: 0.0080 - acc: 0.9973 - val_loss: 0.0423 - val_acc: 0.9913
Epoch 14/15
- 92s - loss: 0.0074 - acc: 0.9976 - val_loss: 0.0557 - val_acc: 0.9883
Epoch 15/15
- 92s - loss: 0.0043 - acc: 0.9987 - val_loss: 0.0529 - val_acc: 0.9902
32/10000 [..............................] - ETA: 4s
128/10000 [..............................] - ETA: 6s
256/10000 [..............................] - ETA: 5s
352/10000 [>.............................] - ETA: 6s
448/10000 [>.............................] - ETA: 6s
512/10000 [>.............................] - ETA: 6s
608/10000 [>.............................] - ETA: 6s
736/10000 [=>............................] - ETA: 5s
800/10000 [=>............................] - ETA: 6s
896/10000 [=>............................] - ETA: 5s
1024/10000 [==>...........................] - ETA: 5s
1120/10000 [==>...........................] - ETA: 5s
1216/10000 [==>...........................] - ETA: 5s
1312/10000 [==>...........................] - ETA: 5s
1408/10000 [===>..........................] - ETA: 5s
1504/10000 [===>..........................] - ETA: 5s
1600/10000 [===>..........................] - ETA: 5s
1664/10000 [===>..........................] - ETA: 5s
1760/10000 [====>.........................] - ETA: 5s
1856/10000 [====>.........................] - ETA: 5s
1952/10000 [====>.........................] - ETA: 5s
2048/10000 [=====>........................] - ETA: 5s
2144/10000 [=====>........................] - ETA: 4s
2240/10000 [=====>........................] - ETA: 4s
2336/10000 [======>.......................] - ETA: 4s
2432/10000 [======>.......................] - ETA: 4s
2496/10000 [======>.......................] - ETA: 4s
2592/10000 [======>.......................] - ETA: 4s
2688/10000 [=======>......................] - ETA: 4s
2784/10000 [=======>......................] - ETA: 4s
2880/10000 [=======>......................] - ETA: 4s
2976/10000 [=======>......................] - ETA: 4s
3072/10000 [========>.....................] - ETA: 4s
3168/10000 [========>.....................] - ETA: 4s
3232/10000 [========>.....................] - ETA: 4s
3360/10000 [=========>....................] - ETA: 4s
3456/10000 [=========>....................] - ETA: 4s
3552/10000 [=========>....................] - ETA: 4s
3648/10000 [=========>....................] - ETA: 3s
3776/10000 [==========>...................] - ETA: 3s
3872/10000 [==========>...................] - ETA: 3s
3968/10000 [==========>...................] - ETA: 3s
4096/10000 [===========>..................] - ETA: 3s
4192/10000 [===========>..................] - ETA: 3s
4288/10000 [===========>..................] - ETA: 3s
4384/10000 [============>.................] - ETA: 3s
4480/10000 [============>.................] - ETA: 3s
4576/10000 [============>.................] - ETA: 3s
4672/10000 [=============>................] - ETA: 3s
4768/10000 [=============>................] - ETA: 3s
4864/10000 [=============>................] - ETA: 3s
4960/10000 [=============>................] - ETA: 3s
5024/10000 [==============>...............] - ETA: 3s
5120/10000 [==============>...............] - ETA: 3s
5216/10000 [==============>...............] - ETA: 3s
5312/10000 [==============>...............] - ETA: 2s
5408/10000 [===============>..............] - ETA: 2s
5504/10000 [===============>..............] - ETA: 2s
5600/10000 [===============>..............] - ETA: 2s
5696/10000 [================>.............] - ETA: 2s
5792/10000 [================>.............] - ETA: 2s
5920/10000 [================>.............] - ETA: 2s
6016/10000 [=================>............] - ETA: 2s
6080/10000 [=================>............] - ETA: 2s
6176/10000 [=================>............] - ETA: 2s
6272/10000 [=================>............] - ETA: 2s
6368/10000 [==================>...........] - ETA: 2s
6464/10000 [==================>...........] - ETA: 2s
6560/10000 [==================>...........] - ETA: 2s
6656/10000 [==================>...........] - ETA: 2s
6752/10000 [===================>..........] - ETA: 2s
6848/10000 [===================>..........] - ETA: 1s
6912/10000 [===================>..........] - ETA: 1s
7008/10000 [====================>.........] - ETA: 1s
7104/10000 [====================>.........] - ETA: 1s
7200/10000 [====================>.........] - ETA: 1s
7328/10000 [====================>.........] - ETA: 1s
7424/10000 [=====================>........] - ETA: 1s
7552/10000 [=====================>........] - ETA: 1s
7648/10000 [=====================>........] - ETA: 1s
7712/10000 [======================>.......] - ETA: 1s
7776/10000 [======================>.......] - ETA: 1s
7872/10000 [======================>.......] - ETA: 1s
7968/10000 [======================>.......] - ETA: 1s
8032/10000 [=======================>......] - ETA: 1s
8128/10000 [=======================>......] - ETA: 1s
8224/10000 [=======================>......] - ETA: 1s
8288/10000 [=======================>......] - ETA: 1s
8352/10000 [========================>.....] - ETA: 1s
8448/10000 [========================>.....] - ETA: 1s
8544/10000 [========================>.....] - ETA: 0s
8640/10000 [========================>.....] - ETA: 0s
8704/10000 [=========================>....] - ETA: 0s
8800/10000 [=========================>....] - ETA: 0s
8864/10000 [=========================>....] - ETA: 0s
8992/10000 [=========================>....] - ETA: 0s
9056/10000 [==========================>...] - ETA: 0s
9152/10000 [==========================>...] - ETA: 0s
9248/10000 [==========================>...] - ETA: 0s
9344/10000 [===========================>..] - ETA: 0s
9408/10000 [===========================>..] - ETA: 0s
9504/10000 [===========================>..] - ETA: 0s
9600/10000 [===========================>..] - ETA: 0s
9696/10000 [============================>.] - ETA: 0s
9792/10000 [============================>.] - ETA: 0s
9888/10000 [============================>.] - ETA: 0s
9984/10000 [============================>.] - ETA: 0s
10000/10000 [==============================] - 7s 663us/step
loss: 0.040078
acc: 0.990700
While that's running, let's look at a number of "famous" convolutional networks!
LeNet (Yann LeCun, 1998)



Back to our labs: Still Overfitting
We're making progress on our test error -- about 99% -- but just a bit for all the additional time, due to the network overfitting the data.
There are a variety of techniques we can take to counter this -- forms of regularization.
Let's try a relatively simple solution solution that works surprisingly well: add a pair of Dropout filters, a layer that randomly omits a fraction of neurons from each training batch (thus exposing each neuron to only part of the training data).
We'll add more convolution kernels but shrink them to 3x3 as well.
model = Sequential()
model.add(Conv2D(32, # number of kernels
(3, 3), # kernel size
padding='valid',
input_shape=(28, 28, 1)))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(rate=1-0.25)) # <- regularize, new parameter rate added (rate=1-keep_prob)
model.add(Flatten())
model.add(Dense(128))
model.add(Activation('relu'))
model.add(Dropout(rate=1-0.5)) # <-regularize, new parameter rate added (rate=1-keep_prob)
model.add(Dense(10))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(X_train, y_train, batch_size=128, epochs=15, verbose=2)
scores = model.evaluate(X_test, y_test, verbose=2)
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:3733: calling dropout (from tensorflow.python.ops.nn_ops) with keep_prob is deprecated and will be removed in a future version.
Instructions for updating:
Please use `rate` instead of `keep_prob`. Rate should be set to `rate = 1 - keep_prob`.
Epoch 1/15
- 370s - loss: 0.3865 - acc: 0.8783
Epoch 2/15
- 353s - loss: 0.1604 - acc: 0.9522
Epoch 3/15
- 334s - loss: 0.1259 - acc: 0.9617
Epoch 4/15
- 337s - loss: 0.1071 - acc: 0.9666
Epoch 5/15
- 265s - loss: 0.0982 - acc: 0.9699
Epoch 6/15
- 250s - loss: 0.0923 - acc: 0.9716
Epoch 7/15
- 244s - loss: 0.0845 - acc: 0.9740
Epoch 8/15
- 247s - loss: 0.0811 - acc: 0.9747
Epoch 9/15
- 246s - loss: 0.0767 - acc: 0.9766
Epoch 10/15
- 246s - loss: 0.0749 - acc: 0.9764
Epoch 11/15
- 247s - loss: 0.0708 - acc: 0.9776
Epoch 12/15
- 244s - loss: 0.0698 - acc: 0.9779
Epoch 13/15
- 248s - loss: 0.0667 - acc: 0.9794
Epoch 14/15
- 244s - loss: 0.0653 - acc: 0.9799
Epoch 15/15
- 249s - loss: 0.0645 - acc: 0.9801
loss: 0.023579
acc: 0.991300
GoogLeNet (2014)

"Inception" layer: parallel convolutions at different resolutions
Residual Networks (2015-)
Skip layers to improve training (error propagation). Residual layers learn from details at multiple previous layers.

ASIDE: Atrous / Dilated Convolutions
An atrous or dilated convolution is a convolution filter with "holes" in it. Effectively, it is a way to enlarge the filter spatially while not adding as many parameters or attending to every element in the input.
Why? Covering a larger input volume allows recognizing coarser-grained patterns; restricting the number of parameters is a way of regularizing or constraining the capacity of the model, making training easier.
Lab Wrapup
From the last lab, you should have a test accuracy of over 99.1%
For one more activity, try changing the optimizer to old-school "sgd" -- just to see how far we've come with these modern gradient descent techniques in the last few years.
Accuracy will end up noticeably worse ... about 96-97% test accuracy. Two key takeaways:
- Without a good optimizer, even a very powerful network design may not achieve results
- In fact, we could replace the word "optimizer" there with
- initialization
- activation
- regularization
- (etc.)
- All of these elements we've been working with operate together in a complex way to determine final performance
Of course this world evolves fast - see the new kid in the CNN block -- capsule networks
Hinton: “The pooling operation used in convolutional neural networks is a big mistake and the fact that it works so well is a disaster.”
Well worth the 8 minute read: * https://medium.com/ai%C2%B3-theory-practice-business/understanding-hintons-capsule-networks-part-i-intuition-b4b559d1159b
To understand deeper: * original paper: https://arxiv.org/abs/1710.09829
More resources
- http://www.wildml.com/2015/12/implementing-a-cnn-for-text-classification-in-tensorflow/
- https://openai.com/
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
As we dive into more hands-on works, let's recap some basic guidelines:
-
Structure of your network is the first thing to work with, before worrying about the precise number of neurons, size of convolution filters etc.
-
"Business records" or fairly (ideally?) uncorrelated predictors -- use Dense Perceptron Layer(s)
-
Data that has 2-D patterns: 2D Convolution layer(s)
-
For activation of hidden layers, when in doubt, use ReLU
-
Output:
- Regression: 1 neuron with linear activation
- For k-way classification: k neurons with softmax activation
-
Deeper networks are "smarter" than wider networks (in terms of abstraction)
-
More neurons & layers \(\to\) more capacity \(\to\) more data \(\to\) more regularization (to prevent overfitting)
-
If you don't have any specific reason not to use the "adam" optimizer, use that one
-
Errors:
- For regression or "wide" content matching (e.g., large image similarity), use mean-square-error;
- For classification or narrow content matching, use cross-entropy
- As you simplify and abstract from your raw data, you should need less features/parameters, so your layers probably become smaller and simpler.
As a baseline, let's start a lab running with what we already know.
We'll take our deep feed-forward multilayer perceptron network, with ReLU activations and reasonable initializations, and apply it to learning the MNIST digits.
The main part of the code looks like the following (full code you can run is in the next cell):
# imports, setup, load data sets
model = Sequential()
model.add(Dense(20, input_dim=784, kernel_initializer='normal', activation='relu'))
model.add(Dense(15, kernel_initializer='normal', activation='relu'))
model.add(Dense(10, kernel_initializer='normal', activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['categorical_accuracy'])
categorical_labels = to_categorical(y_train, num_classes=10)
history = model.fit(X_train, categorical_labels, epochs=100, batch_size=100)
# print metrics, plot errors
Note the changes, which are largely about building a classifier instead of a regression model:
- Output layer has one neuron per category, with softmax activation
- Loss function is cross-entropy loss
- Accuracy metric is categorical accuracy
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import to_categorical
import sklearn.datasets
import datetime
import matplotlib.pyplot as plt
import numpy as np
train_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-train.txt"
test_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-test.txt"
X_train, y_train = sklearn.datasets.load_svmlight_file(train_libsvm, n_features=784)
X_train = X_train.toarray()
X_test, y_test = sklearn.datasets.load_svmlight_file(test_libsvm, n_features=784)
X_test = X_test.toarray()
model = Sequential()
model.add(Dense(20, input_dim=784, kernel_initializer='normal', activation='relu'))
model.add(Dense(15, kernel_initializer='normal', activation='relu'))
model.add(Dense(10, kernel_initializer='normal', activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['categorical_accuracy'])
categorical_labels = to_categorical(y_train, num_classes=10)
start = datetime.datetime.today()
history = model.fit(X_train, categorical_labels, epochs=40, batch_size=100, validation_split=0.1, verbose=2)
scores = model.evaluate(X_test, to_categorical(y_test, num_classes=10))
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
print ("Start: " + str(start))
end = datetime.datetime.today()
print ("End: " + str(end))
print ("Elapse: " + str(end-start))
Using TensorFlow backend.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 54000 samples, validate on 6000 samples
Epoch 1/40
- 3s - loss: 0.5395 - categorical_accuracy: 0.8275 - val_loss: 0.2016 - val_categorical_accuracy: 0.9428
Epoch 2/40
- 2s - loss: 0.2209 - categorical_accuracy: 0.9353 - val_loss: 0.1561 - val_categorical_accuracy: 0.9545
Epoch 3/40
- 2s - loss: 0.1777 - categorical_accuracy: 0.9466 - val_loss: 0.1491 - val_categorical_accuracy: 0.9568
Epoch 4/40
- 2s - loss: 0.1561 - categorical_accuracy: 0.9532 - val_loss: 0.1335 - val_categorical_accuracy: 0.9612
Epoch 5/40
- 2s - loss: 0.1376 - categorical_accuracy: 0.9581 - val_loss: 0.1303 - val_categorical_accuracy: 0.9640
Epoch 6/40
- 3s - loss: 0.1252 - categorical_accuracy: 0.9621 - val_loss: 0.1334 - val_categorical_accuracy: 0.9612
Epoch 7/40
- 3s - loss: 0.1171 - categorical_accuracy: 0.9641 - val_loss: 0.1292 - val_categorical_accuracy: 0.9650
Epoch 8/40
- 3s - loss: 0.1112 - categorical_accuracy: 0.9657 - val_loss: 0.1388 - val_categorical_accuracy: 0.9638
Epoch 9/40
- 3s - loss: 0.1054 - categorical_accuracy: 0.9683 - val_loss: 0.1241 - val_categorical_accuracy: 0.9652
Epoch 10/40
- 2s - loss: 0.0993 - categorical_accuracy: 0.9693 - val_loss: 0.1314 - val_categorical_accuracy: 0.9652
Epoch 11/40
- 3s - loss: 0.1004 - categorical_accuracy: 0.9690 - val_loss: 0.1426 - val_categorical_accuracy: 0.9637
Epoch 12/40
- 3s - loss: 0.0932 - categorical_accuracy: 0.9713 - val_loss: 0.1409 - val_categorical_accuracy: 0.9653
Epoch 13/40
- 3s - loss: 0.0915 - categorical_accuracy: 0.9716 - val_loss: 0.1403 - val_categorical_accuracy: 0.9628
Epoch 14/40
- 3s - loss: 0.0883 - categorical_accuracy: 0.9733 - val_loss: 0.1347 - val_categorical_accuracy: 0.9662
Epoch 15/40
- 3s - loss: 0.0855 - categorical_accuracy: 0.9737 - val_loss: 0.1371 - val_categorical_accuracy: 0.9683
Epoch 16/40
- 3s - loss: 0.0855 - categorical_accuracy: 0.9736 - val_loss: 0.1453 - val_categorical_accuracy: 0.9663
Epoch 17/40
- 3s - loss: 0.0805 - categorical_accuracy: 0.9744 - val_loss: 0.1374 - val_categorical_accuracy: 0.9665
Epoch 18/40
- 2s - loss: 0.0807 - categorical_accuracy: 0.9756 - val_loss: 0.1348 - val_categorical_accuracy: 0.9685
Epoch 19/40
- 2s - loss: 0.0809 - categorical_accuracy: 0.9748 - val_loss: 0.1433 - val_categorical_accuracy: 0.9662
Epoch 20/40
- 2s - loss: 0.0752 - categorical_accuracy: 0.9766 - val_loss: 0.1415 - val_categorical_accuracy: 0.9667
Epoch 21/40
- 3s - loss: 0.0736 - categorical_accuracy: 0.9771 - val_loss: 0.1575 - val_categorical_accuracy: 0.9650
Epoch 22/40
- 3s - loss: 0.0743 - categorical_accuracy: 0.9768 - val_loss: 0.1517 - val_categorical_accuracy: 0.9670
Epoch 23/40
- 3s - loss: 0.0727 - categorical_accuracy: 0.9770 - val_loss: 0.1458 - val_categorical_accuracy: 0.9680
Epoch 24/40
- 3s - loss: 0.0710 - categorical_accuracy: 0.9778 - val_loss: 0.1618 - val_categorical_accuracy: 0.9645
Epoch 25/40
- 3s - loss: 0.0687 - categorical_accuracy: 0.9789 - val_loss: 0.1499 - val_categorical_accuracy: 0.9650
Epoch 26/40
- 3s - loss: 0.0680 - categorical_accuracy: 0.9787 - val_loss: 0.1448 - val_categorical_accuracy: 0.9685
Epoch 27/40
- 3s - loss: 0.0685 - categorical_accuracy: 0.9788 - val_loss: 0.1533 - val_categorical_accuracy: 0.9665
Epoch 28/40
- 3s - loss: 0.0677 - categorical_accuracy: 0.9786 - val_loss: 0.1668 - val_categorical_accuracy: 0.9640
Epoch 29/40
- 3s - loss: 0.0631 - categorical_accuracy: 0.9809 - val_loss: 0.1739 - val_categorical_accuracy: 0.9632
Epoch 30/40
- 3s - loss: 0.0687 - categorical_accuracy: 0.9780 - val_loss: 0.1584 - val_categorical_accuracy: 0.9653
Epoch 31/40
- 3s - loss: 0.0644 - categorical_accuracy: 0.9799 - val_loss: 0.1724 - val_categorical_accuracy: 0.9678
Epoch 32/40
- 3s - loss: 0.0621 - categorical_accuracy: 0.9807 - val_loss: 0.1709 - val_categorical_accuracy: 0.9648
Epoch 33/40
- 4s - loss: 0.0618 - categorical_accuracy: 0.9804 - val_loss: 0.2055 - val_categorical_accuracy: 0.9592
Epoch 34/40
- 4s - loss: 0.0620 - categorical_accuracy: 0.9804 - val_loss: 0.1752 - val_categorical_accuracy: 0.9650
Epoch 35/40
- 3s - loss: 0.0586 - categorical_accuracy: 0.9820 - val_loss: 0.1726 - val_categorical_accuracy: 0.9643
Epoch 36/40
- 3s - loss: 0.0606 - categorical_accuracy: 0.9804 - val_loss: 0.1851 - val_categorical_accuracy: 0.9622
Epoch 37/40
- 3s - loss: 0.0592 - categorical_accuracy: 0.9814 - val_loss: 0.1820 - val_categorical_accuracy: 0.9643
Epoch 38/40
- 3s - loss: 0.0573 - categorical_accuracy: 0.9823 - val_loss: 0.1874 - val_categorical_accuracy: 0.9638
Epoch 39/40
- 3s - loss: 0.0609 - categorical_accuracy: 0.9808 - val_loss: 0.1843 - val_categorical_accuracy: 0.9617
Epoch 40/40
- 3s - loss: 0.0573 - categorical_accuracy: 0.9823 - val_loss: 0.1774 - val_categorical_accuracy: 0.9628
32/10000 [..............................] - ETA: 0s
384/10000 [>.............................] - ETA: 1s
1088/10000 [==>...........................] - ETA: 0s
1856/10000 [====>.........................] - ETA: 0s
2880/10000 [=======>......................] - ETA: 0s
3552/10000 [=========>....................] - ETA: 0s
4352/10000 [============>.................] - ETA: 0s
4832/10000 [=============>................] - ETA: 0s
5536/10000 [===============>..............] - ETA: 0s
6368/10000 [==================>...........] - ETA: 0s
6752/10000 [===================>..........] - ETA: 0s
7296/10000 [====================>.........] - ETA: 0s
8064/10000 [=======================>......] - ETA: 0s
9152/10000 [==========================>...] - ETA: 0s
10000/10000 [==============================] - 1s 73us/step
loss: 0.213623
categorical_accuracy: 0.956900
Start: 2021-02-10 10:21:41.350257
End: 2021-02-10 10:23:35.823391
Elapse: 0:01:54.473134
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
fig.set_size_inches((5,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
display(fig)
What are the big takeaways from this experiment?
- We get pretty impressive "apparent error" accuracy right from the start! A small network gets us to training accuracy 97% by epoch 20
- The model appears to continue to learn if we let it run, although it does slow down and oscillate a bit.
- Our test accuracy is about 95% after 5 epochs and never gets better ... it gets worse!
- Therefore, we are overfitting very quickly... most of the "training" turns out to be a waste.
- For what it's worth, we get 95% accuracy without much work.
This is not terrible compared to other, non-neural-network approaches to the problem. After all, we could probably tweak this a bit and do even better.
But we talked about using deep learning to solve "95%" problems or "98%" problems ... where one error in 20, or 50 simply won't work. If we can get to "multiple nines" of accuracy, then we can do things like automate mail sorting and translation, create cars that react properly (all the time) to street signs, and control systems for robots or drones that function autonomously.
You Try Now!
Try two more experiments (try them separately):
- Add a third, hidden layer.
- Increase the size of the hidden layers.
Adding another layer slows things down a little (why?) but doesn't seem to make a difference in accuracy.
Adding a lot more neurons into the first topology slows things down significantly -- 10x as many neurons, and only a marginal increase in accuracy. Notice also (in the plot) that the learning clearly degrades after epoch 50 or so.
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Try out the first ConvNet -- the one we looked at earlier.
This code is the same, but we'll run to 20 epochs so we can get a better feel for fitting/validation/overfitting trend.
from keras.utils import to_categorical
import sklearn.datasets
train_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-train.txt"
test_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-test.txt"
X_train, y_train = sklearn.datasets.load_svmlight_file(train_libsvm, n_features=784)
X_train = X_train.toarray()
X_test, y_test = sklearn.datasets.load_svmlight_file(test_libsvm, n_features=784)
X_test = X_test.toarray()
X_train = X_train.reshape( (X_train.shape[0], 28, 28, 1) )
X_train = X_train.astype('float32')
X_train /= 255
y_train = to_categorical(y_train, num_classes=10)
X_test = X_test.reshape( (X_test.shape[0], 28, 28, 1) )
X_test = X_test.astype('float32')
X_test /= 255
y_test = to_categorical(y_test, num_classes=10)
Using TensorFlow backend.
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten, Conv2D, MaxPooling2D
model = Sequential()
model.add(Conv2D(8, # number of kernels
(4, 4), # kernel size
padding='valid', # no padding; output will be smaller than input
input_shape=(28, 28, 1)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(128))
model.add(Activation('relu')) # alternative syntax for applying activation
model.add(Dense(10))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(X_train, y_train, batch_size=128, epochs=20, verbose=2, validation_split=0.1)
scores = model.evaluate(X_test, y_test, verbose=1)
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 54000 samples, validate on 6000 samples
Epoch 1/20
- 43s - loss: 0.2952 - acc: 0.9172 - val_loss: 0.1003 - val_acc: 0.9703
Epoch 2/20
- 43s - loss: 0.0869 - acc: 0.9739 - val_loss: 0.0626 - val_acc: 0.9837
Epoch 3/20
- 42s - loss: 0.0613 - acc: 0.9814 - val_loss: 0.0589 - val_acc: 0.9833
Epoch 4/20
- 41s - loss: 0.0474 - acc: 0.9859 - val_loss: 0.0540 - val_acc: 0.9857
Epoch 5/20
- 44s - loss: 0.0394 - acc: 0.9878 - val_loss: 0.0480 - val_acc: 0.9862
Epoch 6/20
- 48s - loss: 0.0315 - acc: 0.9906 - val_loss: 0.0483 - val_acc: 0.9870
Epoch 7/20
- 48s - loss: 0.0276 - acc: 0.9913 - val_loss: 0.0535 - val_acc: 0.9873
Epoch 8/20
- 55s - loss: 0.0223 - acc: 0.9932 - val_loss: 0.0455 - val_acc: 0.9868
Epoch 9/20
- 58s - loss: 0.0179 - acc: 0.9947 - val_loss: 0.0521 - val_acc: 0.9873
Epoch 10/20
- 57s - loss: 0.0172 - acc: 0.9946 - val_loss: 0.0462 - val_acc: 0.9887
Epoch 11/20
- 56s - loss: 0.0150 - acc: 0.9953 - val_loss: 0.0469 - val_acc: 0.9887
Epoch 12/20
- 57s - loss: 0.0124 - acc: 0.9962 - val_loss: 0.0479 - val_acc: 0.9887
Epoch 13/20
- 57s - loss: 0.0099 - acc: 0.9969 - val_loss: 0.0528 - val_acc: 0.9873
Epoch 14/20
- 57s - loss: 0.0091 - acc: 0.9973 - val_loss: 0.0607 - val_acc: 0.9827
Epoch 15/20
- 53s - loss: 0.0072 - acc: 0.9981 - val_loss: 0.0548 - val_acc: 0.9887
Epoch 16/20
- 51s - loss: 0.0071 - acc: 0.9979 - val_loss: 0.0525 - val_acc: 0.9892
Epoch 17/20
- 52s - loss: 0.0055 - acc: 0.9982 - val_loss: 0.0512 - val_acc: 0.9877
Epoch 18/20
- 52s - loss: 0.0073 - acc: 0.9977 - val_loss: 0.0559 - val_acc: 0.9885
Epoch 19/20
- 52s - loss: 0.0037 - acc: 0.9990 - val_loss: 0.0522 - val_acc: 0.9893
Epoch 20/20
- 51s - loss: 0.0073 - acc: 0.9976 - val_loss: 0.0938 - val_acc: 0.9792
32/10000 [..............................] - ETA: 5s
128/10000 [..............................] - ETA: 5s
224/10000 [..............................] - ETA: 5s
352/10000 [>.............................] - ETA: 5s
448/10000 [>.............................] - ETA: 5s
576/10000 [>.............................] - ETA: 4s
704/10000 [=>............................] - ETA: 4s
832/10000 [=>............................] - ETA: 4s
960/10000 [=>............................] - ETA: 4s
1056/10000 [==>...........................] - ETA: 4s
1152/10000 [==>...........................] - ETA: 4s
1248/10000 [==>...........................] - ETA: 4s
1312/10000 [==>...........................] - ETA: 4s
1440/10000 [===>..........................] - ETA: 4s
1568/10000 [===>..........................] - ETA: 4s
1632/10000 [===>..........................] - ETA: 4s
1760/10000 [====>.........................] - ETA: 4s
1888/10000 [====>.........................] - ETA: 4s
2016/10000 [=====>........................] - ETA: 4s
2144/10000 [=====>........................] - ETA: 4s
2240/10000 [=====>........................] - ETA: 4s
2368/10000 [======>.......................] - ETA: 4s
2464/10000 [======>.......................] - ETA: 4s
2560/10000 [======>.......................] - ETA: 4s
2624/10000 [======>.......................] - ETA: 4s
2752/10000 [=======>......................] - ETA: 4s
2848/10000 [=======>......................] - ETA: 4s
2944/10000 [=======>......................] - ETA: 4s
3072/10000 [========>.....................] - ETA: 4s
3168/10000 [========>.....................] - ETA: 3s
3264/10000 [========>.....................] - ETA: 3s
3328/10000 [========>.....................] - ETA: 3s
3456/10000 [=========>....................] - ETA: 3s
3584/10000 [=========>....................] - ETA: 3s
3744/10000 [==========>...................] - ETA: 3s
3840/10000 [==========>...................] - ETA: 3s
3968/10000 [==========>...................] - ETA: 3s
4064/10000 [===========>..................] - ETA: 3s
4160/10000 [===========>..................] - ETA: 3s
4256/10000 [===========>..................] - ETA: 3s
4352/10000 [============>.................] - ETA: 3s
4448/10000 [============>.................] - ETA: 3s
4544/10000 [============>.................] - ETA: 3s
4672/10000 [=============>................] - ETA: 3s
4800/10000 [=============>................] - ETA: 2s
4928/10000 [=============>................] - ETA: 2s
5024/10000 [==============>...............] - ETA: 2s
5120/10000 [==============>...............] - ETA: 2s
5248/10000 [==============>...............] - ETA: 2s
5376/10000 [===============>..............] - ETA: 2s
5504/10000 [===============>..............] - ETA: 2s
5600/10000 [===============>..............] - ETA: 2s
5696/10000 [================>.............] - ETA: 2s
5856/10000 [================>.............] - ETA: 2s
5984/10000 [================>.............] - ETA: 2s
6080/10000 [=================>............] - ETA: 2s
6176/10000 [=================>............] - ETA: 2s
6272/10000 [=================>............] - ETA: 2s
6400/10000 [==================>...........] - ETA: 1s
6528/10000 [==================>...........] - ETA: 1s
6624/10000 [==================>...........] - ETA: 1s
6720/10000 [===================>..........] - ETA: 1s
6816/10000 [===================>..........] - ETA: 1s
6944/10000 [===================>..........] - ETA: 1s
7104/10000 [====================>.........] - ETA: 1s
7168/10000 [====================>.........] - ETA: 1s
7296/10000 [====================>.........] - ETA: 1s
7424/10000 [=====================>........] - ETA: 1s
7552/10000 [=====================>........] - ETA: 1s
7616/10000 [=====================>........] - ETA: 1s
7744/10000 [======================>.......] - ETA: 1s
7840/10000 [======================>.......] - ETA: 1s
7968/10000 [======================>.......] - ETA: 1s
8064/10000 [=======================>......] - ETA: 1s
8192/10000 [=======================>......] - ETA: 0s
8288/10000 [=======================>......] - ETA: 0s
8384/10000 [========================>.....] - ETA: 0s
8512/10000 [========================>.....] - ETA: 0s
8640/10000 [========================>.....] - ETA: 0s
8736/10000 [=========================>....] - ETA: 0s
8864/10000 [=========================>....] - ETA: 0s
8960/10000 [=========================>....] - ETA: 0s
9088/10000 [==========================>...] - ETA: 0s
9216/10000 [==========================>...] - ETA: 0s
9344/10000 [===========================>..] - ETA: 0s
9472/10000 [===========================>..] - ETA: 0s
9568/10000 [===========================>..] - ETA: 0s
9664/10000 [===========================>..] - ETA: 0s
9760/10000 [============================>.] - ETA: 0s
9856/10000 [============================>.] - ETA: 0s
9952/10000 [============================>.] - ETA: 0s
10000/10000 [==============================] - 6s 551us/step
loss: 0.092008
acc: 0.978300
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
fig.set_size_inches((5,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
display(fig)
Next, let's try adding another convolutional layer:
model = Sequential()
model.add(Conv2D(8, # number of kernels
(4, 4), # kernel size
padding='valid',
input_shape=(28, 28, 1)))
model.add(Activation('relu'))
model.add(Conv2D(8, (4, 4))) # <-- additional Conv layer
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(128))
model.add(Activation('relu'))
model.add(Dense(10))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(X_train, y_train, batch_size=128, epochs=15, verbose=2, validation_split=0.1)
scores = model.evaluate(X_test, y_test, verbose=1)
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
Train on 54000 samples, validate on 6000 samples
Epoch 1/15
- 104s - loss: 0.2522 - acc: 0.9276 - val_loss: 0.0790 - val_acc: 0.9803
Epoch 2/15
- 103s - loss: 0.0719 - acc: 0.9780 - val_loss: 0.0605 - val_acc: 0.9827
Epoch 3/15
- 103s - loss: 0.0488 - acc: 0.9848 - val_loss: 0.0586 - val_acc: 0.9842
Epoch 4/15
- 95s - loss: 0.0393 - acc: 0.9879 - val_loss: 0.0468 - val_acc: 0.9885
Epoch 5/15
- 86s - loss: 0.0309 - acc: 0.9903 - val_loss: 0.0451 - val_acc: 0.9888
Epoch 6/15
- 94s - loss: 0.0252 - acc: 0.9923 - val_loss: 0.0449 - val_acc: 0.9883
Epoch 7/15
- 91s - loss: 0.0195 - acc: 0.9938 - val_loss: 0.0626 - val_acc: 0.9875
Epoch 8/15
- 93s - loss: 0.0146 - acc: 0.9954 - val_loss: 0.0500 - val_acc: 0.9885
Epoch 9/15
- 94s - loss: 0.0122 - acc: 0.9964 - val_loss: 0.0478 - val_acc: 0.9897
Epoch 10/15
- 95s - loss: 0.0113 - acc: 0.9962 - val_loss: 0.0515 - val_acc: 0.9895
Epoch 11/15
- 96s - loss: 0.0085 - acc: 0.9971 - val_loss: 0.0796 - val_acc: 0.9860
Epoch 12/15
- 94s - loss: 0.0091 - acc: 0.9967 - val_loss: 0.0535 - val_acc: 0.9878
Epoch 13/15
- 94s - loss: 0.0066 - acc: 0.9979 - val_loss: 0.0672 - val_acc: 0.9873
Epoch 14/15
- 95s - loss: 0.0064 - acc: 0.9977 - val_loss: 0.0594 - val_acc: 0.9883
Epoch 15/15
- 88s - loss: 0.0055 - acc: 0.9983 - val_loss: 0.0679 - val_acc: 0.9877
32/10000 [..............................] - ETA: 6s
128/10000 [..............................] - ETA: 6s
224/10000 [..............................] - ETA: 6s
320/10000 [..............................] - ETA: 5s
448/10000 [>.............................] - ETA: 5s
512/10000 [>.............................] - ETA: 6s
608/10000 [>.............................] - ETA: 6s
704/10000 [=>............................] - ETA: 6s
768/10000 [=>............................] - ETA: 6s
864/10000 [=>............................] - ETA: 6s
960/10000 [=>............................] - ETA: 6s
1056/10000 [==>...........................] - ETA: 6s
1120/10000 [==>...........................] - ETA: 6s
1184/10000 [==>...........................] - ETA: 6s
1312/10000 [==>...........................] - ETA: 6s
1408/10000 [===>..........................] - ETA: 6s
1472/10000 [===>..........................] - ETA: 6s
1568/10000 [===>..........................] - ETA: 5s
1664/10000 [===>..........................] - ETA: 5s
1728/10000 [====>.........................] - ETA: 5s
1824/10000 [====>.........................] - ETA: 5s
1920/10000 [====>.........................] - ETA: 5s
1984/10000 [====>.........................] - ETA: 5s
2080/10000 [=====>........................] - ETA: 5s
2176/10000 [=====>........................] - ETA: 5s
2240/10000 [=====>........................] - ETA: 5s
2336/10000 [======>.......................] - ETA: 5s
2400/10000 [======>.......................] - ETA: 5s
2464/10000 [======>.......................] - ETA: 5s
2560/10000 [======>.......................] - ETA: 5s
2656/10000 [======>.......................] - ETA: 5s
2752/10000 [=======>......................] - ETA: 5s
2848/10000 [=======>......................] - ETA: 5s
2976/10000 [=======>......................] - ETA: 4s
3072/10000 [========>.....................] - ETA: 4s
3168/10000 [========>.....................] - ETA: 4s
3232/10000 [========>.....................] - ETA: 4s
3296/10000 [========>.....................] - ETA: 4s
3392/10000 [=========>....................] - ETA: 4s
3488/10000 [=========>....................] - ETA: 4s
3552/10000 [=========>....................] - ETA: 4s
3616/10000 [=========>....................] - ETA: 4s
3712/10000 [==========>...................] - ETA: 4s
3808/10000 [==========>...................] - ETA: 4s
3904/10000 [==========>...................] - ETA: 4s
3968/10000 [==========>...................] - ETA: 4s
4064/10000 [===========>..................] - ETA: 4s
4160/10000 [===========>..................] - ETA: 4s
4256/10000 [===========>..................] - ETA: 4s
4352/10000 [============>.................] - ETA: 4s
4448/10000 [============>.................] - ETA: 3s
4544/10000 [============>.................] - ETA: 3s
4640/10000 [============>.................] - ETA: 3s
4736/10000 [=============>................] - ETA: 3s
4832/10000 [=============>................] - ETA: 3s
4928/10000 [=============>................] - ETA: 3s
5024/10000 [==============>...............] - ETA: 3s
5120/10000 [==============>...............] - ETA: 3s
5216/10000 [==============>...............] - ETA: 3s
5344/10000 [===============>..............] - ETA: 3s
5408/10000 [===============>..............] - ETA: 3s
5504/10000 [===============>..............] - ETA: 3s
5600/10000 [===============>..............] - ETA: 3s
5696/10000 [================>.............] - ETA: 2s
5760/10000 [================>.............] - ETA: 2s
5856/10000 [================>.............] - ETA: 2s
5952/10000 [================>.............] - ETA: 2s
6048/10000 [=================>............] - ETA: 2s
6144/10000 [=================>............] - ETA: 2s
6240/10000 [=================>............] - ETA: 2s
6304/10000 [=================>............] - ETA: 2s
6400/10000 [==================>...........] - ETA: 2s
6496/10000 [==================>...........] - ETA: 2s
6592/10000 [==================>...........] - ETA: 2s
6688/10000 [===================>..........] - ETA: 2s
6784/10000 [===================>..........] - ETA: 2s
6848/10000 [===================>..........] - ETA: 2s
6944/10000 [===================>..........] - ETA: 2s
7008/10000 [====================>.........] - ETA: 2s
7072/10000 [====================>.........] - ETA: 2s
7168/10000 [====================>.........] - ETA: 1s
7264/10000 [====================>.........] - ETA: 1s
7360/10000 [=====================>........] - ETA: 1s
7456/10000 [=====================>........] - ETA: 1s
7552/10000 [=====================>........] - ETA: 1s
7648/10000 [=====================>........] - ETA: 1s
7744/10000 [======================>.......] - ETA: 1s
7840/10000 [======================>.......] - ETA: 1s
7936/10000 [======================>.......] - ETA: 1s
8032/10000 [=======================>......] - ETA: 1s
8128/10000 [=======================>......] - ETA: 1s
8224/10000 [=======================>......] - ETA: 1s
8320/10000 [=======================>......] - ETA: 1s
8416/10000 [========================>.....] - ETA: 1s
8512/10000 [========================>.....] - ETA: 1s
8576/10000 [========================>.....] - ETA: 0s
8672/10000 [=========================>....] - ETA: 0s
8768/10000 [=========================>....] - ETA: 0s
8864/10000 [=========================>....] - ETA: 0s
8960/10000 [=========================>....] - ETA: 0s
9056/10000 [==========================>...] - ETA: 0s
9152/10000 [==========================>...] - ETA: 0s
9248/10000 [==========================>...] - ETA: 0s
9344/10000 [===========================>..] - ETA: 0s
9440/10000 [===========================>..] - ETA: 0s
9536/10000 [===========================>..] - ETA: 0s
9632/10000 [===========================>..] - ETA: 0s
9728/10000 [============================>.] - ETA: 0s
9824/10000 [============================>.] - ETA: 0s
9920/10000 [============================>.] - ETA: 0s
9984/10000 [============================>.] - ETA: 0s
10000/10000 [==============================] - 7s 683us/step
loss: 0.046070
acc: 0.988900
Still Overfitting
We're making progress on our test error -- about 99% -- but just a bit for all the additional time, due to the network overfitting the data.
There are a variety of techniques we can take to counter this -- forms of regularization.
Let's try a relatively simple solution that works surprisingly well: add a pair of Dropout filters, a layer that randomly omits a fraction of neurons from each training batch (thus exposing each neuron to only part of the training data).
We'll add more convolution kernels but shrink them to 3x3 as well.
model = Sequential()
model.add(Conv2D(32, # number of kernels
(3, 3), # kernel size
padding='valid',
input_shape=(28, 28, 1)))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(rate=1-0.25)) #new parameter rate added (rate=1-keep_prob)
model.add(Flatten())
model.add(Dense(128))
model.add(Activation('relu'))
model.add(Dropout(rate=1-0.5)) #new parameter rate added (rate=1-keep_prob)
model.add(Dense(10))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(X_train, y_train, batch_size=128, epochs=15, verbose=2)
scores = model.evaluate(X_test, y_test, verbose=2)
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:3733: calling dropout (from tensorflow.python.ops.nn_ops) with keep_prob is deprecated and will be removed in a future version.
Instructions for updating:
Please use `rate` instead of `keep_prob`. Rate should be set to `rate = 1 - keep_prob`.
Epoch 1/15
- 339s - loss: 0.3906 - acc: 0.8762
Epoch 2/15
- 334s - loss: 0.1601 - acc: 0.9516
Epoch 3/15
- 271s - loss: 0.1282 - acc: 0.9610
Epoch 4/15
- 248s - loss: 0.1108 - acc: 0.9664
Epoch 5/15
- 245s - loss: 0.0972 - acc: 0.9705
Epoch 6/15
- 249s - loss: 0.0903 - acc: 0.9720
Epoch 7/15
- 245s - loss: 0.0859 - acc: 0.9737
Epoch 8/15
- 245s - loss: 0.0828 - acc: 0.9742
Epoch 9/15
- 249s - loss: 0.0786 - acc: 0.9756
Epoch 10/15
- 247s - loss: 0.0763 - acc: 0.9764
Epoch 11/15
- 247s - loss: 0.0752 - acc: 0.9765
Epoch 12/15
- 244s - loss: 0.0694 - acc: 0.9782
Epoch 13/15
- 247s - loss: 0.0693 - acc: 0.9786
Epoch 14/15
- 171s - loss: 0.0655 - acc: 0.9802
Epoch 15/15
- 157s - loss: 0.0647 - acc: 0.9801
loss: 0.023367
acc: 0.992200
Lab Wrapup
From the last lab, you should have a test accuracy of over 99.1%
For one more activity, try changing the optimizer to old-school "sgd" -- just to see how far we've come with these modern gradient descent techniques in the last few years.
Accuracy will end up noticeably worse ... about 96-97% test accuracy. Two key takeaways:
- Without a good optimizer, even a very powerful network design may not achieve results
- In fact, we could replace the word "optimizer" there with
- initialization
- activation
- regularization
- (etc.)
- All of these elements we've been working with operate together in a complex way to determine final performance
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
CIFAR 10
Details at: https://www.cs.toronto.edu/~kriz/cifar.html
Summary (taken from that page):
The CIFAR-10 and CIFAR-100 are labeled subsets of the 80 million tiny images dataset. They were collected by Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton. The CIFAR-10 dataset consists of 60000 32x32 colour images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images.
The dataset is divided into five training batches and one test batch, each with 10000 images. The test batch contains exactly 1000 randomly-selected images from each class. The training batches contain the remaining images in random order, but some training batches may contain more images from one class than another. Between them, the training batches contain exactly 5000 images from each class.
First, we'll mount the S3 bucket where I'm hosting the data:
# you may have to host the data yourself! - this should not work unless you can descramble
ACCESS="...SPORAA...KIAJZEH...PW46CWPUWUN...QPODO" # scrambled up
SECRET="...P7d7Sp7r1...Q9DuUvV...QAy1D+hjC...NxakJF+PXrAb...MXD1tZwBpGyN...1Ns5r5n1" # scrambled up
BUCKET = "cool-data"
MOUNT = "/mnt/cifar"
try:
dbutils.fs.mount("s3a://"+ ACCESS + ":" + SECRET + "@" + BUCKET, MOUNT)
except:
print("Error mounting ... possibly already mounted")
Error mounting ... possibly already mounted
This is in DBFS, which is available (via FUSE) at /dbfs ...
So the CIFAR data can be listed through following regular Linux shell command:
wget http://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
--2021-01-18 14:38:29-- http://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
Resolving www.cs.toronto.edu (www.cs.toronto.edu)... 128.100.3.30
Connecting to www.cs.toronto.edu (www.cs.toronto.edu)|128.100.3.30|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 170498071 (163M) [application/x-gzip]
Saving to: ‘cifar-10-python.tar.gz’
0K .......... .......... .......... .......... .......... 0% 340K 8m10s
50K .......... .......... .......... .......... .......... 0% 712K 6m2s
100K .......... .......... .......... .......... .......... 0% 677K 5m23s
150K .......... .......... .......... .......... .......... 0% 9.41M 4m6s
200K .......... .......... .......... .......... .......... 0% 727K 4m3s
250K .......... .......... .......... .......... .......... 0% 123M 3m23s
300K .......... .......... .......... .......... .......... 0% 33.2M 2m54s
350K .......... .......... .......... .......... .......... 0% 25.4M 2m33s
400K .......... .......... .......... .......... .......... 0% 723K 2m42s
450K .......... .......... .......... .......... .......... 0% 12.0M 2m27s
500K .......... .......... .......... .......... .......... 0% 9.97M 2m15s
550K .......... .......... .......... .......... .......... 0% 10.1M 2m5s
600K .......... .......... .......... .......... .......... 0% 13.8M 1m56s
650K .......... .......... .......... .......... .......... 0% 10.1M 1m49s
700K .......... .......... .......... .......... .......... 0% 1.01M 1m52s
750K .......... .......... .......... .......... .......... 0% 13.4M 1m46s
800K .......... .......... .......... .......... .......... 0% 13.0M 1m41s
850K .......... .......... .......... .......... .......... 0% 101M 95s
900K .......... .......... .......... .......... .......... 0% 25.4M 90s
950K .......... .......... .......... .......... .......... 0% 95.4M 86s
1000K .......... .......... .......... .......... .......... 0% 178M 82s
1050K .......... .......... .......... .......... .......... 0% 168M 78s
1100K .......... .......... .......... .......... .......... 0% 141M 75s
1150K .......... .......... .......... .......... .......... 0% 11.4M 72s
1200K .......... .......... .......... .......... .......... 0% 52.0M 69s
1250K .......... .......... .......... .......... .......... 0% 17.1M 67s
1300K .......... .......... .......... .......... .......... 0% 45.0M 65s
1350K .......... .......... .......... .......... .......... 0% 1.05M 68s
1400K .......... .......... .......... .......... .......... 0% 28.4M 66s
1450K .......... .......... .......... .......... .......... 0% 18.0M 64s
1500K .......... .......... .......... .......... .......... 0% 18.1M 62s
1550K .......... .......... .......... .......... .......... 0% 76.4M 60s
1600K .......... .......... .......... .......... .......... 0% 11.6M 59s
1650K .......... .......... .......... .......... .......... 1% 32.7M 57s
1700K .......... .......... .......... .......... .......... 1% 64.9M 56s
1750K .......... .......... .......... .......... .......... 1% 34.7M 54s
1800K .......... .......... .......... .......... .......... 1% 30.9M 53s
1850K .......... .......... .......... .......... .......... 1% 30.2M 51s
1900K .......... .......... .......... .......... .......... 1% 62.4M 50s
1950K .......... .......... .......... .......... .......... 1% 35.9M 49s
2000K .......... .......... .......... .......... .......... 1% 28.7M 48s
2050K .......... .......... .......... .......... .......... 1% 23.6M 47s
2100K .......... .......... .......... .......... .......... 1% 146M 46s
2150K .......... .......... .......... .......... .......... 1% 25.9M 45s
2200K .......... .......... .......... .......... .......... 1% 15.4M 44s
2250K .......... .......... .......... .......... .......... 1% 48.2M 43s
2300K .......... .......... .......... .......... .......... 1% 21.6M 43s
2350K .......... .......... .......... .......... .......... 1% 25.2M 42s
2400K .......... .......... .......... .......... .......... 1% 34.2M 41s
2450K .......... .......... .......... .......... .......... 1% 22.4M 40s
2500K .......... .......... .......... .......... .......... 1% 29.8M 40s
2550K .......... .......... .......... .......... .......... 1% 58.4M 39s
2600K .......... .......... .......... .......... .......... 1% 21.6M 38s
2650K .......... .......... .......... .......... .......... 1% 21.9M 38s
2700K .......... .......... .......... .......... .......... 1% 32.0M 37s
2750K .......... .......... .......... .......... .......... 1% 1.93M 38s
2800K .......... .......... .......... .......... .......... 1% 50.3M 37s
2850K .......... .......... .......... .......... .......... 1% 21.5M 37s
2900K .......... .......... .......... .......... .......... 1% 48.3M 36s
2950K .......... .......... .......... .......... .......... 1% 42.8M 36s
3000K .......... .......... .......... .......... .......... 1% 27.7M 35s
3050K .......... .......... .......... .......... .......... 1% 123M 35s
3100K .......... .......... .......... .......... .......... 1% 13.8M 34s
3150K .......... .......... .......... .......... .......... 1% 22.5M 34s
3200K .......... .......... .......... .......... .......... 1% 189M 33s
3250K .......... .......... .......... .......... .......... 1% 46.0M 33s
3300K .......... .......... .......... .......... .......... 2% 22.5M 32s
3350K .......... .......... .......... .......... .......... 2% 30.3M 32s
3400K .......... .......... .......... .......... .......... 2% 41.9M 32s
3450K .......... .......... .......... .......... .......... 2% 36.1M 31s
3500K .......... .......... .......... .......... .......... 2% 103M 31s
3550K .......... .......... .......... .......... .......... 2% 13.1M 30s
3600K .......... .......... .......... .......... .......... 2% 44.0M 30s
3650K .......... .......... .......... .......... .......... 2% 43.4M 30s
3700K .......... .......... .......... .......... .......... 2% 20.4M 29s
3750K .......... .......... .......... .......... .......... 2% 40.8M 29s
3800K .......... .......... .......... .......... .......... 2% 34.0M 29s
3850K .......... .......... .......... .......... .......... 2% 21.9M 28s
3900K .......... .......... .......... .......... .......... 2% 76.5M 28s
3950K .......... .......... .......... .......... .......... 2% 24.7M 28s
4000K .......... .......... .......... .......... .......... 2% 47.5M 28s
4050K .......... .......... .......... .......... .......... 2% 20.4M 27s
4100K .......... .......... .......... .......... .......... 2% 161M 27s
4150K .......... .......... .......... .......... .......... 2% 18.5M 27s
4200K .......... .......... .......... .......... .......... 2% 105M 26s
4250K .......... .......... .......... .......... .......... 2% 2.18M 27s
4300K .......... .......... .......... .......... .......... 2% 8.37M 27s
4350K .......... .......... .......... .......... .......... 2% 155M 27s
4400K .......... .......... .......... .......... .......... 2% 27.0M 26s
4450K .......... .......... .......... .......... .......... 2% 32.7M 26s
4500K .......... .......... .......... .......... .......... 2% 68.8M 26s
4550K .......... .......... .......... .......... .......... 2% 14.5M 26s
4600K .......... .......... .......... .......... .......... 2% 120M 25s
4650K .......... .......... .......... .......... .......... 2% 22.6M 25s
4700K .......... .......... .......... .......... .......... 2% 30.9M 25s
4750K .......... .......... .......... .......... .......... 2% 27.7M 25s
4800K .......... .......... .......... .......... .......... 2% 73.8M 24s
4850K .......... .......... .......... .......... .......... 2% 24.3M 24s
4900K .......... .......... .......... .......... .......... 2% 99.2M 24s
4950K .......... .......... .......... .......... .......... 3% 28.0M 24s
5000K .......... .......... .......... .......... .......... 3% 49.4M 24s
5050K .......... .......... .......... .......... .......... 3% 114M 23s
5100K .......... .......... .......... .......... .......... 3% 22.3M 23s
5150K .......... .......... .......... .......... .......... 3% 27.0M 23s
5200K .......... .......... .......... .......... .......... 3% 13.5M 23s
5250K .......... .......... .......... .......... .......... 3% 81.3M 23s
5300K .......... .......... .......... .......... .......... 3% 30.1M 23s
5350K .......... .......... .......... .......... .......... 3% 52.0M 22s
5400K .......... .......... .......... .......... .......... 3% 23.5M 22s
5450K .......... .......... .......... .......... .......... 3% 20.9M 22s
5500K .......... .......... .......... .......... .......... 3% 117M 22s
5550K .......... .......... .......... .......... .......... 3% 22.7M 22s
5600K .......... .......... .......... .......... .......... 3% 20.8M 22s
5650K .......... .......... .......... .......... .......... 3% 25.7M 22s
5700K .......... .......... .......... .......... .......... 3% 31.2M 21s
5750K .......... .......... .......... .......... .......... 3% 103M 21s
5800K .......... .......... .......... .......... .......... 3% 1.88M 22s
5850K .......... .......... .......... .......... .......... 3% 21.6M 22s
5900K .......... .......... .......... .......... .......... 3% 27.9M 21s
5950K .......... .......... .......... .......... .......... 3% 20.9M 21s
6000K .......... .......... .......... .......... .......... 3% 94.0M 21s
6050K .......... .......... .......... .......... .......... 3% 31.1M 21s
6100K .......... .......... .......... .......... .......... 3% 18.2M 21s
6150K .......... .......... .......... .......... .......... 3% 20.6M 21s
6200K .......... .......... .......... .......... .......... 3% 34.0M 21s
6250K .......... .......... .......... .......... .......... 3% 54.4M 20s
6300K .......... .......... .......... .......... .......... 3% 14.2M 20s
6350K .......... .......... .......... .......... .......... 3% 42.1M 20s
6400K .......... .......... .......... .......... .......... 3% 22.6M 20s
6450K .......... .......... .......... .......... .......... 3% 135M 20s
6500K .......... .......... .......... .......... .......... 3% 21.5M 20s
6550K .......... .......... .......... .......... .......... 3% 22.6M 20s
6600K .......... .......... .......... .......... .......... 3% 30.4M 20s
6650K .......... .......... .......... .......... .......... 4% 30.8M 20s
6700K .......... .......... .......... .......... .......... 4% 61.1M 19s
6750K .......... .......... .......... .......... .......... 4% 32.9M 19s
6800K .......... .......... .......... .......... .......... 4% 32.4M 19s
6850K .......... .......... .......... .......... .......... 4% 21.8M 19s
6900K .......... .......... .......... .......... .......... 4% 60.3M 19s
6950K .......... .......... .......... .......... .......... 4% 99.1M 19s
7000K .......... .......... .......... .......... .......... 4% 63.6M 19s
7050K .......... .......... .......... .......... .......... 4% 59.7M 19s
7100K .......... .......... .......... .......... .......... 4% 21.8M 19s
7150K .......... .......... .......... .......... .......... 4% 11.5M 19s
7200K .......... .......... .......... .......... .......... 4% 103M 18s
7250K .......... .......... .......... .......... .......... 4% 155M 18s
7300K .......... .......... .......... .......... .......... 4% 2.34M 19s
7350K .......... .......... .......... .......... .......... 4% 9.40M 19s
7400K .......... .......... .......... .......... .......... 4% 88.7M 18s
7450K .......... .......... .......... .......... .......... 4% 14.5M 18s
7500K .......... .......... .......... .......... .......... 4% 82.8M 18s
7550K .......... .......... .......... .......... .......... 4% 38.5M 18s
7600K .......... .......... .......... .......... .......... 4% 71.5M 18s
7650K .......... .......... .......... .......... .......... 4% 16.4M 18s
7700K .......... .......... .......... .......... .......... 4% 15.8M 18s
7750K .......... .......... .......... .......... .......... 4% 91.1M 18s
7800K .......... .......... .......... .......... .......... 4% 13.1M 18s
7850K .......... .......... .......... .......... .......... 4% 87.1M 18s
7900K .......... .......... .......... .......... .......... 4% 50.4M 18s
7950K .......... .......... .......... .......... .......... 4% 21.3M 18s
8000K .......... .......... .......... .......... .......... 4% 23.4M 17s
8050K .......... .......... .......... .......... .......... 4% 22.5M 17s
8100K .......... .......... .......... .......... .......... 4% 42.8M 17s
8150K .......... .......... .......... .......... .......... 4% 47.4M 17s
8200K .......... .......... .......... .......... .......... 4% 26.0M 17s
8250K .......... .......... .......... .......... .......... 4% 36.7M 17s
8300K .......... .......... .......... .......... .......... 5% 101M 17s
8350K .......... .......... .......... .......... .......... 5% 16.6M 17s
8400K .......... .......... .......... .......... .......... 5% 81.7M 17s
8450K .......... .......... .......... .......... .......... 5% 65.8M 17s
8500K .......... .......... .......... .......... .......... 5% 44.3M 17s
8550K .......... .......... .......... .......... .......... 5% 133M 17s
8600K .......... .......... .......... .......... .......... 5% 50.0M 16s
8650K .......... .......... .......... .......... .......... 5% 19.4M 16s
8700K .......... .......... .......... .......... .......... 5% 27.6M 16s
8750K .......... .......... .......... .......... .......... 5% 20.4M 16s
8800K .......... .......... .......... .......... .......... 5% 79.5M 16s
8850K .......... .......... .......... .......... .......... 5% 2.03M 17s
8900K .......... .......... .......... .......... .......... 5% 17.4M 16s
8950K .......... .......... .......... .......... .......... 5% 12.0M 16s
9000K .......... .......... .......... .......... .......... 5% 83.2M 16s
9050K .......... .......... .......... .......... .......... 5% 51.4M 16s
9100K .......... .......... .......... .......... .......... 5% 51.7M 16s
9150K .......... .......... .......... .......... .......... 5% 17.2M 16s
9200K .......... .......... .......... .......... .......... 5% 30.0M 16s
9250K .......... .......... .......... .......... .......... 5% 60.3M 16s
9300K .......... .......... .......... .......... .......... 5% 48.9M 16s
9350K .......... .......... .......... .......... .......... 5% 13.0M 16s
9400K .......... .......... .......... .......... .......... 5% 23.0M 16s
9450K .......... .......... .......... .......... .......... 5% 31.2M 16s
9500K .......... .......... .......... .......... .......... 5% 85.2M 16s
9550K .......... .......... .......... .......... .......... 5% 24.7M 16s
9600K .......... .......... .......... .......... .......... 5% 20.9M 16s
9650K .......... .......... .......... .......... .......... 5% 23.1M 16s
9700K .......... .......... .......... .......... .......... 5% 59.1M 15s
9750K .......... .......... .......... .......... .......... 5% 27.9M 15s
9800K .......... .......... .......... .......... .......... 5% 14.5M 15s
9850K .......... .......... .......... .......... .......... 5% 72.8M 15s
9900K .......... .......... .......... .......... .......... 5% 26.2M 15s
9950K .......... .......... .......... .......... .......... 6% 97.1M 15s
10000K .......... .......... .......... .......... .......... 6% 13.8M 15s
10050K .......... .......... .......... .......... .......... 6% 54.0M 15s
10100K .......... .......... .......... .......... .......... 6% 33.4M 15s
10150K .......... .......... .......... .......... .......... 6% 23.1M 15s
10200K .......... .......... .......... .......... .......... 6% 43.3M 15s
10250K .......... .......... .......... .......... .......... 6% 21.2M 15s
10300K .......... .......... .......... .......... .......... 6% 26.7M 15s
10350K .......... .......... .......... .......... .......... 6% 3.01M 15s
10400K .......... .......... .......... .......... .......... 6% 19.5M 15s
10450K .......... .......... .......... .......... .......... 6% 11.5M 15s
10500K .......... .......... .......... .......... .......... 6% 14.7M 15s
10550K .......... .......... .......... .......... .......... 6% 24.1M 15s
10600K .......... .......... .......... .......... .......... 6% 31.5M 15s
10650K .......... .......... .......... .......... .......... 6% 111M 15s
10700K .......... .......... .......... .......... .......... 6% 24.4M 15s
10750K .......... .......... .......... .......... .......... 6% 29.9M 15s
10800K .......... .......... .......... .......... .......... 6% 45.4M 15s
10850K .......... .......... .......... .......... .......... 6% 11.4M 15s
10900K .......... .......... .......... .......... .......... 6% 47.3M 15s
10950K .......... .......... .......... .......... .......... 6% 49.5M 14s
11000K .......... .......... .......... .......... .......... 6% 23.1M 14s
11050K .......... .......... .......... .......... .......... 6% 29.2M 14s
11100K .......... .......... .......... .......... .......... 6% 67.0M 14s
11150K .......... .......... .......... .......... .......... 6% 24.0M 14s
11200K .......... .......... .......... .......... .......... 6% 22.9M 14s
11250K .......... .......... .......... .......... .......... 6% 33.2M 14s
11300K .......... .......... .......... .......... .......... 6% 29.7M 14s
11350K .......... .......... .......... .......... .......... 6% 26.2M 14s
11400K .......... .......... .......... .......... .......... 6% 109M 14s
11450K .......... .......... .......... .......... .......... 6% 32.4M 14s
11500K .......... .......... .......... .......... .......... 6% 12.9M 14s
11550K .......... .......... .......... .......... .......... 6% 59.2M 14s
11600K .......... .......... .......... .......... .......... 6% 71.9M 14s
11650K .......... .......... .......... .......... .......... 7% 40.7M 14s
11700K .......... .......... .......... .......... .......... 7% 21.6M 14s
11750K .......... .......... .......... .......... .......... 7% 23.9M 14s
11800K .......... .......... .......... .......... .......... 7% 28.7M 14s
11850K .......... .......... .......... .......... .......... 7% 24.0M 14s
11900K .......... .......... .......... .......... .......... 7% 2.81M 14s
11950K .......... .......... .......... .......... .......... 7% 12.3M 14s
12000K .......... .......... .......... .......... .......... 7% 16.6M 14s
12050K .......... .......... .......... .......... .......... 7% 28.9M 14s
12100K .......... .......... .......... .......... .......... 7% 23.6M 14s
12150K .......... .......... .......... .......... .......... 7% 46.2M 14s
12200K .......... .......... .......... .......... .......... 7% 20.0M 14s
12250K .......... .......... .......... .......... .......... 7% 48.5M 14s
12300K .......... .......... .......... .......... .......... 7% 70.2M 14s
12350K .......... .......... .......... .......... .......... 7% 43.2M 14s
12400K .......... .......... .......... .......... .......... 7% 10.2M 14s
12450K .......... .......... .......... .......... .......... 7% 45.6M 14s
12500K .......... .......... .......... .......... .......... 7% 112M 13s
12550K .......... .......... .......... .......... .......... 7% 15.1M 13s
12600K .......... .......... .......... .......... .......... 7% 30.3M 13s
12650K .......... .......... .......... .......... .......... 7% 19.0M 13s
12700K .......... .......... .......... .......... .......... 7% 30.7M 13s
12750K .......... .......... .......... .......... .......... 7% 73.2M 13s
12800K .......... .......... .......... .......... .......... 7% 20.8M 13s
12850K .......... .......... .......... .......... .......... 7% 34.2M 13s
12900K .......... .......... .......... .......... .......... 7% 30.2M 13s
12950K .......... .......... .......... .......... .......... 7% 33.7M 13s
13000K .......... .......... .......... .......... .......... 7% 66.8M 13s
13050K .......... .......... .......... .......... .......... 7% 13.1M 13s
13100K .......... .......... .......... .......... .......... 7% 56.5M 13s
13150K .......... .......... .......... .......... .......... 7% 53.4M 13s
13200K .......... .......... .......... .......... .......... 7% 126M 13s
13250K .......... .......... .......... .......... .......... 7% 28.1M 13s
13300K .......... .......... .......... .......... .......... 8% 16.7M 13s
13350K .......... .......... .......... .......... .......... 8% 23.8M 13s
13400K .......... .......... .......... .......... .......... 8% 3.20M 13s
13450K .......... .......... .......... .......... .......... 8% 13.0M 13s
13500K .......... .......... .......... .......... .......... 8% 10.5M 13s
13550K .......... .......... .......... .......... .......... 8% 24.9M 13s
13600K .......... .......... .......... .......... .......... 8% 49.6M 13s
13650K .......... .......... .......... .......... .......... 8% 14.6M 13s
13700K .......... .......... .......... .......... .......... 8% 148M 13s
13750K .......... .......... .......... .......... .......... 8% 15.5M 13s
13800K .......... .......... .......... .......... .......... 8% 21.3M 13s
13850K .......... .......... .......... .......... .......... 8% 6.80M 13s
13900K .......... .......... .......... .......... .......... 8% 115M 13s
13950K .......... .......... .......... .......... .......... 8% 78.6M 13s
14000K .......... .......... .......... .......... .......... 8% 73.9M 13s
14050K .......... .......... .......... .......... .......... 8% 64.7M 13s
14100K .......... .......... .......... .......... .......... 8% 39.2M 13s
14150K .......... .......... .......... .......... .......... 8% 60.3M 13s
14200K .......... .......... .......... .......... .......... 8% 34.7M 13s
14250K .......... .......... .......... .......... .......... 8% 38.8M 13s
14300K .......... .......... .......... .......... .......... 8% 15.7M 13s
14350K .......... .......... .......... .......... .......... 8% 32.6M 12s
14400K .......... .......... .......... .......... .......... 8% 45.4M 12s
14450K .......... .......... .......... .......... .......... 8% 28.2M 12s
14500K .......... .......... .......... .......... .......... 8% 47.0M 12s
14550K .......... .......... .......... .......... .......... 8% 48.2M 12s
14600K .......... .......... .......... .......... .......... 8% 16.8M 12s
14650K .......... .......... .......... .......... .......... 8% 40.9M 12s
14700K .......... .......... .......... .......... .......... 8% 33.6M 12s
14750K .......... .......... .......... .......... .......... 8% 21.8M 12s
14800K .......... .......... .......... .......... .......... 8% 21.1M 12s
14850K .......... .......... .......... .......... .......... 8% 81.7M 12s
14900K .......... .......... .......... .......... .......... 8% 19.4M 12s
14950K .......... .......... .......... .......... .......... 9% 2.91M 12s
15000K .......... .......... .......... .......... .......... 9% 95.3M 12s
15050K .......... .......... .......... .......... .......... 9% 4.33M 12s
15100K .......... .......... .......... .......... .......... 9% 166M 12s
15150K .......... .......... .......... .......... .......... 9% 138M 12s
15200K .......... .......... .......... .......... .......... 9% 164M 12s
15250K .......... .......... .......... .......... .......... 9% 63.8M 12s
15300K .......... .......... .......... .......... .......... 9% 49.4M 12s
15350K .......... .......... .......... .......... .......... 9% 20.9M 12s
15400K .......... .......... .......... .......... .......... 9% 17.4M 12s
15450K .......... .......... .......... .......... .......... 9% 24.1M 12s
15500K .......... .......... .......... .......... .......... 9% 50.1M 12s
15550K .......... .......... .......... .......... .......... 9% 31.5M 12s
15600K .......... .......... .......... .......... .......... 9% 14.7M 12s
15650K .......... .......... .......... .......... .......... 9% 78.0M 12s
15700K .......... .......... .......... .......... .......... 9% 48.0M 12s
15750K .......... .......... .......... .......... .......... 9% 27.1M 12s
15800K .......... .......... .......... .......... .......... 9% 41.9M 12s
15850K .......... .......... .......... .......... .......... 9% 22.0M 12s
15900K .......... .......... .......... .......... .......... 9% 18.9M 12s
15950K .......... .......... .......... .......... .......... 9% 33.0M 12s
*** WARNING: skipped 204162 bytes of output ***
150200K .......... .......... .......... .......... .......... 90% 22.1M 1s
150250K .......... .......... .......... .......... .......... 90% 19.7M 1s
150300K .......... .......... .......... .......... .......... 90% 20.7M 1s
150350K .......... .......... .......... .......... .......... 90% 18.6M 1s
150400K .......... .......... .......... .......... .......... 90% 19.5M 1s
150450K .......... .......... .......... .......... .......... 90% 46.1M 1s
150500K .......... .......... .......... .......... .......... 90% 19.1M 1s
150550K .......... .......... .......... .......... .......... 90% 12.4M 1s
150600K .......... .......... .......... .......... .......... 90% 16.3M 1s
150650K .......... .......... .......... .......... .......... 90% 122M 1s
150700K .......... .......... .......... .......... .......... 90% 16.8M 1s
150750K .......... .......... .......... .......... .......... 90% 47.7M 1s
150800K .......... .......... .......... .......... .......... 90% 44.2M 1s
150850K .......... .......... .......... .......... .......... 90% 21.8M 1s
150900K .......... .......... .......... .......... .......... 90% 73.6M 1s
150950K .......... .......... .......... .......... .......... 90% 18.4M 1s
151000K .......... .......... .......... .......... .......... 90% 12.4M 1s
151050K .......... .......... .......... .......... .......... 90% 18.7M 1s
151100K .......... .......... .......... .......... .......... 90% 12.7M 1s
151150K .......... .......... .......... .......... .......... 90% 23.4M 1s
151200K .......... .......... .......... .......... .......... 90% 12.2M 1s
151250K .......... .......... .......... .......... .......... 90% 16.0M 1s
151300K .......... .......... .......... .......... .......... 90% 19.5M 1s
151350K .......... .......... .......... .......... .......... 90% 64.8M 1s
151400K .......... .......... .......... .......... .......... 90% 15.9M 1s
151450K .......... .......... .......... .......... .......... 90% 37.7M 1s
151500K .......... .......... .......... .......... .......... 91% 23.2M 1s
151550K .......... .......... .......... .......... .......... 91% 13.7M 1s
151600K .......... .......... .......... .......... .......... 91% 24.5M 1s
151650K .......... .......... .......... .......... .......... 91% 20.1M 1s
151700K .......... .......... .......... .......... .......... 91% 30.8M 1s
151750K .......... .......... .......... .......... .......... 91% 18.0M 1s
151800K .......... .......... .......... .......... .......... 91% 26.8M 1s
151850K .......... .......... .......... .......... .......... 91% 78.1M 1s
151900K .......... .......... .......... .......... .......... 91% 18.2M 1s
151950K .......... .......... .......... .......... .......... 91% 14.7M 1s
152000K .......... .......... .......... .......... .......... 91% 119M 1s
152050K .......... .......... .......... .......... .......... 91% 19.9M 1s
152100K .......... .......... .......... .......... .......... 91% 11.7M 1s
152150K .......... .......... .......... .......... .......... 91% 17.9M 1s
152200K .......... .......... .......... .......... .......... 91% 13.1M 1s
152250K .......... .......... .......... .......... .......... 91% 33.8M 1s
152300K .......... .......... .......... .......... .......... 91% 106M 1s
152350K .......... .......... .......... .......... .......... 91% 43.1M 1s
152400K .......... .......... .......... .......... .......... 91% 24.5M 1s
152450K .......... .......... .......... .......... .......... 91% 18.5M 1s
152500K .......... .......... .......... .......... .......... 91% 12.4M 1s
152550K .......... .......... .......... .......... .......... 91% 104M 1s
152600K .......... .......... .......... .......... .......... 91% 22.3M 1s
152650K .......... .......... .......... .......... .......... 91% 8.15M 1s
152700K .......... .......... .......... .......... .......... 91% 14.8M 1s
152750K .......... .......... .......... .......... .......... 91% 47.3M 1s
152800K .......... .......... .......... .......... .......... 91% 16.7M 1s
152850K .......... .......... .......... .......... .......... 91% 26.9M 1s
152900K .......... .......... .......... .......... .......... 91% 16.6M 1s
152950K .......... .......... .......... .......... .......... 91% 25.4M 1s
153000K .......... .......... .......... .......... .......... 91% 53.0M 1s
153050K .......... .......... .......... .......... .......... 91% 46.3M 1s
153100K .......... .......... .......... .......... .......... 91% 8.79M 1s
153150K .......... .......... .......... .......... .......... 92% 20.4M 1s
153200K .......... .......... .......... .......... .......... 92% 34.2M 1s
153250K .......... .......... .......... .......... .......... 92% 89.4M 1s
153300K .......... .......... .......... .......... .......... 92% 17.4M 1s
153350K .......... .......... .......... .......... .......... 92% 27.5M 1s
153400K .......... .......... .......... .......... .......... 92% 15.6M 1s
153450K .......... .......... .......... .......... .......... 92% 88.0M 1s
153500K .......... .......... .......... .......... .......... 92% 14.8M 1s
153550K .......... .......... .......... .......... .......... 92% 22.4M 1s
153600K .......... .......... .......... .......... .......... 92% 13.7M 1s
153650K .......... .......... .......... .......... .......... 92% 15.1M 1s
153700K .......... .......... .......... .......... .......... 92% 91.5M 1s
153750K .......... .......... .......... .......... .......... 92% 13.6M 1s
153800K .......... .......... .......... .......... .......... 92% 27.9M 1s
153850K .......... .......... .......... .......... .......... 92% 55.8M 1s
153900K .......... .......... .......... .......... .......... 92% 32.6M 1s
153950K .......... .......... .......... .......... .......... 92% 59.6M 1s
154000K .......... .......... .......... .......... .......... 92% 16.3M 1s
154050K .......... .......... .......... .......... .......... 92% 7.24M 1s
154100K .......... .......... .......... .......... .......... 92% 102M 1s
154150K .......... .......... .......... .......... .......... 92% 114M 1s
154200K .......... .......... .......... .......... .......... 92% 9.56M 1s
154250K .......... .......... .......... .......... .......... 92% 9.85M 1s
154300K .......... .......... .......... .......... .......... 92% 23.1M 1s
154350K .......... .......... .......... .......... .......... 92% 63.5M 1s
154400K .......... .......... .......... .......... .......... 92% 62.1M 1s
154450K .......... .......... .......... .......... .......... 92% 15.5M 1s
154500K .......... .......... .......... .......... .......... 92% 21.2M 1s
154550K .......... .......... .......... .......... .......... 92% 46.8M 1s
154600K .......... .......... .......... .......... .......... 92% 8.33M 1s
154650K .......... .......... .......... .......... .......... 92% 77.7M 1s
154700K .......... .......... .......... .......... .......... 92% 24.6M 1s
154750K .......... .......... .......... .......... .......... 92% 35.6M 1s
154800K .......... .......... .......... .......... .......... 93% 20.2M 1s
154850K .......... .......... .......... .......... .......... 93% 61.5M 1s
154900K .......... .......... .......... .......... .......... 93% 23.9M 1s
154950K .......... .......... .......... .......... .......... 93% 15.1M 1s
155000K .......... .......... .......... .......... .......... 93% 16.9M 1s
155050K .......... .......... .......... .......... .......... 93% 21.0M 1s
155100K .......... .......... .......... .......... .......... 93% 135M 1s
155150K .......... .......... .......... .......... .......... 93% 11.1M 1s
155200K .......... .......... .......... .......... .......... 93% 17.3M 1s
155250K .......... .......... .......... .......... .......... 93% 14.6M 1s
155300K .......... .......... .......... .......... .......... 93% 35.1M 1s
155350K .......... .......... .......... .......... .......... 93% 35.9M 1s
155400K .......... .......... .......... .......... .......... 93% 51.8M 1s
155450K .......... .......... .......... .......... .......... 93% 27.8M 1s
155500K .......... .......... .......... .......... .......... 93% 20.5M 1s
155550K .......... .......... .......... .......... .......... 93% 56.7M 1s
155600K .......... .......... .......... .......... .......... 93% 13.0M 1s
155650K .......... .......... .......... .......... .......... 93% 24.2M 1s
155700K .......... .......... .......... .......... .......... 93% 14.8M 1s
155750K .......... .......... .......... .......... .......... 93% 7.81M 1s
155800K .......... .......... .......... .......... .......... 93% 64.4M 1s
155850K .......... .......... .......... .......... .......... 93% 13.4M 1s
155900K .......... .......... .......... .......... .......... 93% 19.7M 1s
155950K .......... .......... .......... .......... .......... 93% 19.6M 1s
156000K .......... .......... .......... .......... .......... 93% 30.1M 1s
156050K .......... .......... .......... .......... .......... 93% 50.1M 1s
156100K .......... .......... .......... .......... .......... 93% 27.8M 1s
156150K .......... .......... .......... .......... .......... 93% 10.5M 1s
156200K .......... .......... .......... .......... .......... 93% 18.4M 1s
156250K .......... .......... .......... .......... .......... 93% 95.9M 1s
156300K .......... .......... .......... .......... .......... 93% 22.7M 1s
156350K .......... .......... .......... .......... .......... 93% 22.8M 1s
156400K .......... .......... .......... .......... .......... 93% 22.0M 1s
156450K .......... .......... .......... .......... .......... 93% 20.8M 0s
156500K .......... .......... .......... .......... .......... 94% 62.2M 0s
156550K .......... .......... .......... .......... .......... 94% 16.5M 0s
156600K .......... .......... .......... .......... .......... 94% 23.0M 0s
156650K .......... .......... .......... .......... .......... 94% 16.9M 0s
156700K .......... .......... .......... .......... .......... 94% 14.9M 0s
156750K .......... .......... .......... .......... .......... 94% 99.6M 0s
156800K .......... .......... .......... .......... .......... 94% 11.9M 0s
156850K .......... .......... .......... .......... .......... 94% 30.2M 0s
156900K .......... .......... .......... .......... .......... 94% 22.3M 0s
156950K .......... .......... .......... .......... .......... 94% 92.4M 0s
157000K .......... .......... .......... .......... .......... 94% 58.2M 0s
157050K .......... .......... .......... .......... .......... 94% 17.7M 0s
157100K .......... .......... .......... .......... .......... 94% 7.60M 0s
157150K .......... .......... .......... .......... .......... 94% 99.6M 0s
157200K .......... .......... .......... .......... .......... 94% 174M 0s
157250K .......... .......... .......... .......... .......... 94% 10.8M 0s
157300K .......... .......... .......... .......... .......... 94% 10.9M 0s
157350K .......... .......... .......... .......... .......... 94% 12.1M 0s
157400K .......... .......... .......... .......... .......... 94% 21.7M 0s
157450K .......... .......... .......... .......... .......... 94% 107M 0s
157500K .......... .......... .......... .......... .......... 94% 20.5M 0s
157550K .......... .......... .......... .......... .......... 94% 24.6M 0s
157600K .......... .......... .......... .......... .......... 94% 20.8M 0s
157650K .......... .......... .......... .......... .......... 94% 60.3M 0s
157700K .......... .......... .......... .......... .......... 94% 13.0M 0s
157750K .......... .......... .......... .......... .......... 94% 19.2M 0s
157800K .......... .......... .......... .......... .......... 94% 21.7M 0s
157850K .......... .......... .......... .......... .......... 94% 19.5M 0s
157900K .......... .......... .......... .......... .......... 94% 60.4M 0s
157950K .......... .......... .......... .......... .......... 94% 19.3M 0s
158000K .......... .......... .......... .......... .......... 94% 25.5M 0s
158050K .......... .......... .......... .......... .......... 94% 16.8M 0s
158100K .......... .......... .......... .......... .......... 94% 28.7M 0s
158150K .......... .......... .......... .......... .......... 95% 55.7M 0s
158200K .......... .......... .......... .......... .......... 95% 15.0M 0s
158250K .......... .......... .......... .......... .......... 95% 16.3M 0s
158300K .......... .......... .......... .......... .......... 95% 56.1M 0s
158350K .......... .......... .......... .......... .......... 95% 9.03M 0s
158400K .......... .......... .......... .......... .......... 95% 130M 0s
158450K .......... .......... .......... .......... .......... 95% 31.4M 0s
158500K .......... .......... .......... .......... .......... 95% 53.9M 0s
158550K .......... .......... .......... .......... .......... 95% 15.8M 0s
158600K .......... .......... .......... .......... .......... 95% 165M 0s
158650K .......... .......... .......... .......... .......... 95% 11.3M 0s
158700K .......... .......... .......... .......... .......... 95% 27.8M 0s
158750K .......... .......... .......... .......... .......... 95% 21.9M 0s
158800K .......... .......... .......... .......... .......... 95% 7.42M 0s
158850K .......... .......... .......... .......... .......... 95% 55.6M 0s
158900K .......... .......... .......... .......... .......... 95% 11.7M 0s
158950K .......... .......... .......... .......... .......... 95% 20.0M 0s
159000K .......... .......... .......... .......... .......... 95% 23.1M 0s
159050K .......... .......... .......... .......... .......... 95% 55.3M 0s
159100K .......... .......... .......... .......... .......... 95% 27.0M 0s
159150K .......... .......... .......... .......... .......... 95% 18.9M 0s
159200K .......... .......... .......... .......... .......... 95% 14.1M 0s
159250K .......... .......... .......... .......... .......... 95% 17.9M 0s
159300K .......... .......... .......... .......... .......... 95% 94.0M 0s
159350K .......... .......... .......... .......... .......... 95% 18.8M 0s
159400K .......... .......... .......... .......... .......... 95% 22.0M 0s
159450K .......... .......... .......... .......... .......... 95% 24.5M 0s
159500K .......... .......... .......... .......... .......... 95% 19.1M 0s
159550K .......... .......... .......... .......... .......... 95% 65.9M 0s
159600K .......... .......... .......... .......... .......... 95% 11.8M 0s
159650K .......... .......... .......... .......... .......... 95% 25.2M 0s
159700K .......... .......... .......... .......... .......... 95% 15.3M 0s
159750K .......... .......... .......... .......... .......... 95% 76.7M 0s
159800K .......... .......... .......... .......... .......... 96% 15.6M 0s
159850K .......... .......... .......... .......... .......... 96% 11.4M 0s
159900K .......... .......... .......... .......... .......... 96% 95.4M 0s
159950K .......... .......... .......... .......... .......... 96% 16.4M 0s
160000K .......... .......... .......... .......... .......... 96% 65.6M 0s
160050K .......... .......... .......... .......... .......... 96% 41.2M 0s
160100K .......... .......... .......... .......... .......... 96% 21.1M 0s
160150K .......... .......... .......... .......... .......... 96% 15.5M 0s
160200K .......... .......... .......... .......... .......... 96% 21.6M 0s
160250K .......... .......... .......... .......... .......... 96% 41.7M 0s
160300K .......... .......... .......... .......... .......... 96% 12.8M 0s
160350K .......... .......... .......... .......... .......... 96% 13.5M 0s
160400K .......... .......... .......... .......... .......... 96% 11.5M 0s
160450K .......... .......... .......... .......... .......... 96% 65.7M 0s
160500K .......... .......... .......... .......... .......... 96% 19.1M 0s
160550K .......... .......... .......... .......... .......... 96% 19.5M 0s
160600K .......... .......... .......... .......... .......... 96% 26.1M 0s
160650K .......... .......... .......... .......... .......... 96% 19.5M 0s
160700K .......... .......... .......... .......... .......... 96% 85.4M 0s
160750K .......... .......... .......... .......... .......... 96% 14.8M 0s
160800K .......... .......... .......... .......... .......... 96% 16.2M 0s
160850K .......... .......... .......... .......... .......... 96% 27.5M 0s
160900K .......... .......... .......... .......... .......... 96% 13.6M 0s
160950K .......... .......... .......... .......... .......... 96% 94.8M 0s
161000K .......... .......... .......... .......... .......... 96% 17.6M 0s
161050K .......... .......... .......... .......... .......... 96% 20.0M 0s
161100K .......... .......... .......... .......... .......... 96% 24.3M 0s
161150K .......... .......... .......... .......... .......... 96% 31.8M 0s
161200K .......... .......... .......... .......... .......... 96% 19.8M 0s
161250K .......... .......... .......... .......... .......... 96% 19.6M 0s
161300K .......... .......... .......... .......... .......... 96% 18.7M 0s
161350K .......... .......... .......... .......... .......... 96% 12.4M 0s
161400K .......... .......... .......... .......... .......... 96% 21.7M 0s
161450K .......... .......... .......... .......... .......... 96% 28.8M 0s
161500K .......... .......... .......... .......... .......... 97% 20.6M 0s
161550K .......... .......... .......... .......... .......... 97% 28.5M 0s
161600K .......... .......... .......... .......... .......... 97% 18.5M 0s
161650K .......... .......... .......... .......... .......... 97% 89.5M 0s
161700K .......... .......... .......... .......... .......... 97% 13.2M 0s
161750K .......... .......... .......... .......... .......... 97% 58.5M 0s
161800K .......... .......... .......... .......... .......... 97% 12.4M 0s
161850K .......... .......... .......... .......... .......... 97% 16.3M 0s
161900K .......... .......... .......... .......... .......... 97% 35.4M 0s
161950K .......... .......... .......... .......... .......... 97% 9.31M 0s
162000K .......... .......... .......... .......... .......... 97% 14.8M 0s
162050K .......... .......... .......... .......... .......... 97% 32.5M 0s
162100K .......... .......... .......... .......... .......... 97% 41.4M 0s
162150K .......... .......... .......... .......... .......... 97% 21.4M 0s
162200K .......... .......... .......... .......... .......... 97% 38.4M 0s
162250K .......... .......... .......... .......... .......... 97% 14.5M 0s
162300K .......... .......... .......... .......... .......... 97% 10.7M 0s
162350K .......... .......... .......... .......... .......... 97% 32.5M 0s
162400K .......... .......... .......... .......... .......... 97% 48.7M 0s
162450K .......... .......... .......... .......... .......... 97% 15.6M 0s
162500K .......... .......... .......... .......... .......... 97% 23.8M 0s
162550K .......... .......... .......... .......... .......... 97% 32.3M 0s
162600K .......... .......... .......... .......... .......... 97% 29.4M 0s
162650K .......... .......... .......... .......... .......... 97% 16.8M 0s
162700K .......... .......... .......... .......... .......... 97% 26.7M 0s
162750K .......... .......... .......... .......... .......... 97% 17.8M 0s
162800K .......... .......... .......... .......... .......... 97% 63.2M 0s
162850K .......... .......... .......... .......... .......... 97% 15.8M 0s
162900K .......... .......... .......... .......... .......... 97% 15.9M 0s
162950K .......... .......... .......... .......... .......... 97% 12.5M 0s
163000K .......... .......... .......... .......... .......... 97% 24.2M 0s
163050K .......... .......... .......... .......... .......... 97% 50.5M 0s
163100K .......... .......... .......... .......... .......... 97% 24.5M 0s
163150K .......... .......... .......... .......... .......... 98% 27.2M 0s
163200K .......... .......... .......... .......... .......... 98% 22.4M 0s
163250K .......... .......... .......... .......... .......... 98% 11.0M 0s
163300K .......... .......... .......... .......... .......... 98% 72.7M 0s
163350K .......... .......... .......... .......... .......... 98% 18.7M 0s
163400K .......... .......... .......... .......... .......... 98% 14.4M 0s
163450K .......... .......... .......... .......... .......... 98% 11.6M 0s
163500K .......... .......... .......... .......... .......... 98% 29.2M 0s
163550K .......... .......... .......... .......... .......... 98% 14.4M 0s
163600K .......... .......... .......... .......... .......... 98% 25.7M 0s
163650K .......... .......... .......... .......... .......... 98% 25.8M 0s
163700K .......... .......... .......... .......... .......... 98% 26.6M 0s
163750K .......... .......... .......... .......... .......... 98% 97.2M 0s
163800K .......... .......... .......... .......... .......... 98% 13.0M 0s
163850K .......... .......... .......... .......... .......... 98% 10.8M 0s
163900K .......... .......... .......... .......... .......... 98% 31.2M 0s
163950K .......... .......... .......... .......... .......... 98% 18.8M 0s
164000K .......... .......... .......... .......... .......... 98% 31.9M 0s
164050K .......... .......... .......... .......... .......... 98% 22.9M 0s
164100K .......... .......... .......... .......... .......... 98% 28.9M 0s
164150K .......... .......... .......... .......... .......... 98% 18.3M 0s
164200K .......... .......... .......... .......... .......... 98% 79.7M 0s
164250K .......... .......... .......... .......... .......... 98% 19.7M 0s
164300K .......... .......... .......... .......... .......... 98% 18.0M 0s
164350K .......... .......... .......... .......... .......... 98% 17.4M 0s
164400K .......... .......... .......... .......... .......... 98% 9.15M 0s
164450K .......... .......... .......... .......... .......... 98% 122M 0s
164500K .......... .......... .......... .......... .......... 98% 20.5M 0s
164550K .......... .......... .......... .......... .......... 98% 21.8M 0s
164600K .......... .......... .......... .......... .......... 98% 25.9M 0s
164650K .......... .......... .......... .......... .......... 98% 21.8M 0s
164700K .......... .......... .......... .......... .......... 98% 80.9M 0s
164750K .......... .......... .......... .......... .......... 98% 7.10M 0s
164800K .......... .......... .......... .......... .......... 99% 117M 0s
164850K .......... .......... .......... .......... .......... 99% 36.1M 0s
164900K .......... .......... .......... .......... .......... 99% 52.0M 0s
164950K .......... .......... .......... .......... .......... 99% 13.7M 0s
165000K .......... .......... .......... .......... .......... 99% 9.19M 0s
165050K .......... .......... .......... .......... .......... 99% 23.1M 0s
165100K .......... .......... .......... .......... .......... 99% 13.2M 0s
165150K .......... .......... .......... .......... .......... 99% 77.8M 0s
165200K .......... .......... .......... .......... .......... 99% 29.2M 0s
165250K .......... .......... .......... .......... .......... 99% 23.6M 0s
165300K .......... .......... .......... .......... .......... 99% 26.8M 0s
165350K .......... .......... .......... .......... .......... 99% 11.2M 0s
165400K .......... .......... .......... .......... .......... 99% 31.1M 0s
165450K .......... .......... .......... .......... .......... 99% 21.1M 0s
165500K .......... .......... .......... .......... .......... 99% 23.9M 0s
165550K .......... .......... .......... .......... .......... 99% 12.3M 0s
165600K .......... .......... .......... .......... .......... 99% 96.0M 0s
165650K .......... .......... .......... .......... .......... 99% 20.9M 0s
165700K .......... .......... .......... .......... .......... 99% 24.4M 0s
165750K .......... .......... .......... .......... .......... 99% 26.3M 0s
165800K .......... .......... .......... .......... .......... 99% 22.7M 0s
165850K .......... .......... .......... .......... .......... 99% 35.1M 0s
165900K .......... .......... .......... .......... .......... 99% 16.1M 0s
165950K .......... .......... .......... .......... .......... 99% 10.2M 0s
166000K .......... .......... .......... .......... .......... 99% 26.6M 0s
166050K .......... .......... .......... .......... .......... 99% 17.2M 0s
166100K .......... .......... .......... .......... .......... 99% 115M 0s
166150K .......... .......... .......... .......... .......... 99% 28.9M 0s
166200K .......... .......... .......... .......... .......... 99% 20.9M 0s
166250K .......... .......... .......... .......... .......... 99% 25.0M 0s
166300K .......... .......... .......... .......... .......... 99% 19.4M 0s
166350K .......... .......... .......... .......... .......... 99% 18.9M 0s
166400K .......... .......... .......... .......... .......... 99% 20.2M 0s
166450K .......... .......... .......... .......... .......... 99% 16.5M 0s
166500K .. 100% 3858G=8.3s
2021-01-18 14:38:37 (19.7 MB/s) - ‘cifar-10-python.tar.gz’ saved [170498071/170498071]
tar zxvf cifar-10-python.tar.gz
cifar-10-batches-py/
cifar-10-batches-py/data_batch_4
cifar-10-batches-py/readme.html
cifar-10-batches-py/test_batch
cifar-10-batches-py/data_batch_3
cifar-10-batches-py/batches.meta
cifar-10-batches-py/data_batch_2
cifar-10-batches-py/data_batch_5
cifar-10-batches-py/data_batch_1
ls -la cifar-10-batches-py
total 181884
drwxr-xr-x 2 2156 1103 4096 Jun 4 2009 .
drwxr-xr-x 1 root root 4096 Jan 18 14:38 ..
-rw-r--r-- 1 2156 1103 158 Mar 31 2009 batches.meta
-rw-r--r-- 1 2156 1103 31035704 Mar 31 2009 data_batch_1
-rw-r--r-- 1 2156 1103 31035320 Mar 31 2009 data_batch_2
-rw-r--r-- 1 2156 1103 31035999 Mar 31 2009 data_batch_3
-rw-r--r-- 1 2156 1103 31035696 Mar 31 2009 data_batch_4
-rw-r--r-- 1 2156 1103 31035623 Mar 31 2009 data_batch_5
-rw-r--r-- 1 2156 1103 88 Jun 4 2009 readme.html
-rw-r--r-- 1 2156 1103 31035526 Mar 31 2009 test_batch
Recall the classes are: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck
Here is the code to unpickle the batches.
Loaded in this way, each of the batch files contains a dictionary with the following elements:
- data - a 10000x3072 numpy array of uint8s. Each row of the array stores a 32x32 colour image. The first 1024 entries contain the red channel values, the next 1024 the green, and the final 1024 the blue. The image is stored in row-major order, so that the first 32 entries of the array are the red channel values of the first row of the image.
- labels - a list of 10000 numbers in the range 0-9. The number at index i indicates the label of the ith image in the array data.
def unpickle(file):
import pickle
with open(file, 'rb') as fo:
dict = pickle.load(fo, encoding='bytes')# for Python 3, add the following param: encoding='bytes'
return dict
dir = 'cifar-10-batches-py/'
batches = [unpickle(dir + 'data_batch_' + str(1+n)) for n in range(5)]
Now we need to reshape the data batches and concatenate the training batches into one big tensor.
import numpy as np
def decode(xy):
x_train = np.reshape(xy[b'data'], (10000, 3, 32, 32)).transpose(0, 2, 3, 1)
y_train = np.reshape(xy[b'labels'], (10000, 1))
return (x_train, y_train)
decoded = [decode(data) for data in batches]
x_train = np.concatenate([data[0] for data in decoded])
y_train = np.concatenate([data[1] for data in decoded])
(x_test, y_test) = decode(unpickle(dir + 'test_batch'))
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
x_train shape: (50000, 32, 32, 3)
50000 train samples
10000 test samples
Let's visualize some of the images:
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(36):
fig.add_subplot(6, 6, i+1)
plt.imshow(x_train[i])
display(fig)
Recall that we are getting a categorical output via softmax across 10 neurons, corresponding to the output categories.
So we want to reshape our target values (training labels) to be 1-hot encoded, and Keras can calculate categorical crossentropy between its output layer and the target:
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
num_classes = 10
# Convert class vectors to binary class matrices.
y_train_1hot = keras.utils.to_categorical(y_train, num_classes)
y_test_1hot = keras.utils.to_categorical(y_test, num_classes)
Using TensorFlow backend.
Here's a simple convolutional net to get you started. It will get you to over 57% accuracy in 5 epochs.
As inspiration, with a suitable network and parameters, it's possible to get over 99% test accuracy, although you won't have time to get there in today's session on this hardware.
note: if your network is not learning anything at all -- meaning regardless of settings, you're seeing a loss that doesn't decrease and a validation accuracy that is 10% (i.e., random chance) -- then restart your cluster
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Flatten())
model.add(Dense(64))
model.add(Activation('relu'))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer="adam", metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
history = model.fit(x_train, y_train_1hot,
batch_size=64,
epochs=5,
validation_data=(x_test, y_test_1hot),
verbose=2)
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 50000 samples, validate on 10000 samples
Epoch 1/5
In this session, you probably won't have time to run each experiment for too many epochs ... but you can use this code to plot the training and validation losses:
fig, ax = plt.subplots()
fig.set_size_inches((5,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
display(fig)
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Please feel free to refer to basic concepts here:
- Udacity's course on Deep Learning https://www.udacity.com/course/deep-learning--ud730 by Google engineers: Arpan Chakraborty and Vincent Vanhoucke and their full video playlist:
Entering the 4th Dimension
Networks for Understanding Time-Oriented Patterns in Data
Common time-based problems include * Sequence modeling: "What comes next?" * Likely next letter, word, phrase, category, cound, action, value * Sequence-to-Sequence modeling: "What alternative sequence is a pattern match?" (i.e., similar probability distribution) * Machine translation, text-to-speech/speech-to-text, connected handwriting (specific scripts)

Simplified Approaches
- If we know all of the sequence states and the probabilities of state transition...
- ... then we have a simple Markov Chain model.
- If we don't know all of the states or probabilities (yet) but can make constraining assumptions and acquire solid information from observing (sampling) them...
- ... we can use a Hidden Markov Model approach.
These approached have only limited capacity because they are effectively stateless and so have some degree of "extreme retrograde amnesia."
Can we use a neural network to learn the "next" record in a sequence?
First approach, using what we already know, might look like * Clamp input sequence to a vector of neurons in a feed-forward network * Learn a model on the class of the next input record
Let's try it! This can work in some situations, although it's more of a setup and starting point for our next development.
We will make up a simple example of the English alphabet sequence wehere we try to predict the next alphabet from a sequence of length 3.
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print (seq_in, '->', seq_out)
ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z
# dataX is just a reindexing of the alphabets in consecutive triplets of numbers
dataX
dataY # just a reindexing of the following alphabet after each consecutive triplet of numbers
Train a network on that data:
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM # <- this is the Long-Short-term memory layer
from keras.utils import np_utils
# begin data generation ------------------------------------------
# this is just a repeat of what we did above
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print (seq_in, '->', seq_out)
# end data generation ---------------------------------------------
X = numpy.reshape(dataX, (len(dataX), seq_length))
X = X / float(len(alphabet)) # normalize the mapping of alphabets from integers into [0, 1]
y = np_utils.to_categorical(dataY) # make the output we want to predict to be categorical
# keras architecturing of a feed forward dense or fully connected Neural Network
model = Sequential()
# draw the architecture of the network given by next two lines, hint: X.shape[1] = 3, y.shape[1] = 26
model.add(Dense(30, input_dim=X.shape[1], kernel_initializer='normal', activation='relu'))
model.add(Dense(y.shape[1], activation='softmax'))
# keras compiling and fitting
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=1000, batch_size=5, verbose=2)
scores = model.evaluate(X, y)
print("Model Accuracy: %.2f " % scores[1])
for pattern in dataX:
x = numpy.reshape(pattern, (1, len(pattern)))
x = x / float(len(alphabet))
prediction = model.predict(x, verbose=0) # get prediction from fitted model
index = numpy.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
print (seq_in, "->", result) # print the predicted outputs
Using TensorFlow backend.
ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Epoch 1/1000
- 1s - loss: 3.2612 - acc: 0.0435
Epoch 2/1000
- 0s - loss: 3.2585 - acc: 0.0435
Epoch 3/1000
- 0s - loss: 3.2564 - acc: 0.0435
Epoch 4/1000
- 0s - loss: 3.2543 - acc: 0.0435
Epoch 5/1000
- 0s - loss: 3.2529 - acc: 0.0435
Epoch 6/1000
- 0s - loss: 3.2507 - acc: 0.0435
Epoch 7/1000
- 0s - loss: 3.2491 - acc: 0.0435
Epoch 8/1000
- 0s - loss: 3.2473 - acc: 0.0435
Epoch 9/1000
- 0s - loss: 3.2455 - acc: 0.0435
Epoch 10/1000
- 0s - loss: 3.2438 - acc: 0.0435
Epoch 11/1000
- 0s - loss: 3.2415 - acc: 0.0435
Epoch 12/1000
- 0s - loss: 3.2398 - acc: 0.0435
Epoch 13/1000
- 0s - loss: 3.2378 - acc: 0.0435
Epoch 14/1000
- 0s - loss: 3.2354 - acc: 0.0435
Epoch 15/1000
- 0s - loss: 3.2336 - acc: 0.0435
Epoch 16/1000
- 0s - loss: 3.2313 - acc: 0.0435
Epoch 17/1000
- 0s - loss: 3.2293 - acc: 0.0435
Epoch 18/1000
- 0s - loss: 3.2268 - acc: 0.0435
Epoch 19/1000
- 0s - loss: 3.2248 - acc: 0.0435
Epoch 20/1000
- 0s - loss: 3.2220 - acc: 0.0435
Epoch 21/1000
- 0s - loss: 3.2196 - acc: 0.0435
Epoch 22/1000
- 0s - loss: 3.2168 - acc: 0.0435
Epoch 23/1000
- 0s - loss: 3.2137 - acc: 0.0435
Epoch 24/1000
- 0s - loss: 3.2111 - acc: 0.0435
Epoch 25/1000
- 0s - loss: 3.2082 - acc: 0.0435
Epoch 26/1000
- 0s - loss: 3.2047 - acc: 0.0435
Epoch 27/1000
- 0s - loss: 3.2018 - acc: 0.0435
Epoch 28/1000
- 0s - loss: 3.1984 - acc: 0.0435
Epoch 29/1000
- 0s - loss: 3.1950 - acc: 0.0435
Epoch 30/1000
- 0s - loss: 3.1918 - acc: 0.0435
Epoch 31/1000
- 0s - loss: 3.1883 - acc: 0.0435
Epoch 32/1000
- 0s - loss: 3.1849 - acc: 0.0435
Epoch 33/1000
- 0s - loss: 3.1808 - acc: 0.0435
Epoch 34/1000
- 0s - loss: 3.1776 - acc: 0.0435
Epoch 35/1000
- 0s - loss: 3.1736 - acc: 0.0435
Epoch 36/1000
- 0s - loss: 3.1700 - acc: 0.0435
Epoch 37/1000
- 0s - loss: 3.1655 - acc: 0.0435
Epoch 38/1000
- 0s - loss: 3.1618 - acc: 0.0870
Epoch 39/1000
- 0s - loss: 3.1580 - acc: 0.0435
Epoch 40/1000
- 0s - loss: 3.1533 - acc: 0.0870
Epoch 41/1000
- 0s - loss: 3.1487 - acc: 0.0870
Epoch 42/1000
- 0s - loss: 3.1447 - acc: 0.0870
Epoch 43/1000
- 0s - loss: 3.1408 - acc: 0.0870
Epoch 44/1000
- 0s - loss: 3.1361 - acc: 0.0870
Epoch 45/1000
- 0s - loss: 3.1317 - acc: 0.0870
Epoch 46/1000
- 0s - loss: 3.1275 - acc: 0.0870
Epoch 47/1000
- 0s - loss: 3.1233 - acc: 0.0870
Epoch 48/1000
- 0s - loss: 3.1188 - acc: 0.0870
Epoch 49/1000
- 0s - loss: 3.1142 - acc: 0.0870
Epoch 50/1000
- 0s - loss: 3.1099 - acc: 0.0870
Epoch 51/1000
- 0s - loss: 3.1051 - acc: 0.0870
Epoch 52/1000
- 0s - loss: 3.1007 - acc: 0.0870
Epoch 53/1000
- 0s - loss: 3.0963 - acc: 0.0870
Epoch 54/1000
- 0s - loss: 3.0913 - acc: 0.0870
Epoch 55/1000
- 0s - loss: 3.0875 - acc: 0.0870
Epoch 56/1000
- 0s - loss: 3.0825 - acc: 0.0870
Epoch 57/1000
- 0s - loss: 3.0783 - acc: 0.0870
Epoch 58/1000
- 0s - loss: 3.0732 - acc: 0.0870
Epoch 59/1000
- 0s - loss: 3.0685 - acc: 0.0870
Epoch 60/1000
- 0s - loss: 3.0644 - acc: 0.0870
Epoch 61/1000
- 0s - loss: 3.0596 - acc: 0.0870
Epoch 62/1000
- 0s - loss: 3.0550 - acc: 0.1304
Epoch 63/1000
- 0s - loss: 3.0505 - acc: 0.0870
Epoch 64/1000
- 0s - loss: 3.0458 - acc: 0.0870
Epoch 65/1000
- 0s - loss: 3.0419 - acc: 0.0870
Epoch 66/1000
- 0s - loss: 3.0368 - acc: 0.0870
Epoch 67/1000
- 0s - loss: 3.0327 - acc: 0.0870
Epoch 68/1000
- 0s - loss: 3.0282 - acc: 0.0870
Epoch 69/1000
- 0s - loss: 3.0232 - acc: 0.0870
Epoch 70/1000
- 0s - loss: 3.0189 - acc: 0.0870
Epoch 71/1000
- 0s - loss: 3.0139 - acc: 0.0870
Epoch 72/1000
- 0s - loss: 3.0093 - acc: 0.0870
Epoch 73/1000
- 0s - loss: 3.0049 - acc: 0.0870
Epoch 74/1000
- 0s - loss: 3.0006 - acc: 0.0870
Epoch 75/1000
- 0s - loss: 2.9953 - acc: 0.0870
Epoch 76/1000
- 0s - loss: 2.9910 - acc: 0.0870
Epoch 77/1000
- 0s - loss: 2.9868 - acc: 0.0870
Epoch 78/1000
- 0s - loss: 2.9826 - acc: 0.0870
Epoch 79/1000
- 0s - loss: 2.9773 - acc: 0.0870
Epoch 80/1000
- 0s - loss: 2.9728 - acc: 0.0870
Epoch 81/1000
- 0s - loss: 2.9683 - acc: 0.0870
Epoch 82/1000
- 0s - loss: 2.9640 - acc: 0.0870
Epoch 83/1000
- 0s - loss: 2.9594 - acc: 0.0870
Epoch 84/1000
- 0s - loss: 2.9550 - acc: 0.0870
Epoch 85/1000
- 0s - loss: 2.9508 - acc: 0.0870
Epoch 86/1000
- 0s - loss: 2.9461 - acc: 0.0870
Epoch 87/1000
- 0s - loss: 2.9415 - acc: 0.0870
Epoch 88/1000
- 0s - loss: 2.9372 - acc: 0.0870
Epoch 89/1000
- 0s - loss: 2.9331 - acc: 0.1304
Epoch 90/1000
- 0s - loss: 2.9284 - acc: 0.1304
Epoch 91/1000
- 0s - loss: 2.9239 - acc: 0.1304
Epoch 92/1000
- 0s - loss: 2.9192 - acc: 0.1304
Epoch 93/1000
- 0s - loss: 2.9148 - acc: 0.1304
Epoch 94/1000
- 0s - loss: 2.9105 - acc: 0.1304
Epoch 95/1000
- 0s - loss: 2.9061 - acc: 0.1304
Epoch 96/1000
- 0s - loss: 2.9018 - acc: 0.1304
Epoch 97/1000
- 0s - loss: 2.8975 - acc: 0.1304
Epoch 98/1000
- 0s - loss: 2.8932 - acc: 0.1304
Epoch 99/1000
- 0s - loss: 2.8889 - acc: 0.1304
Epoch 100/1000
- 0s - loss: 2.8844 - acc: 0.1304
Epoch 101/1000
- 0s - loss: 2.8803 - acc: 0.1304
Epoch 102/1000
- 0s - loss: 2.8758 - acc: 0.1304
Epoch 103/1000
- 0s - loss: 2.8717 - acc: 0.1304
Epoch 104/1000
- 0s - loss: 2.8674 - acc: 0.0870
Epoch 105/1000
- 0s - loss: 2.8634 - acc: 0.0870
Epoch 106/1000
- 0s - loss: 2.8586 - acc: 0.0870
Epoch 107/1000
- 0s - loss: 2.8547 - acc: 0.0870
Epoch 108/1000
- 0s - loss: 2.8505 - acc: 0.0870
Epoch 109/1000
- 0s - loss: 2.8462 - acc: 0.0870
Epoch 110/1000
- 0s - loss: 2.8421 - acc: 0.0870
Epoch 111/1000
- 0s - loss: 2.8383 - acc: 0.0870
Epoch 112/1000
- 0s - loss: 2.8337 - acc: 0.0870
Epoch 113/1000
- 0s - loss: 2.8299 - acc: 0.0870
Epoch 114/1000
- 0s - loss: 2.8257 - acc: 0.0870
Epoch 115/1000
- 0s - loss: 2.8216 - acc: 0.0870
Epoch 116/1000
- 0s - loss: 2.8173 - acc: 0.0870
Epoch 117/1000
- 0s - loss: 2.8134 - acc: 0.0870
Epoch 118/1000
- 0s - loss: 2.8094 - acc: 0.0870
Epoch 119/1000
- 0s - loss: 2.8058 - acc: 0.0870
Epoch 120/1000
- 0s - loss: 2.8016 - acc: 0.0870
Epoch 121/1000
- 0s - loss: 2.7975 - acc: 0.1304
Epoch 122/1000
- 0s - loss: 2.7934 - acc: 0.1304
Epoch 123/1000
- 0s - loss: 2.7895 - acc: 0.1304
Epoch 124/1000
- 0s - loss: 2.7858 - acc: 0.1304
Epoch 125/1000
- 0s - loss: 2.7820 - acc: 0.1304
Epoch 126/1000
- 0s - loss: 2.7782 - acc: 0.1304
Epoch 127/1000
- 0s - loss: 2.7738 - acc: 0.1304
Epoch 128/1000
- 0s - loss: 2.7696 - acc: 0.1304
Epoch 129/1000
- 0s - loss: 2.7661 - acc: 0.1304
Epoch 130/1000
- 0s - loss: 2.7625 - acc: 0.1304
Epoch 131/1000
- 0s - loss: 2.7587 - acc: 0.1304
Epoch 132/1000
- 0s - loss: 2.7547 - acc: 0.1304
Epoch 133/1000
- 0s - loss: 2.7513 - acc: 0.1304
Epoch 134/1000
- 0s - loss: 2.7476 - acc: 0.1304
Epoch 135/1000
- 0s - loss: 2.7436 - acc: 0.1304
Epoch 136/1000
- 0s - loss: 2.7398 - acc: 0.1304
Epoch 137/1000
- 0s - loss: 2.7365 - acc: 0.0870
Epoch 138/1000
- 0s - loss: 2.7326 - acc: 0.0870
Epoch 139/1000
- 0s - loss: 2.7288 - acc: 0.1304
Epoch 140/1000
- 0s - loss: 2.7250 - acc: 0.1304
Epoch 141/1000
- 0s - loss: 2.7215 - acc: 0.1304
Epoch 142/1000
- 0s - loss: 2.7182 - acc: 0.1304
Epoch 143/1000
- 0s - loss: 2.7148 - acc: 0.1304
Epoch 144/1000
- 0s - loss: 2.7112 - acc: 0.1304
Epoch 145/1000
- 0s - loss: 2.7077 - acc: 0.1304
Epoch 146/1000
- 0s - loss: 2.7041 - acc: 0.1304
Epoch 147/1000
- 0s - loss: 2.7010 - acc: 0.1304
Epoch 148/1000
- 0s - loss: 2.6973 - acc: 0.1304
Epoch 149/1000
- 0s - loss: 2.6939 - acc: 0.0870
Epoch 150/1000
- 0s - loss: 2.6910 - acc: 0.0870
Epoch 151/1000
- 0s - loss: 2.6873 - acc: 0.0870
Epoch 152/1000
- 0s - loss: 2.6839 - acc: 0.0870
Epoch 153/1000
- 0s - loss: 2.6805 - acc: 0.1304
Epoch 154/1000
- 0s - loss: 2.6773 - acc: 0.1304
Epoch 155/1000
- 0s - loss: 2.6739 - acc: 0.1304
Epoch 156/1000
- 0s - loss: 2.6707 - acc: 0.1739
Epoch 157/1000
- 0s - loss: 2.6676 - acc: 0.1739
Epoch 158/1000
- 0s - loss: 2.6639 - acc: 0.1739
Epoch 159/1000
- 0s - loss: 2.6608 - acc: 0.1739
Epoch 160/1000
- 0s - loss: 2.6577 - acc: 0.1739
Epoch 161/1000
- 0s - loss: 2.6542 - acc: 0.1739
Epoch 162/1000
- 0s - loss: 2.6513 - acc: 0.1739
Epoch 163/1000
- 0s - loss: 2.6479 - acc: 0.1739
Epoch 164/1000
- 0s - loss: 2.6447 - acc: 0.1739
Epoch 165/1000
- 0s - loss: 2.6420 - acc: 0.1739
Epoch 166/1000
- 0s - loss: 2.6386 - acc: 0.1739
Epoch 167/1000
- 0s - loss: 2.6355 - acc: 0.1739
Epoch 168/1000
- 0s - loss: 2.6327 - acc: 0.1739
Epoch 169/1000
- 0s - loss: 2.6296 - acc: 0.1739
Epoch 170/1000
- 0s - loss: 2.6268 - acc: 0.1739
Epoch 171/1000
- 0s - loss: 2.6235 - acc: 0.1739
Epoch 172/1000
- 0s - loss: 2.6203 - acc: 0.1739
Epoch 173/1000
- 0s - loss: 2.6179 - acc: 0.1739
Epoch 174/1000
- 0s - loss: 2.6147 - acc: 0.1739
Epoch 175/1000
- 0s - loss: 2.6121 - acc: 0.1739
Epoch 176/1000
- 0s - loss: 2.6088 - acc: 0.1739
Epoch 177/1000
- 0s - loss: 2.6058 - acc: 0.1739
Epoch 178/1000
- 0s - loss: 2.6034 - acc: 0.1739
Epoch 179/1000
- 0s - loss: 2.6001 - acc: 0.1739
Epoch 180/1000
- 0s - loss: 2.5969 - acc: 0.1739
Epoch 181/1000
- 0s - loss: 2.5945 - acc: 0.1739
Epoch 182/1000
- 0s - loss: 2.5921 - acc: 0.1739
Epoch 183/1000
- 0s - loss: 2.5886 - acc: 0.1739
Epoch 184/1000
- 0s - loss: 2.5862 - acc: 0.1739
Epoch 185/1000
- 0s - loss: 2.5837 - acc: 0.1304
Epoch 186/1000
- 0s - loss: 2.5805 - acc: 0.1739
Epoch 187/1000
- 0s - loss: 2.5778 - acc: 0.1739
Epoch 188/1000
- 0s - loss: 2.5753 - acc: 0.1739
Epoch 189/1000
- 0s - loss: 2.5727 - acc: 0.1739
Epoch 190/1000
- 0s - loss: 2.5695 - acc: 0.1739
Epoch 191/1000
- 0s - loss: 2.5669 - acc: 0.1739
Epoch 192/1000
- 0s - loss: 2.5643 - acc: 0.1739
Epoch 193/1000
- 0s - loss: 2.5614 - acc: 0.1739
Epoch 194/1000
- 0s - loss: 2.5591 - acc: 0.1739
Epoch 195/1000
- 0s - loss: 2.5566 - acc: 0.1739
Epoch 196/1000
- 0s - loss: 2.5535 - acc: 0.1739
Epoch 197/1000
- 0s - loss: 2.5511 - acc: 0.1739
Epoch 198/1000
- 0s - loss: 2.5484 - acc: 0.1739
Epoch 199/1000
- 0s - loss: 2.5458 - acc: 0.1739
Epoch 200/1000
- 0s - loss: 2.5433 - acc: 0.1739
Epoch 201/1000
- 0s - loss: 2.5411 - acc: 0.1739
Epoch 202/1000
- 0s - loss: 2.5383 - acc: 0.1739
Epoch 203/1000
- 0s - loss: 2.5357 - acc: 0.1739
Epoch 204/1000
- 0s - loss: 2.5328 - acc: 0.1739
Epoch 205/1000
- 0s - loss: 2.5308 - acc: 0.1739
Epoch 206/1000
- 0s - loss: 2.5281 - acc: 0.1739
Epoch 207/1000
- 0s - loss: 2.5261 - acc: 0.1739
Epoch 208/1000
- 0s - loss: 2.5237 - acc: 0.1739
Epoch 209/1000
- 0s - loss: 2.5208 - acc: 0.1739
Epoch 210/1000
- 0s - loss: 2.5189 - acc: 0.1739
Epoch 211/1000
- 0s - loss: 2.5162 - acc: 0.1739
Epoch 212/1000
- 0s - loss: 2.5136 - acc: 0.1739
Epoch 213/1000
- 0s - loss: 2.5111 - acc: 0.1739
Epoch 214/1000
- 0s - loss: 2.5088 - acc: 0.1739
Epoch 215/1000
- 0s - loss: 2.5066 - acc: 0.1739
Epoch 216/1000
- 0s - loss: 2.5041 - acc: 0.1739
Epoch 217/1000
- 0s - loss: 2.5018 - acc: 0.1739
Epoch 218/1000
- 0s - loss: 2.4993 - acc: 0.1739
Epoch 219/1000
- 0s - loss: 2.4968 - acc: 0.1739
Epoch 220/1000
- 0s - loss: 2.4947 - acc: 0.1739
Epoch 221/1000
- 0s - loss: 2.4922 - acc: 0.1739
Epoch 222/1000
- 0s - loss: 2.4898 - acc: 0.1739
Epoch 223/1000
- 0s - loss: 2.4878 - acc: 0.1739
Epoch 224/1000
- 0s - loss: 2.4856 - acc: 0.1739
Epoch 225/1000
- 0s - loss: 2.4833 - acc: 0.1739
Epoch 226/1000
- 0s - loss: 2.4808 - acc: 0.1739
Epoch 227/1000
- 0s - loss: 2.4786 - acc: 0.1739
Epoch 228/1000
- 0s - loss: 2.4763 - acc: 0.1739
Epoch 229/1000
- 0s - loss: 2.4739 - acc: 0.1739
Epoch 230/1000
- 0s - loss: 2.4722 - acc: 0.1739
Epoch 231/1000
- 0s - loss: 2.4699 - acc: 0.1739
Epoch 232/1000
- 0s - loss: 2.4681 - acc: 0.1739
Epoch 233/1000
- 0s - loss: 2.4658 - acc: 0.1739
Epoch 234/1000
- 0s - loss: 2.4633 - acc: 0.1739
Epoch 235/1000
- 0s - loss: 2.4612 - acc: 0.1739
Epoch 236/1000
- 0s - loss: 2.4589 - acc: 0.1739
Epoch 237/1000
- 0s - loss: 2.4569 - acc: 0.1739
Epoch 238/1000
- 0s - loss: 2.4543 - acc: 0.1739
Epoch 239/1000
- 0s - loss: 2.4524 - acc: 0.1739
Epoch 240/1000
- 0s - loss: 2.4505 - acc: 0.1739
Epoch 241/1000
- 0s - loss: 2.4487 - acc: 0.1739
Epoch 242/1000
- 0s - loss: 2.4464 - acc: 0.1739
Epoch 243/1000
- 0s - loss: 2.4440 - acc: 0.1739
Epoch 244/1000
- 0s - loss: 2.4420 - acc: 0.1739
Epoch 245/1000
- 0s - loss: 2.4405 - acc: 0.1739
Epoch 246/1000
- 0s - loss: 2.4380 - acc: 0.2174
Epoch 247/1000
- 0s - loss: 2.4362 - acc: 0.2174
Epoch 248/1000
- 0s - loss: 2.4340 - acc: 0.2174
Epoch 249/1000
- 0s - loss: 2.4324 - acc: 0.2174
Epoch 250/1000
- 0s - loss: 2.4301 - acc: 0.2174
Epoch 251/1000
- 0s - loss: 2.4284 - acc: 0.2174
Epoch 252/1000
- 0s - loss: 2.4260 - acc: 0.2174
Epoch 253/1000
- 0s - loss: 2.4239 - acc: 0.2174
Epoch 254/1000
- 0s - loss: 2.4217 - acc: 0.2174
Epoch 255/1000
- 0s - loss: 2.4200 - acc: 0.2174
Epoch 256/1000
- 0s - loss: 2.4182 - acc: 0.2174
Epoch 257/1000
- 0s - loss: 2.4160 - acc: 0.2174
Epoch 258/1000
- 0s - loss: 2.4142 - acc: 0.2174
Epoch 259/1000
- 0s - loss: 2.4125 - acc: 0.2174
Epoch 260/1000
- 0s - loss: 2.4102 - acc: 0.1739
Epoch 261/1000
- 0s - loss: 2.4084 - acc: 0.1739
Epoch 262/1000
- 0s - loss: 2.4060 - acc: 0.1739
Epoch 263/1000
- 0s - loss: 2.4044 - acc: 0.1739
Epoch 264/1000
- 0s - loss: 2.4028 - acc: 0.2174
Epoch 265/1000
- 0s - loss: 2.4008 - acc: 0.2174
Epoch 266/1000
- 0s - loss: 2.3985 - acc: 0.2174
Epoch 267/1000
- 0s - loss: 2.3964 - acc: 0.2174
Epoch 268/1000
- 0s - loss: 2.3951 - acc: 0.1739
Epoch 269/1000
- 0s - loss: 2.3931 - acc: 0.2174
Epoch 270/1000
- 0s - loss: 2.3910 - acc: 0.2174
Epoch 271/1000
- 0s - loss: 2.3892 - acc: 0.2174
Epoch 272/1000
- 0s - loss: 2.3876 - acc: 0.2174
Epoch 273/1000
- 0s - loss: 2.3856 - acc: 0.2174
Epoch 274/1000
- 0s - loss: 2.3837 - acc: 0.2174
Epoch 275/1000
- 0s - loss: 2.3823 - acc: 0.2174
Epoch 276/1000
- 0s - loss: 2.3807 - acc: 0.2174
Epoch 277/1000
- 0s - loss: 2.3786 - acc: 0.2609
Epoch 278/1000
- 0s - loss: 2.3770 - acc: 0.2609
Epoch 279/1000
- 0s - loss: 2.3749 - acc: 0.2609
Epoch 280/1000
- 0s - loss: 2.3735 - acc: 0.2609
Epoch 281/1000
- 0s - loss: 2.3718 - acc: 0.2609
Epoch 282/1000
- 0s - loss: 2.3697 - acc: 0.2609
Epoch 283/1000
- 0s - loss: 2.3677 - acc: 0.2609
Epoch 284/1000
- 0s - loss: 2.3665 - acc: 0.2174
Epoch 285/1000
- 0s - loss: 2.3643 - acc: 0.2174
Epoch 286/1000
- 0s - loss: 2.3627 - acc: 0.2174
Epoch 287/1000
- 0s - loss: 2.3609 - acc: 0.1739
Epoch 288/1000
- 0s - loss: 2.3592 - acc: 0.1739
Epoch 289/1000
- 0s - loss: 2.3575 - acc: 0.1739
Epoch 290/1000
- 0s - loss: 2.3560 - acc: 0.1739
Epoch 291/1000
- 0s - loss: 2.3540 - acc: 0.1739
Epoch 292/1000
- 0s - loss: 2.3523 - acc: 0.2174
Epoch 293/1000
- 0s - loss: 2.3506 - acc: 0.2174
Epoch 294/1000
- 0s - loss: 2.3486 - acc: 0.2174
Epoch 295/1000
- 0s - loss: 2.3471 - acc: 0.2174
Epoch 296/1000
- 0s - loss: 2.3451 - acc: 0.2609
Epoch 297/1000
- 0s - loss: 2.3438 - acc: 0.2609
Epoch 298/1000
- 0s - loss: 2.3421 - acc: 0.2609
Epoch 299/1000
- 0s - loss: 2.3398 - acc: 0.2609
Epoch 300/1000
- 0s - loss: 2.3389 - acc: 0.2174
Epoch 301/1000
- 0s - loss: 2.3374 - acc: 0.2174
Epoch 302/1000
- 0s - loss: 2.3356 - acc: 0.2174
Epoch 303/1000
- 0s - loss: 2.3336 - acc: 0.2174
Epoch 304/1000
- 0s - loss: 2.3325 - acc: 0.2174
Epoch 305/1000
- 0s - loss: 2.3305 - acc: 0.2609
Epoch 306/1000
- 0s - loss: 2.3290 - acc: 0.2609
Epoch 307/1000
- 0s - loss: 2.3271 - acc: 0.2609
Epoch 308/1000
- 0s - loss: 2.3256 - acc: 0.2609
Epoch 309/1000
- 0s - loss: 2.3240 - acc: 0.2174
Epoch 310/1000
- 0s - loss: 2.3222 - acc: 0.2174
Epoch 311/1000
- 0s - loss: 2.3204 - acc: 0.2609
Epoch 312/1000
- 0s - loss: 2.3190 - acc: 0.2609
Epoch 313/1000
- 0s - loss: 2.3176 - acc: 0.2609
Epoch 314/1000
- 0s - loss: 2.3155 - acc: 0.2609
Epoch 315/1000
- 0s - loss: 2.3141 - acc: 0.2609
Epoch 316/1000
- 0s - loss: 2.3124 - acc: 0.2609
Epoch 317/1000
- 0s - loss: 2.3112 - acc: 0.2609
Epoch 318/1000
- 0s - loss: 2.3095 - acc: 0.2609
Epoch 319/1000
- 0s - loss: 2.3077 - acc: 0.2609
Epoch 320/1000
- 0s - loss: 2.3061 - acc: 0.2609
Epoch 321/1000
- 0s - loss: 2.3048 - acc: 0.2609
Epoch 322/1000
- 0s - loss: 2.3030 - acc: 0.2609
Epoch 323/1000
- 0s - loss: 2.3016 - acc: 0.2609
Epoch 324/1000
- 0s - loss: 2.3000 - acc: 0.2609
Epoch 325/1000
- 0s - loss: 2.2985 - acc: 0.3043
Epoch 326/1000
- 0s - loss: 2.2965 - acc: 0.3043
Epoch 327/1000
- 0s - loss: 2.2953 - acc: 0.3043
Epoch 328/1000
- 0s - loss: 2.2942 - acc: 0.3043
Epoch 329/1000
- 0s - loss: 2.2920 - acc: 0.3043
Epoch 330/1000
- 0s - loss: 2.2911 - acc: 0.3043
Epoch 331/1000
- 0s - loss: 2.2897 - acc: 0.3043
Epoch 332/1000
- 0s - loss: 2.2880 - acc: 0.3478
Epoch 333/1000
- 0s - loss: 2.2864 - acc: 0.3478
Epoch 334/1000
- 0s - loss: 2.2851 - acc: 0.3043
Epoch 335/1000
- 0s - loss: 2.2839 - acc: 0.3043
Epoch 336/1000
- 0s - loss: 2.2823 - acc: 0.3043
Epoch 337/1000
- 0s - loss: 2.2806 - acc: 0.3043
Epoch 338/1000
- 0s - loss: 2.2795 - acc: 0.3043
Epoch 339/1000
- 0s - loss: 2.2782 - acc: 0.3043
Epoch 340/1000
- 0s - loss: 2.2764 - acc: 0.3043
Epoch 341/1000
- 0s - loss: 2.2749 - acc: 0.3043
Epoch 342/1000
- 0s - loss: 2.2737 - acc: 0.3043
Epoch 343/1000
- 0s - loss: 2.2719 - acc: 0.3043
Epoch 344/1000
- 0s - loss: 2.2707 - acc: 0.3043
Epoch 345/1000
- 0s - loss: 2.2693 - acc: 0.3043
Epoch 346/1000
- 0s - loss: 2.2677 - acc: 0.3043
Epoch 347/1000
- 0s - loss: 2.2663 - acc: 0.3043
Epoch 348/1000
- 0s - loss: 2.2648 - acc: 0.3043
Epoch 349/1000
- 0s - loss: 2.2634 - acc: 0.3043
Epoch 350/1000
- 0s - loss: 2.2622 - acc: 0.3043
Epoch 351/1000
- 0s - loss: 2.2605 - acc: 0.3043
Epoch 352/1000
- 0s - loss: 2.2590 - acc: 0.3043
Epoch 353/1000
- 0s - loss: 2.2574 - acc: 0.3043
Epoch 354/1000
- 0s - loss: 2.2558 - acc: 0.2609
Epoch 355/1000
- 0s - loss: 2.2551 - acc: 0.3043
Epoch 356/1000
- 0s - loss: 2.2536 - acc: 0.3043
Epoch 357/1000
- 0s - loss: 2.2519 - acc: 0.2609
Epoch 358/1000
- 0s - loss: 2.2510 - acc: 0.3043
Epoch 359/1000
- 0s - loss: 2.2496 - acc: 0.3478
Epoch 360/1000
- 0s - loss: 2.2484 - acc: 0.3043
Epoch 361/1000
- 0s - loss: 2.2469 - acc: 0.3043
Epoch 362/1000
- 0s - loss: 2.2451 - acc: 0.3043
Epoch 363/1000
- 0s - loss: 2.2441 - acc: 0.3043
Epoch 364/1000
- 0s - loss: 2.2432 - acc: 0.3478
Epoch 365/1000
- 0s - loss: 2.2409 - acc: 0.3478
Epoch 366/1000
- 0s - loss: 2.2398 - acc: 0.3478
Epoch 367/1000
- 0s - loss: 2.2387 - acc: 0.3478
Epoch 368/1000
- 0s - loss: 2.2372 - acc: 0.3478
Epoch 369/1000
- 0s - loss: 2.2360 - acc: 0.3478
Epoch 370/1000
- 0s - loss: 2.2341 - acc: 0.3043
Epoch 371/1000
- 0s - loss: 2.2331 - acc: 0.3043
Epoch 372/1000
- 0s - loss: 2.2317 - acc: 0.3043
Epoch 373/1000
- 0s - loss: 2.2306 - acc: 0.3043
Epoch 374/1000
- 0s - loss: 2.2293 - acc: 0.3043
Epoch 375/1000
- 0s - loss: 2.2276 - acc: 0.3043
Epoch 376/1000
- 0s - loss: 2.2269 - acc: 0.3043
Epoch 377/1000
- 0s - loss: 2.2250 - acc: 0.2609
Epoch 378/1000
- 0s - loss: 2.2243 - acc: 0.2609
Epoch 379/1000
- 0s - loss: 2.2222 - acc: 0.3043
Epoch 380/1000
- 0s - loss: 2.2212 - acc: 0.3043
Epoch 381/1000
- 0s - loss: 2.2201 - acc: 0.3043
Epoch 382/1000
- 0s - loss: 2.2192 - acc: 0.3043
Epoch 383/1000
- 0s - loss: 2.2177 - acc: 0.3043
Epoch 384/1000
- 0s - loss: 2.2157 - acc: 0.3043
Epoch 385/1000
- 0s - loss: 2.2140 - acc: 0.3043
Epoch 386/1000
- 0s - loss: 2.2137 - acc: 0.3043
Epoch 387/1000
- 0s - loss: 2.2126 - acc: 0.3043
Epoch 388/1000
- 0s - loss: 2.2108 - acc: 0.3043
Epoch 389/1000
- 0s - loss: 2.2098 - acc: 0.2609
Epoch 390/1000
- 0s - loss: 2.2087 - acc: 0.2609
Epoch 391/1000
- 0s - loss: 2.2071 - acc: 0.2609
Epoch 392/1000
- 0s - loss: 2.2063 - acc: 0.2609
Epoch 393/1000
- 0s - loss: 2.2051 - acc: 0.2609
Epoch 394/1000
- 0s - loss: 2.2039 - acc: 0.2609
Epoch 395/1000
- 0s - loss: 2.2025 - acc: 0.3043
Epoch 396/1000
- 0s - loss: 2.2014 - acc: 0.3043
Epoch 397/1000
- 0s - loss: 2.2003 - acc: 0.3043
Epoch 398/1000
- 0s - loss: 2.1987 - acc: 0.3043
Epoch 399/1000
- 0s - loss: 2.1975 - acc: 0.3043
Epoch 400/1000
- 0s - loss: 2.1964 - acc: 0.3043
Epoch 401/1000
- 0s - loss: 2.1952 - acc: 0.2609
Epoch 402/1000
- 0s - loss: 2.1939 - acc: 0.3478
Epoch 403/1000
- 0s - loss: 2.1931 - acc: 0.3478
Epoch 404/1000
- 0s - loss: 2.1917 - acc: 0.3478
Epoch 405/1000
- 0s - loss: 2.1909 - acc: 0.3478
Epoch 406/1000
- 0s - loss: 2.1889 - acc: 0.3913
Epoch 407/1000
- 0s - loss: 2.1872 - acc: 0.3913
Epoch 408/1000
- 0s - loss: 2.1864 - acc: 0.3913
Epoch 409/1000
- 0s - loss: 2.1855 - acc: 0.3478
Epoch 410/1000
- 0s - loss: 2.1845 - acc: 0.3478
Epoch 411/1000
- 0s - loss: 2.1833 - acc: 0.3043
Epoch 412/1000
- 0s - loss: 2.1818 - acc: 0.3043
Epoch 413/1000
- 0s - loss: 2.1809 - acc: 0.3913
Epoch 414/1000
- 0s - loss: 2.1793 - acc: 0.3913
Epoch 415/1000
- 0s - loss: 2.1783 - acc: 0.3913
Epoch 416/1000
- 0s - loss: 2.1774 - acc: 0.3913
Epoch 417/1000
- 0s - loss: 2.1760 - acc: 0.3478
Epoch 418/1000
- 0s - loss: 2.1748 - acc: 0.3478
Epoch 419/1000
- 0s - loss: 2.1728 - acc: 0.3913
Epoch 420/1000
- 0s - loss: 2.1720 - acc: 0.3913
Epoch 421/1000
- 0s - loss: 2.1710 - acc: 0.3913
Epoch 422/1000
- 0s - loss: 2.1697 - acc: 0.3478
Epoch 423/1000
- 0s - loss: 2.1691 - acc: 0.3043
Epoch 424/1000
- 0s - loss: 2.1683 - acc: 0.3043
Epoch 425/1000
- 0s - loss: 2.1665 - acc: 0.3043
Epoch 426/1000
- 0s - loss: 2.1649 - acc: 0.3043
Epoch 427/1000
- 0s - loss: 2.1638 - acc: 0.3043
Epoch 428/1000
- 0s - loss: 2.1636 - acc: 0.3043
Epoch 429/1000
- 0s - loss: 2.1616 - acc: 0.2609
Epoch 430/1000
- 0s - loss: 2.1613 - acc: 0.2609
Epoch 431/1000
- 0s - loss: 2.1594 - acc: 0.3043
Epoch 432/1000
- 0s - loss: 2.1583 - acc: 0.2609
Epoch 433/1000
- 0s - loss: 2.1577 - acc: 0.2609
Epoch 434/1000
- 0s - loss: 2.1565 - acc: 0.2609
Epoch 435/1000
- 0s - loss: 2.1548 - acc: 0.3478
Epoch 436/1000
- 0s - loss: 2.1540 - acc: 0.3478
Epoch 437/1000
- 0s - loss: 2.1530 - acc: 0.3043
Epoch 438/1000
- 0s - loss: 2.1516 - acc: 0.3043
Epoch 439/1000
- 0s - loss: 2.1507 - acc: 0.3043
Epoch 440/1000
- 0s - loss: 2.1492 - acc: 0.3043
Epoch 441/1000
- 0s - loss: 2.1482 - acc: 0.3478
Epoch 442/1000
- 0s - loss: 2.1472 - acc: 0.3043
Epoch 443/1000
- 0s - loss: 2.1463 - acc: 0.2609
Epoch 444/1000
- 0s - loss: 2.1451 - acc: 0.2609
Epoch 445/1000
- 0s - loss: 2.1442 - acc: 0.2609
Epoch 446/1000
- 0s - loss: 2.1427 - acc: 0.2609
Epoch 447/1000
- 0s - loss: 2.1419 - acc: 0.2609
Epoch 448/1000
- 0s - loss: 2.1408 - acc: 0.2609
Epoch 449/1000
- 0s - loss: 2.1398 - acc: 0.3043
Epoch 450/1000
- 0s - loss: 2.1390 - acc: 0.3043
Epoch 451/1000
- 0s - loss: 2.1379 - acc: 0.3043
Epoch 452/1000
- 0s - loss: 2.1373 - acc: 0.3478
Epoch 453/1000
- 0s - loss: 2.1356 - acc: 0.3478
Epoch 454/1000
- 0s - loss: 2.1344 - acc: 0.3478
Epoch 455/1000
- 0s - loss: 2.1334 - acc: 0.3478
Epoch 456/1000
- 0s - loss: 2.1323 - acc: 0.3478
Epoch 457/1000
- 0s - loss: 2.1311 - acc: 0.3478
Epoch 458/1000
- 0s - loss: 2.1303 - acc: 0.3478
Epoch 459/1000
- 0s - loss: 2.1290 - acc: 0.3913
Epoch 460/1000
- 0s - loss: 2.1290 - acc: 0.3913
Epoch 461/1000
- 0s - loss: 2.1275 - acc: 0.3913
Epoch 462/1000
- 0s - loss: 2.1268 - acc: 0.3913
Epoch 463/1000
- 0s - loss: 2.1254 - acc: 0.3913
Epoch 464/1000
- 0s - loss: 2.1248 - acc: 0.3478
Epoch 465/1000
- 0s - loss: 2.1233 - acc: 0.3478
Epoch 466/1000
- 0s - loss: 2.1217 - acc: 0.3478
Epoch 467/1000
- 0s - loss: 2.1209 - acc: 0.3478
Epoch 468/1000
- 0s - loss: 2.1197 - acc: 0.3478
Epoch 469/1000
- 0s - loss: 2.1190 - acc: 0.3478
Epoch 470/1000
- 0s - loss: 2.1176 - acc: 0.3478
Epoch 471/1000
- 0s - loss: 2.1166 - acc: 0.3478
Epoch 472/1000
- 0s - loss: 2.1158 - acc: 0.3913
Epoch 473/1000
- 0s - loss: 2.1149 - acc: 0.3913
Epoch 474/1000
- 0s - loss: 2.1135 - acc: 0.4348
Epoch 475/1000
- 0s - loss: 2.1131 - acc: 0.3913
Epoch 476/1000
- 0s - loss: 2.1111 - acc: 0.3478
Epoch 477/1000
- 0s - loss: 2.1099 - acc: 0.3478
Epoch 478/1000
- 0s - loss: 2.1093 - acc: 0.3478
Epoch 479/1000
- 0s - loss: 2.1085 - acc: 0.3478
Epoch 480/1000
- 0s - loss: 2.1074 - acc: 0.3478
Epoch 481/1000
- 0s - loss: 2.1064 - acc: 0.3478
Epoch 482/1000
- 0s - loss: 2.1057 - acc: 0.3478
Epoch 483/1000
- 0s - loss: 2.1044 - acc: 0.3478
Epoch 484/1000
- 0s - loss: 2.1031 - acc: 0.3478
Epoch 485/1000
- 0s - loss: 2.1026 - acc: 0.3478
Epoch 486/1000
- 0s - loss: 2.1018 - acc: 0.3478
Epoch 487/1000
*** WARNING: skipped 1250 bytes of output ***
- 0s - loss: 2.0758 - acc: 0.3478
Epoch 513/1000
- 0s - loss: 2.0741 - acc: 0.3478
Epoch 514/1000
- 0s - loss: 2.0739 - acc: 0.3478
Epoch 515/1000
- 0s - loss: 2.0735 - acc: 0.4348
Epoch 516/1000
- 0s - loss: 2.0723 - acc: 0.3478
Epoch 517/1000
- 0s - loss: 2.0711 - acc: 0.3913
Epoch 518/1000
- 0s - loss: 2.0699 - acc: 0.3478
Epoch 519/1000
- 0s - loss: 2.0691 - acc: 0.3913
Epoch 520/1000
- 0s - loss: 2.0681 - acc: 0.3913
Epoch 521/1000
- 0s - loss: 2.0679 - acc: 0.3913
Epoch 522/1000
- 0s - loss: 2.0664 - acc: 0.3913
Epoch 523/1000
- 0s - loss: 2.0655 - acc: 0.3913
Epoch 524/1000
- 0s - loss: 2.0643 - acc: 0.3913
Epoch 525/1000
- 0s - loss: 2.0632 - acc: 0.3478
Epoch 526/1000
- 0s - loss: 2.0621 - acc: 0.3913
Epoch 527/1000
- 0s - loss: 2.0618 - acc: 0.3478
Epoch 528/1000
- 0s - loss: 2.0610 - acc: 0.3478
Epoch 529/1000
- 0s - loss: 2.0601 - acc: 0.3478
Epoch 530/1000
- 0s - loss: 2.0585 - acc: 0.3478
Epoch 531/1000
- 0s - loss: 2.0578 - acc: 0.3913
Epoch 532/1000
- 0s - loss: 2.0568 - acc: 0.3913
Epoch 533/1000
- 0s - loss: 2.0561 - acc: 0.4348
Epoch 534/1000
- 0s - loss: 2.0554 - acc: 0.4783
Epoch 535/1000
- 0s - loss: 2.0546 - acc: 0.3913
Epoch 536/1000
- 0s - loss: 2.0535 - acc: 0.3913
Epoch 537/1000
- 0s - loss: 2.0527 - acc: 0.3913
Epoch 538/1000
- 0s - loss: 2.0520 - acc: 0.3913
Epoch 539/1000
- 0s - loss: 2.0507 - acc: 0.3913
Epoch 540/1000
- 0s - loss: 2.0493 - acc: 0.3913
Epoch 541/1000
- 0s - loss: 2.0489 - acc: 0.4783
Epoch 542/1000
- 0s - loss: 2.0478 - acc: 0.4783
Epoch 543/1000
- 0s - loss: 2.0464 - acc: 0.4783
Epoch 544/1000
- 0s - loss: 2.0468 - acc: 0.4783
Epoch 545/1000
- 0s - loss: 2.0455 - acc: 0.5217
Epoch 546/1000
- 0s - loss: 2.0441 - acc: 0.5652
Epoch 547/1000
- 0s - loss: 2.0431 - acc: 0.5652
Epoch 548/1000
- 0s - loss: 2.0423 - acc: 0.5652
Epoch 549/1000
- 0s - loss: 2.0412 - acc: 0.5652
Epoch 550/1000
- 0s - loss: 2.0405 - acc: 0.5652
Epoch 551/1000
- 0s - loss: 2.0399 - acc: 0.5217
Epoch 552/1000
- 0s - loss: 2.0390 - acc: 0.5217
Epoch 553/1000
- 0s - loss: 2.0379 - acc: 0.5217
Epoch 554/1000
- 0s - loss: 2.0372 - acc: 0.5217
Epoch 555/1000
- 0s - loss: 2.0367 - acc: 0.5217
Epoch 556/1000
- 0s - loss: 2.0357 - acc: 0.5217
Epoch 557/1000
- 0s - loss: 2.0351 - acc: 0.4783
Epoch 558/1000
- 0s - loss: 2.0340 - acc: 0.4783
Epoch 559/1000
- 0s - loss: 2.0329 - acc: 0.5652
Epoch 560/1000
- 0s - loss: 2.0324 - acc: 0.5652
Epoch 561/1000
- 0s - loss: 2.0316 - acc: 0.5217
Epoch 562/1000
- 0s - loss: 2.0308 - acc: 0.5217
Epoch 563/1000
- 0s - loss: 2.0296 - acc: 0.5217
Epoch 564/1000
- 0s - loss: 2.0288 - acc: 0.5217
Epoch 565/1000
- 0s - loss: 2.0272 - acc: 0.5217
Epoch 566/1000
- 0s - loss: 2.0271 - acc: 0.4783
Epoch 567/1000
- 0s - loss: 2.0262 - acc: 0.4348
Epoch 568/1000
- 0s - loss: 2.0248 - acc: 0.4348
Epoch 569/1000
- 0s - loss: 2.0243 - acc: 0.4783
Epoch 570/1000
- 0s - loss: 2.0235 - acc: 0.5217
Epoch 571/1000
- 0s - loss: 2.0224 - acc: 0.5217
Epoch 572/1000
- 0s - loss: 2.0214 - acc: 0.5217
Epoch 573/1000
- 0s - loss: 2.0212 - acc: 0.4783
Epoch 574/1000
- 0s - loss: 2.0197 - acc: 0.4783
Epoch 575/1000
- 0s - loss: 2.0192 - acc: 0.5217
Epoch 576/1000
- 0s - loss: 2.0186 - acc: 0.5217
Epoch 577/1000
- 0s - loss: 2.0175 - acc: 0.4783
Epoch 578/1000
- 0s - loss: 2.0164 - acc: 0.4783
Epoch 579/1000
- 0s - loss: 2.0155 - acc: 0.4348
Epoch 580/1000
- 0s - loss: 2.0142 - acc: 0.4348
Epoch 581/1000
- 0s - loss: 2.0139 - acc: 0.4783
Epoch 582/1000
- 0s - loss: 2.0128 - acc: 0.4783
Epoch 583/1000
- 0s - loss: 2.0121 - acc: 0.4783
Epoch 584/1000
- 0s - loss: 2.0109 - acc: 0.5217
Epoch 585/1000
- 0s - loss: 2.0109 - acc: 0.4783
Epoch 586/1000
- 0s - loss: 2.0092 - acc: 0.4783
Epoch 587/1000
- 0s - loss: 2.0086 - acc: 0.4348
Epoch 588/1000
- 0s - loss: 2.0086 - acc: 0.5217
Epoch 589/1000
- 0s - loss: 2.0069 - acc: 0.5217
Epoch 590/1000
- 0s - loss: 2.0059 - acc: 0.4783
Epoch 591/1000
- 0s - loss: 2.0048 - acc: 0.4783
Epoch 592/1000
- 0s - loss: 2.0052 - acc: 0.4348
Epoch 593/1000
- 0s - loss: 2.0037 - acc: 0.3913
Epoch 594/1000
- 0s - loss: 2.0030 - acc: 0.4348
Epoch 595/1000
- 0s - loss: 2.0018 - acc: 0.4348
Epoch 596/1000
- 0s - loss: 2.0010 - acc: 0.4348
Epoch 597/1000
- 0s - loss: 2.0008 - acc: 0.5217
Epoch 598/1000
- 0s - loss: 1.9992 - acc: 0.5217
Epoch 599/1000
- 0s - loss: 1.9989 - acc: 0.4783
Epoch 600/1000
- 0s - loss: 1.9977 - acc: 0.4348
Epoch 601/1000
- 0s - loss: 1.9977 - acc: 0.4783
Epoch 602/1000
- 0s - loss: 1.9965 - acc: 0.4783
Epoch 603/1000
- 0s - loss: 1.9963 - acc: 0.5217
Epoch 604/1000
- 0s - loss: 1.9944 - acc: 0.5217
Epoch 605/1000
- 0s - loss: 1.9944 - acc: 0.5217
Epoch 606/1000
- 0s - loss: 1.9932 - acc: 0.5217
Epoch 607/1000
- 0s - loss: 1.9923 - acc: 0.5652
Epoch 608/1000
- 0s - loss: 1.9916 - acc: 0.5652
Epoch 609/1000
- 0s - loss: 1.9903 - acc: 0.5217
Epoch 610/1000
- 0s - loss: 1.9894 - acc: 0.5652
Epoch 611/1000
- 0s - loss: 1.9904 - acc: 0.5652
Epoch 612/1000
- 0s - loss: 1.9887 - acc: 0.5217
Epoch 613/1000
- 0s - loss: 1.9882 - acc: 0.5217
Epoch 614/1000
- 0s - loss: 1.9866 - acc: 0.5652
Epoch 615/1000
- 0s - loss: 1.9864 - acc: 0.5652
Epoch 616/1000
- 0s - loss: 1.9860 - acc: 0.5652
Epoch 617/1000
- 0s - loss: 1.9850 - acc: 0.5652
Epoch 618/1000
- 0s - loss: 1.9840 - acc: 0.5652
Epoch 619/1000
- 0s - loss: 1.9833 - acc: 0.5652
Epoch 620/1000
- 0s - loss: 1.9828 - acc: 0.5652
Epoch 621/1000
- 0s - loss: 1.9816 - acc: 0.5652
Epoch 622/1000
- 0s - loss: 1.9811 - acc: 0.5217
Epoch 623/1000
- 0s - loss: 1.9803 - acc: 0.5652
Epoch 624/1000
- 0s - loss: 1.9790 - acc: 0.5217
Epoch 625/1000
- 0s - loss: 1.9780 - acc: 0.5217
Epoch 626/1000
- 0s - loss: 1.9784 - acc: 0.5217
Epoch 627/1000
- 0s - loss: 1.9765 - acc: 0.5217
Epoch 628/1000
- 0s - loss: 1.9759 - acc: 0.5217
Epoch 629/1000
- 0s - loss: 1.9754 - acc: 0.4783
Epoch 630/1000
- 0s - loss: 1.9745 - acc: 0.4783
Epoch 631/1000
- 0s - loss: 1.9744 - acc: 0.5217
Epoch 632/1000
- 0s - loss: 1.9726 - acc: 0.5217
Epoch 633/1000
- 0s - loss: 1.9718 - acc: 0.5217
Epoch 634/1000
- 0s - loss: 1.9712 - acc: 0.5217
Epoch 635/1000
- 0s - loss: 1.9702 - acc: 0.5217
Epoch 636/1000
- 0s - loss: 1.9701 - acc: 0.5217
Epoch 637/1000
- 0s - loss: 1.9690 - acc: 0.5217
Epoch 638/1000
- 0s - loss: 1.9686 - acc: 0.5217
Epoch 639/1000
- 0s - loss: 1.9680 - acc: 0.5652
Epoch 640/1000
- 0s - loss: 1.9667 - acc: 0.5217
Epoch 641/1000
- 0s - loss: 1.9663 - acc: 0.5217
Epoch 642/1000
- 0s - loss: 1.9652 - acc: 0.5652
Epoch 643/1000
- 0s - loss: 1.9646 - acc: 0.5652
Epoch 644/1000
- 0s - loss: 1.9638 - acc: 0.5217
Epoch 645/1000
- 0s - loss: 1.9632 - acc: 0.5652
Epoch 646/1000
- 0s - loss: 1.9622 - acc: 0.5652
Epoch 647/1000
- 0s - loss: 1.9619 - acc: 0.5652
Epoch 648/1000
- 0s - loss: 1.9605 - acc: 0.5652
Epoch 649/1000
- 0s - loss: 1.9607 - acc: 0.5217
Epoch 650/1000
- 0s - loss: 1.9586 - acc: 0.4783
Epoch 651/1000
- 0s - loss: 1.9589 - acc: 0.4783
Epoch 652/1000
- 0s - loss: 1.9573 - acc: 0.4348
Epoch 653/1000
- 0s - loss: 1.9573 - acc: 0.5217
Epoch 654/1000
- 0s - loss: 1.9571 - acc: 0.5217
Epoch 655/1000
- 0s - loss: 1.9556 - acc: 0.5652
Epoch 656/1000
- 0s - loss: 1.9545 - acc: 0.5217
Epoch 657/1000
- 0s - loss: 1.9543 - acc: 0.5217
Epoch 658/1000
- 0s - loss: 1.9543 - acc: 0.4783
Epoch 659/1000
- 0s - loss: 1.9529 - acc: 0.5652
Epoch 660/1000
- 0s - loss: 1.9521 - acc: 0.5652
Epoch 661/1000
- 0s - loss: 1.9511 - acc: 0.5217
Epoch 662/1000
- 0s - loss: 1.9504 - acc: 0.6087
Epoch 663/1000
- 0s - loss: 1.9493 - acc: 0.6087
Epoch 664/1000
- 0s - loss: 1.9492 - acc: 0.6087
Epoch 665/1000
- 0s - loss: 1.9488 - acc: 0.5652
Epoch 666/1000
- 0s - loss: 1.9474 - acc: 0.5217
Epoch 667/1000
- 0s - loss: 1.9467 - acc: 0.4783
Epoch 668/1000
- 0s - loss: 1.9457 - acc: 0.4783
Epoch 669/1000
- 0s - loss: 1.9451 - acc: 0.4783
Epoch 670/1000
- 0s - loss: 1.9440 - acc: 0.4783
Epoch 671/1000
- 0s - loss: 1.9443 - acc: 0.3913
Epoch 672/1000
- 0s - loss: 1.9431 - acc: 0.5217
Epoch 673/1000
- 0s - loss: 1.9421 - acc: 0.5217
Epoch 674/1000
- 0s - loss: 1.9412 - acc: 0.5217
Epoch 675/1000
- 0s - loss: 1.9410 - acc: 0.5217
Epoch 676/1000
- 0s - loss: 1.9401 - acc: 0.4783
Epoch 677/1000
- 0s - loss: 1.9392 - acc: 0.5217
Epoch 678/1000
- 0s - loss: 1.9390 - acc: 0.5652
Epoch 679/1000
- 0s - loss: 1.9385 - acc: 0.4783
Epoch 680/1000
- 0s - loss: 1.9369 - acc: 0.4783
Epoch 681/1000
- 0s - loss: 1.9367 - acc: 0.5217
Epoch 682/1000
- 0s - loss: 1.9356 - acc: 0.4783
Epoch 683/1000
- 0s - loss: 1.9348 - acc: 0.4348
Epoch 684/1000
- 0s - loss: 1.9347 - acc: 0.4783
Epoch 685/1000
- 0s - loss: 1.9337 - acc: 0.4783
Epoch 686/1000
- 0s - loss: 1.9332 - acc: 0.5217
Epoch 687/1000
- 0s - loss: 1.9322 - acc: 0.5217
Epoch 688/1000
- 0s - loss: 1.9316 - acc: 0.5217
Epoch 689/1000
- 0s - loss: 1.9304 - acc: 0.6087
Epoch 690/1000
- 0s - loss: 1.9302 - acc: 0.5652
Epoch 691/1000
- 0s - loss: 1.9303 - acc: 0.5652
Epoch 692/1000
- 0s - loss: 1.9289 - acc: 0.5217
Epoch 693/1000
- 0s - loss: 1.9283 - acc: 0.5217
Epoch 694/1000
- 0s - loss: 1.9279 - acc: 0.4783
Epoch 695/1000
- 0s - loss: 1.9264 - acc: 0.4783
Epoch 696/1000
- 0s - loss: 1.9262 - acc: 0.5217
Epoch 697/1000
- 0s - loss: 1.9251 - acc: 0.5217
Epoch 698/1000
- 0s - loss: 1.9245 - acc: 0.4783
Epoch 699/1000
- 0s - loss: 1.9236 - acc: 0.4783
Epoch 700/1000
- 0s - loss: 1.9231 - acc: 0.4783
Epoch 701/1000
- 0s - loss: 1.9227 - acc: 0.5217
Epoch 702/1000
- 0s - loss: 1.9214 - acc: 0.5217
Epoch 703/1000
- 0s - loss: 1.9203 - acc: 0.5217
Epoch 704/1000
- 0s - loss: 1.9208 - acc: 0.5217
Epoch 705/1000
- 0s - loss: 1.9194 - acc: 0.5217
Epoch 706/1000
- 0s - loss: 1.9194 - acc: 0.5217
Epoch 707/1000
- 0s - loss: 1.9185 - acc: 0.5217
Epoch 708/1000
- 0s - loss: 1.9172 - acc: 0.4783
Epoch 709/1000
- 0s - loss: 1.9171 - acc: 0.5217
Epoch 710/1000
- 0s - loss: 1.9154 - acc: 0.5652
Epoch 711/1000
- 0s - loss: 1.9153 - acc: 0.5652
Epoch 712/1000
- 0s - loss: 1.9151 - acc: 0.5652
Epoch 713/1000
- 0s - loss: 1.9141 - acc: 0.5652
Epoch 714/1000
- 0s - loss: 1.9139 - acc: 0.5652
Epoch 715/1000
- 0s - loss: 1.9134 - acc: 0.6087
Epoch 716/1000
- 0s - loss: 1.9132 - acc: 0.6087
Epoch 717/1000
- 0s - loss: 1.9114 - acc: 0.5652
Epoch 718/1000
- 0s - loss: 1.9112 - acc: 0.5652
Epoch 719/1000
- 0s - loss: 1.9106 - acc: 0.5652
Epoch 720/1000
- 0s - loss: 1.9098 - acc: 0.5217
Epoch 721/1000
- 0s - loss: 1.9093 - acc: 0.6087
Epoch 722/1000
- 0s - loss: 1.9093 - acc: 0.5217
Epoch 723/1000
- 0s - loss: 1.9075 - acc: 0.5217
Epoch 724/1000
- 0s - loss: 1.9066 - acc: 0.6087
Epoch 725/1000
- 0s - loss: 1.9064 - acc: 0.6087
Epoch 726/1000
- 0s - loss: 1.9062 - acc: 0.6087
Epoch 727/1000
- 0s - loss: 1.9051 - acc: 0.6522
Epoch 728/1000
- 0s - loss: 1.9043 - acc: 0.6522
Epoch 729/1000
- 0s - loss: 1.9032 - acc: 0.6522
Epoch 730/1000
- 0s - loss: 1.9031 - acc: 0.6522
Epoch 731/1000
- 0s - loss: 1.9023 - acc: 0.6522
Epoch 732/1000
- 0s - loss: 1.9012 - acc: 0.6522
Epoch 733/1000
- 0s - loss: 1.9008 - acc: 0.6087
Epoch 734/1000
- 0s - loss: 1.9000 - acc: 0.6087
Epoch 735/1000
- 0s - loss: 1.8994 - acc: 0.6522
Epoch 736/1000
- 0s - loss: 1.8992 - acc: 0.6522
Epoch 737/1000
- 0s - loss: 1.8985 - acc: 0.6522
Epoch 738/1000
- 0s - loss: 1.8976 - acc: 0.6522
Epoch 739/1000
- 0s - loss: 1.8973 - acc: 0.6087
Epoch 740/1000
- 0s - loss: 1.8952 - acc: 0.6087
Epoch 741/1000
- 0s - loss: 1.8955 - acc: 0.5652
Epoch 742/1000
- 0s - loss: 1.8949 - acc: 0.5217
Epoch 743/1000
- 0s - loss: 1.8940 - acc: 0.5217
Epoch 744/1000
- 0s - loss: 1.8938 - acc: 0.5217
Epoch 745/1000
- 0s - loss: 1.8930 - acc: 0.5217
Epoch 746/1000
- 0s - loss: 1.8921 - acc: 0.4783
Epoch 747/1000
- 0s - loss: 1.8921 - acc: 0.4783
Epoch 748/1000
- 0s - loss: 1.8911 - acc: 0.4783
Epoch 749/1000
- 0s - loss: 1.8902 - acc: 0.5217
Epoch 750/1000
- 0s - loss: 1.8893 - acc: 0.5652
Epoch 751/1000
- 0s - loss: 1.8895 - acc: 0.5652
Epoch 752/1000
- 0s - loss: 1.8886 - acc: 0.5652
Epoch 753/1000
- 0s - loss: 1.8882 - acc: 0.5652
Epoch 754/1000
- 0s - loss: 1.8871 - acc: 0.5652
Epoch 755/1000
- 0s - loss: 1.8872 - acc: 0.5652
Epoch 756/1000
- 0s - loss: 1.8865 - acc: 0.5652
Epoch 757/1000
- 0s - loss: 1.8859 - acc: 0.6087
Epoch 758/1000
- 0s - loss: 1.8841 - acc: 0.5652
Epoch 759/1000
- 0s - loss: 1.8840 - acc: 0.5217
Epoch 760/1000
- 0s - loss: 1.8832 - acc: 0.5217
Epoch 761/1000
- 0s - loss: 1.8830 - acc: 0.5217
Epoch 762/1000
- 0s - loss: 1.8814 - acc: 0.5217
Epoch 763/1000
- 0s - loss: 1.8818 - acc: 0.5217
Epoch 764/1000
- 0s - loss: 1.8811 - acc: 0.4783
Epoch 765/1000
- 0s - loss: 1.8808 - acc: 0.4783
Epoch 766/1000
- 0s - loss: 1.8803 - acc: 0.4783
Epoch 767/1000
- 0s - loss: 1.8791 - acc: 0.4783
Epoch 768/1000
- 0s - loss: 1.8785 - acc: 0.4783
Epoch 769/1000
- 0s - loss: 1.8778 - acc: 0.4783
Epoch 770/1000
- 0s - loss: 1.8767 - acc: 0.4783
Epoch 771/1000
- 0s - loss: 1.8768 - acc: 0.5217
Epoch 772/1000
- 0s - loss: 1.8763 - acc: 0.5217
Epoch 773/1000
- 0s - loss: 1.8758 - acc: 0.5652
Epoch 774/1000
- 0s - loss: 1.8746 - acc: 0.6087
Epoch 775/1000
- 0s - loss: 1.8738 - acc: 0.6087
Epoch 776/1000
- 0s - loss: 1.8737 - acc: 0.5652
Epoch 777/1000
- 0s - loss: 1.8731 - acc: 0.6087
Epoch 778/1000
- 0s - loss: 1.8720 - acc: 0.6087
Epoch 779/1000
- 0s - loss: 1.8718 - acc: 0.6087
Epoch 780/1000
- 0s - loss: 1.8712 - acc: 0.6522
Epoch 781/1000
- 0s - loss: 1.8703 - acc: 0.6087
Epoch 782/1000
- 0s - loss: 1.8698 - acc: 0.6522
Epoch 783/1000
- 0s - loss: 1.8688 - acc: 0.6522
Epoch 784/1000
- 0s - loss: 1.8681 - acc: 0.6522
Epoch 785/1000
- 0s - loss: 1.8677 - acc: 0.6522
Epoch 786/1000
- 0s - loss: 1.8668 - acc: 0.6522
Epoch 787/1000
- 0s - loss: 1.8661 - acc: 0.6522
Epoch 788/1000
- 0s - loss: 1.8653 - acc: 0.6522
Epoch 789/1000
- 0s - loss: 1.8651 - acc: 0.6522
Epoch 790/1000
- 0s - loss: 1.8649 - acc: 0.6087
Epoch 791/1000
- 0s - loss: 1.8644 - acc: 0.6087
Epoch 792/1000
- 0s - loss: 1.8628 - acc: 0.6522
Epoch 793/1000
- 0s - loss: 1.8625 - acc: 0.6522
Epoch 794/1000
- 0s - loss: 1.8624 - acc: 0.6087
Epoch 795/1000
- 0s - loss: 1.8621 - acc: 0.5652
Epoch 796/1000
- 0s - loss: 1.8610 - acc: 0.5217
Epoch 797/1000
- 0s - loss: 1.8601 - acc: 0.5652
Epoch 798/1000
- 0s - loss: 1.8592 - acc: 0.5217
Epoch 799/1000
- 0s - loss: 1.8583 - acc: 0.5652
Epoch 800/1000
- 0s - loss: 1.8575 - acc: 0.5652
Epoch 801/1000
- 0s - loss: 1.8568 - acc: 0.6087
Epoch 802/1000
- 0s - loss: 1.8575 - acc: 0.6087
Epoch 803/1000
- 0s - loss: 1.8568 - acc: 0.5652
Epoch 804/1000
- 0s - loss: 1.8560 - acc: 0.5652
Epoch 805/1000
- 0s - loss: 1.8554 - acc: 0.5652
Epoch 806/1000
- 0s - loss: 1.8547 - acc: 0.5652
Epoch 807/1000
- 0s - loss: 1.8549 - acc: 0.5217
Epoch 808/1000
- 0s - loss: 1.8532 - acc: 0.5217
Epoch 809/1000
- 0s - loss: 1.8533 - acc: 0.5652
Epoch 810/1000
- 0s - loss: 1.8526 - acc: 0.5217
Epoch 811/1000
- 0s - loss: 1.8517 - acc: 0.5217
Epoch 812/1000
- 0s - loss: 1.8509 - acc: 0.6087
Epoch 813/1000
- 0s - loss: 1.8508 - acc: 0.6087
Epoch 814/1000
- 0s - loss: 1.8507 - acc: 0.6087
Epoch 815/1000
- 0s - loss: 1.8493 - acc: 0.6522
Epoch 816/1000
- 0s - loss: 1.8486 - acc: 0.6087
Epoch 817/1000
- 0s - loss: 1.8482 - acc: 0.6087
Epoch 818/1000
- 0s - loss: 1.8471 - acc: 0.6087
Epoch 819/1000
- 0s - loss: 1.8472 - acc: 0.6522
Epoch 820/1000
- 0s - loss: 1.8463 - acc: 0.6522
Epoch 821/1000
- 0s - loss: 1.8453 - acc: 0.6957
Epoch 822/1000
- 0s - loss: 1.8462 - acc: 0.6957
Epoch 823/1000
- 0s - loss: 1.8444 - acc: 0.6957
Epoch 824/1000
- 0s - loss: 1.8432 - acc: 0.6522
Epoch 825/1000
- 0s - loss: 1.8428 - acc: 0.6522
Epoch 826/1000
- 0s - loss: 1.8431 - acc: 0.5217
Epoch 827/1000
- 0s - loss: 1.8427 - acc: 0.5217
Epoch 828/1000
- 0s - loss: 1.8416 - acc: 0.5652
Epoch 829/1000
- 0s - loss: 1.8404 - acc: 0.6087
Epoch 830/1000
- 0s - loss: 1.8397 - acc: 0.6087
Epoch 831/1000
- 0s - loss: 1.8404 - acc: 0.6087
Epoch 832/1000
- 0s - loss: 1.8392 - acc: 0.6087
Epoch 833/1000
- 0s - loss: 1.8382 - acc: 0.6522
Epoch 834/1000
- 0s - loss: 1.8382 - acc: 0.6087
Epoch 835/1000
- 0s - loss: 1.8373 - acc: 0.6522
Epoch 836/1000
- 0s - loss: 1.8370 - acc: 0.6087
Epoch 837/1000
- 0s - loss: 1.8364 - acc: 0.6087
Epoch 838/1000
- 0s - loss: 1.8356 - acc: 0.5652
Epoch 839/1000
- 0s - loss: 1.8356 - acc: 0.6087
Epoch 840/1000
- 0s - loss: 1.8341 - acc: 0.6522
Epoch 841/1000
- 0s - loss: 1.8336 - acc: 0.6522
Epoch 842/1000
- 0s - loss: 1.8339 - acc: 0.5652
Epoch 843/1000
- 0s - loss: 1.8329 - acc: 0.5652
Epoch 844/1000
- 0s - loss: 1.8320 - acc: 0.5652
Epoch 845/1000
- 0s - loss: 1.8314 - acc: 0.6087
Epoch 846/1000
- 0s - loss: 1.8317 - acc: 0.5652
Epoch 847/1000
- 0s - loss: 1.8308 - acc: 0.6087
Epoch 848/1000
- 0s - loss: 1.8296 - acc: 0.5652
Epoch 849/1000
- 0s - loss: 1.8292 - acc: 0.5652
Epoch 850/1000
- 0s - loss: 1.8291 - acc: 0.5217
Epoch 851/1000
- 0s - loss: 1.8282 - acc: 0.5652
Epoch 852/1000
- 0s - loss: 1.8274 - acc: 0.5652
Epoch 853/1000
- 0s - loss: 1.8273 - acc: 0.5217
Epoch 854/1000
- 0s - loss: 1.8261 - acc: 0.5217
Epoch 855/1000
- 0s - loss: 1.8251 - acc: 0.5217
Epoch 856/1000
- 0s - loss: 1.8253 - acc: 0.5652
Epoch 857/1000
- 0s - loss: 1.8255 - acc: 0.5652
Epoch 858/1000
- 0s - loss: 1.8241 - acc: 0.5217
Epoch 859/1000
- 0s - loss: 1.8241 - acc: 0.5652
Epoch 860/1000
- 0s - loss: 1.8235 - acc: 0.5217
Epoch 861/1000
- 0s - loss: 1.8231 - acc: 0.5652
Epoch 862/1000
- 0s - loss: 1.8218 - acc: 0.6522
Epoch 863/1000
- 0s - loss: 1.8218 - acc: 0.6087
Epoch 864/1000
- 0s - loss: 1.8212 - acc: 0.5652
Epoch 865/1000
- 0s - loss: 1.8201 - acc: 0.6522
Epoch 866/1000
- 0s - loss: 1.8199 - acc: 0.6522
Epoch 867/1000
- 0s - loss: 1.8194 - acc: 0.6087
Epoch 868/1000
- 0s - loss: 1.8191 - acc: 0.6087
Epoch 869/1000
- 0s - loss: 1.8187 - acc: 0.6087
Epoch 870/1000
- 0s - loss: 1.8175 - acc: 0.5652
Epoch 871/1000
- 0s - loss: 1.8171 - acc: 0.5217
Epoch 872/1000
- 0s - loss: 1.8171 - acc: 0.5217
Epoch 873/1000
- 0s - loss: 1.8157 - acc: 0.4783
Epoch 874/1000
- 0s - loss: 1.8148 - acc: 0.5652
Epoch 875/1000
- 0s - loss: 1.8137 - acc: 0.5652
Epoch 876/1000
- 0s - loss: 1.8136 - acc: 0.6522
Epoch 877/1000
- 0s - loss: 1.8134 - acc: 0.6522
Epoch 878/1000
- 0s - loss: 1.8133 - acc: 0.7391
Epoch 879/1000
- 0s - loss: 1.8125 - acc: 0.6957
Epoch 880/1000
- 0s - loss: 1.8116 - acc: 0.6522
Epoch 881/1000
- 0s - loss: 1.8112 - acc: 0.6522
Epoch 882/1000
- 0s - loss: 1.8099 - acc: 0.6957
Epoch 883/1000
- 0s - loss: 1.8102 - acc: 0.6522
Epoch 884/1000
- 0s - loss: 1.8099 - acc: 0.6522
Epoch 885/1000
- 0s - loss: 1.8087 - acc: 0.6522
Epoch 886/1000
- 0s - loss: 1.8087 - acc: 0.5652
Epoch 887/1000
- 0s - loss: 1.8071 - acc: 0.5652
Epoch 888/1000
- 0s - loss: 1.8074 - acc: 0.5652
Epoch 889/1000
- 0s - loss: 1.8069 - acc: 0.5652
Epoch 890/1000
- 0s - loss: 1.8064 - acc: 0.6087
Epoch 891/1000
- 0s - loss: 1.8054 - acc: 0.6087
Epoch 892/1000
- 0s - loss: 1.8052 - acc: 0.6087
Epoch 893/1000
- 0s - loss: 1.8042 - acc: 0.6522
Epoch 894/1000
- 0s - loss: 1.8048 - acc: 0.6087
Epoch 895/1000
- 0s - loss: 1.8033 - acc: 0.6087
Epoch 896/1000
- 0s - loss: 1.8028 - acc: 0.5652
Epoch 897/1000
- 0s - loss: 1.8021 - acc: 0.6087
Epoch 898/1000
- 0s - loss: 1.8022 - acc: 0.5652
Epoch 899/1000
- 0s - loss: 1.8022 - acc: 0.5652
Epoch 900/1000
- 0s - loss: 1.8014 - acc: 0.5652
Epoch 901/1000
- 0s - loss: 1.8007 - acc: 0.5652
Epoch 902/1000
- 0s - loss: 1.7994 - acc: 0.5652
Epoch 903/1000
- 0s - loss: 1.7994 - acc: 0.5652
Epoch 904/1000
- 0s - loss: 1.7984 - acc: 0.6087
Epoch 905/1000
- 0s - loss: 1.7982 - acc: 0.6522
Epoch 906/1000
- 0s - loss: 1.7973 - acc: 0.6087
Epoch 907/1000
- 0s - loss: 1.7978 - acc: 0.6087
Epoch 908/1000
- 0s - loss: 1.7968 - acc: 0.6087
Epoch 909/1000
- 0s - loss: 1.7964 - acc: 0.6087
Epoch 910/1000
- 0s - loss: 1.7956 - acc: 0.5652
Epoch 911/1000
- 0s - loss: 1.7947 - acc: 0.5652
Epoch 912/1000
- 0s - loss: 1.7943 - acc: 0.6087
Epoch 913/1000
- 0s - loss: 1.7944 - acc: 0.6087
Epoch 914/1000
- 0s - loss: 1.7934 - acc: 0.5652
Epoch 915/1000
- 0s - loss: 1.7927 - acc: 0.6087
Epoch 916/1000
- 0s - loss: 1.7922 - acc: 0.6087
Epoch 917/1000
- 0s - loss: 1.7919 - acc: 0.6087
Epoch 918/1000
- 0s - loss: 1.7909 - acc: 0.6087
Epoch 919/1000
- 0s - loss: 1.7913 - acc: 0.5217
Epoch 920/1000
- 0s - loss: 1.7903 - acc: 0.6087
Epoch 921/1000
- 0s - loss: 1.7897 - acc: 0.6087
Epoch 922/1000
- 0s - loss: 1.7886 - acc: 0.6087
Epoch 923/1000
- 0s - loss: 1.7891 - acc: 0.6087
Epoch 924/1000
- 0s - loss: 1.7870 - acc: 0.6522
Epoch 925/1000
- 0s - loss: 1.7870 - acc: 0.6522
Epoch 926/1000
- 0s - loss: 1.7861 - acc: 0.6522
Epoch 927/1000
- 0s - loss: 1.7861 - acc: 0.6957
Epoch 928/1000
- 0s - loss: 1.7856 - acc: 0.6957
Epoch 929/1000
- 0s - loss: 1.7852 - acc: 0.6522
Epoch 930/1000
- 0s - loss: 1.7856 - acc: 0.6522
Epoch 931/1000
- 0s - loss: 1.7840 - acc: 0.6522
Epoch 932/1000
- 0s - loss: 1.7840 - acc: 0.6957
Epoch 933/1000
- 0s - loss: 1.7834 - acc: 0.6957
Epoch 934/1000
- 0s - loss: 1.7832 - acc: 0.6522
Epoch 935/1000
- 0s - loss: 1.7822 - acc: 0.6957
Epoch 936/1000
- 0s - loss: 1.7821 - acc: 0.6522
Epoch 937/1000
- 0s - loss: 1.7808 - acc: 0.6522
Epoch 938/1000
- 0s - loss: 1.7805 - acc: 0.6522
Epoch 939/1000
- 0s - loss: 1.7796 - acc: 0.7391
Epoch 940/1000
- 0s - loss: 1.7790 - acc: 0.7391
Epoch 941/1000
- 0s - loss: 1.7787 - acc: 0.6522
Epoch 942/1000
- 0s - loss: 1.7784 - acc: 0.7391
Epoch 943/1000
- 0s - loss: 1.7779 - acc: 0.6957
Epoch 944/1000
- 0s - loss: 1.7772 - acc: 0.6957
Epoch 945/1000
- 0s - loss: 1.7769 - acc: 0.6957
Epoch 946/1000
- 0s - loss: 1.7760 - acc: 0.6522
Epoch 947/1000
- 0s - loss: 1.7766 - acc: 0.6957
Epoch 948/1000
- 0s - loss: 1.7749 - acc: 0.6522
Epoch 949/1000
- 0s - loss: 1.7745 - acc: 0.6522
Epoch 950/1000
- 0s - loss: 1.7748 - acc: 0.6957
Epoch 951/1000
- 0s - loss: 1.7730 - acc: 0.6522
Epoch 952/1000
- 0s - loss: 1.7734 - acc: 0.5652
Epoch 953/1000
- 0s - loss: 1.7725 - acc: 0.6087
Epoch 954/1000
- 0s - loss: 1.7718 - acc: 0.6087
Epoch 955/1000
- 0s - loss: 1.7728 - acc: 0.6087
Epoch 956/1000
- 0s - loss: 1.7713 - acc: 0.6087
Epoch 957/1000
- 0s - loss: 1.7707 - acc: 0.5652
Epoch 958/1000
- 0s - loss: 1.7706 - acc: 0.6087
Epoch 959/1000
- 0s - loss: 1.7696 - acc: 0.6522
Epoch 960/1000
- 0s - loss: 1.7690 - acc: 0.6087
Epoch 961/1000
- 0s - loss: 1.7688 - acc: 0.5652
Epoch 962/1000
- 0s - loss: 1.7673 - acc: 0.6522
Epoch 963/1000
- 0s - loss: 1.7678 - acc: 0.6087
Epoch 964/1000
- 0s - loss: 1.7671 - acc: 0.6087
Epoch 965/1000
- 0s - loss: 1.7667 - acc: 0.5652
Epoch 966/1000
- 0s - loss: 1.7664 - acc: 0.5217
Epoch 967/1000
- 0s - loss: 1.7659 - acc: 0.5652
Epoch 968/1000
- 0s - loss: 1.7644 - acc: 0.6087
Epoch 969/1000
- 0s - loss: 1.7646 - acc: 0.6087
Epoch 970/1000
- 0s - loss: 1.7644 - acc: 0.6087
Epoch 971/1000
- 0s - loss: 1.7636 - acc: 0.6522
Epoch 972/1000
- 0s - loss: 1.7639 - acc: 0.6522
Epoch 973/1000
- 0s - loss: 1.7617 - acc: 0.6957
Epoch 974/1000
- 0s - loss: 1.7617 - acc: 0.6522
Epoch 975/1000
- 0s - loss: 1.7611 - acc: 0.6087
Epoch 976/1000
- 0s - loss: 1.7614 - acc: 0.6087
Epoch 977/1000
- 0s - loss: 1.7602 - acc: 0.6957
Epoch 978/1000
- 0s - loss: 1.7605 - acc: 0.6957
Epoch 979/1000
- 0s - loss: 1.7598 - acc: 0.6522
Epoch 980/1000
- 0s - loss: 1.7588 - acc: 0.6522
Epoch 981/1000
- 0s - loss: 1.7583 - acc: 0.6522
Epoch 982/1000
- 0s - loss: 1.7577 - acc: 0.6522
Epoch 983/1000
- 0s - loss: 1.7579 - acc: 0.6087
Epoch 984/1000
- 0s - loss: 1.7574 - acc: 0.6087
Epoch 985/1000
- 0s - loss: 1.7561 - acc: 0.6522
Epoch 986/1000
- 0s - loss: 1.7561 - acc: 0.6522
Epoch 987/1000
- 0s - loss: 1.7550 - acc: 0.6087
Epoch 988/1000
- 0s - loss: 1.7547 - acc: 0.5652
Epoch 989/1000
- 0s - loss: 1.7539 - acc: 0.6087
Epoch 990/1000
- 0s - loss: 1.7542 - acc: 0.6087
Epoch 991/1000
- 0s - loss: 1.7530 - acc: 0.6522
Epoch 992/1000
- 0s - loss: 1.7538 - acc: 0.6087
Epoch 993/1000
- 0s - loss: 1.7528 - acc: 0.6087
Epoch 994/1000
- 0s - loss: 1.7521 - acc: 0.6087
Epoch 995/1000
- 0s - loss: 1.7516 - acc: 0.6522
Epoch 996/1000
- 0s - loss: 1.7516 - acc: 0.6522
Epoch 997/1000
- 0s - loss: 1.7500 - acc: 0.6957
Epoch 998/1000
- 0s - loss: 1.7493 - acc: 0.6522
Epoch 999/1000
- 0s - loss: 1.7490 - acc: 0.6957
Epoch 1000/1000
- 0s - loss: 1.7488 - acc: 0.6522
23/23 [==============================] - 0s 9ms/step
Model Accuracy: 0.70
['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> L
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> Q
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> T
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> V
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> X
['U', 'V', 'W'] -> Z
['V', 'W', 'X'] -> Z
['W', 'X', 'Y'] -> Z
X.shape[1], y.shape[1] # get a sense of the shapes to understand the network architecture
The network does learn, and could be trained to get a good accuracy. But what's really going on here?
Let's leave aside for a moment the simplistic training data (one fun experiment would be to create corrupted sequences and augment the data with those, forcing the network to pay attention to the whole sequence).
Because the model is fundamentally symmetric and stateless (in terms of the sequence; naturally it has weights), this model would need to learn every sequential feature relative to every single sequence position. That seems difficult, inflexible, and inefficient.
Maybe we could add layers, neurons, and extra connections to mitigate parts of the problem. We could also do things like a 1D convolution to pick up frequencies and some patterns.
But instead, it might make more sense to explicitly model the sequential nature of the data (a bit like how we explictly modeled the 2D nature of image data with CNNs).
Recurrent Neural Network Concept
Let's take the neuron's output from one time (t) and feed it into that same neuron at a later time (t+1), in combination with other relevant inputs. Then we would have a neuron with memory.
We can weight the "return" of that value and train the weight -- so the neuron learns how important the previous value is relative to the current one.
Different neurons might learn to "remember" different amounts of prior history.
This concept is called a Recurrent Neural Network, originally developed around the 1980s.
Let's recall some pointers from the crash intro to Deep learning.
Watch following videos now for 12 minutes for the fastest introduction to RNNs and LSTMs
Udacity: Deep Learning by Vincent Vanhoucke - Recurrent Neural network
Recurrent neural network
 http://colah.github.io/posts/2015-08-Understanding-LSTMs/
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
http://karpathy.github.io/2015/05/21/rnn-effectiveness/ ***
LSTM - Long short term memory

GRU - Gated recurrent unit
 http://arxiv.org/pdf/1406.1078v3.pdf
http://arxiv.org/pdf/1406.1078v3.pdf
Training a Recurrent Neural Network

We can train an RNN using backpropagation with a minor twist: since RNN neurons with different states over time can be "unrolled" (i.e., are analogous) to a sequence of neurons with the "remember" weight linking directly forward from (t) to (t+1), we can backpropagate through time as well as the physical layers of the network.
This is, in fact, called Backpropagation Through Time (BPTT)
The idea is sound but -- since it creates patterns similar to very deep networks -- it suffers from the same challenges: * Vanishing gradient * Exploding gradient * Saturation * etc.
i.e., many of the same problems with early deep feed-forward networks having lots of weights.
10 steps back in time for a single layer is a not as bad as 10 layers (since there are fewer connections and, hence, weights) but it does get expensive.
ASIDE: Hierarchical and Recursive Networks, Bidirectional RNN
Network topologies can be built to reflect the relative structure of the data we are modeling. E.g., for natural language, grammar constraints mean that both hierarchy and (limited) recursion may allow a physically smaller model to achieve more effective capacity.
A bi-directional RNN includes values from previous and subsequent time steps. This is less strange than it sounds at first: after all, in many problems, such as sentence translation (where BiRNNs are very popular) we usually have the entire source sequence at one time. In that case, a BiDiRNN is really just saying that both prior and subsequent words can influence the interpretation of each word, something we humans take for granted.
Recent versions of neural net libraries have support for bidirectional networks, although you may need to write (or locate) a little code yourself if you want to experiment with hierarchical networks.
Long Short-Term Memory (LSTM)
"Pure" RNNs were never very successful. Sepp Hochreiter and Jürgen Schmidhuber (1997) made a game-changing contribution with the publication of the Long Short-Term Memory unit. How game changing? It's effectively state of the art today.
(Credit and much thanks to Chris Olah, http://colah.github.io/about.html, Research Scientist at Google Brain, for publishing the following excellent diagrams!)
*In the following diagrams, pay close attention that the output value is "split" for graphical purposes -- so the two *h* arrows/signals coming out are the same signal.*
RNN Cell: 
LSTM Cell:

An LSTM unit is a neuron with some bonus features: * Cell state propagated across time * Input, Output, Forget gates * Learns retention/discard of cell state * Admixture of new data * Output partly distinct from state * Use of addition (not multiplication) to combine input and cell state allows state to propagate unimpeded across time (addition of gradient)
ASIDE: Variations on LSTM
... include "peephole" where gate functions have direct access to cell state; convolutional; and bidirectional, where we can "cheat" by letting neurons learn from future time steps and not just previous time steps.
Slow down ... exactly what's getting added to where? For a step-by-step walk through, read Chris Olah's full post http://colah.github.io/posts/2015-08-Understanding-LSTMs/
Do LSTMs Work Reasonably Well?
Yes! These architectures are in production (2017) for deep-learning-enabled products at Baidu, Google, Microsoft, Apple, and elsewhere. They are used to solve problems in time series analysis, speech recognition and generation, connected handwriting, grammar, music, and robot control systems.
Let's Code an LSTM Variant of our Sequence Lab
(this great demo example courtesy of Jason Brownlee: http://machinelearningmastery.com/understanding-stateful-lstm-recurrent-neural-networks-python-keras/)
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.utils import np_utils
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print (seq_in, '->', seq_out)
# reshape X to be .......[samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))
X = X / float(len(alphabet))
y = np_utils.to_categorical(dataY)
# Let’s define an LSTM network with 32 units and an output layer with a softmax activation function for making predictions.
# a naive implementation of LSTM
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2]))) # <- LSTM layer...
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=400, batch_size=1, verbose=2)
scores = model.evaluate(X, y)
print("Model Accuracy: %.2f%%" % (scores[1]*100))
for pattern in dataX:
x = numpy.reshape(pattern, (1, len(pattern), 1))
x = x / float(len(alphabet))
prediction = model.predict(x, verbose=0)
index = numpy.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
print (seq_in, "->", result)
ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z
Epoch 1/400
- 4s - loss: 3.2653 - acc: 0.0000e+00
Epoch 2/400
- 0s - loss: 3.2498 - acc: 0.0000e+00
Epoch 3/400
- 0s - loss: 3.2411 - acc: 0.0000e+00
Epoch 4/400
- 0s - loss: 3.2330 - acc: 0.0435
Epoch 5/400
- 0s - loss: 3.2242 - acc: 0.0435
Epoch 6/400
- 0s - loss: 3.2152 - acc: 0.0435
Epoch 7/400
- 0s - loss: 3.2046 - acc: 0.0435
Epoch 8/400
- 0s - loss: 3.1946 - acc: 0.0435
Epoch 9/400
- 0s - loss: 3.1835 - acc: 0.0435
Epoch 10/400
- 0s - loss: 3.1720 - acc: 0.0435
Epoch 11/400
- 0s - loss: 3.1583 - acc: 0.0435
Epoch 12/400
- 0s - loss: 3.1464 - acc: 0.0435
Epoch 13/400
- 0s - loss: 3.1316 - acc: 0.0435
Epoch 14/400
- 0s - loss: 3.1176 - acc: 0.0435
Epoch 15/400
- 0s - loss: 3.1036 - acc: 0.0435
Epoch 16/400
- 0s - loss: 3.0906 - acc: 0.0435
Epoch 17/400
- 0s - loss: 3.0775 - acc: 0.0435
Epoch 18/400
- 0s - loss: 3.0652 - acc: 0.0435
Epoch 19/400
- 0s - loss: 3.0515 - acc: 0.0435
Epoch 20/400
- 0s - loss: 3.0388 - acc: 0.0435
Epoch 21/400
- 0s - loss: 3.0213 - acc: 0.0435
Epoch 22/400
- 0s - loss: 3.0044 - acc: 0.0435
Epoch 23/400
- 0s - loss: 2.9900 - acc: 0.1304
Epoch 24/400
- 0s - loss: 2.9682 - acc: 0.0870
Epoch 25/400
- 0s - loss: 2.9448 - acc: 0.0870
Epoch 26/400
- 0s - loss: 2.9237 - acc: 0.0870
Epoch 27/400
- 0s - loss: 2.8948 - acc: 0.0870
Epoch 28/400
- 0s - loss: 2.8681 - acc: 0.0870
Epoch 29/400
- 0s - loss: 2.8377 - acc: 0.0435
Epoch 30/400
- 0s - loss: 2.8008 - acc: 0.0870
Epoch 31/400
- 0s - loss: 2.7691 - acc: 0.0435
Epoch 32/400
- 0s - loss: 2.7268 - acc: 0.0870
Epoch 33/400
- 0s - loss: 2.6963 - acc: 0.0870
Epoch 34/400
- 0s - loss: 2.6602 - acc: 0.0870
Epoch 35/400
- 0s - loss: 2.6285 - acc: 0.1304
Epoch 36/400
- 0s - loss: 2.5979 - acc: 0.0870
Epoch 37/400
- 0s - loss: 2.5701 - acc: 0.1304
Epoch 38/400
- 0s - loss: 2.5443 - acc: 0.0870
Epoch 39/400
- 0s - loss: 2.5176 - acc: 0.0870
Epoch 40/400
- 0s - loss: 2.4962 - acc: 0.0870
Epoch 41/400
- 0s - loss: 2.4737 - acc: 0.0870
Epoch 42/400
- 0s - loss: 2.4496 - acc: 0.1739
Epoch 43/400
- 0s - loss: 2.4295 - acc: 0.1304
Epoch 44/400
- 0s - loss: 2.4045 - acc: 0.1739
Epoch 45/400
- 0s - loss: 2.3876 - acc: 0.1739
Epoch 46/400
- 0s - loss: 2.3671 - acc: 0.1739
Epoch 47/400
- 0s - loss: 2.3512 - acc: 0.1739
Epoch 48/400
- 0s - loss: 2.3301 - acc: 0.1739
Epoch 49/400
- 0s - loss: 2.3083 - acc: 0.1739
Epoch 50/400
- 0s - loss: 2.2833 - acc: 0.1739
Epoch 51/400
- 0s - loss: 2.2715 - acc: 0.1739
Epoch 52/400
- 0s - loss: 2.2451 - acc: 0.2174
Epoch 53/400
- 0s - loss: 2.2219 - acc: 0.2174
Epoch 54/400
- 0s - loss: 2.2025 - acc: 0.1304
Epoch 55/400
- 0s - loss: 2.1868 - acc: 0.2174
Epoch 56/400
- 0s - loss: 2.1606 - acc: 0.2174
Epoch 57/400
- 0s - loss: 2.1392 - acc: 0.2609
Epoch 58/400
- 0s - loss: 2.1255 - acc: 0.1739
Epoch 59/400
- 0s - loss: 2.1084 - acc: 0.2609
Epoch 60/400
- 0s - loss: 2.0835 - acc: 0.2609
Epoch 61/400
- 0s - loss: 2.0728 - acc: 0.2609
Epoch 62/400
- 0s - loss: 2.0531 - acc: 0.2174
Epoch 63/400
- 0s - loss: 2.0257 - acc: 0.2174
Epoch 64/400
- 0s - loss: 2.0192 - acc: 0.2174
Epoch 65/400
- 0s - loss: 1.9978 - acc: 0.2609
Epoch 66/400
- 0s - loss: 1.9792 - acc: 0.1304
Epoch 67/400
- 0s - loss: 1.9655 - acc: 0.3478
Epoch 68/400
- 0s - loss: 1.9523 - acc: 0.2609
Epoch 69/400
- 0s - loss: 1.9402 - acc: 0.2609
Epoch 70/400
- 0s - loss: 1.9220 - acc: 0.3043
Epoch 71/400
- 0s - loss: 1.9075 - acc: 0.2609
Epoch 72/400
- 0s - loss: 1.8899 - acc: 0.3913
Epoch 73/400
- 0s - loss: 1.8829 - acc: 0.3043
Epoch 74/400
- 0s - loss: 1.8569 - acc: 0.2174
Epoch 75/400
- 0s - loss: 1.8435 - acc: 0.3043
Epoch 76/400
- 0s - loss: 1.8361 - acc: 0.3043
Epoch 77/400
- 0s - loss: 1.8228 - acc: 0.3478
Epoch 78/400
- 0s - loss: 1.8145 - acc: 0.3043
Epoch 79/400
- 0s - loss: 1.7982 - acc: 0.3913
Epoch 80/400
- 0s - loss: 1.7836 - acc: 0.3913
Epoch 81/400
- 0s - loss: 1.7795 - acc: 0.4348
Epoch 82/400
- 0s - loss: 1.7646 - acc: 0.4783
Epoch 83/400
- 0s - loss: 1.7487 - acc: 0.4348
Epoch 84/400
- 0s - loss: 1.7348 - acc: 0.4348
Epoch 85/400
- 0s - loss: 1.7249 - acc: 0.5217
Epoch 86/400
- 0s - loss: 1.7153 - acc: 0.4348
Epoch 87/400
- 0s - loss: 1.7095 - acc: 0.4348
Epoch 88/400
- 0s - loss: 1.6938 - acc: 0.4348
Epoch 89/400
- 0s - loss: 1.6849 - acc: 0.5217
Epoch 90/400
- 0s - loss: 1.6712 - acc: 0.4348
Epoch 91/400
- 0s - loss: 1.6617 - acc: 0.5652
Epoch 92/400
- 0s - loss: 1.6531 - acc: 0.4348
Epoch 93/400
- 0s - loss: 1.6459 - acc: 0.5217
Epoch 94/400
- 0s - loss: 1.6341 - acc: 0.4783
Epoch 95/400
- 0s - loss: 1.6289 - acc: 0.5652
Epoch 96/400
- 0s - loss: 1.6138 - acc: 0.4783
Epoch 97/400
- 0s - loss: 1.6042 - acc: 0.4348
Epoch 98/400
- 0s - loss: 1.5907 - acc: 0.5652
Epoch 99/400
- 0s - loss: 1.5868 - acc: 0.4783
Epoch 100/400
- 0s - loss: 1.5756 - acc: 0.5217
Epoch 101/400
- 0s - loss: 1.5681 - acc: 0.5652
Epoch 102/400
- 0s - loss: 1.5582 - acc: 0.5652
Epoch 103/400
- 0s - loss: 1.5478 - acc: 0.6087
Epoch 104/400
- 0s - loss: 1.5375 - acc: 0.6087
Epoch 105/400
- 0s - loss: 1.5340 - acc: 0.6522
Epoch 106/400
- 0s - loss: 1.5175 - acc: 0.6522
Epoch 107/400
- 0s - loss: 1.5127 - acc: 0.5652
Epoch 108/400
- 0s - loss: 1.5207 - acc: 0.5652
Epoch 109/400
- 0s - loss: 1.5064 - acc: 0.5652
Epoch 110/400
- 0s - loss: 1.4968 - acc: 0.5652
Epoch 111/400
- 0s - loss: 1.4843 - acc: 0.6522
Epoch 112/400
- 0s - loss: 1.4806 - acc: 0.5217
Epoch 113/400
- 0s - loss: 1.4702 - acc: 0.7826
Epoch 114/400
- 0s - loss: 1.4555 - acc: 0.6957
Epoch 115/400
- 0s - loss: 1.4459 - acc: 0.6087
Epoch 116/400
- 0s - loss: 1.4542 - acc: 0.6522
Epoch 117/400
- 0s - loss: 1.4375 - acc: 0.7391
Epoch 118/400
- 0s - loss: 1.4328 - acc: 0.7391
Epoch 119/400
- 0s - loss: 1.4338 - acc: 0.7826
Epoch 120/400
- 0s - loss: 1.4155 - acc: 0.6087
Epoch 121/400
- 0s - loss: 1.4043 - acc: 0.6957
Epoch 122/400
- 0s - loss: 1.4009 - acc: 0.7391
Epoch 123/400
- 0s - loss: 1.3980 - acc: 0.7391
Epoch 124/400
- 0s - loss: 1.3869 - acc: 0.6957
Epoch 125/400
- 0s - loss: 1.3837 - acc: 0.6522
Epoch 126/400
- 0s - loss: 1.3753 - acc: 0.7826
Epoch 127/400
- 0s - loss: 1.3670 - acc: 0.7391
Epoch 128/400
- 0s - loss: 1.3586 - acc: 0.7826
Epoch 129/400
- 0s - loss: 1.3564 - acc: 0.6957
Epoch 130/400
- 0s - loss: 1.3448 - acc: 0.6957
Epoch 131/400
- 0s - loss: 1.3371 - acc: 0.8261
Epoch 132/400
- 0s - loss: 1.3330 - acc: 0.6957
Epoch 133/400
- 0s - loss: 1.3353 - acc: 0.6957
Epoch 134/400
- 0s - loss: 1.3239 - acc: 0.7391
Epoch 135/400
- 0s - loss: 1.3152 - acc: 0.8696
Epoch 136/400
- 0s - loss: 1.3186 - acc: 0.7391
Epoch 137/400
- 0s - loss: 1.3026 - acc: 0.8261
Epoch 138/400
- 0s - loss: 1.2946 - acc: 0.8696
Epoch 139/400
- 0s - loss: 1.2903 - acc: 0.7826
Epoch 140/400
- 0s - loss: 1.2894 - acc: 0.7391
Epoch 141/400
- 0s - loss: 1.2887 - acc: 0.7826
Epoch 142/400
- 0s - loss: 1.2733 - acc: 0.7826
Epoch 143/400
- 0s - loss: 1.2709 - acc: 0.7826
Epoch 144/400
- 0s - loss: 1.2638 - acc: 0.7826
Epoch 145/400
- 0s - loss: 1.2636 - acc: 0.8261
Epoch 146/400
- 0s - loss: 1.2513 - acc: 0.8261
Epoch 147/400
- 0s - loss: 1.2459 - acc: 0.7826
Epoch 148/400
- 0s - loss: 1.2422 - acc: 0.8696
Epoch 149/400
- 0s - loss: 1.2354 - acc: 0.8696
Epoch 150/400
- 0s - loss: 1.2265 - acc: 0.7826
Epoch 151/400
- 0s - loss: 1.2295 - acc: 0.8696
Epoch 152/400
- 0s - loss: 1.2192 - acc: 0.8696
Epoch 153/400
- 0s - loss: 1.2146 - acc: 0.8261
Epoch 154/400
- 0s - loss: 1.2152 - acc: 0.7826
Epoch 155/400
- 0s - loss: 1.2052 - acc: 0.7826
Epoch 156/400
- 0s - loss: 1.1943 - acc: 0.9565
Epoch 157/400
- 0s - loss: 1.1902 - acc: 0.8696
Epoch 158/400
- 0s - loss: 1.1877 - acc: 0.8696
Epoch 159/400
- 0s - loss: 1.1822 - acc: 0.8696
Epoch 160/400
- 0s - loss: 1.1718 - acc: 0.8261
Epoch 161/400
- 0s - loss: 1.1740 - acc: 0.8696
Epoch 162/400
- 0s - loss: 1.1696 - acc: 0.8696
Epoch 163/400
- 0s - loss: 1.1593 - acc: 0.8261
Epoch 164/400
- 0s - loss: 1.1580 - acc: 0.8696
Epoch 165/400
- 0s - loss: 1.1519 - acc: 0.9130
Epoch 166/400
- 0s - loss: 1.1453 - acc: 0.8696
Epoch 167/400
- 0s - loss: 1.1479 - acc: 0.7826
Epoch 168/400
- 0s - loss: 1.1391 - acc: 0.7826
Epoch 169/400
- 0s - loss: 1.1348 - acc: 0.8261
Epoch 170/400
- 0s - loss: 1.1261 - acc: 0.8696
Epoch 171/400
- 0s - loss: 1.1268 - acc: 0.8261
Epoch 172/400
- 0s - loss: 1.1216 - acc: 0.7826
Epoch 173/400
- 0s - loss: 1.1119 - acc: 0.9130
Epoch 174/400
- 0s - loss: 1.1071 - acc: 0.9130
Epoch 175/400
- 0s - loss: 1.0984 - acc: 0.9130
Epoch 176/400
- 0s - loss: 1.0921 - acc: 0.9565
Epoch 177/400
- 0s - loss: 1.0938 - acc: 0.8696
Epoch 178/400
- 0s - loss: 1.0904 - acc: 0.8261
Epoch 179/400
- 0s - loss: 1.0905 - acc: 0.8696
Epoch 180/400
- 0s - loss: 1.0749 - acc: 0.9565
Epoch 181/400
- 0s - loss: 1.0749 - acc: 0.8261
Epoch 182/400
- 0s - loss: 1.0705 - acc: 0.9130
Epoch 183/400
- 0s - loss: 1.0686 - acc: 0.8696
Epoch 184/400
- 0s - loss: 1.0553 - acc: 0.9130
Epoch 185/400
- 0s - loss: 1.0552 - acc: 0.8696
Epoch 186/400
- 0s - loss: 1.0593 - acc: 0.9130
Epoch 187/400
- 0s - loss: 1.0508 - acc: 0.8261
Epoch 188/400
- 0s - loss: 1.0453 - acc: 0.8696
Epoch 189/400
- 0s - loss: 1.0394 - acc: 0.9565
Epoch 190/400
- 0s - loss: 1.0272 - acc: 0.9130
Epoch 191/400
- 0s - loss: 1.0385 - acc: 0.9130
Epoch 192/400
- 0s - loss: 1.0257 - acc: 0.8696
Epoch 193/400
- 0s - loss: 1.0218 - acc: 0.8696
Epoch 194/400
- 0s - loss: 1.0193 - acc: 0.9565
Epoch 195/400
- 0s - loss: 1.0195 - acc: 0.9130
Epoch 196/400
- 0s - loss: 1.0137 - acc: 0.9130
Epoch 197/400
- 0s - loss: 1.0050 - acc: 0.8696
Epoch 198/400
- 0s - loss: 0.9985 - acc: 0.9130
Epoch 199/400
- 0s - loss: 1.0016 - acc: 0.9565
Epoch 200/400
- 0s - loss: 0.9917 - acc: 0.8696
Epoch 201/400
- 0s - loss: 0.9952 - acc: 0.9130
Epoch 202/400
- 0s - loss: 0.9823 - acc: 0.9130
Epoch 203/400
- 0s - loss: 0.9765 - acc: 0.9565
Epoch 204/400
- 0s - loss: 0.9722 - acc: 0.9565
Epoch 205/400
- 0s - loss: 0.9756 - acc: 0.9130
Epoch 206/400
- 0s - loss: 0.9733 - acc: 0.9130
Epoch 207/400
- 0s - loss: 0.9768 - acc: 0.8261
Epoch 208/400
- 0s - loss: 0.9611 - acc: 0.9565
Epoch 209/400
- 0s - loss: 0.9548 - acc: 0.9565
Epoch 210/400
- 0s - loss: 0.9530 - acc: 0.8696
Epoch 211/400
- 0s - loss: 0.9481 - acc: 0.8696
Epoch 212/400
- 0s - loss: 0.9436 - acc: 0.9130
Epoch 213/400
- 0s - loss: 0.9435 - acc: 0.8696
Epoch 214/400
- 0s - loss: 0.9430 - acc: 0.9130
Epoch 215/400
- 0s - loss: 0.9281 - acc: 0.9130
Epoch 216/400
- 0s - loss: 0.9267 - acc: 0.9565
Epoch 217/400
- 0s - loss: 0.9263 - acc: 0.9130
Epoch 218/400
- 0s - loss: 0.9180 - acc: 0.9565
Epoch 219/400
- 0s - loss: 0.9151 - acc: 0.9565
Epoch 220/400
- 0s - loss: 0.9125 - acc: 0.9130
Epoch 221/400
- 0s - loss: 0.9090 - acc: 0.8696
Epoch 222/400
- 0s - loss: 0.9039 - acc: 0.9565
Epoch 223/400
- 0s - loss: 0.9032 - acc: 0.9565
Epoch 224/400
- 0s - loss: 0.8966 - acc: 0.9130
Epoch 225/400
- 0s - loss: 0.8935 - acc: 0.9130
Epoch 226/400
- 0s - loss: 0.8946 - acc: 0.9130
Epoch 227/400
- 0s - loss: 0.8875 - acc: 0.9130
Epoch 228/400
- 0s - loss: 0.8872 - acc: 0.9565
Epoch 229/400
- 0s - loss: 0.8758 - acc: 0.9130
Epoch 230/400
- 0s - loss: 0.8746 - acc: 0.9565
Epoch 231/400
- 0s - loss: 0.8720 - acc: 0.9565
Epoch 232/400
- 0s - loss: 0.8724 - acc: 0.9130
Epoch 233/400
- 0s - loss: 0.8626 - acc: 0.9130
Epoch 234/400
- 0s - loss: 0.8615 - acc: 0.9130
Epoch 235/400
- 0s - loss: 0.8623 - acc: 0.9130
Epoch 236/400
- 0s - loss: 0.8575 - acc: 0.9565
Epoch 237/400
- 0s - loss: 0.8543 - acc: 0.9565
Epoch 238/400
- 0s - loss: 0.8498 - acc: 0.9565
Epoch 239/400
- 0s - loss: 0.8391 - acc: 0.9565
Epoch 240/400
- 0s - loss: 0.8426 - acc: 0.9130
Epoch 241/400
- 0s - loss: 0.8361 - acc: 0.8696
Epoch 242/400
- 0s - loss: 0.8354 - acc: 0.9130
Epoch 243/400
- 0s - loss: 0.8280 - acc: 0.9565
Epoch 244/400
- 0s - loss: 0.8233 - acc: 0.9130
Epoch 245/400
- 0s - loss: 0.8176 - acc: 0.9130
Epoch 246/400
- 0s - loss: 0.8149 - acc: 0.9565
Epoch 247/400
- 0s - loss: 0.8064 - acc: 0.9565
Epoch 248/400
- 0s - loss: 0.8156 - acc: 0.9565
Epoch 249/400
- 0s - loss: 0.8049 - acc: 0.9565
Epoch 250/400
- 0s - loss: 0.8014 - acc: 0.9565
Epoch 251/400
- 0s - loss: 0.7945 - acc: 0.9565
Epoch 252/400
- 0s - loss: 0.7918 - acc: 0.9565
Epoch 253/400
- 0s - loss: 0.7897 - acc: 0.9565
Epoch 254/400
- 0s - loss: 0.7859 - acc: 0.9565
Epoch 255/400
- 0s - loss: 0.7810 - acc: 0.9565
Epoch 256/400
- 0s - loss: 0.7760 - acc: 0.9565
Epoch 257/400
- 0s - loss: 0.7822 - acc: 0.9130
Epoch 258/400
- 0s - loss: 0.7783 - acc: 0.9565
Epoch 259/400
- 0s - loss: 0.7672 - acc: 0.9565
Epoch 260/400
- 0s - loss: 0.7705 - acc: 0.9565
Epoch 261/400
- 0s - loss: 0.7659 - acc: 0.9565
Epoch 262/400
- 0s - loss: 0.7604 - acc: 0.9565
Epoch 263/400
- 0s - loss: 0.7585 - acc: 0.9565
Epoch 264/400
- 0s - loss: 0.7564 - acc: 0.9565
Epoch 265/400
- 0s - loss: 0.7527 - acc: 0.9565
Epoch 266/400
- 0s - loss: 0.7418 - acc: 0.9565
Epoch 267/400
- 0s - loss: 0.7425 - acc: 0.9565
Epoch 268/400
- 0s - loss: 0.7351 - acc: 0.9565
Epoch 269/400
- 0s - loss: 0.7425 - acc: 0.9565
Epoch 270/400
- 0s - loss: 0.7334 - acc: 0.9565
Epoch 271/400
- 0s - loss: 0.7315 - acc: 0.9565
Epoch 272/400
- 0s - loss: 0.7305 - acc: 0.9565
Epoch 273/400
- 0s - loss: 0.7183 - acc: 0.9565
Epoch 274/400
- 0s - loss: 0.7198 - acc: 0.9565
Epoch 275/400
- 0s - loss: 0.7197 - acc: 1.0000
Epoch 276/400
- 0s - loss: 0.7125 - acc: 0.9565
Epoch 277/400
- 0s - loss: 0.7105 - acc: 1.0000
Epoch 278/400
- 0s - loss: 0.7074 - acc: 0.9565
Epoch 279/400
- 0s - loss: 0.7033 - acc: 0.9565
Epoch 280/400
- 0s - loss: 0.6993 - acc: 0.9565
Epoch 281/400
- 0s - loss: 0.6954 - acc: 0.9565
Epoch 282/400
- 0s - loss: 0.6952 - acc: 0.9565
Epoch 283/400
- 0s - loss: 0.6964 - acc: 0.9565
Epoch 284/400
- 0s - loss: 0.6862 - acc: 0.9565
Epoch 285/400
- 0s - loss: 0.6928 - acc: 0.9565
Epoch 286/400
- 0s - loss: 0.6861 - acc: 0.9565
Epoch 287/400
- 0s - loss: 0.6760 - acc: 0.9565
Epoch 288/400
- 0s - loss: 0.6756 - acc: 0.9565
Epoch 289/400
- 0s - loss: 0.6821 - acc: 0.9565
Epoch 290/400
- 0s - loss: 0.6716 - acc: 0.9565
Epoch 291/400
- 0s - loss: 0.6671 - acc: 0.9565
Epoch 292/400
- 0s - loss: 0.6652 - acc: 0.9565
Epoch 293/400
- 0s - loss: 0.6594 - acc: 1.0000
Epoch 294/400
- 0s - loss: 0.6568 - acc: 1.0000
Epoch 295/400
- 0s - loss: 0.6503 - acc: 1.0000
Epoch 296/400
- 0s - loss: 0.6498 - acc: 1.0000
Epoch 297/400
- 0s - loss: 0.6441 - acc: 0.9565
Epoch 298/400
- 0s - loss: 0.6420 - acc: 0.9565
Epoch 299/400
- 0s - loss: 0.6418 - acc: 0.9565
Epoch 300/400
- 0s - loss: 0.6375 - acc: 0.9565
Epoch 301/400
- 0s - loss: 0.6368 - acc: 0.9565
Epoch 302/400
- 0s - loss: 0.6328 - acc: 0.9565
Epoch 303/400
- 0s - loss: 0.6341 - acc: 0.9565
Epoch 304/400
- 0s - loss: 0.6246 - acc: 0.9565
Epoch 305/400
- 0s - loss: 0.6265 - acc: 0.9565
Epoch 306/400
- 0s - loss: 0.6285 - acc: 0.9565
Epoch 307/400
- 0s - loss: 0.6145 - acc: 0.9565
Epoch 308/400
- 0s - loss: 0.6174 - acc: 0.9565
Epoch 309/400
- 0s - loss: 0.6137 - acc: 0.9565
Epoch 310/400
- 0s - loss: 0.6069 - acc: 0.9565
Epoch 311/400
- 0s - loss: 0.6028 - acc: 0.9565
Epoch 312/400
- 0s - loss: 0.6075 - acc: 0.9565
Epoch 313/400
- 0s - loss: 0.6018 - acc: 0.9565
Epoch 314/400
- 0s - loss: 0.5959 - acc: 1.0000
Epoch 315/400
- 0s - loss: 0.6004 - acc: 1.0000
Epoch 316/400
- 0s - loss: 0.6125 - acc: 0.9565
Epoch 317/400
- 0s - loss: 0.5984 - acc: 0.9565
Epoch 318/400
- 0s - loss: 0.5873 - acc: 1.0000
Epoch 319/400
- 0s - loss: 0.5860 - acc: 0.9565
Epoch 320/400
- 0s - loss: 0.5847 - acc: 1.0000
Epoch 321/400
- 0s - loss: 0.5752 - acc: 1.0000
Epoch 322/400
- 0s - loss: 0.5766 - acc: 0.9565
Epoch 323/400
- 0s - loss: 0.5750 - acc: 0.9565
Epoch 324/400
- 0s - loss: 0.5716 - acc: 0.9565
Epoch 325/400
- 0s - loss: 0.5647 - acc: 0.9565
Epoch 326/400
- 0s - loss: 0.5655 - acc: 1.0000
Epoch 327/400
- 0s - loss: 0.5665 - acc: 0.9565
Epoch 328/400
- 0s - loss: 0.5564 - acc: 0.9565
Epoch 329/400
- 0s - loss: 0.5576 - acc: 0.9565
Epoch 330/400
- 0s - loss: 0.5532 - acc: 0.9565
Epoch 331/400
- 0s - loss: 0.5512 - acc: 1.0000
Epoch 332/400
- 0s - loss: 0.5471 - acc: 1.0000
Epoch 333/400
- 0s - loss: 0.5410 - acc: 0.9565
Epoch 334/400
- 0s - loss: 0.5383 - acc: 0.9565
Epoch 335/400
- 0s - loss: 0.5384 - acc: 0.9565
Epoch 336/400
- 0s - loss: 0.5364 - acc: 1.0000
Epoch 337/400
- 0s - loss: 0.5335 - acc: 1.0000
Epoch 338/400
- 0s - loss: 0.5356 - acc: 1.0000
Epoch 339/400
- 0s - loss: 0.5265 - acc: 0.9565
Epoch 340/400
- 0s - loss: 0.5293 - acc: 1.0000
Epoch 341/400
- 0s - loss: 0.5185 - acc: 1.0000
Epoch 342/400
- 0s - loss: 0.5173 - acc: 1.0000
Epoch 343/400
- 0s - loss: 0.5162 - acc: 0.9565
Epoch 344/400
- 0s - loss: 0.5161 - acc: 0.9565
Epoch 345/400
- 0s - loss: 0.5190 - acc: 0.9565
Epoch 346/400
- 0s - loss: 0.5180 - acc: 1.0000
Epoch 347/400
- 0s - loss: 0.5265 - acc: 0.9565
Epoch 348/400
- 0s - loss: 0.5096 - acc: 1.0000
Epoch 349/400
- 0s - loss: 0.5038 - acc: 1.0000
Epoch 350/400
- 0s - loss: 0.4985 - acc: 0.9565
Epoch 351/400
- 0s - loss: 0.5008 - acc: 1.0000
Epoch 352/400
- 0s - loss: 0.4996 - acc: 1.0000
Epoch 353/400
- 0s - loss: 0.4922 - acc: 1.0000
Epoch 354/400
- 0s - loss: 0.4895 - acc: 0.9565
Epoch 355/400
- 0s - loss: 0.4833 - acc: 0.9565
Epoch 356/400
- 0s - loss: 0.4889 - acc: 1.0000
Epoch 357/400
- 0s - loss: 0.4822 - acc: 0.9565
Epoch 358/400
- 0s - loss: 0.4850 - acc: 0.9565
Epoch 359/400
- 0s - loss: 0.4770 - acc: 1.0000
Epoch 360/400
- 0s - loss: 0.4741 - acc: 1.0000
Epoch 361/400
- 0s - loss: 0.4734 - acc: 0.9565
Epoch 362/400
- 0s - loss: 0.4705 - acc: 0.9565
Epoch 363/400
- 0s - loss: 0.4677 - acc: 0.9565
Epoch 364/400
- 0s - loss: 0.4648 - acc: 1.0000
Epoch 365/400
- 0s - loss: 0.4643 - acc: 1.0000
Epoch 366/400
- 0s - loss: 0.4612 - acc: 0.9565
Epoch 367/400
- 0s - loss: 0.4572 - acc: 1.0000
Epoch 368/400
- 0s - loss: 0.4559 - acc: 1.0000
Epoch 369/400
- 0s - loss: 0.4512 - acc: 1.0000
Epoch 370/400
- 0s - loss: 0.4534 - acc: 1.0000
Epoch 371/400
- 0s - loss: 0.4496 - acc: 1.0000
Epoch 372/400
- 0s - loss: 0.4516 - acc: 0.9565
Epoch 373/400
- 0s - loss: 0.4449 - acc: 1.0000
Epoch 374/400
- 0s - loss: 0.4391 - acc: 1.0000
Epoch 375/400
- 0s - loss: 0.4428 - acc: 0.9565
Epoch 376/400
- 0s - loss: 0.4387 - acc: 0.9565
Epoch 377/400
- 0s - loss: 0.4451 - acc: 1.0000
Epoch 378/400
- 0s - loss: 0.4336 - acc: 1.0000
Epoch 379/400
- 0s - loss: 0.4297 - acc: 1.0000
Epoch 380/400
- 0s - loss: 0.4264 - acc: 0.9565
Epoch 381/400
- 0s - loss: 0.4266 - acc: 1.0000
Epoch 382/400
- 0s - loss: 0.4333 - acc: 0.9565
Epoch 383/400
- 0s - loss: 0.4325 - acc: 1.0000
Epoch 384/400
- 0s - loss: 0.4246 - acc: 1.0000
Epoch 385/400
- 0s - loss: 0.4169 - acc: 1.0000
Epoch 386/400
- 0s - loss: 0.4133 - acc: 1.0000
Epoch 387/400
- 0s - loss: 0.4156 - acc: 1.0000
Epoch 388/400
- 0s - loss: 0.4162 - acc: 1.0000
Epoch 389/400
- 0s - loss: 0.4086 - acc: 1.0000
Epoch 390/400
- 0s - loss: 0.4061 - acc: 1.0000
Epoch 391/400
- 0s - loss: 0.4045 - acc: 1.0000
Epoch 392/400
- 0s - loss: 0.4058 - acc: 0.9565
Epoch 393/400
- 0s - loss: 0.3974 - acc: 1.0000
Epoch 394/400
- 0s - loss: 0.3964 - acc: 1.0000
Epoch 395/400
- 0s - loss: 0.3930 - acc: 1.0000
Epoch 396/400
- 0s - loss: 0.3981 - acc: 1.0000
Epoch 397/400
- 0s - loss: 0.3871 - acc: 1.0000
Epoch 398/400
- 0s - loss: 0.3853 - acc: 1.0000
Epoch 399/400
- 0s - loss: 0.3805 - acc: 1.0000
Epoch 400/400
- 0s - loss: 0.3810 - acc: 1.0000
23/23 [==============================] - 1s 33ms/step
Model Accuracy: 100.00%
['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> M
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> P
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> S
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> U
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> W
['U', 'V', 'W'] -> X
['V', 'W', 'X'] -> Y
['W', 'X', 'Y'] -> Z
(X.shape[1], X.shape[2]) # the input shape to LSTM layer with 32 neurons is given by dimensions of time-steps and features
X.shape[0], y.shape[1] # number of examples and number of categorical outputs
Memory and context
If this network is learning the way we would like, it should be robust to noise and also understand the relative context (in this case, where a prior letter occurs in the sequence).
I.e., we should be able to give it corrupted sequences, and it should produce reasonably correct predictions.
Make the following change to the code to test this out:
You Try!
- We'll use "W" for our erroneous/corrupted data element
- Add code at the end to predict on the following sequences:
- 'WBC', 'WKL', 'WTU', 'DWF', 'MWO', 'VWW', 'GHW', 'JKW', 'PQW'
- Notice any pattern? Hard to tell from a small sample, but if you play with it (trying sequences from different places in the alphabet, or different "corruption" letters, you'll notice patterns that give a hint at what the network is learning
The solution is in 060_DLByABr_05a-LSTM-Solution if you are lazy right now or get stuck.
Pretty cool... BUT
This alphabet example does seem a bit like "tennis without the net" since the original goal was to develop networks that could extract patterns from complex, ambiguous content like natural language or music, and we've been playing with a sequence (Roman alphabet) that is 100% deterministic and tiny in size.
First, go ahead and start 061_DLByABr_05b-LSTM-Language since it will take several minutes to produce its first output.
This latter script is taken 100% exactly as-is from the Keras library examples folder (https://github.com/fchollet/keras/blob/master/examples/lstmtextgeneration.py) and uses precisely the logic we just learned, in order to learn and synthesize English language text from a single-author corpuse. The amazing thing is that the text is learned and generated one letter at a time, just like we did with the alphabet.
Compared to our earlier examples... * there is a minor difference in the way the inputs are encoded, using 1-hot vectors * and there is a significant difference in the way the outputs (predictions) are generated: instead of taking just the most likely output class (character) via argmax as we did before, this time we are treating the output as a distribution and sampling from the distribution.
Let's take a look at the code ... but even so, this will probably be something to come back to after fika or a long break, as the training takes about 5 minutes per epoch (late 2013 MBP CPU) and we need around 20 epochs (80 minutes!) to get good output.
import sys
sys.exit(0) #just to keep from accidentally running this code (that is already in 061_DLByABr_05b-LSTM-Language) HERE
'''Example script to generate text from Nietzsche's writings.
At least 20 epochs are required before the generated text
starts sounding coherent.
It is recommended to run this script on GPU, as recurrent
networks are quite computationally intensive.
If you try this script on new data, make sure your corpus
has at least ~100k characters. ~1M is better.
'''
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LSTM
from keras.optimizers import RMSprop
from keras.utils.data_utils import get_file
import numpy as np
import random
import sys
path = "../data/nietzsche.txt"
text = open(path).read().lower()
print('corpus length:', len(text))
chars = sorted(list(set(text)))
print('total chars:', len(chars))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
# cut the text in semi-redundant sequences of maxlen characters
maxlen = 40
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
print('nb sequences:', len(sentences))
print('Vectorization...')
X = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
# build the model: a single LSTM
print('Build model...')
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(chars))))
model.add(Dense(len(chars)))
model.add(Activation('softmax'))
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
def sample(preds, temperature=1.0):
# helper function to sample an index from a probability array
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / temperature
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)
# train the model, output generated text after each iteration
for iteration in range(1, 60):
print()
print('-' * 50)
print('Iteration', iteration)
model.fit(X, y, batch_size=128, epochs=1)
start_index = random.randint(0, len(text) - maxlen - 1)
for diversity in [0.2, 0.5, 1.0, 1.2]:
print()
print('----- diversity:', diversity)
generated = ''
sentence = text[start_index: start_index + maxlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(400):
x = np.zeros((1, maxlen, len(chars)))
for t, char in enumerate(sentence):
x[0, t, char_indices[char]] = 1.
preds = model.predict(x, verbose=0)[0]
next_index = sample(preds, diversity)
next_char = indices_char[next_index]
generated += next_char
sentence = sentence[1:] + next_char
sys.stdout.write(next_char)
sys.stdout.flush()
print()
/databricks/python/lib/python3.7/site-packages/IPython/core/interactiveshell.py:3304: UserWarning: To exit: use 'exit', 'quit', or Ctrl-D.
warn("To exit: use 'exit', 'quit', or Ctrl-D.", stacklevel=1)
Gated Recurrent Unit (GRU)
In 2014, a new, promising design for RNN units called Gated Recurrent Unit was published (https://arxiv.org/abs/1412.3555)
GRUs have performed similarly to LSTMs, but are slightly simpler in design:
- GRU has just two gates: "update" and "reset" (instead of the input, output, and forget in LSTM)
- update controls how to modify (weight and keep) cell state
- reset controls how new input is mixed (weighted) with/against memorized state
- there is no output gate, so the cell state is propagated out -- i.e., there is no "hidden" state that is separate from the generated output state

Which one should you use for which applications? The jury is still out -- this is an area for experimentation!
Using GRUs in Keras
... is as simple as using the built-in GRU class (https://keras.io/layers/recurrent/)
If you are working with RNNs, spend some time with docs to go deeper, as we have just barely scratched the surface here, and there are many "knobs" to turn that will help things go right (or wrong).
'''Example script to generate text from Nietzsche's writings.
At least 20 epochs are required before the generated text
starts sounding coherent.
It is recommended to run this script on GPU, as recurrent
networks are quite computationally intensive.
If you try this script on new data, make sure your corpus
has at least ~100k characters. ~1M is better.
'''
from __future__ import print_function
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LSTM
from keras.optimizers import RMSprop
from keras.utils.data_utils import get_file
import numpy as np
import random
import sys
path = get_file('nietzsche.txt', origin='https://s3.amazonaws.com/text-datasets/nietzsche.txt')
text = open(path).read().lower()
print('corpus length:', len(text))
chars = sorted(list(set(text)))
print('total chars:', len(chars))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
# cut the text in semi-redundant sequences of maxlen characters
maxlen = 40
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
print('nb sequences:', len(sentences))
print('Vectorization...')
X = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
corpus length: 600893
total chars: 57
nb sequences: 200285
Vectorization...
ls
conf
derby.log
eventlogs
ganglia
logs
len(sentences), maxlen, len(chars)
X
What Does Our Nietzsche Generator Produce?
Here are snapshots from middle and late in a training run.
Iteration 19
Iteration 19
Epoch 1/1
200287/200287 [==============================] - 262s - loss: 1.3908
----- diversity: 0.2
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions of the present of the supersially and the soul. the spirituality of the same of the soul. the protect and in the states to the supersially and the soul, in the supersially the supersially and the concerning and in the most conscience of the soul. the soul. the concerning and the substances, and the philosophers in the sing"--that is the most supersiall and the philosophers of the supersially of t
----- diversity: 0.5
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions are more there is the scientific modern to the head in the concerning in the same old will of the excited of science. many all the possible concerning such laugher according to when the philosophers sense of men of univerself, the most lacked same depresse in the point, which is desires of a "good (who has senses on that one experiencess which use the concerning and in the respect of the same ori
----- diversity: 1.0
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions expressions--are interest person from indeed to ordinapoon as or one of
the uphamy, state is rivel stimromannes are lot man of soul"--modile what he woulds hope in a riligiation, is conscience, and you amy, surposit to advanced torturily
and whorlon and perressing for accurcted with a lot us in view, of its own vanity of their natest"--learns, and dis predeceared from and leade, for oted those wi
----- diversity: 1.2
----- Generating with seed: " apart from the value of such assertions"
apart from the value of such assertions of
rutould chinates
rested exceteds to more saarkgs testure carevan, accordy owing before fatherly rifiny,
thrurgins of novelts "frous inventive earth as dire!ition he
shate out of itst sacrifice, in this
mectalical
inworle, you
adome enqueres to its ighter. he often. once even with ded threaten"! an eebirelesifist.
lran innoting
with we canone acquire at them crarulents who had prote will out t
Iteration 32
Iteration 32
Epoch 1/1
200287/200287 [==============================] - 255s - loss: 1.3830
----- diversity: 0.2
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, and in the great present of the sort of the strangern that is and in the sologies and the experiences and the present of the present and science of the probably a subject of the subject of the morality and morality of the soul the experiences the morality of the experiences of the conscience in the soul and more the experiences the strangere and present the rest the strangere and individual of th
----- diversity: 0.5
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, and in the morality of which we knows upon the english and insigning things be exception of
consequences of the man and explained its more in the senses for the same ordinary and the sortarians and subjects and simily in a some longing the destiny ordinary. man easily that has been the some subject and say, and and and and does not to power as all the reasonable and distinction of this one betray
----- diversity: 1.0
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, surrespossifilice view and life fundamental worthing more sirer. holestly
and whan to be
dream. in whom hand that one downgk edplenius will almost eyes brocky that we wills stupid dor
oborbbill to be dimorable
great excet of ifysabless. the good take the historical yet right by guntend, and which fuens the irrelias in literals in finally to the same flild, conditioned when where prom. it has behi
----- diversity: 1.2
----- Generating with seed: " body, as a part of this external
world,"
body, as a part of this external
world, easily achosed time mantur makeches on this
vanity, obcame-scompleises. but inquire-calr ever powerfully smorais: too-wantse; when thoue
conducting
unconstularly without least gainstyfyerfulled to wo
has upos
among uaxqunct what is mell "loves and
lamacity what mattery of upon the a. and which oasis seour schol
to power: the passion sparabrated will. in his europers raris! what seems to these her
Iteration 38
Iteration 38
Epoch 1/1
200287/200287 [==============================] - 256s - loss: 7.6662
----- diversity: 0.2
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughteesen a a a= at ae i is es4 iei aatee he a a ac oyte in ioie aan a atoe aie ion a atias a ooe o e tin exanat moe ao is aon e a ntiere t i in ate an on a e as the a ion aisn ost aed i i ioiesn les?ane i ee to i o ate o igice thi io an a xen an ae an teane one ee e alouieis asno oie on i a a ae s as n io a an e a ofe e oe ehe it aiol s a aeio st ior ooe an io e ot io o i aa9em aan ev a
----- diversity: 0.5
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughteese a on eionea] aooooi ate uo e9l hoe atae s in eaae an on io]e nd ast aais ta e od iia ng ac ee er ber in ==st a se is ao o e as aeian iesee tee otiane o oeean a ieatqe o asnone anc
oo a t
tee sefiois to an at in ol asnse an o e e oo ie oae asne at a ait iati oese se a e p ie peen iei ien o oot inees engied evone t oen oou atipeem a sthen ion assise ti a a s itos io ae an eees as oi
----- diversity: 1.0
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughteena te e ore te beosespeehsha ieno atit e ewge ou ino oo oee coatian aon ie ac aalle e a o die eionae oa att uec a acae ao a an eess as
o i a io a oe a e is as oo in ene xof o oooreeg ta m eon al iii n p daesaoe n ite o ane tio oe anoo t ane
s i e tioo ise s a asi e ana ooe ote soueeon io on atieaneyc ei it he se it is ao e an ime ane on eronaa ee itouman io e ato an ale a mae taoa ien
----- diversity: 1.2
----- Generating with seed: "erable? for there is no
longer any ought"
erable? for there is no
longer any oughti o aa e2senoees yi i e datssateal toeieie e a o zanato aal arn aseatli oeene aoni le eoeod t aes a isoee tap e o . is oi astee an ea titoe e a exeeee thui itoan ain eas a e bu inen ao ofa ie e e7n anae ait ie a ve er inen ite
as oe of heangi eestioe orasb e fie o o o a eean o ot odeerean io io oae ooe ne " e istee esoonae e terasfioees asa ehainoet at e ea ai esoon ano a p eesas e aitie
(raaz)
'Mind the Hype' around AI
Pay attention to biases in various media.
- Guardian: 'He began to eat Hermione's family': bot tries to write Harry Potter book – and fails in magic ways After being fed all seven Potter tales, a predictive keyboard has produced a tale that veers from almost genuine to gloriously bonkers
- Business Insider: There is a new chapter in Harry Potter's story — and it was written by artificial intelligence ... The writing is mostly weird and borderline comical, but the machine managed to partly reproduce original writer J.K. Rowling's writing style.
When your managers get "psyched" about how AI will solve all the problems and your sales teams are dreaming hard - keep it cool and manage their expectations as a practical data scientist who is humbled by the hard reality of additions, multiplications and conditionals under the hood.
'Mind the Ethics'
Don't forget to ask how your data science pipelines could adversely affect peoples: * A great X-mas gift to yourself: https://weaponsofmathdestructionbook.com/ * Another one to make you braver and calmer: https://www.schneier.com/books/dataandgoliath/
Don't forget that Data Scientists can be put behind bars for "following orders" from your boss to "make magic happen". * https://www.datasciencecentral.com/profiles/blogs/doing-illegal-data-science-without-knowing-it * https://timesofindia.indiatimes.com/india/forecast-of-poll-results-illegal-election-commission/articleshow/57927839.cms * https://spectrum.ieee.org/cars-that-think/at-work/education/vw-scandal-shocking-but-not-surprising-ethicists-say * ...
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.utils import np_utils
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print (seq_in, '->', seq_out)
# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))
X = X / float(len(alphabet))
y = np_utils.to_categorical(dataY)
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=400, batch_size=1, verbose=2)
scores = model.evaluate(X, y)
print("Model Accuracy: %.2f%%" % (scores[1]*100))
for pattern in ['WBC', 'WKL', 'WTU', 'DWF', 'MWO', 'VWW', 'GHW', 'JKW', 'PQW']:
pattern = [char_to_int[c] for c in pattern]
x = numpy.reshape(pattern, (1, len(pattern), 1))
x = x / float(len(alphabet))
prediction = model.predict(x, verbose=0)
index = numpy.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
print (seq_in, "->", result)
Using TensorFlow backend.
ABC -> D
BCD -> E
CDE -> F
DEF -> G
EFG -> H
FGH -> I
GHI -> J
HIJ -> K
IJK -> L
JKL -> M
KLM -> N
LMN -> O
MNO -> P
NOP -> Q
OPQ -> R
PQR -> S
QRS -> T
RST -> U
STU -> V
TUV -> W
UVW -> X
VWX -> Y
WXY -> Z
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Epoch 1/400
- 1s - loss: 3.2607 - acc: 0.0435
Epoch 2/400
- 0s - loss: 3.2471 - acc: 0.0435
Epoch 3/400
- 0s - loss: 3.2406 - acc: 0.0435
Epoch 4/400
- 0s - loss: 3.2340 - acc: 0.0435
Epoch 5/400
- 0s - loss: 3.2268 - acc: 0.0435
Epoch 6/400
- 0s - loss: 3.2188 - acc: 0.0435
Epoch 7/400
- 0s - loss: 3.2119 - acc: 0.0000e+00
Epoch 8/400
- 0s - loss: 3.2032 - acc: 0.0000e+00
Epoch 9/400
- 0s - loss: 3.1923 - acc: 0.0000e+00
Epoch 10/400
- 0s - loss: 3.1813 - acc: 0.0000e+00
Epoch 11/400
- 0s - loss: 3.1704 - acc: 0.0000e+00
Epoch 12/400
- 0s - loss: 3.1563 - acc: 0.0000e+00
Epoch 13/400
- 0s - loss: 3.1418 - acc: 0.0435
Epoch 14/400
- 0s - loss: 3.1271 - acc: 0.0000e+00
Epoch 15/400
- 0s - loss: 3.1095 - acc: 0.0435
Epoch 16/400
- 0s - loss: 3.0919 - acc: 0.0435
Epoch 17/400
- 0s - loss: 3.0732 - acc: 0.0435
Epoch 18/400
- 0s - loss: 3.0534 - acc: 0.0435
Epoch 19/400
- 0s - loss: 3.0314 - acc: 0.0435
Epoch 20/400
- 0s - loss: 3.0114 - acc: 0.0000e+00
Epoch 21/400
- 0s - loss: 2.9832 - acc: 0.0000e+00
Epoch 22/400
- 0s - loss: 2.9516 - acc: 0.0435
Epoch 23/400
- 0s - loss: 2.9206 - acc: 0.0870
Epoch 24/400
- 0s - loss: 2.8855 - acc: 0.1304
Epoch 25/400
- 0s - loss: 2.8390 - acc: 0.0435
Epoch 26/400
- 0s - loss: 2.7914 - acc: 0.0435
Epoch 27/400
- 0s - loss: 2.7509 - acc: 0.0435
Epoch 28/400
- 0s - loss: 2.6969 - acc: 0.0870
Epoch 29/400
- 0s - loss: 2.6545 - acc: 0.0435
Epoch 30/400
- 0s - loss: 2.6108 - acc: 0.0870
Epoch 31/400
- 0s - loss: 2.5731 - acc: 0.0435
Epoch 32/400
- 0s - loss: 2.5345 - acc: 0.0870
Epoch 33/400
- 0s - loss: 2.5017 - acc: 0.0435
Epoch 34/400
- 0s - loss: 2.4686 - acc: 0.1304
Epoch 35/400
- 0s - loss: 2.4437 - acc: 0.0870
Epoch 36/400
- 0s - loss: 2.4134 - acc: 0.1304
Epoch 37/400
- 0s - loss: 2.3951 - acc: 0.1304
Epoch 38/400
- 0s - loss: 2.3646 - acc: 0.1304
Epoch 39/400
- 0s - loss: 2.3386 - acc: 0.1304
Epoch 40/400
- 0s - loss: 2.3184 - acc: 0.1739
Epoch 41/400
- 0s - loss: 2.2917 - acc: 0.1304
Epoch 42/400
- 0s - loss: 2.2671 - acc: 0.1304
Epoch 43/400
- 0s - loss: 2.2335 - acc: 0.2174
Epoch 44/400
- 0s - loss: 2.2171 - acc: 0.1739
Epoch 45/400
- 0s - loss: 2.1917 - acc: 0.1739
Epoch 46/400
- 0s - loss: 2.1575 - acc: 0.1739
Epoch 47/400
- 0s - loss: 2.1401 - acc: 0.1739
Epoch 48/400
- 0s - loss: 2.1176 - acc: 0.0870
Epoch 49/400
- 0s - loss: 2.0948 - acc: 0.2174
Epoch 50/400
- 0s - loss: 2.0782 - acc: 0.2174
Epoch 51/400
- 0s - loss: 2.0612 - acc: 0.2174
Epoch 52/400
- 0s - loss: 2.0398 - acc: 0.3043
Epoch 53/400
- 0s - loss: 2.0150 - acc: 0.2174
Epoch 54/400
- 0s - loss: 1.9948 - acc: 0.2609
Epoch 55/400
- 0s - loss: 1.9834 - acc: 0.2609
Epoch 56/400
- 0s - loss: 1.9608 - acc: 0.3478
Epoch 57/400
- 0s - loss: 1.9438 - acc: 0.2609
Epoch 58/400
- 0s - loss: 1.9316 - acc: 0.3913
Epoch 59/400
- 0s - loss: 1.9126 - acc: 0.2609
Epoch 60/400
- 0s - loss: 1.9025 - acc: 0.3043
Epoch 61/400
- 0s - loss: 1.8868 - acc: 0.2609
Epoch 62/400
- 0s - loss: 1.8789 - acc: 0.2174
Epoch 63/400
- 0s - loss: 1.8545 - acc: 0.2174
Epoch 64/400
- 0s - loss: 1.8475 - acc: 0.3043
Epoch 65/400
- 0s - loss: 1.8338 - acc: 0.2609
Epoch 66/400
- 0s - loss: 1.8265 - acc: 0.3478
Epoch 67/400
- 0s - loss: 1.8118 - acc: 0.3043
Epoch 68/400
- 0s - loss: 1.7896 - acc: 0.3478
Epoch 69/400
- 0s - loss: 1.7823 - acc: 0.3043
Epoch 70/400
- 0s - loss: 1.7655 - acc: 0.4783
Epoch 71/400
- 0s - loss: 1.7583 - acc: 0.4348
Epoch 72/400
- 0s - loss: 1.7516 - acc: 0.3478
Epoch 73/400
- 0s - loss: 1.7415 - acc: 0.3043
Epoch 74/400
- 0s - loss: 1.7327 - acc: 0.4348
Epoch 75/400
- 0s - loss: 1.7153 - acc: 0.3913
Epoch 76/400
- 0s - loss: 1.7080 - acc: 0.3478
Epoch 77/400
- 0s - loss: 1.6930 - acc: 0.3478
Epoch 78/400
- 0s - loss: 1.6934 - acc: 0.4348
Epoch 79/400
- 0s - loss: 1.6783 - acc: 0.4348
Epoch 80/400
- 0s - loss: 1.6727 - acc: 0.4783
Epoch 81/400
- 0s - loss: 1.6616 - acc: 0.4348
Epoch 82/400
- 0s - loss: 1.6524 - acc: 0.4348
Epoch 83/400
- 0s - loss: 1.6392 - acc: 0.5652
Epoch 84/400
- 0s - loss: 1.6321 - acc: 0.6522
Epoch 85/400
- 0s - loss: 1.6241 - acc: 0.5217
Epoch 86/400
- 0s - loss: 1.6140 - acc: 0.6522
Epoch 87/400
- 0s - loss: 1.6054 - acc: 0.5652
Epoch 88/400
- 0s - loss: 1.5969 - acc: 0.6087
Epoch 89/400
- 0s - loss: 1.5884 - acc: 0.5652
Epoch 90/400
- 0s - loss: 1.5831 - acc: 0.5217
Epoch 91/400
- 0s - loss: 1.5750 - acc: 0.5652
Epoch 92/400
- 0s - loss: 1.5625 - acc: 0.6522
Epoch 93/400
- 0s - loss: 1.5559 - acc: 0.6957
Epoch 94/400
- 0s - loss: 1.5512 - acc: 0.6957
Epoch 95/400
- 0s - loss: 1.5378 - acc: 0.6957
Epoch 96/400
- 0s - loss: 1.5266 - acc: 0.7391
Epoch 97/400
- 0s - loss: 1.5172 - acc: 0.6522
Epoch 98/400
- 0s - loss: 1.5146 - acc: 0.6522
Epoch 99/400
- 0s - loss: 1.5055 - acc: 0.6522
Epoch 100/400
- 0s - loss: 1.4920 - acc: 0.6957
Epoch 101/400
- 0s - loss: 1.4909 - acc: 0.7826
Epoch 102/400
- 0s - loss: 1.4820 - acc: 0.6957
Epoch 103/400
- 0s - loss: 1.4706 - acc: 0.6957
Epoch 104/400
- 0s - loss: 1.4739 - acc: 0.7391
Epoch 105/400
- 0s - loss: 1.4650 - acc: 0.6957
Epoch 106/400
- 0s - loss: 1.4545 - acc: 0.7391
Epoch 107/400
- 0s - loss: 1.4526 - acc: 0.7391
Epoch 108/400
- 0s - loss: 1.4383 - acc: 0.7391
Epoch 109/400
- 0s - loss: 1.4341 - acc: 0.6957
Epoch 110/400
- 0s - loss: 1.4214 - acc: 0.6957
Epoch 111/400
- 0s - loss: 1.4173 - acc: 0.7826
Epoch 112/400
- 0s - loss: 1.4146 - acc: 0.7391
Epoch 113/400
- 0s - loss: 1.4028 - acc: 0.6957
Epoch 114/400
- 0s - loss: 1.3965 - acc: 0.7391
Epoch 115/400
- 0s - loss: 1.3840 - acc: 0.6957
Epoch 116/400
- 0s - loss: 1.3815 - acc: 0.6957
Epoch 117/400
- 0s - loss: 1.3780 - acc: 0.6957
Epoch 118/400
- 0s - loss: 1.3642 - acc: 0.7826
Epoch 119/400
- 0s - loss: 1.3611 - acc: 0.6957
Epoch 120/400
- 0s - loss: 1.3554 - acc: 0.8261
Epoch 121/400
- 0s - loss: 1.3459 - acc: 0.7826
Epoch 122/400
- 0s - loss: 1.3397 - acc: 0.6957
Epoch 123/400
- 0s - loss: 1.3315 - acc: 0.7391
Epoch 124/400
- 0s - loss: 1.3299 - acc: 0.7391
Epoch 125/400
- 0s - loss: 1.3273 - acc: 0.6957
Epoch 126/400
- 0s - loss: 1.3126 - acc: 0.7391
Epoch 127/400
- 0s - loss: 1.3127 - acc: 0.8261
Epoch 128/400
- 0s - loss: 1.3052 - acc: 0.7826
Epoch 129/400
- 0s - loss: 1.3013 - acc: 0.7826
Epoch 130/400
- 0s - loss: 1.2956 - acc: 0.8261
Epoch 131/400
- 0s - loss: 1.2823 - acc: 0.8261
Epoch 132/400
- 0s - loss: 1.2840 - acc: 0.7826
Epoch 133/400
- 0s - loss: 1.2661 - acc: 0.7826
Epoch 134/400
- 0s - loss: 1.2652 - acc: 0.7826
Epoch 135/400
- 0s - loss: 1.2592 - acc: 0.8696
Epoch 136/400
- 0s - loss: 1.2529 - acc: 0.8261
Epoch 137/400
- 0s - loss: 1.2499 - acc: 0.8261
Epoch 138/400
- 0s - loss: 1.2379 - acc: 0.8261
Epoch 139/400
- 0s - loss: 1.2483 - acc: 0.8261
Epoch 140/400
- 0s - loss: 1.2352 - acc: 0.8261
Epoch 141/400
- 0s - loss: 1.2215 - acc: 0.8261
Epoch 142/400
- 0s - loss: 1.2234 - acc: 0.7826
Epoch 143/400
- 0s - loss: 1.2134 - acc: 0.8261
Epoch 144/400
- 0s - loss: 1.2076 - acc: 0.8261
Epoch 145/400
- 0s - loss: 1.2023 - acc: 0.8261
Epoch 146/400
- 0s - loss: 1.1932 - acc: 0.8261
Epoch 147/400
- 0s - loss: 1.1943 - acc: 0.8696
Epoch 148/400
- 0s - loss: 1.1852 - acc: 0.8696
Epoch 149/400
- 0s - loss: 1.1806 - acc: 0.7826
Epoch 150/400
- 0s - loss: 1.1755 - acc: 0.8261
Epoch 151/400
- 0s - loss: 1.1730 - acc: 0.8696
Epoch 152/400
- 0s - loss: 1.1625 - acc: 0.8261
Epoch 153/400
- 0s - loss: 1.1569 - acc: 0.9130
Epoch 154/400
- 0s - loss: 1.1530 - acc: 0.8261
Epoch 155/400
- 0s - loss: 1.1432 - acc: 0.8261
Epoch 156/400
- 0s - loss: 1.1481 - acc: 0.8261
Epoch 157/400
- 0s - loss: 1.1401 - acc: 0.8696
Epoch 158/400
- 0s - loss: 1.1241 - acc: 0.8696
Epoch 159/400
- 0s - loss: 1.1240 - acc: 0.9130
Epoch 160/400
- 0s - loss: 1.1125 - acc: 0.9130
Epoch 161/400
- 0s - loss: 1.1103 - acc: 0.8696
Epoch 162/400
- 0s - loss: 1.1038 - acc: 0.8696
Epoch 163/400
- 0s - loss: 1.0996 - acc: 0.8696
Epoch 164/400
- 0s - loss: 1.0889 - acc: 0.8696
Epoch 165/400
- 0s - loss: 1.0917 - acc: 0.8261
Epoch 166/400
- 0s - loss: 1.0825 - acc: 0.8261
Epoch 167/400
- 0s - loss: 1.0885 - acc: 0.8261
Epoch 168/400
- 0s - loss: 1.0763 - acc: 0.8696
Epoch 169/400
- 0s - loss: 1.0647 - acc: 0.8696
Epoch 170/400
- 0s - loss: 1.0602 - acc: 0.8696
Epoch 171/400
- 0s - loss: 1.0542 - acc: 0.8696
Epoch 172/400
- 0s - loss: 1.0479 - acc: 0.8261
Epoch 173/400
- 0s - loss: 1.0519 - acc: 0.8696
Epoch 174/400
- 0s - loss: 1.0456 - acc: 0.9130
Epoch 175/400
- 0s - loss: 1.0316 - acc: 0.9130
Epoch 176/400
- 0s - loss: 1.0308 - acc: 0.9130
Epoch 177/400
- 0s - loss: 1.0253 - acc: 0.9130
Epoch 178/400
- 0s - loss: 1.0219 - acc: 0.9130
Epoch 179/400
- 0s - loss: 1.0136 - acc: 0.9130
Epoch 180/400
- 0s - loss: 1.0060 - acc: 0.9130
Epoch 181/400
- 0s - loss: 1.0015 - acc: 0.9130
Epoch 182/400
- 0s - loss: 1.0028 - acc: 0.8696
Epoch 183/400
- 0s - loss: 0.9979 - acc: 0.8696
Epoch 184/400
- 0s - loss: 0.9935 - acc: 0.9130
Epoch 185/400
- 0s - loss: 0.9851 - acc: 0.9130
Epoch 186/400
- 0s - loss: 0.9750 - acc: 0.8696
Epoch 187/400
- 0s - loss: 0.9704 - acc: 0.8696
Epoch 188/400
- 0s - loss: 0.9661 - acc: 0.9130
Epoch 189/400
- 0s - loss: 0.9695 - acc: 0.8696
Epoch 190/400
- 0s - loss: 0.9577 - acc: 0.9130
Epoch 191/400
- 0s - loss: 0.9603 - acc: 0.9130
Epoch 192/400
- 0s - loss: 0.9503 - acc: 0.9130
Epoch 193/400
- 0s - loss: 0.9416 - acc: 0.8696
Epoch 194/400
- 0s - loss: 0.9378 - acc: 0.9130
Epoch 195/400
- 0s - loss: 0.9346 - acc: 0.8696
Epoch 196/400
- 0s - loss: 0.9361 - acc: 0.9130
Epoch 197/400
- 0s - loss: 0.9275 - acc: 0.8261
Epoch 198/400
- 0s - loss: 0.9279 - acc: 0.8696
Epoch 199/400
- 0s - loss: 0.9258 - acc: 0.9130
Epoch 200/400
- 0s - loss: 0.9116 - acc: 0.9130
Epoch 201/400
- 0s - loss: 0.9087 - acc: 0.9130
Epoch 202/400
- 0s - loss: 0.9065 - acc: 0.8696
Epoch 203/400
- 0s - loss: 0.8957 - acc: 0.9130
Epoch 204/400
- 0s - loss: 0.8991 - acc: 0.9130
Epoch 205/400
- 0s - loss: 0.8937 - acc: 0.9130
Epoch 206/400
- 0s - loss: 0.8840 - acc: 0.9130
Epoch 207/400
- 0s - loss: 0.8844 - acc: 0.9130
Epoch 208/400
- 0s - loss: 0.8731 - acc: 0.9130
Epoch 209/400
- 0s - loss: 0.8804 - acc: 0.9130
Epoch 210/400
- 0s - loss: 0.8659 - acc: 0.9565
Epoch 211/400
- 0s - loss: 0.8685 - acc: 0.9565
Epoch 212/400
- 0s - loss: 0.8635 - acc: 0.9130
Epoch 213/400
- 0s - loss: 0.8611 - acc: 0.9130
Epoch 214/400
- 0s - loss: 0.8532 - acc: 0.9130
Epoch 215/400
- 0s - loss: 0.8483 - acc: 0.8696
Epoch 216/400
- 0s - loss: 0.8428 - acc: 0.8696
Epoch 217/400
- 0s - loss: 0.8376 - acc: 0.9130
Epoch 218/400
- 0s - loss: 0.8372 - acc: 0.9130
Epoch 219/400
- 0s - loss: 0.8347 - acc: 0.9130
Epoch 220/400
- 0s - loss: 0.8289 - acc: 0.8696
Epoch 221/400
- 0s - loss: 0.8210 - acc: 0.9565
Epoch 222/400
- 0s - loss: 0.8175 - acc: 0.9565
Epoch 223/400
- 0s - loss: 0.8194 - acc: 0.9130
Epoch 224/400
- 0s - loss: 0.8044 - acc: 0.8696
Epoch 225/400
- 0s - loss: 0.8063 - acc: 0.8696
Epoch 226/400
- 0s - loss: 0.8011 - acc: 0.9130
Epoch 227/400
- 0s - loss: 0.7963 - acc: 0.9130
Epoch 228/400
- 0s - loss: 0.7921 - acc: 0.9130
Epoch 229/400
- 0s - loss: 0.7878 - acc: 0.9130
Epoch 230/400
- 0s - loss: 0.7911 - acc: 0.8696
Epoch 231/400
- 0s - loss: 0.7852 - acc: 0.9130
Epoch 232/400
- 0s - loss: 0.7812 - acc: 0.9130
Epoch 233/400
- 0s - loss: 0.7741 - acc: 0.9130
Epoch 234/400
- 0s - loss: 0.7719 - acc: 0.8696
Epoch 235/400
- 0s - loss: 0.7711 - acc: 0.9130
Epoch 236/400
- 0s - loss: 0.7593 - acc: 0.9565
Epoch 237/400
- 0s - loss: 0.7581 - acc: 0.9130
Epoch 238/400
- 0s - loss: 0.7562 - acc: 0.9130
Epoch 239/400
- 0s - loss: 0.7577 - acc: 0.9130
Epoch 240/400
- 0s - loss: 0.7453 - acc: 0.8696
Epoch 241/400
- 0s - loss: 0.7404 - acc: 0.9130
Epoch 242/400
- 0s - loss: 0.7340 - acc: 0.9130
Epoch 243/400
- 0s - loss: 0.7358 - acc: 0.9565
Epoch 244/400
- 0s - loss: 0.7353 - acc: 0.9130
Epoch 245/400
- 0s - loss: 0.7353 - acc: 0.9565
Epoch 246/400
- 0s - loss: 0.7292 - acc: 0.9130
Epoch 247/400
- 0s - loss: 0.7270 - acc: 0.9565
Epoch 248/400
- 0s - loss: 0.7298 - acc: 0.9130
Epoch 249/400
- 0s - loss: 0.7172 - acc: 0.9130
Epoch 250/400
- 0s - loss: 0.7166 - acc: 0.9130
Epoch 251/400
- 0s - loss: 0.7117 - acc: 0.9565
Epoch 252/400
- 0s - loss: 0.7037 - acc: 0.9130
Epoch 253/400
- 0s - loss: 0.7029 - acc: 0.9565
Epoch 254/400
- 0s - loss: 0.6932 - acc: 0.9565
Epoch 255/400
- 0s - loss: 0.6989 - acc: 0.9130
Epoch 256/400
- 0s - loss: 0.6965 - acc: 0.9130
Epoch 257/400
- 0s - loss: 0.6896 - acc: 0.9130
Epoch 258/400
- 0s - loss: 0.6913 - acc: 0.9565
Epoch 259/400
- 0s - loss: 0.6849 - acc: 0.9130
Epoch 260/400
- 0s - loss: 0.6786 - acc: 0.9565
Epoch 261/400
- 0s - loss: 0.6836 - acc: 0.8696
Epoch 262/400
- 0s - loss: 0.6725 - acc: 0.8696
Epoch 263/400
- 0s - loss: 0.6712 - acc: 0.9130
Epoch 264/400
- 0s - loss: 0.6651 - acc: 0.9130
Epoch 265/400
- 0s - loss: 0.6574 - acc: 0.9565
Epoch 266/400
- 0s - loss: 0.6620 - acc: 0.9130
Epoch 267/400
- 0s - loss: 0.6564 - acc: 0.9565
Epoch 268/400
- 0s - loss: 0.6523 - acc: 0.9565
Epoch 269/400
- 0s - loss: 0.6537 - acc: 0.9130
Epoch 270/400
- 0s - loss: 0.6547 - acc: 0.9565
Epoch 271/400
- 0s - loss: 0.6499 - acc: 0.9130
Epoch 272/400
- 0s - loss: 0.6469 - acc: 0.8696
Epoch 273/400
- 0s - loss: 0.6391 - acc: 0.9565
Epoch 274/400
- 0s - loss: 0.6390 - acc: 0.9565
Epoch 275/400
- 0s - loss: 0.6343 - acc: 0.9130
Epoch 276/400
- 0s - loss: 0.6300 - acc: 0.9130
Epoch 277/400
- 0s - loss: 0.6300 - acc: 0.9565
Epoch 278/400
- 0s - loss: 0.6331 - acc: 0.9130
Epoch 279/400
- 0s - loss: 0.6311 - acc: 0.9130
Epoch 280/400
- 0s - loss: 0.6272 - acc: 0.9130
Epoch 281/400
- 0s - loss: 0.6205 - acc: 0.9130
Epoch 282/400
- 0s - loss: 0.6135 - acc: 0.9130
Epoch 283/400
- 0s - loss: 0.6132 - acc: 0.9130
Epoch 284/400
- 0s - loss: 0.6079 - acc: 0.9565
Epoch 285/400
- 0s - loss: 0.6115 - acc: 0.9130
Epoch 286/400
- 0s - loss: 0.6090 - acc: 0.8696
Epoch 287/400
- 0s - loss: 0.6026 - acc: 0.9130
Epoch 288/400
- 0s - loss: 0.5981 - acc: 0.9130
Epoch 289/400
- 0s - loss: 0.5947 - acc: 0.9565
Epoch 290/400
- 0s - loss: 0.5904 - acc: 0.9130
Epoch 291/400
- 0s - loss: 0.5904 - acc: 0.9130
Epoch 292/400
- 0s - loss: 0.5871 - acc: 0.9130
Epoch 293/400
- 0s - loss: 0.5827 - acc: 0.9130
Epoch 294/400
- 0s - loss: 0.5773 - acc: 0.9130
Epoch 295/400
- 0s - loss: 0.5772 - acc: 0.9130
Epoch 296/400
- 0s - loss: 0.5729 - acc: 0.9565
Epoch 297/400
- 0s - loss: 0.5747 - acc: 0.9130
Epoch 298/400
- 0s - loss: 0.5716 - acc: 0.8696
Epoch 299/400
- 0s - loss: 0.5679 - acc: 0.9130
Epoch 300/400
- 0s - loss: 0.5679 - acc: 0.9565
Epoch 301/400
- 0s - loss: 0.5658 - acc: 0.9565
Epoch 302/400
- 0s - loss: 0.5644 - acc: 0.9565
Epoch 303/400
- 0s - loss: 0.5600 - acc: 0.9565
Epoch 304/400
- 0s - loss: 0.5549 - acc: 0.9565
Epoch 305/400
- 0s - loss: 0.5510 - acc: 0.9565
Epoch 306/400
- 0s - loss: 0.5513 - acc: 0.9565
Epoch 307/400
- 0s - loss: 0.5472 - acc: 0.9565
Epoch 308/400
- 0s - loss: 0.5464 - acc: 0.9130
Epoch 309/400
- 0s - loss: 0.5446 - acc: 0.8696
Epoch 310/400
- 0s - loss: 0.5411 - acc: 0.9565
Epoch 311/400
- 0s - loss: 0.5372 - acc: 0.9565
Epoch 312/400
- 0s - loss: 0.5379 - acc: 0.9130
Epoch 313/400
- 0s - loss: 0.5337 - acc: 0.9130
Epoch 314/400
- 0s - loss: 0.5371 - acc: 0.9130
Epoch 315/400
- 0s - loss: 0.5290 - acc: 0.9130
Epoch 316/400
- 0s - loss: 0.5274 - acc: 0.9130
Epoch 317/400
- 0s - loss: 0.5197 - acc: 0.8696
Epoch 318/400
- 0s - loss: 0.5299 - acc: 0.9130
Epoch 319/400
- 0s - loss: 0.5251 - acc: 0.9565
Epoch 320/400
- 0s - loss: 0.5215 - acc: 0.9130
Epoch 321/400
- 0s - loss: 0.5203 - acc: 0.9565
Epoch 322/400
- 0s - loss: 0.5182 - acc: 0.9130
Epoch 323/400
- 0s - loss: 0.5135 - acc: 0.9565
Epoch 324/400
- 0s - loss: 0.5142 - acc: 0.8696
Epoch 325/400
- 0s - loss: 0.5101 - acc: 0.9565
Epoch 326/400
- 0s - loss: 0.5012 - acc: 0.9565
Epoch 327/400
- 0s - loss: 0.5000 - acc: 0.9565
Epoch 328/400
- 0s - loss: 0.4999 - acc: 0.9565
Epoch 329/400
- 0s - loss: 0.4978 - acc: 0.9565
Epoch 330/400
- 0s - loss: 0.4955 - acc: 0.9130
Epoch 331/400
- 0s - loss: 0.4916 - acc: 0.9130
Epoch 332/400
- 0s - loss: 0.4904 - acc: 0.9565
Epoch 333/400
- 0s - loss: 0.4870 - acc: 0.9130
Epoch 334/400
- 0s - loss: 0.4878 - acc: 0.9130
Epoch 335/400
- 0s - loss: 0.4846 - acc: 0.9130
Epoch 336/400
- 0s - loss: 0.4838 - acc: 0.8696
Epoch 337/400
- 0s - loss: 0.4833 - acc: 0.9130
Epoch 338/400
- 0s - loss: 0.4807 - acc: 0.8696
Epoch 339/400
- 0s - loss: 0.4764 - acc: 0.9130
Epoch 340/400
- 0s - loss: 0.4760 - acc: 0.9565
Epoch 341/400
- 0s - loss: 0.4800 - acc: 0.9130
Epoch 342/400
- 0s - loss: 0.4741 - acc: 0.9565
Epoch 343/400
- 0s - loss: 0.4706 - acc: 1.0000
Epoch 344/400
- 0s - loss: 0.4670 - acc: 1.0000
Epoch 345/400
- 0s - loss: 0.4660 - acc: 0.9130
Epoch 346/400
- 0s - loss: 0.4626 - acc: 0.9130
Epoch 347/400
- 0s - loss: 0.4616 - acc: 0.9130
Epoch 348/400
- 0s - loss: 0.4610 - acc: 0.9565
Epoch 349/400
- 0s - loss: 0.4540 - acc: 0.9130
Epoch 350/400
- 0s - loss: 0.4575 - acc: 0.9565
Epoch 351/400
- 0s - loss: 0.4511 - acc: 0.9565
Epoch 352/400
- 0s - loss: 0.4551 - acc: 0.9130
Epoch 353/400
- 0s - loss: 0.4520 - acc: 0.9565
Epoch 354/400
- 0s - loss: 0.4468 - acc: 0.9565
Epoch 355/400
- 0s - loss: 0.4560 - acc: 0.9565
Epoch 356/400
- 0s - loss: 0.4442 - acc: 0.9565
Epoch 357/400
- 0s - loss: 0.4432 - acc: 0.9130
Epoch 358/400
- 0s - loss: 0.4408 - acc: 0.9130
Epoch 359/400
- 0s - loss: 0.4396 - acc: 0.9565
Epoch 360/400
- 0s - loss: 0.4364 - acc: 0.9565
Epoch 361/400
- 0s - loss: 0.4306 - acc: 0.9565
Epoch 362/400
- 0s - loss: 0.4337 - acc: 0.9565
Epoch 363/400
- 0s - loss: 0.4315 - acc: 0.9565
Epoch 364/400
- 0s - loss: 0.4252 - acc: 0.9565
Epoch 365/400
- 0s - loss: 0.4291 - acc: 0.9565
Epoch 366/400
- 0s - loss: 0.4274 - acc: 0.9130
Epoch 367/400
- 0s - loss: 0.4264 - acc: 0.9130
Epoch 368/400
- 0s - loss: 0.4245 - acc: 0.9130
Epoch 369/400
- 0s - loss: 0.4270 - acc: 0.9565
Epoch 370/400
- 0s - loss: 0.4252 - acc: 0.9130
Epoch 371/400
- 0s - loss: 0.4296 - acc: 1.0000
Epoch 372/400
- 0s - loss: 0.4262 - acc: 0.9565
Epoch 373/400
- 0s - loss: 0.4189 - acc: 0.9565
Epoch 374/400
- 0s - loss: 0.4171 - acc: 0.9130
Epoch 375/400
- 0s - loss: 0.4085 - acc: 0.9130
Epoch 376/400
- 0s - loss: 0.4077 - acc: 0.9565
Epoch 377/400
- 0s - loss: 0.4039 - acc: 0.9565
Epoch 378/400
- 0s - loss: 0.4024 - acc: 0.9565
Epoch 379/400
- 0s - loss: 0.4016 - acc: 0.9565
Epoch 380/400
- 0s - loss: 0.4024 - acc: 0.9130
Epoch 381/400
- 0s - loss: 0.3991 - acc: 1.0000
Epoch 382/400
- 0s - loss: 0.3974 - acc: 0.9565
Epoch 383/400
- 0s - loss: 0.3954 - acc: 0.9130
Epoch 384/400
- 0s - loss: 0.3988 - acc: 0.9565
Epoch 385/400
- 0s - loss: 0.3927 - acc: 0.9565
Epoch 386/400
- 0s - loss: 0.3928 - acc: 1.0000
Epoch 387/400
- 0s - loss: 0.3945 - acc: 1.0000
Epoch 388/400
- 0s - loss: 0.3926 - acc: 0.9565
Epoch 389/400
- 0s - loss: 0.3907 - acc: 0.9130
Epoch 390/400
- 0s - loss: 0.3883 - acc: 0.9565
Epoch 391/400
- 0s - loss: 0.3824 - acc: 0.9130
Epoch 392/400
- 0s - loss: 0.3811 - acc: 0.9565
Epoch 393/400
- 0s - loss: 0.3794 - acc: 0.9565
Epoch 394/400
- 0s - loss: 0.3830 - acc: 0.9565
Epoch 395/400
- 0s - loss: 0.3786 - acc: 1.0000
Epoch 396/400
- 0s - loss: 0.3767 - acc: 1.0000
Epoch 397/400
- 0s - loss: 0.3764 - acc: 0.9565
Epoch 398/400
- 0s - loss: 0.3751 - acc: 0.9565
Epoch 399/400
- 0s - loss: 0.3719 - acc: 1.0000
Epoch 400/400
- 0s - loss: 0.3684 - acc: 1.0000
23/23 [==============================] - 0s 4ms/step
Model Accuracy: 100.00%
['W', 'B', 'C'] -> Z
['W', 'K', 'L'] -> Z
['W', 'T', 'U'] -> Z
['D', 'W', 'F'] -> I
['M', 'W', 'O'] -> Q
['V', 'W', 'W'] -> Y
['G', 'H', 'W'] -> J
['J', 'K', 'W'] -> M
['P', 'Q', 'W'] -> S
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
'''Example script to generate text from Nietzsche's writings.
At least 20 epochs are required before the generated text
starts sounding coherent.
It is recommended to run this script on GPU, as recurrent
networks are quite computationally intensive.
If you try this script on new data, make sure your corpus
has at least ~100k characters. ~1M is better.
'''
from __future__ import print_function
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LSTM
from keras.optimizers import RMSprop
from keras.utils.data_utils import get_file
import numpy as np
import random
import sys
path = get_file('nietzsche.txt', origin='https://s3.amazonaws.com/text-datasets/nietzsche.txt')
text = open(path).read().lower()
print('corpus length:', len(text))
chars = sorted(list(set(text)))
print('total chars:', len(chars))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))
# cut the text in semi-redundant sequences of maxlen characters
maxlen = 40
step = 3
sentences = []
next_chars = []
for i in range(0, len(text) - maxlen, step):
sentences.append(text[i: i + maxlen])
next_chars.append(text[i + maxlen])
print('nb sequences:', len(sentences))
print('Vectorization...')
X = np.zeros((len(sentences), maxlen, len(chars)), dtype=np.bool)
y = np.zeros((len(sentences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(sentences):
for t, char in enumerate(sentence):
X[i, t, char_indices[char]] = 1
y[i, char_indices[next_chars[i]]] = 1
# build the model: a single LSTM
print('Build model...')
model = Sequential()
model.add(LSTM(128, input_shape=(maxlen, len(chars))))
model.add(Dense(len(chars)))
model.add(Activation('softmax'))
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
def sample(preds, temperature=1.0):
# helper function to sample an index from a probability array
preds = np.asarray(preds).astype('float64')
preds = np.log(preds) / temperature
exp_preds = np.exp(preds)
preds = exp_preds / np.sum(exp_preds)
probas = np.random.multinomial(1, preds, 1)
return np.argmax(probas)
# train the model, output generated text after each iteration
for iteration in range(1, 60):
print()
print('-' * 50)
print('Iteration', iteration)
model.fit(X, y,
batch_size=128,
epochs=1)
start_index = random.randint(0, len(text) - maxlen - 1)
for diversity in [0.2, 0.5, 1.0, 1.2]:
print()
print('----- diversity:', diversity)
generated = ''
sentence = text[start_index: start_index + maxlen]
generated += sentence
print('----- Generating with seed: "' + sentence + '"')
sys.stdout.write(generated)
for i in range(400):
x = np.zeros((1, maxlen, len(chars)))
for t, char in enumerate(sentence):
x[0, t, char_indices[char]] = 1.
preds = model.predict(x, verbose=0)[0]
next_index = sample(preds, diversity)
next_char = indices_char[next_index]
generated += next_char
sentence = sentence[1:] + next_char
sys.stdout.write(next_char)
sys.stdout.flush()
print()
Using TensorFlow backend.
Downloading data from https://s3.amazonaws.com/text-datasets/nietzsche.txt
8192/600901 [..............................] - ETA: 5s
57344/600901 [=>............................] - ETA: 1s
90112/600901 [===>..........................] - ETA: 1s
131072/600901 [=====>........................] - ETA: 1s
180224/600901 [=======>......................] - ETA: 0s
212992/600901 [=========>....................] - ETA: 0s
245760/600901 [===========>..................] - ETA: 0s
319488/600901 [==============>...............] - ETA: 0s
475136/600901 [======================>.......] - ETA: 0s
606208/600901 [==============================] - 1s 1us/step
corpus length: 600893
total chars: 57
nb sequences: 200285
Vectorization...
Build model...
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
--------------------------------------------------
Iteration 1
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Epoch 1/1
128/200285 [..............................] - ETA: 1:51:43 - loss: 4.0438
256/200285 [..............................] - ETA: 1:01:34 - loss: 3.8643
384/200285 [..............................] - ETA: 44:38 - loss: 3.9969
512/200285 [..............................] - ETA: 35:53 - loss: 3.9730
640/200285 [..............................] - ETA: 30:43 - loss: 3.8894
768/200285 [..............................] - ETA: 27:27 - loss: 3.7772
896/200285 [..............................] - ETA: 24:54 - loss: 3.6588
1024/200285 [..............................] - ETA: 22:58 - loss: 3.5957
1152/200285 [..............................] - ETA: 21:24 - loss: 3.5234
1280/200285 [..............................] - ETA: 20:14 - loss: 3.4729
1408/200285 [..............................] - ETA: 19:14 - loss: 3.4467
1536/200285 [..............................] - ETA: 18:29 - loss: 3.4135
1664/200285 [..............................] - ETA: 17:46 - loss: 3.3925
1792/200285 [..............................] - ETA: 17:10 - loss: 3.3634
1920/200285 [..............................] - ETA: 16:43 - loss: 3.3300
2048/200285 [..............................] - ETA: 16:26 - loss: 3.3182
2176/200285 [..............................] - ETA: 16:04 - loss: 3.2964
2304/200285 [..............................] - ETA: 15:45 - loss: 3.2769
2432/200285 [..............................] - ETA: 15:24 - loss: 3.2639
2560/200285 [..............................] - ETA: 15:02 - loss: 3.2490
2688/200285 [..............................] - ETA: 14:44 - loss: 3.2349
2816/200285 [..............................] - ETA: 14:36 - loss: 3.2276
2944/200285 [..............................] - ETA: 14:27 - loss: 3.2195
3072/200285 [..............................] - ETA: 14:17 - loss: 3.2163
3200/200285 [..............................] - ETA: 14:03 - loss: 3.2052
3328/200285 [..............................] - ETA: 13:53 - loss: 3.1999
3456/200285 [..............................] - ETA: 13:49 - loss: 3.1922
3584/200285 [..............................] - ETA: 13:44 - loss: 3.1859
3712/200285 [..............................] - ETA: 13:40 - loss: 3.1801
3840/200285 [..............................] - ETA: 13:33 - loss: 3.1739
3968/200285 [..............................] - ETA: 13:27 - loss: 3.1672
4096/200285 [..............................] - ETA: 13:21 - loss: 3.1585
4224/200285 [..............................] - ETA: 13:18 - loss: 3.1521
4352/200285 [..............................] - ETA: 13:13 - loss: 3.1484
4480/200285 [..............................] - ETA: 13:10 - loss: 3.1393
4608/200285 [..............................] - ETA: 13:07 - loss: 3.1348
4736/200285 [..............................] - ETA: 13:05 - loss: 3.1296
4864/200285 [..............................] - ETA: 13:01 - loss: 3.1216
4992/200285 [..............................] - ETA: 12:57 - loss: 3.1132
5120/200285 [..............................] - ETA: 12:51 - loss: 3.1076
5248/200285 [..............................] - ETA: 12:46 - loss: 3.1005
5376/200285 [..............................] - ETA: 12:40 - loss: 3.0970
5504/200285 [..............................] - ETA: 12:36 - loss: 3.0924
5632/200285 [..............................] - ETA: 12:31 - loss: 3.0858
5760/200285 [..............................] - ETA: 12:27 - loss: 3.0794
5888/200285 [..............................] - ETA: 12:24 - loss: 3.0728
6016/200285 [..............................] - ETA: 12:21 - loss: 3.0695
6144/200285 [..............................] - ETA: 12:18 - loss: 3.0679
6272/200285 [..............................] - ETA: 12:15 - loss: 3.0609
6400/200285 [..............................] - ETA: 12:14 - loss: 3.0523
6528/200285 [..............................] - ETA: 12:15 - loss: 3.0485
6656/200285 [..............................] - ETA: 12:13 - loss: 3.0431
6784/200285 [>.............................] - ETA: 12:11 - loss: 3.0397
6912/200285 [>.............................] - ETA: 12:08 - loss: 3.0348
7040/200285 [>.............................] - ETA: 12:06 - loss: 3.0265
7168/200285 [>.............................] - ETA: 12:02 - loss: 3.0215
7296/200285 [>.............................] - ETA: 12:00 - loss: 3.0153
7424/200285 [>.............................] - ETA: 11:57 - loss: 3.0066
7552/200285 [>.............................] - ETA: 11:55 - loss: 3.0044
7680/200285 [>.............................] - ETA: 11:53 - loss: 2.9986
7808/200285 [>.............................] - ETA: 11:49 - loss: 2.9911
7936/200285 [>.............................] - ETA: 11:47 - loss: 2.9867
8064/200285 [>.............................] - ETA: 11:47 - loss: 2.9814
8192/200285 [>.............................] - ETA: 11:47 - loss: 2.9778
8320/200285 [>.............................] - ETA: 11:47 - loss: 2.9721
8448/200285 [>.............................] - ETA: 11:44 - loss: 2.9666
8576/200285 [>.............................] - ETA: 11:40 - loss: 2.9609
8704/200285 [>.............................] - ETA: 11:37 - loss: 2.9548
8832/200285 [>.............................] - ETA: 11:34 - loss: 2.9480
8960/200285 [>.............................] - ETA: 11:34 - loss: 2.9429
9088/200285 [>.............................] - ETA: 11:31 - loss: 2.9380
9216/200285 [>.............................] - ETA: 11:30 - loss: 2.9321
9344/200285 [>.............................] - ETA: 11:27 - loss: 2.9302
9472/200285 [>.............................] - ETA: 11:25 - loss: 2.9251
9600/200285 [>.............................] - ETA: 11:21 - loss: 2.9223
9728/200285 [>.............................] - ETA: 11:18 - loss: 2.9175
9856/200285 [>.............................] - ETA: 11:14 - loss: 2.9115
9984/200285 [>.............................] - ETA: 11:12 - loss: 2.9070
10112/200285 [>.............................] - ETA: 11:09 - loss: 2.9050
10240/200285 [>.............................] - ETA: 11:07 - loss: 2.9000
10368/200285 [>.............................] - ETA: 11:05 - loss: 2.8975
10496/200285 [>.............................] - ETA: 11:03 - loss: 2.8965
10624/200285 [>.............................] - ETA: 11:02 - loss: 2.8910
10752/200285 [>.............................] - ETA: 10:59 - loss: 2.8852
10880/200285 [>.............................] - ETA: 10:58 - loss: 2.8817
11008/200285 [>.............................] - ETA: 10:56 - loss: 2.8773
11136/200285 [>.............................] - ETA: 10:55 - loss: 2.8748
11264/200285 [>.............................] - ETA: 10:54 - loss: 2.8674
11392/200285 [>.............................] - ETA: 10:55 - loss: 2.8634
11520/200285 [>.............................] - ETA: 10:52 - loss: 2.8604
11648/200285 [>.............................] - ETA: 10:52 - loss: 2.8592
11776/200285 [>.............................] - ETA: 10:50 - loss: 2.8572
11904/200285 [>.............................] - ETA: 10:49 - loss: 2.8543
12032/200285 [>.............................] - ETA: 10:48 - loss: 2.8495
12160/200285 [>.............................] - ETA: 10:46 - loss: 2.8447
12288/200285 [>.............................] - ETA: 10:46 - loss: 2.8409
12416/200285 [>.............................] - ETA: 10:45 - loss: 2.8376
12544/200285 [>.............................] - ETA: 10:45 - loss: 2.8351
12672/200285 [>.............................] - ETA: 10:44 - loss: 2.8321
12800/200285 [>.............................] - ETA: 10:42 - loss: 2.8289
12928/200285 [>.............................] - ETA: 10:41 - loss: 2.8260
13056/200285 [>.............................] - ETA: 10:40 - loss: 2.8218
13184/200285 [>.............................] - ETA: 10:39 - loss: 2.8206
13312/200285 [>.............................] - ETA: 10:38 - loss: 2.8176
13440/200285 [=>............................] - ETA: 10:37 - loss: 2.8165
13568/200285 [=>............................] - ETA: 10:35 - loss: 2.8143
13696/200285 [=>............................] - ETA: 10:33 - loss: 2.8116
13824/200285 [=>............................] - ETA: 10:32 - loss: 2.8085
13952/200285 [=>............................] - ETA: 10:31 - loss: 2.8068
14080/200285 [=>............................] - ETA: 10:29 - loss: 2.8046
14208/200285 [=>............................] - ETA: 10:27 - loss: 2.8014
14336/200285 [=>............................] - ETA: 10:26 - loss: 2.7968
14464/200285 [=>............................] - ETA: 10:24 - loss: 2.7946
14592/200285 [=>............................] - ETA: 10:23 - loss: 2.7926
14720/200285 [=>............................] - ETA: 10:22 - loss: 2.7902
14848/200285 [=>............................] - ETA: 10:21 - loss: 2.7875
14976/200285 [=>............................] - ETA: 10:19 - loss: 2.7851
15104/200285 [=>............................] - ETA: 10:18 - loss: 2.7817
15232/200285 [=>............................] - ETA: 10:17 - loss: 2.7773
15360/200285 [=>............................] - ETA: 10:16 - loss: 2.7751
15488/200285 [=>............................] - ETA: 10:15 - loss: 2.7699
15616/200285 [=>............................] - ETA: 10:14 - loss: 2.7669
15744/200285 [=>............................] - ETA: 10:13 - loss: 2.7667
15872/200285 [=>............................] - ETA: 10:12 - loss: 2.7642
16000/200285 [=>............................] - ETA: 10:11 - loss: 2.7626
16128/200285 [=>............................] - ETA: 10:11 - loss: 2.7602
16256/200285 [=>............................] - ETA: 10:09 - loss: 2.7582
16384/200285 [=>............................] - ETA: 10:08 - loss: 2.7564
16512/200285 [=>............................] - ETA: 10:08 - loss: 2.7554
16640/200285 [=>............................] - ETA: 10:06 - loss: 2.7538
16768/200285 [=>............................] - ETA: 10:04 - loss: 2.7505
16896/200285 [=>............................] - ETA: 10:03 - loss: 2.7482
17024/200285 [=>............................] - ETA: 10:02 - loss: 2.7448
17152/200285 [=>............................] - ETA: 10:02 - loss: 2.7432
17280/200285 [=>............................] - ETA: 10:01 - loss: 2.7406
17408/200285 [=>............................] - ETA: 10:01 - loss: 2.7382
17536/200285 [=>............................] - ETA: 10:00 - loss: 2.7364
17664/200285 [=>............................] - ETA: 9:58 - loss: 2.7329
17792/200285 [=>............................] - ETA: 9:57 - loss: 2.7311
17920/200285 [=>............................] - ETA: 9:55 - loss: 2.7303
18048/200285 [=>............................] - ETA: 9:55 - loss: 2.7282
18176/200285 [=>............................] - ETA: 9:54 - loss: 2.7259
18304/200285 [=>............................] - ETA: 9:54 - loss: 2.7232
18432/200285 [=>............................] - ETA: 9:53 - loss: 2.7217
18560/200285 [=>............................] - ETA: 9:52 - loss: 2.7170
18688/200285 [=>............................] - ETA: 9:51 - loss: 2.7141
18816/200285 [=>............................] - ETA: 9:50 - loss: 2.7135
18944/200285 [=>............................] - ETA: 9:49 - loss: 2.7122
19072/200285 [=>............................] - ETA: 9:48 - loss: 2.7103
19200/200285 [=>............................] - ETA: 9:48 - loss: 2.7078
19328/200285 [=>............................] - ETA: 9:47 - loss: 2.7055
19456/200285 [=>............................] - ETA: 9:46 - loss: 2.7028
19584/200285 [=>............................] - ETA: 9:46 - loss: 2.6997
19712/200285 [=>............................] - ETA: 9:46 - loss: 2.6988
19840/200285 [=>............................] - ETA: 9:45 - loss: 2.6967
19968/200285 [=>............................] - ETA: 9:46 - loss: 2.6941
20096/200285 [==>...........................] - ETA: 9:44 - loss: 2.6908
20224/200285 [==>...........................] - ETA: 9:44 - loss: 2.6879
20352/200285 [==>...........................] - ETA: 9:43 - loss: 2.6862
20480/200285 [==>...........................] - ETA: 9:42 - loss: 2.6839
20608/200285 [==>...........................] - ETA: 9:41 - loss: 2.6819
20736/200285 [==>...........................] - ETA: 9:40 - loss: 2.6797
20864/200285 [==>...........................] - ETA: 9:40 - loss: 2.6774
20992/200285 [==>...........................] - ETA: 9:40 - loss: 2.6767
21120/200285 [==>...........................] - ETA: 9:40 - loss: 2.6748
21248/200285 [==>...........................] - ETA: 9:40 - loss: 2.6727
21376/200285 [==>...........................] - ETA: 9:39 - loss: 2.6715
21504/200285 [==>...........................] - ETA: 9:40 - loss: 2.6692
21632/200285 [==>...........................] - ETA: 9:39 - loss: 2.6660
21760/200285 [==>...........................] - ETA: 9:39 - loss: 2.6641
21888/200285 [==>...........................] - ETA: 9:39 - loss: 2.6622
22016/200285 [==>...........................] - ETA: 9:39 - loss: 2.6594
22144/200285 [==>...........................] - ETA: 9:39 - loss: 2.6577
22272/200285 [==>...........................] - ETA: 9:39 - loss: 2.6561
22400/200285 [==>...........................] - ETA: 9:38 - loss: 2.6540
22528/200285 [==>...........................] - ETA: 9:38 - loss: 2.6515
22656/200285 [==>...........................] - ETA: 9:37 - loss: 2.6492
22784/200285 [==>...........................] - ETA: 9:36 - loss: 2.6479
22912/200285 [==>...........................] - ETA: 9:36 - loss: 2.6461
23040/200285 [==>...........................] - ETA: 9:35 - loss: 2.6446
23168/200285 [==>...........................] - ETA: 9:35 - loss: 2.6429
23296/200285 [==>...........................] - ETA: 9:35 - loss: 2.6408
23424/200285 [==>...........................] - ETA: 9:35 - loss: 2.6399
23552/200285 [==>...........................] - ETA: 9:35 - loss: 2.6381
23680/200285 [==>...........................] - ETA: 9:35 - loss: 2.6360
23808/200285 [==>...........................] - ETA: 9:35 - loss: 2.6343
23936/200285 [==>...........................] - ETA: 9:35 - loss: 2.6318
24064/200285 [==>...........................] - ETA: 9:35 - loss: 2.6306
24192/200285 [==>...........................] - ETA: 9:36 - loss: 2.6285
24320/200285 [==>...........................] - ETA: 9:35 - loss: 2.6267
24448/200285 [==>...........................] - ETA: 9:35 - loss: 2.6251
24576/200285 [==>...........................] - ETA: 9:35 - loss: 2.6239
24704/200285 [==>...........................] - ETA: 9:36 - loss: 2.6219
24832/200285 [==>...........................] - ETA: 9:36 - loss: 2.6210
24960/200285 [==>...........................] - ETA: 9:36 - loss: 2.6195
25088/200285 [==>...........................] - ETA: 9:36 - loss: 2.6176
25216/200285 [==>...........................] - ETA: 9:36 - loss: 2.6155
25344/200285 [==>...........................] - ETA: 9:36 - loss: 2.6139
25472/200285 [==>...........................] - ETA: 9:36 - loss: 2.6114
25600/200285 [==>...........................] - ETA: 9:36 - loss: 2.6103
25728/200285 [==>...........................] - ETA: 9:36 - loss: 2.6082
25856/200285 [==>...........................] - ETA: 9:35 - loss: 2.6064
25984/200285 [==>...........................] - ETA: 9:35 - loss: 2.6059
26112/200285 [==>...........................] - ETA: 9:35 - loss: 2.6043
26240/200285 [==>...........................] - ETA: 9:36 - loss: 2.6022
26368/200285 [==>...........................] - ETA: 9:36 - loss: 2.6003
26496/200285 [==>...........................] - ETA: 9:37 - loss: 2.5979
26624/200285 [==>...........................] - ETA: 9:36 - loss: 2.5975
26752/200285 [===>..........................] - ETA: 9:35 - loss: 2.5962
26880/200285 [===>..........................] - ETA: 9:35 - loss: 2.5947
27008/200285 [===>..........................] - ETA: 9:35 - loss: 2.5935
27136/200285 [===>..........................] - ETA: 9:34 - loss: 2.5911
27264/200285 [===>..........................] - ETA: 9:34 - loss: 2.5894
27392/200285 [===>..........................] - ETA: 9:33 - loss: 2.5876
27520/200285 [===>..........................] - ETA: 9:34 - loss: 2.5853
27648/200285 [===>..........................] - ETA: 9:34 - loss: 2.5825
27776/200285 [===>..........................] - ETA: 9:33 - loss: 2.5817
27904/200285 [===>..........................] - ETA: 9:33 - loss: 2.5798
28032/200285 [===>..........................] - ETA: 9:32 - loss: 2.5779
28160/200285 [===>..........................] - ETA: 9:32 - loss: 2.5755
28288/200285 [===>..........................] - ETA: 9:32 - loss: 2.5746
28416/200285 [===>..........................] - ETA: 9:32 - loss: 2.5738
28544/200285 [===>..........................] - ETA: 9:31 - loss: 2.5722
28672/200285 [===>..........................] - ETA: 9:31 - loss: 2.5703
28800/200285 [===>..........................] - ETA: 9:31 - loss: 2.5683
28928/200285 [===>..........................] - ETA: 9:31 - loss: 2.5675
29056/200285 [===>..........................] - ETA: 9:31 - loss: 2.5655
29184/200285 [===>..........................] - ETA: 9:30 - loss: 2.5635
29312/200285 [===>..........................] - ETA: 9:30 - loss: 2.5617
29440/200285 [===>..........................] - ETA: 9:30 - loss: 2.5618
29568/200285 [===>..........................] - ETA: 9:30 - loss: 2.5601
29696/200285 [===>..........................] - ETA: 9:29 - loss: 2.5579
29824/200285 [===>..........................] - ETA: 9:29 - loss: 2.5570
29952/200285 [===>..........................] - ETA: 9:29 - loss: 2.5559
30080/200285 [===>..........................] - ETA: 9:29 - loss: 2.5553
30208/200285 [===>..........................] - ETA: 9:29 - loss: 2.5537
30336/200285 [===>..........................] - ETA: 9:28 - loss: 2.5528
30464/200285 [===>..........................] - ETA: 9:29 - loss: 2.5515
30592/200285 [===>..........................] - ETA: 9:28 - loss: 2.5503
30720/200285 [===>..........................] - ETA: 9:27 - loss: 2.5485
30848/200285 [===>..........................] - ETA: 9:27 - loss: 2.5464
30976/200285 [===>..........................] - ETA: 9:27 - loss: 2.5438
31104/200285 [===>..........................] - ETA: 9:26 - loss: 2.5423
31232/200285 [===>..........................] - ETA: 9:26 - loss: 2.5415
31360/200285 [===>..........................] - ETA: 9:25 - loss: 2.5398
31488/200285 [===>..........................] - ETA: 9:25 - loss: 2.5382
31616/200285 [===>..........................] - ETA: 9:24 - loss: 2.5363
31744/200285 [===>..........................] - ETA: 9:23 - loss: 2.5345
31872/200285 [===>..........................] - ETA: 9:23 - loss: 2.5326
32000/200285 [===>..........................] - ETA: 9:22 - loss: 2.5316
32128/200285 [===>..........................] - ETA: 9:21 - loss: 2.5298
32256/200285 [===>..........................] - ETA: 9:21 - loss: 2.5282
32384/200285 [===>..........................] - ETA: 9:21 - loss: 2.5269
32512/200285 [===>..........................] - ETA: 9:21 - loss: 2.5256
32640/200285 [===>..........................] - ETA: 9:20 - loss: 2.5244
32768/200285 [===>..........................] - ETA: 9:20 - loss: 2.5224
32896/200285 [===>..........................] - ETA: 9:20 - loss: 2.5212
33024/200285 [===>..........................] - ETA: 9:19 - loss: 2.5203
33152/200285 [===>..........................] - ETA: 9:19 - loss: 2.5182
33280/200285 [===>..........................] - ETA: 9:20 - loss: 2.5168
33408/200285 [====>.........................] - ETA: 9:19 - loss: 2.5156
33536/200285 [====>.........................] - ETA: 9:19 - loss: 2.5142
33664/200285 [====>.........................] - ETA: 9:19 - loss: 2.5122
33792/200285 [====>.........................] - ETA: 9:19 - loss: 2.5109
33920/200285 [====>.........................] - ETA: 9:18 - loss: 2.5090
34048/200285 [====>.........................] - ETA: 9:18 - loss: 2.5078
34176/200285 [====>.........................] - ETA: 9:18 - loss: 2.5066
34304/200285 [====>.........................] - ETA: 9:18 - loss: 2.5055
34432/200285 [====>.........................] - ETA: 9:17 - loss: 2.5048
34560/200285 [====>.........................] - ETA: 9:17 - loss: 2.5041
34688/200285 [====>.........................] - ETA: 9:16 - loss: 2.5030
34816/200285 [====>.........................] - ETA: 9:16 - loss: 2.5018
34944/200285 [====>.........................] - ETA: 9:15 - loss: 2.5007
35072/200285 [====>.........................] - ETA: 9:15 - loss: 2.4992
35200/200285 [====>.........................] - ETA: 9:14 - loss: 2.4981
35328/200285 [====>.........................] - ETA: 9:14 - loss: 2.4972
35456/200285 [====>.........................] - ETA: 9:14 - loss: 2.4964
35584/200285 [====>.........................] - ETA: 9:14 - loss: 2.4942
35712/200285 [====>.........................] - ETA: 9:13 - loss: 2.4930
35840/200285 [====>.........................] - ETA: 9:13 - loss: 2.4912
35968/200285 [====>.........................] - ETA: 9:12 - loss: 2.4906
36096/200285 [====>.........................] - ETA: 9:12 - loss: 2.4893
36224/200285 [====>.........................] - ETA: 9:11 - loss: 2.4895
36352/200285 [====>.........................] - ETA: 9:11 - loss: 2.4886
36480/200285 [====>.........................] - ETA: 9:10 - loss: 2.4877
36608/200285 [====>.........................] - ETA: 9:10 - loss: 2.4867
36736/200285 [====>.........................] - ETA: 9:10 - loss: 2.4854
36864/200285 [====>.........................] - ETA: 9:09 - loss: 2.4844
36992/200285 [====>.........................] - ETA: 9:09 - loss: 2.4829
37120/200285 [====>.........................] - ETA: 9:08 - loss: 2.4818
37248/200285 [====>.........................] - ETA: 9:08 - loss: 2.4798
37376/200285 [====>.........................] - ETA: 9:08 - loss: 2.4782
37504/200285 [====>.........................] - ETA: 9:08 - loss: 2.4774
37632/200285 [====>.........................] - ETA: 9:07 - loss: 2.4756
37760/200285 [====>.........................] - ETA: 9:06 - loss: 2.4750
37888/200285 [====>.........................] - ETA: 9:06 - loss: 2.4742
38016/200285 [====>.........................] - ETA: 9:06 - loss: 2.4729
38144/200285 [====>.........................] - ETA: 9:05 - loss: 2.4716
38272/200285 [====>.........................] - ETA: 9:05 - loss: 2.4710
38400/200285 [====>.........................] - ETA: 9:05 - loss: 2.4701
38528/200285 [====>.........................] - ETA: 9:05 - loss: 2.4690
38656/200285 [====>.........................] - ETA: 9:05 - loss: 2.4677
38784/200285 [====>.........................] - ETA: 9:05 - loss: 2.4669
38912/200285 [====>.........................] - ETA: 9:04 - loss: 2.4653
39040/200285 [====>.........................] - ETA: 9:04 - loss: 2.4645
39168/200285 [====>.........................] - ETA: 9:03 - loss: 2.4627
39296/200285 [====>.........................] - ETA: 9:03 - loss: 2.4619
39424/200285 [====>.........................] - ETA: 9:03 - loss: 2.4604
39552/200285 [====>.........................] - ETA: 9:02 - loss: 2.4592
39680/200285 [====>.........................] - ETA: 9:02 - loss: 2.4579
39808/200285 [====>.........................] - ETA: 9:02 - loss: 2.4576
39936/200285 [====>.........................] - ETA: 9:02 - loss: 2.4566
40064/200285 [=====>........................] - ETA: 9:01 - loss: 2.4563
40192/200285 [=====>........................] - ETA: 9:01 - loss: 2.4549
40320/200285 [=====>........................] - ETA: 9:00 - loss: 2.4535
40448/200285 [=====>........................] - ETA: 9:00 - loss: 2.4523
40576/200285 [=====>........................] - ETA: 9:00 - loss: 2.4518
*** WARNING: skipped 6880799 bytes of output ***
160256/200285 [=======================>......] - ETA: 32s - loss: 1.2854
160384/200285 [=======================>......] - ETA: 32s - loss: 1.2855
160512/200285 [=======================>......] - ETA: 31s - loss: 1.2855
160640/200285 [=======================>......] - ETA: 31s - loss: 1.2855
160768/200285 [=======================>......] - ETA: 31s - loss: 1.2855
160896/200285 [=======================>......] - ETA: 31s - loss: 1.2855
161024/200285 [=======================>......] - ETA: 31s - loss: 1.2855
161152/200285 [=======================>......] - ETA: 31s - loss: 1.2857
161280/200285 [=======================>......] - ETA: 31s - loss: 1.2857
161408/200285 [=======================>......] - ETA: 31s - loss: 1.2858
161536/200285 [=======================>......] - ETA: 31s - loss: 1.2857
161664/200285 [=======================>......] - ETA: 31s - loss: 1.2857
161792/200285 [=======================>......] - ETA: 30s - loss: 1.2857
161920/200285 [=======================>......] - ETA: 30s - loss: 1.2859
162048/200285 [=======================>......] - ETA: 30s - loss: 1.2860
162176/200285 [=======================>......] - ETA: 30s - loss: 1.2859
162304/200285 [=======================>......] - ETA: 30s - loss: 1.2859
162432/200285 [=======================>......] - ETA: 30s - loss: 1.2860
162560/200285 [=======================>......] - ETA: 30s - loss: 1.2860
162688/200285 [=======================>......] - ETA: 30s - loss: 1.2862
162816/200285 [=======================>......] - ETA: 30s - loss: 1.2861
162944/200285 [=======================>......] - ETA: 30s - loss: 1.2862
163072/200285 [=======================>......] - ETA: 29s - loss: 1.2862
163200/200285 [=======================>......] - ETA: 29s - loss: 1.2862
163328/200285 [=======================>......] - ETA: 29s - loss: 1.2860
163456/200285 [=======================>......] - ETA: 29s - loss: 1.2860
163584/200285 [=======================>......] - ETA: 29s - loss: 1.2859
163712/200285 [=======================>......] - ETA: 29s - loss: 1.2859
163840/200285 [=======================>......] - ETA: 29s - loss: 1.2859
163968/200285 [=======================>......] - ETA: 29s - loss: 1.2856
164096/200285 [=======================>......] - ETA: 29s - loss: 1.2857
164224/200285 [=======================>......] - ETA: 28s - loss: 1.2858
164352/200285 [=======================>......] - ETA: 28s - loss: 1.2858
164480/200285 [=======================>......] - ETA: 28s - loss: 1.2858
164608/200285 [=======================>......] - ETA: 28s - loss: 1.2857
164736/200285 [=======================>......] - ETA: 28s - loss: 1.2858
164864/200285 [=======================>......] - ETA: 28s - loss: 1.2858
164992/200285 [=======================>......] - ETA: 28s - loss: 1.2857
165120/200285 [=======================>......] - ETA: 28s - loss: 1.2857
165248/200285 [=======================>......] - ETA: 28s - loss: 1.2857
165376/200285 [=======================>......] - ETA: 28s - loss: 1.2859
165504/200285 [=======================>......] - ETA: 27s - loss: 1.2860
165632/200285 [=======================>......] - ETA: 27s - loss: 1.2859
165760/200285 [=======================>......] - ETA: 27s - loss: 1.2857
165888/200285 [=======================>......] - ETA: 27s - loss: 1.2858
166016/200285 [=======================>......] - ETA: 27s - loss: 1.2858
166144/200285 [=======================>......] - ETA: 27s - loss: 1.2859
166272/200285 [=======================>......] - ETA: 27s - loss: 1.2857
166400/200285 [=======================>......] - ETA: 27s - loss: 1.2858
166528/200285 [=======================>......] - ETA: 27s - loss: 1.2857
166656/200285 [=======================>......] - ETA: 27s - loss: 1.2856
166784/200285 [=======================>......] - ETA: 26s - loss: 1.2858
166912/200285 [========================>.....] - ETA: 26s - loss: 1.2858
167040/200285 [========================>.....] - ETA: 26s - loss: 1.2858
167168/200285 [========================>.....] - ETA: 26s - loss: 1.2859
167296/200285 [========================>.....] - ETA: 26s - loss: 1.2858
167424/200285 [========================>.....] - ETA: 26s - loss: 1.2859
167552/200285 [========================>.....] - ETA: 26s - loss: 1.2861
167680/200285 [========================>.....] - ETA: 26s - loss: 1.2862
167808/200285 [========================>.....] - ETA: 26s - loss: 1.2862
167936/200285 [========================>.....] - ETA: 25s - loss: 1.2863
168064/200285 [========================>.....] - ETA: 25s - loss: 1.2864
168192/200285 [========================>.....] - ETA: 25s - loss: 1.2862
168320/200285 [========================>.....] - ETA: 25s - loss: 1.2863
168448/200285 [========================>.....] - ETA: 25s - loss: 1.2862
168576/200285 [========================>.....] - ETA: 25s - loss: 1.2862
168704/200285 [========================>.....] - ETA: 25s - loss: 1.2862
168832/200285 [========================>.....] - ETA: 25s - loss: 1.2862
168960/200285 [========================>.....] - ETA: 25s - loss: 1.2861
169088/200285 [========================>.....] - ETA: 25s - loss: 1.2862
169216/200285 [========================>.....] - ETA: 24s - loss: 1.2862
169344/200285 [========================>.....] - ETA: 24s - loss: 1.2863
169472/200285 [========================>.....] - ETA: 24s - loss: 1.2862
169600/200285 [========================>.....] - ETA: 24s - loss: 1.2862
169728/200285 [========================>.....] - ETA: 24s - loss: 1.2864
169856/200285 [========================>.....] - ETA: 24s - loss: 1.2863
169984/200285 [========================>.....] - ETA: 24s - loss: 1.2864
170112/200285 [========================>.....] - ETA: 24s - loss: 1.2865
170240/200285 [========================>.....] - ETA: 24s - loss: 1.2864
170368/200285 [========================>.....] - ETA: 24s - loss: 1.2864
170496/200285 [========================>.....] - ETA: 23s - loss: 1.2865
170624/200285 [========================>.....] - ETA: 23s - loss: 1.2865
170752/200285 [========================>.....] - ETA: 23s - loss: 1.2865
170880/200285 [========================>.....] - ETA: 23s - loss: 1.2864
171008/200285 [========================>.....] - ETA: 23s - loss: 1.2866
171136/200285 [========================>.....] - ETA: 23s - loss: 1.2866
171264/200285 [========================>.....] - ETA: 23s - loss: 1.2865
171392/200285 [========================>.....] - ETA: 23s - loss: 1.2866
171520/200285 [========================>.....] - ETA: 23s - loss: 1.2867
171648/200285 [========================>.....] - ETA: 23s - loss: 1.2867
171776/200285 [========================>.....] - ETA: 22s - loss: 1.2867
171904/200285 [========================>.....] - ETA: 22s - loss: 1.2868
172032/200285 [========================>.....] - ETA: 22s - loss: 1.2869
172160/200285 [========================>.....] - ETA: 22s - loss: 1.2869
172288/200285 [========================>.....] - ETA: 22s - loss: 1.2870
172416/200285 [========================>.....] - ETA: 22s - loss: 1.2870
172544/200285 [========================>.....] - ETA: 22s - loss: 1.2870
172672/200285 [========================>.....] - ETA: 22s - loss: 1.2869
172800/200285 [========================>.....] - ETA: 22s - loss: 1.2869
172928/200285 [========================>.....] - ETA: 21s - loss: 1.2869
173056/200285 [========================>.....] - ETA: 21s - loss: 1.2870
173184/200285 [========================>.....] - ETA: 21s - loss: 1.2870
173312/200285 [========================>.....] - ETA: 21s - loss: 1.2869
173440/200285 [========================>.....] - ETA: 21s - loss: 1.2869
173568/200285 [========================>.....] - ETA: 21s - loss: 1.2869
173696/200285 [=========================>....] - ETA: 21s - loss: 1.2870
173824/200285 [=========================>....] - ETA: 21s - loss: 1.2870
173952/200285 [=========================>....] - ETA: 21s - loss: 1.2869
174080/200285 [=========================>....] - ETA: 21s - loss: 1.2871
174208/200285 [=========================>....] - ETA: 20s - loss: 1.2871
174336/200285 [=========================>....] - ETA: 20s - loss: 1.2871
174464/200285 [=========================>....] - ETA: 20s - loss: 1.2871
174592/200285 [=========================>....] - ETA: 20s - loss: 1.2870
174720/200285 [=========================>....] - ETA: 20s - loss: 1.2870
174848/200285 [=========================>....] - ETA: 20s - loss: 1.2870
174976/200285 [=========================>....] - ETA: 20s - loss: 1.2870
175104/200285 [=========================>....] - ETA: 20s - loss: 1.2870
175232/200285 [=========================>....] - ETA: 20s - loss: 1.2870
175360/200285 [=========================>....] - ETA: 20s - loss: 1.2871
175488/200285 [=========================>....] - ETA: 19s - loss: 1.2871
175616/200285 [=========================>....] - ETA: 19s - loss: 1.2871
175744/200285 [=========================>....] - ETA: 19s - loss: 1.2872
175872/200285 [=========================>....] - ETA: 19s - loss: 1.2871
176000/200285 [=========================>....] - ETA: 19s - loss: 1.2871
176128/200285 [=========================>....] - ETA: 19s - loss: 1.2870
176256/200285 [=========================>....] - ETA: 19s - loss: 1.2870
176384/200285 [=========================>....] - ETA: 19s - loss: 1.2872
176512/200285 [=========================>....] - ETA: 19s - loss: 1.2872
176640/200285 [=========================>....] - ETA: 18s - loss: 1.2872
176768/200285 [=========================>....] - ETA: 18s - loss: 1.2874
176896/200285 [=========================>....] - ETA: 18s - loss: 1.2875
177024/200285 [=========================>....] - ETA: 18s - loss: 1.2874
177152/200285 [=========================>....] - ETA: 18s - loss: 1.2873
177280/200285 [=========================>....] - ETA: 18s - loss: 1.2873
177408/200285 [=========================>....] - ETA: 18s - loss: 1.2875
177536/200285 [=========================>....] - ETA: 18s - loss: 1.2877
177664/200285 [=========================>....] - ETA: 18s - loss: 1.2875
177792/200285 [=========================>....] - ETA: 18s - loss: 1.2874
177920/200285 [=========================>....] - ETA: 17s - loss: 1.2876
178048/200285 [=========================>....] - ETA: 17s - loss: 1.2878
178176/200285 [=========================>....] - ETA: 17s - loss: 1.2879
178304/200285 [=========================>....] - ETA: 17s - loss: 1.2878
178432/200285 [=========================>....] - ETA: 17s - loss: 1.2878
178560/200285 [=========================>....] - ETA: 17s - loss: 1.2878
178688/200285 [=========================>....] - ETA: 17s - loss: 1.2880
178816/200285 [=========================>....] - ETA: 17s - loss: 1.2878
178944/200285 [=========================>....] - ETA: 17s - loss: 1.2878
179072/200285 [=========================>....] - ETA: 17s - loss: 1.2877
179200/200285 [=========================>....] - ETA: 16s - loss: 1.2875
179328/200285 [=========================>....] - ETA: 16s - loss: 1.2876
179456/200285 [=========================>....] - ETA: 16s - loss: 1.2877
179584/200285 [=========================>....] - ETA: 16s - loss: 1.2877
179712/200285 [=========================>....] - ETA: 16s - loss: 1.2877
179840/200285 [=========================>....] - ETA: 16s - loss: 1.2879
179968/200285 [=========================>....] - ETA: 16s - loss: 1.2878
180096/200285 [=========================>....] - ETA: 16s - loss: 1.2877
180224/200285 [=========================>....] - ETA: 16s - loss: 1.2876
180352/200285 [==========================>...] - ETA: 16s - loss: 1.2876
180480/200285 [==========================>...] - ETA: 15s - loss: 1.2877
180608/200285 [==========================>...] - ETA: 15s - loss: 1.2877
180736/200285 [==========================>...] - ETA: 15s - loss: 1.2878
180864/200285 [==========================>...] - ETA: 15s - loss: 1.2877
180992/200285 [==========================>...] - ETA: 15s - loss: 1.2878
181120/200285 [==========================>...] - ETA: 15s - loss: 1.2879
181248/200285 [==========================>...] - ETA: 15s - loss: 1.2878
181376/200285 [==========================>...] - ETA: 15s - loss: 1.2878
181504/200285 [==========================>...] - ETA: 15s - loss: 1.2879
181632/200285 [==========================>...] - ETA: 14s - loss: 1.2879
181760/200285 [==========================>...] - ETA: 14s - loss: 1.2880
181888/200285 [==========================>...] - ETA: 14s - loss: 1.2880
182016/200285 [==========================>...] - ETA: 14s - loss: 1.2879
182144/200285 [==========================>...] - ETA: 14s - loss: 1.2879
182272/200285 [==========================>...] - ETA: 14s - loss: 1.2879
182400/200285 [==========================>...] - ETA: 14s - loss: 1.2882
182528/200285 [==========================>...] - ETA: 14s - loss: 1.2882
182656/200285 [==========================>...] - ETA: 14s - loss: 1.2882
182784/200285 [==========================>...] - ETA: 14s - loss: 1.2883
182912/200285 [==========================>...] - ETA: 13s - loss: 1.2884
183040/200285 [==========================>...] - ETA: 13s - loss: 1.2883
183168/200285 [==========================>...] - ETA: 13s - loss: 1.2883
183296/200285 [==========================>...] - ETA: 13s - loss: 1.2882
183424/200285 [==========================>...] - ETA: 13s - loss: 1.2883
183552/200285 [==========================>...] - ETA: 13s - loss: 1.2884
183680/200285 [==========================>...] - ETA: 13s - loss: 1.2884
183808/200285 [==========================>...] - ETA: 13s - loss: 1.2884
183936/200285 [==========================>...] - ETA: 13s - loss: 1.2883
184064/200285 [==========================>...] - ETA: 13s - loss: 1.2885
184192/200285 [==========================>...] - ETA: 12s - loss: 1.2885
184320/200285 [==========================>...] - ETA: 12s - loss: 1.2885
184448/200285 [==========================>...] - ETA: 12s - loss: 1.2885
184576/200285 [==========================>...] - ETA: 12s - loss: 1.2885
184704/200285 [==========================>...] - ETA: 12s - loss: 1.2885
184832/200285 [==========================>...] - ETA: 12s - loss: 1.2885
184960/200285 [==========================>...] - ETA: 12s - loss: 1.2886
185088/200285 [==========================>...] - ETA: 12s - loss: 1.2886
185216/200285 [==========================>...] - ETA: 12s - loss: 1.2886
185344/200285 [==========================>...] - ETA: 12s - loss: 1.2885
185472/200285 [==========================>...] - ETA: 11s - loss: 1.2886
185600/200285 [==========================>...] - ETA: 11s - loss: 1.2885
185728/200285 [==========================>...] - ETA: 11s - loss: 1.2885
185856/200285 [==========================>...] - ETA: 11s - loss: 1.2885
185984/200285 [==========================>...] - ETA: 11s - loss: 1.2883
186112/200285 [==========================>...] - ETA: 11s - loss: 1.2884
186240/200285 [==========================>...] - ETA: 11s - loss: 1.2884
186368/200285 [==========================>...] - ETA: 11s - loss: 1.2884
186496/200285 [==========================>...] - ETA: 11s - loss: 1.2884
186624/200285 [==========================>...] - ETA: 10s - loss: 1.2887
186752/200285 [==========================>...] - ETA: 10s - loss: 1.2888
186880/200285 [==========================>...] - ETA: 10s - loss: 1.2888
187008/200285 [===========================>..] - ETA: 10s - loss: 1.2888
187136/200285 [===========================>..] - ETA: 10s - loss: 1.2888
187264/200285 [===========================>..] - ETA: 10s - loss: 1.2888
187392/200285 [===========================>..] - ETA: 10s - loss: 1.2889
187520/200285 [===========================>..] - ETA: 10s - loss: 1.2889
187648/200285 [===========================>..] - ETA: 10s - loss: 1.2887
187776/200285 [===========================>..] - ETA: 10s - loss: 1.2887
187904/200285 [===========================>..] - ETA: 9s - loss: 1.2887
188032/200285 [===========================>..] - ETA: 9s - loss: 1.2888
188160/200285 [===========================>..] - ETA: 9s - loss: 1.2888
188288/200285 [===========================>..] - ETA: 9s - loss: 1.2890
188416/200285 [===========================>..] - ETA: 9s - loss: 1.2891
188544/200285 [===========================>..] - ETA: 9s - loss: 1.2889
188672/200285 [===========================>..] - ETA: 9s - loss: 1.2889
188800/200285 [===========================>..] - ETA: 9s - loss: 1.2888
188928/200285 [===========================>..] - ETA: 9s - loss: 1.2887
189056/200285 [===========================>..] - ETA: 9s - loss: 1.2886
189184/200285 [===========================>..] - ETA: 8s - loss: 1.2886
189312/200285 [===========================>..] - ETA: 8s - loss: 1.2886
189440/200285 [===========================>..] - ETA: 8s - loss: 1.2886
189568/200285 [===========================>..] - ETA: 8s - loss: 1.2886
189696/200285 [===========================>..] - ETA: 8s - loss: 1.2885
189824/200285 [===========================>..] - ETA: 8s - loss: 1.2885
189952/200285 [===========================>..] - ETA: 8s - loss: 1.2884
190080/200285 [===========================>..] - ETA: 8s - loss: 1.2883
190208/200285 [===========================>..] - ETA: 8s - loss: 1.2881
190336/200285 [===========================>..] - ETA: 7s - loss: 1.2881
190464/200285 [===========================>..] - ETA: 7s - loss: 1.2882
190592/200285 [===========================>..] - ETA: 7s - loss: 1.2882
190720/200285 [===========================>..] - ETA: 7s - loss: 1.2882
190848/200285 [===========================>..] - ETA: 7s - loss: 1.2881
190976/200285 [===========================>..] - ETA: 7s - loss: 1.2881
191104/200285 [===========================>..] - ETA: 7s - loss: 1.2882
191232/200285 [===========================>..] - ETA: 7s - loss: 1.2881
191360/200285 [===========================>..] - ETA: 7s - loss: 1.2881
191488/200285 [===========================>..] - ETA: 7s - loss: 1.2881
191616/200285 [===========================>..] - ETA: 6s - loss: 1.2880
191744/200285 [===========================>..] - ETA: 6s - loss: 1.2880
191872/200285 [===========================>..] - ETA: 6s - loss: 1.2879
192000/200285 [===========================>..] - ETA: 6s - loss: 1.2880
192128/200285 [===========================>..] - ETA: 6s - loss: 1.2880
192256/200285 [===========================>..] - ETA: 6s - loss: 1.2879
192384/200285 [===========================>..] - ETA: 6s - loss: 1.2880
192512/200285 [===========================>..] - ETA: 6s - loss: 1.2880
192640/200285 [===========================>..] - ETA: 6s - loss: 1.2880
192768/200285 [===========================>..] - ETA: 6s - loss: 1.2880
192896/200285 [===========================>..] - ETA: 5s - loss: 1.2881
193024/200285 [===========================>..] - ETA: 5s - loss: 1.2883
193152/200285 [===========================>..] - ETA: 5s - loss: 1.2884
193280/200285 [===========================>..] - ETA: 5s - loss: 1.2886
193408/200285 [===========================>..] - ETA: 5s - loss: 1.2886
193536/200285 [===========================>..] - ETA: 5s - loss: 1.2887
193664/200285 [============================>.] - ETA: 5s - loss: 1.2891
193792/200285 [============================>.] - ETA: 5s - loss: 1.2890
193920/200285 [============================>.] - ETA: 5s - loss: 1.2890
194048/200285 [============================>.] - ETA: 5s - loss: 1.2890
194176/200285 [============================>.] - ETA: 4s - loss: 1.2889
194304/200285 [============================>.] - ETA: 4s - loss: 1.2889
194432/200285 [============================>.] - ETA: 4s - loss: 1.2888
194560/200285 [============================>.] - ETA: 4s - loss: 1.2888
194688/200285 [============================>.] - ETA: 4s - loss: 1.2888
194816/200285 [============================>.] - ETA: 4s - loss: 1.2887
194944/200285 [============================>.] - ETA: 4s - loss: 1.2886
195072/200285 [============================>.] - ETA: 4s - loss: 1.2887
195200/200285 [============================>.] - ETA: 4s - loss: 1.2888
195328/200285 [============================>.] - ETA: 3s - loss: 1.2888
195456/200285 [============================>.] - ETA: 3s - loss: 1.2889
195584/200285 [============================>.] - ETA: 3s - loss: 1.2890
195712/200285 [============================>.] - ETA: 3s - loss: 1.2890
195840/200285 [============================>.] - ETA: 3s - loss: 1.2890
195968/200285 [============================>.] - ETA: 3s - loss: 1.2891
196096/200285 [============================>.] - ETA: 3s - loss: 1.2891
196224/200285 [============================>.] - ETA: 3s - loss: 1.2891
196352/200285 [============================>.] - ETA: 3s - loss: 1.2893
196480/200285 [============================>.] - ETA: 3s - loss: 1.2893
196608/200285 [============================>.] - ETA: 2s - loss: 1.2892
196736/200285 [============================>.] - ETA: 2s - loss: 1.2891
196864/200285 [============================>.] - ETA: 2s - loss: 1.2893
196992/200285 [============================>.] - ETA: 2s - loss: 1.2891
197120/200285 [============================>.] - ETA: 2s - loss: 1.2892
197248/200285 [============================>.] - ETA: 2s - loss: 1.2892
197376/200285 [============================>.] - ETA: 2s - loss: 1.2891
197504/200285 [============================>.] - ETA: 2s - loss: 1.2891
197632/200285 [============================>.] - ETA: 2s - loss: 1.2892
197760/200285 [============================>.] - ETA: 2s - loss: 1.2892
197888/200285 [============================>.] - ETA: 1s - loss: 1.2892
198016/200285 [============================>.] - ETA: 1s - loss: 1.2893
198144/200285 [============================>.] - ETA: 1s - loss: 1.2894
198272/200285 [============================>.] - ETA: 1s - loss: 1.2893
198400/200285 [============================>.] - ETA: 1s - loss: 1.2893
198528/200285 [============================>.] - ETA: 1s - loss: 1.2893
198656/200285 [============================>.] - ETA: 1s - loss: 1.2894
198784/200285 [============================>.] - ETA: 1s - loss: 1.2897
198912/200285 [============================>.] - ETA: 1s - loss: 1.2897
199040/200285 [============================>.] - ETA: 1s - loss: 1.2897
199168/200285 [============================>.] - ETA: 0s - loss: 1.2897
199296/200285 [============================>.] - ETA: 0s - loss: 1.2899
199424/200285 [============================>.] - ETA: 0s - loss: 1.2900
199552/200285 [============================>.] - ETA: 0s - loss: 1.2900
199680/200285 [============================>.] - ETA: 0s - loss: 1.2900
199808/200285 [============================>.] - ETA: 0s - loss: 1.2899
199936/200285 [============================>.] - ETA: 0s - loss: 1.2900
200064/200285 [============================>.] - ETA: 0s - loss: 1.2902
200192/200285 [============================>.] - ETA: 0s - loss: 1.2900
200285/200285 [==============================] - 161s 804us/step - loss: 1.2899
----- diversity: 0.2
----- Generating with seed: "re fostered; the species needs itself as"
re fostered; the species needs itself as a man is a strong for the strength of the subjection of the strength of the still finally and all that is a present and the strength of the power of the strive of the sense of the probably and the state of the subjection of the spiritual and stands and the strength of the strength of the subjection of the strange, and all that is the strong stands to the former and the strength of the strength of
----- diversity: 0.5
----- Generating with seed: "re fostered; the species needs itself as"
re fostered; the species needs itself as a delight of god, the far to mankind responsibility, and all the head
and the problem
of the same type--that is the content, to us. the instinct it is sociatisment and serrection of a present and repultion of the will and delight and complancess of the strong
that is the secret and ancient devours, a strong strength and habits of the science and and laten his state to the concerned to the stread
----- diversity: 1.0
----- Generating with seed: "re fostered; the species needs itself as"
re fostered; the species needs itself as' by a child.
1
9r
=whet for from a altrre as well conscience that there are that is always bemn) pernewlies, and that sthe or unines"--but in his consciven to us? but as attaine and internil, exception id strength of frenchmen spects.--the most bodyy and came to a nemensy in the glooly, reun in every metaphorion; or as srigor appreciates, have path plant, the bestow daesersy; this,--according to
----- diversity: 1.2
----- Generating with seed: "re fostered; the species needs itself as"
re fostered; the species needs itself as
side, such belief.
25xaxence; the most fical tumm his not glan apttignd burding, the longly?incitians,
toripaped seems ones"--a natural libering,
free fortune, suskinatic wisre possessing couragematation, exulation: with a long especient,
and they which has been regear who have physeem being i him iting
were-do againstives a cases of a cries:
"his fact
agr ity gup.
6hxthsb these, io do alvated
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Generative Networks
Concept:
If a set of network weights can convert an image of the numeral 8 or a cat
into the classification "8" or "cat" ...
Does it contain enough information to do the reverse?
I.e., can we ask a network what "8" looks like and get a picture?
Let's think about this for a second. Clearly the classifications have far fewer bits of entropy than the source images' theoretical limit.
- Cat (in cat-vs-dog) has just 1 bit, where perhaps a 256x256 grayscale image has up to 512k bits.
- 8 (in MNIST) has \({log _2 10}\) or a little over 3 bits, where a 28x28 grayscale image has over 6000 bits.
So at first, this would seem difficult or impossible.
But ... let's do a thought experiment.
- Children can do this easily
- We could create a lookup table of, say, digit -> image trivially, and use that as a first approximation
Those approaches seem like cheating. But let's think about how they work.
If a child (or adult) draws a cat (or number 8), they are probably not drawing any specific cat (or 8). They are drawing a general approximation of a cat based on
- All of the cats they've seen
- What they remember as the key elements of a cat (4 legs, tail, pointy ears)
- A lookup table substitutes one specific cat or 8 ... and, especially in the case of the 8, that may be fine. The only thing we "lose" is the diversity of things that all mapped to cat (or 8) -- and discarding that information was exactly our goal when building a classifier
The "8" is even simpler: we learn that a number is an idea, not a specific instance, so anything that another human recognizes as 8 is good enough. We are not even trying to make a particular shape, just one that represents our encoded information that distinguishes 8 from other possible symbols in the context and the eye of the viewer.
This should remind you a bit of the KL Divergence we talked about at the start: we are providing just enough information (entropy or surprise) to distinguish the cat or "8" from the other items that a human receiver might be expecting to see.
And where do our handwritten "pixels" come from? No image in particular -- they are totally synthetic based on a probability distribution.
These considerations make it sound more likely that a computer could perform the same task.
But what would the weights really represent? what could they generate?
The weights we learn in classification represent the distinguishing features of a class, across all training examples of the class, modified to overlap minimally with features of other classes. KL divergence again.
To be concrete, if we trained a model on just a few dozen MNIST images using pixels, it would probably learn the 3 or 4 "magic" pixels that happened to distinguish the 8s in that dataset. Trying to generate from that information would yield strong confidence about those magic pixels, but would look like dots to us humans.
On the other hand, if we trained on a very large number of MNIST images -- say we use the convnet this time -- the model's weights should represent general filters of masks for features that distinguish an 8. And if we try to reverse the process by amplifying just those filters, we should get a blurry statistical distribution of those very features. The approximate shape of the Platonic "8"!
Mechanically, How Could This Work?
Let's start with a simpler model called an auto-encoder.
An autoencoder's job is to take a large representation of a record and find weights that represent that record in a smaller encoding, subject to the constraint that the decoded version should match the original as closely as possible.
A bit like training a JPEG encoder to compress images by scoring it with the loss between the original image and the decompressed version of the lossy compressed image.

One nice aspect of this is that it is unsupervised -- i.e., we do not need any ground-truth or human-generated labels in order to find the error and train. The error is always the difference between the output and the input, and the goal is to minimize this over many examples, thus minimize in the general case.
We can do this with a simple multilayer perceptron network. Or, we can get fancier and do this with a convolutional network. In reverse, the convolution (typically called "transposed convolution" or "deconvolution") is an upsampling operation across space (in images) or space & time (in audio/video).
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import to_categorical
import sklearn.datasets
import datetime
import matplotlib.pyplot as plt
import numpy as np
train_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-train.txt"
test_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-test.txt"
X_train, y_train = sklearn.datasets.load_svmlight_file(train_libsvm, n_features=784)
X_train = X_train.toarray()
X_test, y_test = sklearn.datasets.load_svmlight_file(test_libsvm, n_features=784)
X_test = X_test.toarray()
model = Sequential()
model.add(Dense(30, input_dim=784, kernel_initializer='normal', activation='relu'))
model.add(Dense(784, kernel_initializer='normal', activation='relu'))
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mean_squared_error', 'binary_crossentropy'])
start = datetime.datetime.today()
history = model.fit(X_train, X_train, epochs=5, batch_size=100, validation_split=0.1, verbose=2)
scores = model.evaluate(X_test, X_test)
print
for i in range(len(model.metrics_names)):
print("%s: %f" % (model.metrics_names[i], scores[i]))
print ("Start: " + str(start))
end = datetime.datetime.today()
print ("End: " + str(end))
print ("Elapse: " + str(end-start))
fig, ax = plt.subplots()
fig.set_size_inches((4,4))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
display(fig)
ax.clear()
fig.set_size_inches((5,5))
ax.imshow(np.reshape(X_test[61], (28,28)), cmap='gray')
display(fig)
encode_decode = model.predict(np.reshape(X_test[61], (1, 784)))
ax.clear()
ax.imshow(np.reshape(encode_decode, (28,28)), cmap='gray')
display(fig)
Any ideas about those black dots in the upper right?
Pretty cool. So we're all done now, right? Now quite...
The problem with the autoencoder is it's "too good" at its task.
It is optimized to compress exactly the input record set, so it is trained only to create records it has seen. If the middle layer, or information bottleneck, is tight enough, the coded records use all of the information space in the middle layer.
So any value in the middle layer decodes to exactly one already-seen exemplar.
In our example, and most autoencoders, there is more space in the middle layer but the coded values are not distributed in any sensible way. So we can decode a random vector and we'll probably just get garbage.
v = np.random.randn(30)
v = np.array(np.reshape(v, (1, 30)))
import tensorflow as tf
t = tf.convert_to_tensor(v, dtype='float32')
out = model.layers[1](t)
from keras import backend as K
with K.get_session().as_default():
output = out.eval()
ax.clear()
ax.imshow(np.reshape(output, (28,28)), cmap='gray')
display(fig)
The Goal is to Generate a Variety of New Output From a Variety of New Inputs
... Where the Class/Category is Common (i.e., all 8s or Cats)
Some considerations:
- Is "generative content" something new? Or something true?
- In a Platonic sense, maybe, but in reality it's literally a probabilistic guess based on the training data!
- E.g., law enforcement photo enhancment
- How do we train?
- If we score directly against the training data (like in the autoencoder), the network will be very conservative, generating only examples that it has seen.
- In extreme cases, it will always generate a single (or small number) of examples, since those score well. This is known as mode collapse, since the network learns to locate the modes in the input distribution.
Two principal approaches / architectures (2015-)
Generative Adversarial Networks (GAN) and Variational Autoencoders (VAE)
Variational Autoencoder (VAE)
Our autoencoder was able to generate images, but the problem was that arbitrary input vectors don't map to anything meaningful. As discussed, this is partly by design -- the training of the VAE is for effectively for compressing a specific input dataset.
What we would like, is that if we start with a valid input vector and move a bit on some direction, we get a plausible output that is also changed in some way.
ASIDE: Manifold Hypothesis
The manifold hypothesis is that the interesting, relevant, or critical subspaces in the space of all vector inputs are actually low(er) dimensional manifolds. A manifold is a space where each point has a neighborhood that behaves like (is homeomorphic to) \({\Bbb R^n}\). So we would like to be able to move a small amount and have only a small amount of change, not a sudden discontinuous change.
The key feature of Variational Autoencoders is that we add a constraint on the encoded representation of our data: namely, that it follows a Gaussian distribution. Since the Gaussian is determined by its mean and variance (or standard deviation), we can model it as a k-variate Gaussian with these two parameters (\({\mu}\) and \({\sigma}\)) for each value of k.


One challenge is how to balance accurate reproduction of the input (traditional autoencoder loss) with the requirement that we match a Gaussian distribution. We can force the network to optimize both of these goals by creating a custom error function that sums up two components:
- How well we match the input, calculated as binary crossentropy or MSE loss
- How well we match a Gaussian, calculated as KL divergence from the Gaussian distribution
We can easily implement a custom loss function and pass it as a parameter to the optimizer in Keras.
The Keras source examples folder contains an elegant simple implementation, which we'll discuss below. It's a little more complex than the code we've seen so far, but we'll clarify the innovations:
- Custom loss functions that combined KL divergence and cross-entropy loss
- Custom "Lambda" layer that provides the sampling from the encoded distribution
Overall it's probably simpler than you might expect. Let's start it (since it takes a few minutes to train) and discuss the code:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from keras.layers import Input, Dense, Lambda
from keras.models import Model
from keras import backend as K
from keras import objectives
from keras.datasets import mnist
import sklearn.datasets
batch_size = 100
original_dim = 784
latent_dim = 2
intermediate_dim = 256
nb_epoch = 50
epsilon_std = 1.0
x = Input(batch_shape=(batch_size, original_dim))
h = Dense(intermediate_dim, activation='relu')(x)
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.,
stddev=epsilon_std)
return z_mean + K.exp(z_log_var / 2) * epsilon
# note that "output_shape" isn't necessary with the TensorFlow backend
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
# we instantiate these layers separately so as to reuse them later
decoder_h = Dense(intermediate_dim, activation='relu')
decoder_mean = Dense(original_dim, activation='sigmoid')
h_decoded = decoder_h(z)
x_decoded_mean = decoder_mean(h_decoded)
def vae_loss(x, x_decoded_mean):
xent_loss = original_dim * objectives.binary_crossentropy(x, x_decoded_mean)
kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
return xent_loss + kl_loss
vae = Model(x, x_decoded_mean)
vae.compile(optimizer='rmsprop', loss=vae_loss)
train_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-train.txt"
test_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-test.txt"
x_train, y_train = sklearn.datasets.load_svmlight_file(train_libsvm, n_features=784)
x_train = x_train.toarray()
x_test, y_test = sklearn.datasets.load_svmlight_file(test_libsvm, n_features=784)
x_test = x_test.toarray()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
vae.fit(x_train, x_train,
shuffle=True,
epochs=nb_epoch,
batch_size=batch_size,
validation_data=(x_test, x_test), verbose=2)
# build a model to project inputs on the latent space
encoder = Model(x, z_mean)
Train on 60000 samples, validate on 10000 samples
Epoch 1/50
- 28s - loss: 191.3552 - val_loss: 174.0489
Epoch 2/50
- 22s - loss: 170.7199 - val_loss: 168.6271
Epoch 3/50
- 22s - loss: 167.0845 - val_loss: 165.6178
Epoch 4/50
- 24s - loss: 164.9294 - val_loss: 164.0987
Epoch 5/50
- 23s - loss: 163.3526 - val_loss: 162.8324
Epoch 6/50
- 24s - loss: 162.1426 - val_loss: 161.6388
Epoch 7/50
- 24s - loss: 161.0804 - val_loss: 161.0039
Epoch 8/50
- 24s - loss: 160.1358 - val_loss: 160.0695
Epoch 9/50
- 24s - loss: 159.2005 - val_loss: 158.9536
Epoch 10/50
- 24s - loss: 158.4628 - val_loss: 158.3245
Epoch 11/50
- 24s - loss: 157.7760 - val_loss: 158.3026
Epoch 12/50
- 23s - loss: 157.1977 - val_loss: 157.5024
Epoch 13/50
- 23s - loss: 156.6953 - val_loss: 157.1289
Epoch 14/50
- 22s - loss: 156.2697 - val_loss: 156.8286
Epoch 15/50
- 24s - loss: 155.8225 - val_loss: 156.1923
Epoch 16/50
- 24s - loss: 155.5014 - val_loss: 156.2340
Epoch 17/50
- 21s - loss: 155.1700 - val_loss: 155.6375
Epoch 18/50
- 21s - loss: 154.8542 - val_loss: 155.6273
Epoch 19/50
- 20s - loss: 154.5926 - val_loss: 155.3817
Epoch 20/50
- 20s - loss: 154.3028 - val_loss: 154.9080
Epoch 21/50
- 20s - loss: 154.0440 - val_loss: 155.1275
Epoch 22/50
- 21s - loss: 153.8262 - val_loss: 154.7661
Epoch 23/50
- 21s - loss: 153.5559 - val_loss: 155.0041
Epoch 24/50
- 21s - loss: 153.3750 - val_loss: 154.7824
Epoch 25/50
- 21s - loss: 153.1672 - val_loss: 154.0173
Epoch 26/50
- 21s - loss: 152.9496 - val_loss: 154.1547
Epoch 27/50
- 21s - loss: 152.7783 - val_loss: 153.7538
Epoch 28/50
- 20s - loss: 152.6183 - val_loss: 154.2638
Epoch 29/50
- 20s - loss: 152.3948 - val_loss: 153.4925
Epoch 30/50
- 22s - loss: 152.2362 - val_loss: 153.3316
Epoch 31/50
- 21s - loss: 152.1005 - val_loss: 153.6578
Epoch 32/50
- 20s - loss: 151.9579 - val_loss: 153.3381
Epoch 33/50
- 19s - loss: 151.8026 - val_loss: 153.2551
Epoch 34/50
- 21s - loss: 151.6616 - val_loss: 153.2799
Epoch 35/50
- 21s - loss: 151.5314 - val_loss: 153.5594
Epoch 36/50
- 21s - loss: 151.4036 - val_loss: 153.2309
Epoch 37/50
- 21s - loss: 151.2607 - val_loss: 152.8981
Epoch 38/50
- 20s - loss: 151.1211 - val_loss: 152.9517
Epoch 39/50
- 21s - loss: 151.0164 - val_loss: 152.6791
Epoch 40/50
- 22s - loss: 150.8922 - val_loss: 152.5144
Epoch 41/50
- 21s - loss: 150.8052 - val_loss: 152.3929
Epoch 42/50
- 21s - loss: 150.6794 - val_loss: 152.6652
Epoch 43/50
- 20s - loss: 150.5621 - val_loss: 152.5482
Epoch 44/50
- 21s - loss: 150.4409 - val_loss: 152.0705
Epoch 45/50
- 22s - loss: 150.3552 - val_loss: 152.2069
Epoch 46/50
- 21s - loss: 150.2257 - val_loss: 152.0479
Epoch 47/50
- 21s - loss: 150.1526 - val_loss: 152.4409
Epoch 48/50
- 22s - loss: 150.0543 - val_loss: 152.1632
Epoch 49/50
- 21s - loss: 149.9764 - val_loss: 152.0441
Epoch 50/50
- 21s - loss: 149.8765 - val_loss: 151.8960
# display a 2D plot of the digit classes in the latent space
x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
fig, ax = plt.subplots()
fig.set_size_inches((8,7))
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
display(fig)
# build a digit generator that can sample from the learned distribution
decoder_input = Input(shape=(latent_dim,))
_h_decoded = decoder_h(decoder_input)
_x_decoded_mean = decoder_mean(_h_decoded)
generator = Model(decoder_input, _x_decoded_mean)
# display a 2D manifold of the digits
n = 15 # figure with 15x15 digits
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
# linearly spaced coordinates on the unit square were transformed through the inverse CDF (ppf) of the Gaussian
# to produce values of the latent variables z, since the prior of the latent space is Gaussian
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z_sample = np.array([[xi, yi]])
x_decoded = generator.predict(z_sample)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit
fig, ax = plt.subplots()
fig.set_size_inches((7,7))
ax.imshow(figure, cmap='Greys_r')
display(fig)
Note that it is blurry, and "manipulable" by moving through the latent space!
It is not intuitively obvious where the calculation of the KL divergence comes from, and in general there is not a simple analytic way to derive KL divergence for arbitrary distributions. Because we have assumptions about Gaussians here, this is a special case -- the derivation is included in the Auto-Encoding Variational Bayes paper (2014; https://arxiv.org/pdf/1312.6114.pdf)
Generative Adversarial Network (GAN)
The GAN, popularized recently by Ian Goodfellow's work, consists of two networks:
- Generator network (that initially generates output from noise)
- Discriminator network (trained with real data, to simply distinguish 2 class: real and fake)
- The discriminator is also sometimes called the "A" or adversarial network
The basic procedure for building a GAN is to train both neworks in tandem according to the following simple procedure:
- Generate bogus output from "G"
- Train "D" with real and bogus data, labeled properly
- Train "G" to target the "real/true/1" label by
- taking the "stacked" G + D model
- feeding noise in at the start (G) end
- and backpropagating from the real/true/1 distribution at the output (D) end
As always, there are lots of variants! But this is the core idea, as illustrated in the following code.
Zackory Erickson's example is so elegant and clear, I've used included it from https://github.com/Zackory/Keras-MNIST-GAN
Once again, we'll start it running first, since it takes a while to train.
import os
import numpy as np
import matplotlib.pyplot as plt
from keras.layers import Input
from keras.models import Model, Sequential
from keras.layers.core import Reshape, Dense, Dropout, Flatten
from keras.layers.advanced_activations import LeakyReLU
from keras.layers.convolutional import Convolution2D, UpSampling2D
from keras.layers.normalization import BatchNormalization
from keras.regularizers import l1, l1_l2
from keras.optimizers import Adam
from keras import backend as K
from keras import initializers
import sklearn.datasets
K.set_image_data_format('channels_last')
# Deterministic output.
# Tired of seeing the same results every time? Remove the line below.
np.random.seed(1000)
# The results are a little better when the dimensionality of the random vector is only 10.
# The dimensionality has been left at 100 for consistency with other GAN implementations.
randomDim = 100
train_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-train.txt"
test_libsvm = "/dbfs/databricks-datasets/mnist-digits/data-001/mnist-digits-test.txt"
X_train, y_train = sklearn.datasets.load_svmlight_file(train_libsvm, n_features=784)
X_train = X_train.toarray()
X_test, y_test = sklearn.datasets.load_svmlight_file(test_libsvm, n_features=784)
X_test = X_test.toarray()
X_train = (X_train.astype(np.float32) - 127.5)/127.5
X_train = X_train.reshape(60000, 784)
# Function for initializing network weights
def initNormal():
return initializers.normal(stddev=0.02)
# Optimizer
adam = Adam(lr=0.0002, beta_1=0.5)
generator = Sequential()
generator.add(Dense(256, input_dim=randomDim, kernel_initializer=initializers.normal(stddev=0.02)))
generator.add(LeakyReLU(0.2))
generator.add(Dense(512))
generator.add(LeakyReLU(0.2))
generator.add(Dense(1024))
generator.add(LeakyReLU(0.2))
generator.add(Dense(784, activation='tanh'))
generator.compile(loss='binary_crossentropy', optimizer=adam)
discriminator = Sequential()
discriminator.add(Dense(1024, input_dim=784, kernel_initializer=initializers.normal(stddev=0.02)))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(rate = 1-0.3)) #new parameter rate instead of keep_prob (rate = 1-keep_prob)
discriminator.add(Dense(512))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(rate = 1-0.3)) #new parameter rate instead of keep_prob (rate = 1-keep_prob)
discriminator.add(Dense(256))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(rate = 1-0.3)) #new parameter rate instead of keep_prob (rate = 1-keep_prob)
discriminator.add(Dense(1, activation='sigmoid'))
discriminator.compile(loss='binary_crossentropy', optimizer=adam)
# Combined network
discriminator.trainable = False
ganInput = Input(shape=(randomDim,))
x = generator(ganInput)
ganOutput = discriminator(x)
gan = Model(inputs=ganInput, outputs=ganOutput)
gan.compile(loss='binary_crossentropy', optimizer=adam)
dLosses = []
gLosses = []
# Plot the loss from each batch
def plotLoss(epoch):
plt.figure(figsize=(10, 8))
plt.plot(dLosses, label='Discriminitive loss')
plt.plot(gLosses, label='Generative loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.savefig('/dbfs/FileStore/gan_loss_epoch_%d.png' % epoch)
# Create a wall of generated MNIST images
def plotGeneratedImages(epoch, examples=100, dim=(10, 10), figsize=(10, 10)):
noise = np.random.normal(0, 1, size=[examples, randomDim])
generatedImages = generator.predict(noise)
generatedImages = generatedImages.reshape(examples, 28, 28)
plt.figure(figsize=figsize)
for i in range(generatedImages.shape[0]):
plt.subplot(dim[0], dim[1], i+1)
plt.imshow(generatedImages[i], interpolation='nearest', cmap='gray_r')
plt.axis('off')
plt.tight_layout()
plt.savefig('/dbfs/FileStore/gan_generated_image_epoch_%d.png' % epoch)
# Save the generator and discriminator networks (and weights) for later use
def saveModels(epoch):
generator.save('/tmp/gan_generator_epoch_%d.h5' % epoch)
discriminator.save('/tmp/gan_discriminator_epoch_%d.h5' % epoch)
def train(epochs=1, batchSize=128):
batchCount = X_train.shape[0] // batchSize
print('Epochs:', epochs)
print('Batch size:', batchSize)
print('Batches per epoch:', batchCount)
for e in range(1, epochs+1):
print('-'*15, 'Epoch %d' % e, '-'*15)
for _ in range(batchCount):
# Get a random set of input noise and images
noise = np.random.normal(0, 1, size=[batchSize, randomDim])
imageBatch = X_train[np.random.randint(0, X_train.shape[0], size=batchSize)]
# Generate fake MNIST images
generatedImages = generator.predict(noise)
# print np.shape(imageBatch), np.shape(generatedImages)
X = np.concatenate([imageBatch, generatedImages])
# Labels for generated and real data
yDis = np.zeros(2*batchSize)
# One-sided label smoothing
yDis[:batchSize] = 0.9
# Train discriminator
discriminator.trainable = True
dloss = discriminator.train_on_batch(X, yDis)
# Train generator
noise = np.random.normal(0, 1, size=[batchSize, randomDim])
yGen = np.ones(batchSize)
discriminator.trainable = False
gloss = gan.train_on_batch(noise, yGen)
# Store loss of most recent batch from this epoch
dLosses.append(dloss)
gLosses.append(gloss)
if e == 1 or e % 10 == 0:
plotGeneratedImages(e)
saveModels(e)
# Plot losses from every epoch
plotLoss(e)
train(10, 128)
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:3733: calling dropout (from tensorflow.python.ops.nn_ops) with keep_prob is deprecated and will be removed in a future version.
Instructions for updating:
Please use `rate` instead of `keep_prob`. Rate should be set to `rate = 1 - keep_prob`.
Epochs: 10
Batch size: 128
Batches per epoch: 468
--------------- Epoch 1 ---------------
--------------- Epoch 2 ---------------
--------------- Epoch 3 ---------------
--------------- Epoch 4 ---------------
--------------- Epoch 5 ---------------
--------------- Epoch 6 ---------------
--------------- Epoch 7 ---------------
--------------- Epoch 8 ---------------
--------------- Epoch 9 ---------------
--------------- Epoch 10 ---------------
Which Strategy to Use?
This is definitely an area of active research, so you'll want to experiment with both of these approaches.
GANs typically produce "sharper pictures" -- the adversarial loss is better than the combined MSE/XE + KL loss used in VAEs, but then again, that's partly by design.
VAEs are -- as seen above -- blurrier but more manipulable. One way of thinking about the multivariate Gaussian representation is that VAEs are trained to find some "meaning" in variation along each dimensin. And, in fact, with specific training it is possible to get them to associate specific meanings like color, translation, rotation, etc. to those dimensions.
Where Next?
Keep an eye on Medium articles and others at sites like towardsdatascience:
Here is one which caught my eve in 2019:
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Playing Games and Driving Cars: Reinforcement Learning

In a Nutshell
In reinforcement learning, an agent takes multiple actions, and the positive or negative outcome of those actions serves as a loss function for subsequent training.
Training an Agent
What is an agent?
How is training an agent different from training the models we've used so far?
Most things stay the same, and we can use all of the knowledge we've built:
- We can use any or all of the network models, including feed-forward, convolutional, recurrent, and combinations of those.
- We will still train in batches using some variant of gradient descent
- As before, the model will ideally learn a complex non-obvious function of many parameters
A few things change ... well, not really change, but "specialize":
- The inputs may start out as entire frames (or frame deltas) of a video feed
- We may feature engineer more explicitly (or not)
- The ouputs may be a low-cardinality set of categories that represent actions (e.g., direction of a digital joystick, or input to a small number of control systems)
- We may model state explicitly (outside the network) as well as implicitly (inside the network)
- The function we're learning is one which will "tell our agent what to do" or -- assuming there is no disconnect between knowing what to do and doing it, the function will essentially be the agent
- The loss function depends on the outcome of the game, and the game requires many actions to reach an outcome, and so requires some slightly different approaches from the ones we've used before.
Principal Approaches: Deep Q-Learning and Policy Gradient Learning
-
Policy Gradient is straightforward and shows a lot of research promise, but can be quite difficult to use. The challenge is less in the math, code, or concepts, and more in terms of effective training. We'll look very briefly at PG.
-
Deep Q-Learning is more constrained and a little more complex mathematically. These factors would seem to cut against the use of DQL, but they allow for relatively fast and effective training, so they are very widely used. We'll go deeper into DQL and work with an example.
There are, of course, many variants on these as well as some other strategies.
Policy Gradient Learning
With Policy Gradient Learning, we directly try to learn a "policy" function that selects a (possibly continuous-valued) move for an agent to make given the current state of the "world."
We want to maximize total discounted future reward, but we do not need discrete actions to take or a model that tells us a specific "next reward."
Instead, we can make fine-grained moves and we can collect all the moves that lead to a reward, and then apply that reward to all of them.
ASIDE: The term gradient here comes from a formula which indicates the gradient (or steepest direction) to improve the policy parameters with respect to the loss function. That is, which direction to adjust the parameters to maximize improvement in expected total reward.
In some sense, this is a more straightforward, direct approach than the other approach we'll work with, Deep Q-Learning.
Challenges with Policy Gradients
Policy gradients, despite achieving remarkable results, are a form of brute-force solution.
Thus they require a large amount of input data and extraordinary amounts of training time.
Some of these challenges come down to the credit assignment problem -- properly attributing reward to actions in the past which may (or may not) be responsible for the reward -- and thus some mitigations include more complex reward functions, adding more frequent reward training into the system, and adding domain knowledge to the policy, or adding an entire separate network, called a "critic network" to learn to provide feedback to the actor network.
Another challenge is the size of the search space, and tractable approaches to exploring it.
PG is challenging to use in practice, though there are a number of "tricks" in various publications that you can try.
Next Steps
-
Great post by Andrej Karpathy on policy gradient learning: http://karpathy.github.io/2016/05/31/rl/
-
A nice first step on policy gradients with real code: Using Keras and Deep Deterministic Policy Gradient to play TORCS: https://yanpanlau.github.io/2016/10/11/Torcs-Keras.html
If you'd like to explore a variety of reinforcement learning techniques, Mattias Lappert at the Karlsruhe Institute of Technology, has created an add-on framework for Keras that implements a variety of state-of-the-art RL techniques, including discussed today.
His framework, KerasRL is at https://github.com/matthiasplappert/keras-rl and includes examples that integrate with OpenAI gym.
Deep Q-Learning
Deep Q-Learning is deep learning applied to "Q-Learning."
So what is Q-Learning?
Q-Learning is a model that posits a map for optimal actions for each possible state in a game.
Specifically, given a state and an action, there is a "Q-function" that provides the value or quality (the Q stands for quality) of that action taken in that state.
So, if an agent is in state s, choosing an action could be as simple as looking at Q(s, a) for all a, and choosing the highest "quality value" -- aka 
There are some other considerations, such as explore-exploit tradeoff, but let's focus on this Q function.
In small state spaces, this function can be represented as a table, a bit like basic strategy blackjack tables.

Even a simple Atari-style video game may have hundreds of thousands of states, though. This is where the neural network comes in.
What we need is a way to learn a Q function, when we don't know what the error of a particular move is, since the error (loss) may be dependent on many future actions and can also be non-deterministic (e.g., if there are randomly generated enemies or conditions in the game).
The tricks -- or insights -- here are:
[1] Model the total future reward -- what we're really after -- as a recursive calculation from the immediate reward (r) and future outcomes:

- \({\gamma}\) is a "discount factor" on future reward
- Assume the game terminates or "effectively terminates" to make the recursion tractable
- This equation is a simplified case of the Bellman Equation
[2] Assume that if you iteratively run this process starting with an arbitrary Q model, and you train the Q model with actual outcomes, your Q model will eventually converge toward the "true" Q function * This seems intuitively to resemble various Monte Carlo sampling methods (if that helps at all)
As improbable as this might seem at first for teaching an agent a complex game or task, it actually works, and in a straightforward way.
How do we apply this to our neural network code?
Unlike before, when we called "fit" to train a network automatically, here we'll need some interplay between the agent's behavior in the game and the training. That is, we need the agent to play some moves in order to get actual numbers to train with. And as soon as we have some actual numbers, we want to do a little training with them right away so that our Q function improves. So we'll alternate one or more in-game actions with a manual call to train on a single batch of data.
The algorithm looks like this (credit for the nice summary to Tambet Matiisen; read his longer explanation at https://neuro.cs.ut.ee/demystifying-deep-reinforcement-learning/ for review):
- Do a feedforward pass for the current state s to get predicted Q-values for all actions.
- Do a feedforward pass for the next state s′ and calculate maximum over all network outputs

- Set Q-value target for action a to
 (use the max calculated in step 2). For all other actions, set the Q-value target to the same as originally returned from step 1, making the error 0 for those outputs.
(use the max calculated in step 2). For all other actions, set the Q-value target to the same as originally returned from step 1, making the error 0 for those outputs. - Update the weights using backpropagation.
If there is "reward" throughout the game, we can model the loss as

If the game is win/lose only ... most of the r's go away and the entire loss is based on a 0/1 or -1/1 score at the end of a game.
Practical Consideration 1: Experience Replay
To improve training, we cache all (or as much as possible) of the agent's state/move/reward/next-state data. Then, when we go to perform a training run, we can build a batch out of a subset of all previous moves. This provides diversity in the training data, whose value we discussed earlier.
Practical Consideration 2: Explore-Exploit Balance
In order to add more diversity to the agent's actions, we set a threshold ("epsilon") which represents the probability that the agent ignores its experience-based model and just chooses a random action. This also add diversity, by preventing the agent from taking an overly-narrow, 100% greedy (best-perfomance-so-far) path.
Let's Look at the Code!
Reinforcement learning code examples are a bit more complex than the other examples we've seen so far, because in the other examples, the data sets (training and test) exist outside the program as assets (e.g., the MNIST digit data).
In reinforcement learning, the training and reward data come from some environment that the agent is supposed to learn. Typically, the environment is simulated by local code, or represented by local code even if the real environment is remote or comes from the physical world via sensors.
So the code contains not just the neural net and training logic, but part (or all) of a game world itself.
One of the most elegant small, but complete, examples comes courtesy of former Ph.D. researcher (Univ. of Florida) and Apple rockstar Eder Santana. It's a simplified catch-the-falling-brick game (a bit like Atari Kaboom! but even simpler) that nevertheless is complex enough to illustrate DQL and to be impressive in action.
When we're done, we'll basically have a game, and an agent that plays, which run like this:

First, let's get familiar with the game environment itself, since we'll need to see how it works, before we can focus on the reinforcement learning part of the program.
class Catch(object):
def __init__(self, grid_size=10):
self.grid_size = grid_size
self.reset()
def _update_state(self, action):
"""
Input: action and states
Ouput: new states and reward
"""
state = self.state
if action == 0: # left
action = -1
elif action == 1: # stay
action = 0
else:
action = 1 # right
f0, f1, basket = state[0]
new_basket = min(max(1, basket + action), self.grid_size-1)
f0 += 1
out = np.asarray([f0, f1, new_basket])
out = out[np.newaxis]
assert len(out.shape) == 2
self.state = out
def _draw_state(self):
im_size = (self.grid_size,)*2
state = self.state[0]
canvas = np.zeros(im_size)
canvas[state[0], state[1]] = 1 # draw fruit
canvas[-1, state[2]-1:state[2] + 2] = 1 # draw basket
return canvas
def _get_reward(self):
fruit_row, fruit_col, basket = self.state[0]
if fruit_row == self.grid_size-1:
if abs(fruit_col - basket) <= 1:
return 1
else:
return -1
else:
return 0
def _is_over(self):
if self.state[0, 0] == self.grid_size-1:
return True
else:
return False
def observe(self):
canvas = self._draw_state()
return canvas.reshape((1, -1))
def act(self, action):
self._update_state(action)
reward = self._get_reward()
game_over = self._is_over()
return self.observe(), reward, game_over
def reset(self):
n = np.random.randint(0, self.grid_size-1, size=1)
m = np.random.randint(1, self.grid_size-2, size=1)
self.state = np.array([0, n, m])[np.newaxis].astype('int64')
Next, let's look at the network itself -- it's super simple, so we can get that out of the way too:
model = Sequential()
model.add(Dense(hidden_size, input_shape=(grid_size**2,), activation='relu'))
model.add(Dense(hidden_size, activation='relu'))
model.add(Dense(num_actions))
model.compile(sgd(lr=.2), "mse")
Note that the output layer has num_actions neurons.
We are going to implement the training target as
- the estimated reward for the one action taken when the game doesn't conclude, or
- error/reward for the specific action that loses/wins a game
In any case, we only train with an error/reward for actions the agent actually chose. We neutralize the hypothetical rewards for other actions, as they are not causally chained to any ground truth.
Next, let's zoom in on at the main game training loop:
win_cnt = 0
for e in range(epoch):
loss = 0.
env.reset()
game_over = False
# get initial input
input_t = env.observe()
while not game_over:
input_tm1 = input_t
# get next action
if np.random.rand() <= epsilon:
action = np.random.randint(0, num_actions, size=1)
else:
q = model.predict(input_tm1)
action = np.argmax(q[0])
# apply action, get rewards and new state
input_t, reward, game_over = env.act(action)
if reward == 1:
win_cnt += 1
# store experience
exp_replay.remember([input_tm1, action, reward, input_t], game_over)
# adapt model
inputs, targets = exp_replay.get_batch(model, batch_size=batch_size)
loss += model.train_on_batch(inputs, targets)
print("Epoch {:03d}/{:d} | Loss {:.4f} | Win count {}".format(e, epoch - 1, loss, win_cnt))
The key bits are:
- Choose an action
- Act and collect the reward and new state
- Cache previous state, action, reward, and new state in "Experience Replay" buffer
- Ask buffer for a batch of action data to train on
- Call
model.train_on_batchto perform one training batch
Last, let's dive into where the actual Q-Learning calculations occur, which happen, in this code to be in the get_batch call to the experience replay buffer object:
class ExperienceReplay(object):
def __init__(self, max_memory=100, discount=.9):
self.max_memory = max_memory
self.memory = list()
self.discount = discount
def remember(self, states, game_over):
# memory[i] = [[state_t, action_t, reward_t, state_t+1], game_over?]
self.memory.append([states, game_over])
if len(self.memory) > self.max_memory:
del self.memory[0]
def get_batch(self, model, batch_size=10):
len_memory = len(self.memory)
num_actions = model.output_shape[-1]
env_dim = self.memory[0][0][0].shape[1]
inputs = np.zeros((min(len_memory, batch_size), env_dim))
targets = np.zeros((inputs.shape[0], num_actions))
for i, idx in enumerate(np.random.randint(0, len_memory,
size=inputs.shape[0])):
state_t, action_t, reward_t, state_tp1 = self.memory[idx][0]
game_over = self.memory[idx][1]
inputs[i:i+1] = state_t
# There should be no target values for actions not taken.
# Thou shalt not correct actions not taken #deep
targets[i] = model.predict(state_t)[0]
Q_sa = np.max(model.predict(state_tp1)[0])
if game_over: # if game_over is True
targets[i, action_t] = reward_t
else:
# reward_t + gamma * max_a' Q(s', a')
targets[i, action_t] = reward_t + self.discount * Q_sa
return inputs, targets
The key bits here are:
- Set up "blank" buffers for a set of items of the requested batch size, or all memory, whichever is less (in case we don't have much data yet)
- one buffer is
inputs-- it will contain the game state or screen before the agent acted - the other buffer is
targets-- it will contain a vector of rewards-per-action (with just one non-zero entry, for the action the agent actually took)
- one buffer is
- Based on that batch size, randomly select records from memory
- For each of those cached records (which contain initial state, action, next state, and reward),
- Insert the initial game state into the proper place in the
inputsbuffer - If the action ended the game then:
- Insert a vector into
targetswith the real reward in the position of the action chosen
- Insert a vector into
- Else (if the action did not end the game):
- Insert a vector into
targetswith the following value in the position of the action taken:- (real reward)
- + (discount factor)(predicted-reward-for-best-action-in-the-next-state)
- Note: although the Q-Learning formula is implemented in the general version here, this specific game only produces reward when the game is over, so the "real reward" in this branch will always be zero
- Insert a vector into
- Insert the initial game state into the proper place in the
mkdir /dbfs/keras_rl
mkdir /dbfs/keras_rl/images
Ok, now let's run the main training script and teach Keras to play Catch:
import json
import numpy as np
from keras.models import Sequential
from keras.layers.core import Dense
from keras.optimizers import sgd
import collections
epsilon = .1 # exploration
num_actions = 3 # [move_left, stay, move_right]
epoch = 400
max_memory = 500
hidden_size = 100
batch_size = 50
grid_size = 10
model = Sequential()
model.add(Dense(hidden_size, input_shape=(grid_size**2,), activation='relu'))
model.add(Dense(hidden_size, activation='relu'))
model.add(Dense(num_actions))
model.compile(loss='mse', optimizer='adam')
# Define environment/gamedsadkjsa
env = Catch(grid_size)
# Initialize experience replay object
exp_replay = ExperienceReplay(max_memory=max_memory)
# Train
win_cnt = 0
last_ten = collections.deque(maxlen=10)
for e in range(epoch):
loss = 0.
env.reset()
game_over = False
# get initial input
input_t = env.observe()
while not game_over:
input_tm1 = input_t
# get next action
if np.random.rand() <= epsilon:
action = np.random.randint(0, num_actions, size=1)
else:
q = model.predict(input_tm1)
action = np.argmax(q[0])
# apply action, get rewards and new state
input_t, reward, game_over = env.act(action)
if reward == 1:
win_cnt += 1
# store experience
exp_replay.remember([input_tm1, action, reward, input_t], game_over)
# adapt model
inputs, targets = exp_replay.get_batch(model, batch_size=batch_size)
loss += model.train_on_batch(inputs, targets)
last_ten.append((reward+1)/2)
print("Epoch {:03d}/{:d} | Loss {:.4f} | Win count {} | Last 10 win rate {}".format(e, epoch - 1, loss, win_cnt, sum(last_ten)/10.0))
# Save trained model weights and architecture
model.save_weights("/tmp/model.h5", overwrite=True) #Issue with mounting on dbfs with save_weights. Workaround: saving locally to tmp then moving the files to dbfs in next cmd
with open("/tmp/model.json", "w") as outfile:
json.dump(model.to_json(), outfile)
Using TensorFlow backend.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /databricks/python/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Epoch 000/399 | Loss 0.0043 | Win count 0 | Last 10 win rate 0.0
Epoch 001/399 | Loss 0.1899 | Win count 1 | Last 10 win rate 0.1
Epoch 002/399 | Loss 0.1435 | Win count 1 | Last 10 win rate 0.1
Epoch 003/399 | Loss 0.1588 | Win count 2 | Last 10 win rate 0.2
Epoch 004/399 | Loss 0.0893 | Win count 3 | Last 10 win rate 0.3
Epoch 005/399 | Loss 0.0720 | Win count 4 | Last 10 win rate 0.4
Epoch 006/399 | Loss 0.0659 | Win count 5 | Last 10 win rate 0.5
Epoch 007/399 | Loss 0.0558 | Win count 5 | Last 10 win rate 0.5
Epoch 008/399 | Loss 0.1101 | Win count 5 | Last 10 win rate 0.5
Epoch 009/399 | Loss 0.1712 | Win count 6 | Last 10 win rate 0.6
Epoch 010/399 | Loss 0.0646 | Win count 6 | Last 10 win rate 0.6
Epoch 011/399 | Loss 0.1006 | Win count 6 | Last 10 win rate 0.5
Epoch 012/399 | Loss 0.1446 | Win count 6 | Last 10 win rate 0.5
Epoch 013/399 | Loss 0.1054 | Win count 6 | Last 10 win rate 0.4
Epoch 014/399 | Loss 0.1211 | Win count 6 | Last 10 win rate 0.3
Epoch 015/399 | Loss 0.1579 | Win count 6 | Last 10 win rate 0.2
Epoch 016/399 | Loss 0.1697 | Win count 6 | Last 10 win rate 0.1
Epoch 017/399 | Loss 0.0739 | Win count 6 | Last 10 win rate 0.1
Epoch 018/399 | Loss 0.0861 | Win count 6 | Last 10 win rate 0.1
Epoch 019/399 | Loss 0.1241 | Win count 6 | Last 10 win rate 0.0
Epoch 020/399 | Loss 0.0974 | Win count 6 | Last 10 win rate 0.0
Epoch 021/399 | Loss 0.0674 | Win count 6 | Last 10 win rate 0.0
Epoch 022/399 | Loss 0.0464 | Win count 6 | Last 10 win rate 0.0
Epoch 023/399 | Loss 0.0580 | Win count 6 | Last 10 win rate 0.0
Epoch 024/399 | Loss 0.0385 | Win count 6 | Last 10 win rate 0.0
Epoch 025/399 | Loss 0.0270 | Win count 6 | Last 10 win rate 0.0
Epoch 026/399 | Loss 0.0298 | Win count 6 | Last 10 win rate 0.0
Epoch 027/399 | Loss 0.0355 | Win count 6 | Last 10 win rate 0.0
Epoch 028/399 | Loss 0.0276 | Win count 6 | Last 10 win rate 0.0
Epoch 029/399 | Loss 0.0165 | Win count 6 | Last 10 win rate 0.0
Epoch 030/399 | Loss 0.0338 | Win count 6 | Last 10 win rate 0.0
Epoch 031/399 | Loss 0.0265 | Win count 7 | Last 10 win rate 0.1
Epoch 032/399 | Loss 0.0395 | Win count 7 | Last 10 win rate 0.1
Epoch 033/399 | Loss 0.0457 | Win count 7 | Last 10 win rate 0.1
Epoch 034/399 | Loss 0.0387 | Win count 7 | Last 10 win rate 0.1
Epoch 035/399 | Loss 0.0275 | Win count 8 | Last 10 win rate 0.2
Epoch 036/399 | Loss 0.0347 | Win count 8 | Last 10 win rate 0.2
Epoch 037/399 | Loss 0.0365 | Win count 8 | Last 10 win rate 0.2
Epoch 038/399 | Loss 0.0283 | Win count 8 | Last 10 win rate 0.2
Epoch 039/399 | Loss 0.0222 | Win count 9 | Last 10 win rate 0.3
Epoch 040/399 | Loss 0.0211 | Win count 9 | Last 10 win rate 0.3
Epoch 041/399 | Loss 0.0439 | Win count 9 | Last 10 win rate 0.2
Epoch 042/399 | Loss 0.0303 | Win count 9 | Last 10 win rate 0.2
Epoch 043/399 | Loss 0.0270 | Win count 9 | Last 10 win rate 0.2
Epoch 044/399 | Loss 0.0163 | Win count 10 | Last 10 win rate 0.3
Epoch 045/399 | Loss 0.0469 | Win count 11 | Last 10 win rate 0.3
Epoch 046/399 | Loss 0.0212 | Win count 12 | Last 10 win rate 0.4
Epoch 047/399 | Loss 0.0198 | Win count 13 | Last 10 win rate 0.5
Epoch 048/399 | Loss 0.0418 | Win count 13 | Last 10 win rate 0.5
Epoch 049/399 | Loss 0.0344 | Win count 14 | Last 10 win rate 0.5
Epoch 050/399 | Loss 0.0353 | Win count 14 | Last 10 win rate 0.5
Epoch 051/399 | Loss 0.0359 | Win count 14 | Last 10 win rate 0.5
Epoch 052/399 | Loss 0.0258 | Win count 14 | Last 10 win rate 0.5
Epoch 053/399 | Loss 0.0413 | Win count 14 | Last 10 win rate 0.5
Epoch 054/399 | Loss 0.0277 | Win count 14 | Last 10 win rate 0.4
Epoch 055/399 | Loss 0.0270 | Win count 15 | Last 10 win rate 0.4
Epoch 056/399 | Loss 0.0214 | Win count 16 | Last 10 win rate 0.4
Epoch 057/399 | Loss 0.0227 | Win count 16 | Last 10 win rate 0.3
Epoch 058/399 | Loss 0.0183 | Win count 16 | Last 10 win rate 0.3
Epoch 059/399 | Loss 0.0260 | Win count 16 | Last 10 win rate 0.2
Epoch 060/399 | Loss 0.0210 | Win count 17 | Last 10 win rate 0.3
Epoch 061/399 | Loss 0.0335 | Win count 17 | Last 10 win rate 0.3
Epoch 062/399 | Loss 0.0261 | Win count 18 | Last 10 win rate 0.4
Epoch 063/399 | Loss 0.0362 | Win count 18 | Last 10 win rate 0.4
Epoch 064/399 | Loss 0.0223 | Win count 19 | Last 10 win rate 0.5
Epoch 065/399 | Loss 0.0689 | Win count 20 | Last 10 win rate 0.5
Epoch 066/399 | Loss 0.0211 | Win count 20 | Last 10 win rate 0.4
Epoch 067/399 | Loss 0.0330 | Win count 21 | Last 10 win rate 0.5
Epoch 068/399 | Loss 0.0407 | Win count 22 | Last 10 win rate 0.6
Epoch 069/399 | Loss 0.0302 | Win count 22 | Last 10 win rate 0.6
Epoch 070/399 | Loss 0.0298 | Win count 22 | Last 10 win rate 0.5
Epoch 071/399 | Loss 0.0277 | Win count 23 | Last 10 win rate 0.6
Epoch 072/399 | Loss 0.0241 | Win count 24 | Last 10 win rate 0.6
Epoch 073/399 | Loss 0.0437 | Win count 24 | Last 10 win rate 0.6
Epoch 074/399 | Loss 0.0327 | Win count 24 | Last 10 win rate 0.5
Epoch 075/399 | Loss 0.0223 | Win count 24 | Last 10 win rate 0.4
Epoch 076/399 | Loss 0.0235 | Win count 24 | Last 10 win rate 0.4
Epoch 077/399 | Loss 0.0344 | Win count 25 | Last 10 win rate 0.4
Epoch 078/399 | Loss 0.0399 | Win count 26 | Last 10 win rate 0.4
Epoch 079/399 | Loss 0.0260 | Win count 27 | Last 10 win rate 0.5
Epoch 080/399 | Loss 0.0296 | Win count 27 | Last 10 win rate 0.5
Epoch 081/399 | Loss 0.0296 | Win count 28 | Last 10 win rate 0.5
Epoch 082/399 | Loss 0.0232 | Win count 28 | Last 10 win rate 0.4
Epoch 083/399 | Loss 0.0229 | Win count 28 | Last 10 win rate 0.4
Epoch 084/399 | Loss 0.0473 | Win count 28 | Last 10 win rate 0.4
Epoch 085/399 | Loss 0.0428 | Win count 29 | Last 10 win rate 0.5
Epoch 086/399 | Loss 0.0469 | Win count 30 | Last 10 win rate 0.6
Epoch 087/399 | Loss 0.0364 | Win count 31 | Last 10 win rate 0.6
Epoch 088/399 | Loss 0.0351 | Win count 31 | Last 10 win rate 0.5
Epoch 089/399 | Loss 0.0326 | Win count 31 | Last 10 win rate 0.4
Epoch 090/399 | Loss 0.0277 | Win count 32 | Last 10 win rate 0.5
Epoch 091/399 | Loss 0.0216 | Win count 32 | Last 10 win rate 0.4
Epoch 092/399 | Loss 0.0315 | Win count 33 | Last 10 win rate 0.5
Epoch 093/399 | Loss 0.0195 | Win count 34 | Last 10 win rate 0.6
Epoch 094/399 | Loss 0.0253 | Win count 34 | Last 10 win rate 0.6
Epoch 095/399 | Loss 0.0246 | Win count 34 | Last 10 win rate 0.5
Epoch 096/399 | Loss 0.0187 | Win count 34 | Last 10 win rate 0.4
Epoch 097/399 | Loss 0.0185 | Win count 35 | Last 10 win rate 0.4
Epoch 098/399 | Loss 0.0252 | Win count 36 | Last 10 win rate 0.5
Epoch 099/399 | Loss 0.0232 | Win count 36 | Last 10 win rate 0.5
Epoch 100/399 | Loss 0.0241 | Win count 36 | Last 10 win rate 0.4
Epoch 101/399 | Loss 0.0192 | Win count 36 | Last 10 win rate 0.4
Epoch 102/399 | Loss 0.0221 | Win count 36 | Last 10 win rate 0.3
Epoch 103/399 | Loss 0.0304 | Win count 37 | Last 10 win rate 0.3
Epoch 104/399 | Loss 0.0283 | Win count 38 | Last 10 win rate 0.4
Epoch 105/399 | Loss 0.0308 | Win count 38 | Last 10 win rate 0.4
Epoch 106/399 | Loss 0.0274 | Win count 38 | Last 10 win rate 0.4
Epoch 107/399 | Loss 0.0350 | Win count 39 | Last 10 win rate 0.4
Epoch 108/399 | Loss 0.0490 | Win count 39 | Last 10 win rate 0.3
Epoch 109/399 | Loss 0.0354 | Win count 39 | Last 10 win rate 0.3
Epoch 110/399 | Loss 0.0236 | Win count 39 | Last 10 win rate 0.3
Epoch 111/399 | Loss 0.0245 | Win count 39 | Last 10 win rate 0.3
Epoch 112/399 | Loss 0.0200 | Win count 40 | Last 10 win rate 0.4
Epoch 113/399 | Loss 0.0221 | Win count 40 | Last 10 win rate 0.3
Epoch 114/399 | Loss 0.0376 | Win count 40 | Last 10 win rate 0.2
Epoch 115/399 | Loss 0.0246 | Win count 40 | Last 10 win rate 0.2
Epoch 116/399 | Loss 0.0229 | Win count 41 | Last 10 win rate 0.3
Epoch 117/399 | Loss 0.0254 | Win count 42 | Last 10 win rate 0.3
Epoch 118/399 | Loss 0.0271 | Win count 43 | Last 10 win rate 0.4
Epoch 119/399 | Loss 0.0242 | Win count 44 | Last 10 win rate 0.5
Epoch 120/399 | Loss 0.0261 | Win count 45 | Last 10 win rate 0.6
Epoch 121/399 | Loss 0.0213 | Win count 46 | Last 10 win rate 0.7
Epoch 122/399 | Loss 0.0227 | Win count 47 | Last 10 win rate 0.7
Epoch 123/399 | Loss 0.0175 | Win count 48 | Last 10 win rate 0.8
Epoch 124/399 | Loss 0.0134 | Win count 49 | Last 10 win rate 0.9
Epoch 125/399 | Loss 0.0146 | Win count 50 | Last 10 win rate 1.0
Epoch 126/399 | Loss 0.0107 | Win count 51 | Last 10 win rate 1.0
Epoch 127/399 | Loss 0.0129 | Win count 52 | Last 10 win rate 1.0
Epoch 128/399 | Loss 0.0193 | Win count 53 | Last 10 win rate 1.0
Epoch 129/399 | Loss 0.0183 | Win count 54 | Last 10 win rate 1.0
Epoch 130/399 | Loss 0.0140 | Win count 55 | Last 10 win rate 1.0
Epoch 131/399 | Loss 0.0158 | Win count 56 | Last 10 win rate 1.0
Epoch 132/399 | Loss 0.0129 | Win count 56 | Last 10 win rate 0.9
Epoch 133/399 | Loss 0.0180 | Win count 57 | Last 10 win rate 0.9
Epoch 134/399 | Loss 0.0174 | Win count 58 | Last 10 win rate 0.9
Epoch 135/399 | Loss 0.0232 | Win count 59 | Last 10 win rate 0.9
Epoch 136/399 | Loss 0.0178 | Win count 60 | Last 10 win rate 0.9
Epoch 137/399 | Loss 0.0195 | Win count 61 | Last 10 win rate 0.9
Epoch 138/399 | Loss 0.0157 | Win count 62 | Last 10 win rate 0.9
Epoch 139/399 | Loss 0.0217 | Win count 63 | Last 10 win rate 0.9
Epoch 140/399 | Loss 0.0166 | Win count 64 | Last 10 win rate 0.9
Epoch 141/399 | Loss 0.0601 | Win count 65 | Last 10 win rate 0.9
Epoch 142/399 | Loss 0.0388 | Win count 66 | Last 10 win rate 1.0
Epoch 143/399 | Loss 0.0353 | Win count 67 | Last 10 win rate 1.0
Epoch 144/399 | Loss 0.0341 | Win count 68 | Last 10 win rate 1.0
Epoch 145/399 | Loss 0.0237 | Win count 69 | Last 10 win rate 1.0
Epoch 146/399 | Loss 0.0250 | Win count 70 | Last 10 win rate 1.0
Epoch 147/399 | Loss 0.0163 | Win count 70 | Last 10 win rate 0.9
Epoch 148/399 | Loss 0.0224 | Win count 71 | Last 10 win rate 0.9
Epoch 149/399 | Loss 0.0194 | Win count 72 | Last 10 win rate 0.9
Epoch 150/399 | Loss 0.0133 | Win count 72 | Last 10 win rate 0.8
Epoch 151/399 | Loss 0.0126 | Win count 72 | Last 10 win rate 0.7
Epoch 152/399 | Loss 0.0183 | Win count 73 | Last 10 win rate 0.7
Epoch 153/399 | Loss 0.0131 | Win count 74 | Last 10 win rate 0.7
Epoch 154/399 | Loss 0.0216 | Win count 75 | Last 10 win rate 0.7
Epoch 155/399 | Loss 0.0169 | Win count 76 | Last 10 win rate 0.7
Epoch 156/399 | Loss 0.0130 | Win count 76 | Last 10 win rate 0.6
Epoch 157/399 | Loss 0.0434 | Win count 77 | Last 10 win rate 0.7
Epoch 158/399 | Loss 0.0595 | Win count 78 | Last 10 win rate 0.7
Epoch 159/399 | Loss 0.0277 | Win count 79 | Last 10 win rate 0.7
Epoch 160/399 | Loss 0.0302 | Win count 80 | Last 10 win rate 0.8
Epoch 161/399 | Loss 0.0308 | Win count 81 | Last 10 win rate 0.9
Epoch 162/399 | Loss 0.0200 | Win count 81 | Last 10 win rate 0.8
Epoch 163/399 | Loss 0.0230 | Win count 81 | Last 10 win rate 0.7
Epoch 164/399 | Loss 0.0303 | Win count 81 | Last 10 win rate 0.6
Epoch 165/399 | Loss 0.0279 | Win count 82 | Last 10 win rate 0.6
Epoch 166/399 | Loss 0.0147 | Win count 83 | Last 10 win rate 0.7
Epoch 167/399 | Loss 0.0181 | Win count 84 | Last 10 win rate 0.7
Epoch 168/399 | Loss 0.0197 | Win count 84 | Last 10 win rate 0.6
Epoch 169/399 | Loss 0.0175 | Win count 85 | Last 10 win rate 0.6
Epoch 170/399 | Loss 0.0195 | Win count 86 | Last 10 win rate 0.6
Epoch 171/399 | Loss 0.0089 | Win count 87 | Last 10 win rate 0.6
Epoch 172/399 | Loss 0.0098 | Win count 88 | Last 10 win rate 0.7
Epoch 173/399 | Loss 0.0150 | Win count 89 | Last 10 win rate 0.8
Epoch 174/399 | Loss 0.0089 | Win count 90 | Last 10 win rate 0.9
Epoch 175/399 | Loss 0.0096 | Win count 91 | Last 10 win rate 0.9
Epoch 176/399 | Loss 0.0079 | Win count 91 | Last 10 win rate 0.8
Epoch 177/399 | Loss 0.0505 | Win count 92 | Last 10 win rate 0.8
Epoch 178/399 | Loss 0.0286 | Win count 93 | Last 10 win rate 0.9
Epoch 179/399 | Loss 0.0237 | Win count 94 | Last 10 win rate 0.9
Epoch 180/399 | Loss 0.0194 | Win count 94 | Last 10 win rate 0.8
Epoch 181/399 | Loss 0.0164 | Win count 95 | Last 10 win rate 0.8
Epoch 182/399 | Loss 0.0149 | Win count 95 | Last 10 win rate 0.7
Epoch 183/399 | Loss 0.0168 | Win count 96 | Last 10 win rate 0.7
Epoch 184/399 | Loss 0.0283 | Win count 97 | Last 10 win rate 0.7
Epoch 185/399 | Loss 0.0204 | Win count 98 | Last 10 win rate 0.7
Epoch 186/399 | Loss 0.0180 | Win count 99 | Last 10 win rate 0.8
Epoch 187/399 | Loss 0.0160 | Win count 100 | Last 10 win rate 0.8
Epoch 188/399 | Loss 0.0130 | Win count 100 | Last 10 win rate 0.7
Epoch 189/399 | Loss 0.0135 | Win count 101 | Last 10 win rate 0.7
Epoch 190/399 | Loss 0.0232 | Win count 102 | Last 10 win rate 0.8
Epoch 191/399 | Loss 0.0203 | Win count 103 | Last 10 win rate 0.8
Epoch 192/399 | Loss 0.0154 | Win count 104 | Last 10 win rate 0.9
Epoch 193/399 | Loss 0.0157 | Win count 105 | Last 10 win rate 0.9
Epoch 194/399 | Loss 0.0145 | Win count 106 | Last 10 win rate 0.9
Epoch 195/399 | Loss 0.0142 | Win count 107 | Last 10 win rate 0.9
Epoch 196/399 | Loss 0.0194 | Win count 107 | Last 10 win rate 0.8
Epoch 197/399 | Loss 0.0125 | Win count 108 | Last 10 win rate 0.8
Epoch 198/399 | Loss 0.0109 | Win count 109 | Last 10 win rate 0.9
Epoch 199/399 | Loss 0.0077 | Win count 110 | Last 10 win rate 0.9
Epoch 200/399 | Loss 0.0095 | Win count 111 | Last 10 win rate 0.9
Epoch 201/399 | Loss 0.0091 | Win count 112 | Last 10 win rate 0.9
Epoch 202/399 | Loss 0.0107 | Win count 113 | Last 10 win rate 0.9
Epoch 203/399 | Loss 0.0059 | Win count 114 | Last 10 win rate 0.9
Epoch 204/399 | Loss 0.0070 | Win count 115 | Last 10 win rate 0.9
Epoch 205/399 | Loss 0.0060 | Win count 116 | Last 10 win rate 0.9
Epoch 206/399 | Loss 0.0053 | Win count 117 | Last 10 win rate 1.0
Epoch 207/399 | Loss 0.0064 | Win count 118 | Last 10 win rate 1.0
Epoch 208/399 | Loss 0.0129 | Win count 119 | Last 10 win rate 1.0
Epoch 209/399 | Loss 0.0052 | Win count 119 | Last 10 win rate 0.9
Epoch 210/399 | Loss 0.0124 | Win count 120 | Last 10 win rate 0.9
Epoch 211/399 | Loss 0.0056 | Win count 120 | Last 10 win rate 0.8
Epoch 212/399 | Loss 0.0088 | Win count 120 | Last 10 win rate 0.7
Epoch 213/399 | Loss 0.0325 | Win count 121 | Last 10 win rate 0.7
Epoch 214/399 | Loss 0.0373 | Win count 121 | Last 10 win rate 0.6
Epoch 215/399 | Loss 0.0246 | Win count 122 | Last 10 win rate 0.6
Epoch 216/399 | Loss 0.0426 | Win count 123 | Last 10 win rate 0.6
Epoch 217/399 | Loss 0.0606 | Win count 124 | Last 10 win rate 0.6
Epoch 218/399 | Loss 0.0362 | Win count 125 | Last 10 win rate 0.6
Epoch 219/399 | Loss 0.0241 | Win count 126 | Last 10 win rate 0.7
Epoch 220/399 | Loss 0.0169 | Win count 127 | Last 10 win rate 0.7
Epoch 221/399 | Loss 0.0195 | Win count 128 | Last 10 win rate 0.8
Epoch 222/399 | Loss 0.0159 | Win count 129 | Last 10 win rate 0.9
Epoch 223/399 | Loss 0.0135 | Win count 130 | Last 10 win rate 0.9
Epoch 224/399 | Loss 0.0111 | Win count 131 | Last 10 win rate 1.0
Epoch 225/399 | Loss 0.0111 | Win count 132 | Last 10 win rate 1.0
Epoch 226/399 | Loss 0.0135 | Win count 133 | Last 10 win rate 1.0
Epoch 227/399 | Loss 0.0145 | Win count 134 | Last 10 win rate 1.0
Epoch 228/399 | Loss 0.0139 | Win count 135 | Last 10 win rate 1.0
Epoch 229/399 | Loss 0.0116 | Win count 136 | Last 10 win rate 1.0
Epoch 230/399 | Loss 0.0085 | Win count 137 | Last 10 win rate 1.0
Epoch 231/399 | Loss 0.0070 | Win count 138 | Last 10 win rate 1.0
Epoch 232/399 | Loss 0.0071 | Win count 139 | Last 10 win rate 1.0
Epoch 233/399 | Loss 0.0082 | Win count 140 | Last 10 win rate 1.0
Epoch 234/399 | Loss 0.0085 | Win count 141 | Last 10 win rate 1.0
Epoch 235/399 | Loss 0.0058 | Win count 142 | Last 10 win rate 1.0
Epoch 236/399 | Loss 0.0068 | Win count 143 | Last 10 win rate 1.0
Epoch 237/399 | Loss 0.0074 | Win count 144 | Last 10 win rate 1.0
Epoch 238/399 | Loss 0.0066 | Win count 145 | Last 10 win rate 1.0
Epoch 239/399 | Loss 0.0060 | Win count 146 | Last 10 win rate 1.0
Epoch 240/399 | Loss 0.0074 | Win count 147 | Last 10 win rate 1.0
Epoch 241/399 | Loss 0.0306 | Win count 148 | Last 10 win rate 1.0
Epoch 242/399 | Loss 0.0155 | Win count 148 | Last 10 win rate 0.9
Epoch 243/399 | Loss 0.0122 | Win count 149 | Last 10 win rate 0.9
Epoch 244/399 | Loss 0.0100 | Win count 150 | Last 10 win rate 0.9
Epoch 245/399 | Loss 0.0068 | Win count 151 | Last 10 win rate 0.9
Epoch 246/399 | Loss 0.0328 | Win count 152 | Last 10 win rate 0.9
Epoch 247/399 | Loss 0.0415 | Win count 153 | Last 10 win rate 0.9
Epoch 248/399 | Loss 0.0638 | Win count 153 | Last 10 win rate 0.8
Epoch 249/399 | Loss 0.0527 | Win count 154 | Last 10 win rate 0.8
Epoch 250/399 | Loss 0.0359 | Win count 155 | Last 10 win rate 0.8
Epoch 251/399 | Loss 0.0224 | Win count 156 | Last 10 win rate 0.8
Epoch 252/399 | Loss 0.0482 | Win count 157 | Last 10 win rate 0.9
Epoch 253/399 | Loss 0.0212 | Win count 157 | Last 10 win rate 0.8
Epoch 254/399 | Loss 0.0372 | Win count 158 | Last 10 win rate 0.8
Epoch 255/399 | Loss 0.0235 | Win count 159 | Last 10 win rate 0.8
Epoch 256/399 | Loss 0.0196 | Win count 159 | Last 10 win rate 0.7
Epoch 257/399 | Loss 0.0272 | Win count 160 | Last 10 win rate 0.7
Epoch 258/399 | Loss 0.0300 | Win count 161 | Last 10 win rate 0.8
Epoch 259/399 | Loss 0.0232 | Win count 162 | Last 10 win rate 0.8
Epoch 260/399 | Loss 0.0501 | Win count 163 | Last 10 win rate 0.8
Epoch 261/399 | Loss 0.0176 | Win count 164 | Last 10 win rate 0.8
Epoch 262/399 | Loss 0.0107 | Win count 165 | Last 10 win rate 0.8
Epoch 263/399 | Loss 0.0113 | Win count 166 | Last 10 win rate 0.9
Epoch 264/399 | Loss 0.0093 | Win count 167 | Last 10 win rate 0.9
Epoch 265/399 | Loss 0.0116 | Win count 168 | Last 10 win rate 0.9
Epoch 266/399 | Loss 0.0099 | Win count 169 | Last 10 win rate 1.0
Epoch 267/399 | Loss 0.0071 | Win count 170 | Last 10 win rate 1.0
Epoch 268/399 | Loss 0.0071 | Win count 171 | Last 10 win rate 1.0
Epoch 269/399 | Loss 0.0056 | Win count 172 | Last 10 win rate 1.0
Epoch 270/399 | Loss 0.0043 | Win count 173 | Last 10 win rate 1.0
Epoch 271/399 | Loss 0.0037 | Win count 174 | Last 10 win rate 1.0
Epoch 272/399 | Loss 0.0028 | Win count 175 | Last 10 win rate 1.0
Epoch 273/399 | Loss 0.0032 | Win count 176 | Last 10 win rate 1.0
Epoch 274/399 | Loss 0.0127 | Win count 177 | Last 10 win rate 1.0
Epoch 275/399 | Loss 0.0057 | Win count 178 | Last 10 win rate 1.0
Epoch 276/399 | Loss 0.0044 | Win count 179 | Last 10 win rate 1.0
Epoch 277/399 | Loss 0.0042 | Win count 180 | Last 10 win rate 1.0
Epoch 278/399 | Loss 0.0035 | Win count 181 | Last 10 win rate 1.0
Epoch 279/399 | Loss 0.0036 | Win count 182 | Last 10 win rate 1.0
Epoch 280/399 | Loss 0.0037 | Win count 183 | Last 10 win rate 1.0
Epoch 281/399 | Loss 0.0026 | Win count 184 | Last 10 win rate 1.0
Epoch 282/399 | Loss 0.0026 | Win count 185 | Last 10 win rate 1.0
Epoch 283/399 | Loss 0.0019 | Win count 186 | Last 10 win rate 1.0
Epoch 284/399 | Loss 0.0030 | Win count 187 | Last 10 win rate 1.0
Epoch 285/399 | Loss 0.0019 | Win count 188 | Last 10 win rate 1.0
Epoch 286/399 | Loss 0.0021 | Win count 189 | Last 10 win rate 1.0
Epoch 287/399 | Loss 0.0020 | Win count 190 | Last 10 win rate 1.0
Epoch 288/399 | Loss 0.0017 | Win count 191 | Last 10 win rate 1.0
Epoch 289/399 | Loss 0.0019 | Win count 192 | Last 10 win rate 1.0
Epoch 290/399 | Loss 0.0015 | Win count 193 | Last 10 win rate 1.0
Epoch 291/399 | Loss 0.0021 | Win count 194 | Last 10 win rate 1.0
Epoch 292/399 | Loss 0.0019 | Win count 195 | Last 10 win rate 1.0
Epoch 293/399 | Loss 0.0012 | Win count 196 | Last 10 win rate 1.0
Epoch 294/399 | Loss 0.0297 | Win count 197 | Last 10 win rate 1.0
Epoch 295/399 | Loss 0.0068 | Win count 198 | Last 10 win rate 1.0
Epoch 296/399 | Loss 0.0050 | Win count 199 | Last 10 win rate 1.0
Epoch 297/399 | Loss 0.0040 | Win count 200 | Last 10 win rate 1.0
Epoch 298/399 | Loss 0.0052 | Win count 201 | Last 10 win rate 1.0
Epoch 299/399 | Loss 0.0034 | Win count 202 | Last 10 win rate 1.0
Epoch 300/399 | Loss 0.0029 | Win count 203 | Last 10 win rate 1.0
Epoch 301/399 | Loss 0.0034 | Win count 203 | Last 10 win rate 0.9
Epoch 302/399 | Loss 0.0313 | Win count 204 | Last 10 win rate 0.9
Epoch 303/399 | Loss 0.0042 | Win count 205 | Last 10 win rate 0.9
Epoch 304/399 | Loss 0.0224 | Win count 206 | Last 10 win rate 0.9
Epoch 305/399 | Loss 0.0275 | Win count 207 | Last 10 win rate 0.9
Epoch 306/399 | Loss 0.0345 | Win count 208 | Last 10 win rate 0.9
Epoch 307/399 | Loss 0.0138 | Win count 209 | Last 10 win rate 0.9
Epoch 308/399 | Loss 0.0129 | Win count 209 | Last 10 win rate 0.8
Epoch 309/399 | Loss 0.0151 | Win count 210 | Last 10 win rate 0.8
Epoch 310/399 | Loss 0.0337 | Win count 211 | Last 10 win rate 0.8
Epoch 311/399 | Loss 0.0167 | Win count 212 | Last 10 win rate 0.9
Epoch 312/399 | Loss 0.0171 | Win count 213 | Last 10 win rate 0.9
Epoch 313/399 | Loss 0.0088 | Win count 214 | Last 10 win rate 0.9
Epoch 314/399 | Loss 0.0096 | Win count 215 | Last 10 win rate 0.9
Epoch 315/399 | Loss 0.0078 | Win count 215 | Last 10 win rate 0.8
Epoch 316/399 | Loss 0.0174 | Win count 216 | Last 10 win rate 0.8
Epoch 317/399 | Loss 0.0098 | Win count 217 | Last 10 win rate 0.8
Epoch 318/399 | Loss 0.0091 | Win count 218 | Last 10 win rate 0.9
Epoch 319/399 | Loss 0.0054 | Win count 219 | Last 10 win rate 0.9
Epoch 320/399 | Loss 0.0078 | Win count 220 | Last 10 win rate 0.9
Epoch 321/399 | Loss 0.0043 | Win count 221 | Last 10 win rate 0.9
Epoch 322/399 | Loss 0.0040 | Win count 222 | Last 10 win rate 0.9
Epoch 323/399 | Loss 0.0040 | Win count 223 | Last 10 win rate 0.9
Epoch 324/399 | Loss 0.0043 | Win count 224 | Last 10 win rate 0.9
Epoch 325/399 | Loss 0.0028 | Win count 225 | Last 10 win rate 1.0
Epoch 326/399 | Loss 0.0035 | Win count 226 | Last 10 win rate 1.0
Epoch 327/399 | Loss 0.0032 | Win count 227 | Last 10 win rate 1.0
Epoch 328/399 | Loss 0.0023 | Win count 228 | Last 10 win rate 1.0
Epoch 329/399 | Loss 0.0022 | Win count 229 | Last 10 win rate 1.0
Epoch 330/399 | Loss 0.0022 | Win count 230 | Last 10 win rate 1.0
Epoch 331/399 | Loss 0.0022 | Win count 231 | Last 10 win rate 1.0
Epoch 332/399 | Loss 0.0027 | Win count 232 | Last 10 win rate 1.0
Epoch 333/399 | Loss 0.0033 | Win count 233 | Last 10 win rate 1.0
Epoch 334/399 | Loss 0.0022 | Win count 234 | Last 10 win rate 1.0
Epoch 335/399 | Loss 0.0018 | Win count 235 | Last 10 win rate 1.0
Epoch 336/399 | Loss 0.0032 | Win count 236 | Last 10 win rate 1.0
Epoch 337/399 | Loss 0.0025 | Win count 237 | Last 10 win rate 1.0
Epoch 338/399 | Loss 0.0019 | Win count 238 | Last 10 win rate 1.0
Epoch 339/399 | Loss 0.0018 | Win count 239 | Last 10 win rate 1.0
Epoch 340/399 | Loss 0.0020 | Win count 240 | Last 10 win rate 1.0
Epoch 341/399 | Loss 0.0019 | Win count 241 | Last 10 win rate 1.0
Epoch 342/399 | Loss 0.0014 | Win count 242 | Last 10 win rate 1.0
Epoch 343/399 | Loss 0.0015 | Win count 243 | Last 10 win rate 1.0
Epoch 344/399 | Loss 0.0017 | Win count 244 | Last 10 win rate 1.0
Epoch 345/399 | Loss 0.0016 | Win count 245 | Last 10 win rate 1.0
Epoch 346/399 | Loss 0.0011 | Win count 246 | Last 10 win rate 1.0
Epoch 347/399 | Loss 0.0013 | Win count 247 | Last 10 win rate 1.0
Epoch 348/399 | Loss 0.0016 | Win count 248 | Last 10 win rate 1.0
Epoch 349/399 | Loss 0.0010 | Win count 248 | Last 10 win rate 0.9
Epoch 350/399 | Loss 0.0012 | Win count 249 | Last 10 win rate 0.9
Epoch 351/399 | Loss 0.0029 | Win count 250 | Last 10 win rate 0.9
Epoch 352/399 | Loss 0.0017 | Win count 251 | Last 10 win rate 0.9
Epoch 353/399 | Loss 0.0019 | Win count 252 | Last 10 win rate 0.9
Epoch 354/399 | Loss 0.0032 | Win count 253 | Last 10 win rate 0.9
Epoch 355/399 | Loss 0.0010 | Win count 254 | Last 10 win rate 0.9
Epoch 356/399 | Loss 0.0013 | Win count 255 | Last 10 win rate 0.9
Epoch 357/399 | Loss 0.0017 | Win count 256 | Last 10 win rate 0.9
Epoch 358/399 | Loss 0.0015 | Win count 257 | Last 10 win rate 0.9
Epoch 359/399 | Loss 0.0010 | Win count 258 | Last 10 win rate 1.0
Epoch 360/399 | Loss 0.0008 | Win count 259 | Last 10 win rate 1.0
Epoch 361/399 | Loss 0.0018 | Win count 260 | Last 10 win rate 1.0
Epoch 362/399 | Loss 0.0016 | Win count 261 | Last 10 win rate 1.0
Epoch 363/399 | Loss 0.0013 | Win count 262 | Last 10 win rate 1.0
Epoch 364/399 | Loss 0.0016 | Win count 263 | Last 10 win rate 1.0
Epoch 365/399 | Loss 0.0020 | Win count 264 | Last 10 win rate 1.0
Epoch 366/399 | Loss 0.0011 | Win count 265 | Last 10 win rate 1.0
Epoch 367/399 | Loss 0.0015 | Win count 266 | Last 10 win rate 1.0
Epoch 368/399 | Loss 0.0009 | Win count 266 | Last 10 win rate 0.9
Epoch 369/399 | Loss 0.0117 | Win count 267 | Last 10 win rate 0.9
Epoch 370/399 | Loss 0.0037 | Win count 267 | Last 10 win rate 0.8
Epoch 371/399 | Loss 0.0146 | Win count 268 | Last 10 win rate 0.8
Epoch 372/399 | Loss 0.0101 | Win count 269 | Last 10 win rate 0.8
Epoch 373/399 | Loss 0.0035 | Win count 270 | Last 10 win rate 0.8
Epoch 374/399 | Loss 0.0031 | Win count 271 | Last 10 win rate 0.8
Epoch 375/399 | Loss 0.0055 | Win count 272 | Last 10 win rate 0.8
Epoch 376/399 | Loss 0.0044 | Win count 272 | Last 10 win rate 0.7
Epoch 377/399 | Loss 0.0223 | Win count 272 | Last 10 win rate 0.6
Epoch 378/399 | Loss 0.0214 | Win count 273 | Last 10 win rate 0.7
Epoch 379/399 | Loss 0.0291 | Win count 274 | Last 10 win rate 0.7
Epoch 380/399 | Loss 0.0218 | Win count 275 | Last 10 win rate 0.8
Epoch 381/399 | Loss 0.0188 | Win count 276 | Last 10 win rate 0.8
Epoch 382/399 | Loss 0.0108 | Win count 277 | Last 10 win rate 0.8
Epoch 383/399 | Loss 0.0102 | Win count 278 | Last 10 win rate 0.8
Epoch 384/399 | Loss 0.0074 | Win count 279 | Last 10 win rate 0.8
Epoch 385/399 | Loss 0.0074 | Win count 280 | Last 10 win rate 0.8
Epoch 386/399 | Loss 0.0068 | Win count 281 | Last 10 win rate 0.9
Epoch 387/399 | Loss 0.0168 | Win count 282 | Last 10 win rate 1.0
Epoch 388/399 | Loss 0.0113 | Win count 283 | Last 10 win rate 1.0
Epoch 389/399 | Loss 0.0114 | Win count 284 | Last 10 win rate 1.0
Epoch 390/399 | Loss 0.0127 | Win count 285 | Last 10 win rate 1.0
Epoch 391/399 | Loss 0.0085 | Win count 286 | Last 10 win rate 1.0
Epoch 392/399 | Loss 0.0098 | Win count 287 | Last 10 win rate 1.0
Epoch 393/399 | Loss 0.0074 | Win count 288 | Last 10 win rate 1.0
Epoch 394/399 | Loss 0.0054 | Win count 289 | Last 10 win rate 1.0
Epoch 395/399 | Loss 0.0050 | Win count 290 | Last 10 win rate 1.0
Epoch 396/399 | Loss 0.0041 | Win count 291 | Last 10 win rate 1.0
Epoch 397/399 | Loss 0.0032 | Win count 292 | Last 10 win rate 1.0
Epoch 398/399 | Loss 0.0029 | Win count 293 | Last 10 win rate 1.0
Epoch 399/399 | Loss 0.0025 | Win count 294 | Last 10 win rate 1.0
ls -la /tmp/
mv /tmp/model.h5 /dbfs/keras_rl/
mv /tmp/model.json /dbfs/keras_rl/
total 300
drwxrwxrwt 1 root root 4096 Feb 10 10:46 .
drwxr-xr-x 1 root root 4096 Feb 10 10:13 ..
drwxrwxrwt 2 root root 4096 Feb 10 10:13 .ICE-unix
drwxrwxrwt 2 root root 4096 Feb 10 10:13 .X11-unix
drwxr-xr-x 3 root root 4096 Feb 10 10:14 Rserv
drwx------ 2 root root 4096 Feb 10 10:14 Rtmp5coQwp
-rw-r--r-- 1 root root 22 Feb 10 10:13 chauffeur-daemon-params
-rw-r--r-- 1 root root 5 Feb 10 10:13 chauffeur-daemon.pid
-rw-r--r-- 1 ubuntu ubuntu 156 Feb 10 10:13 chauffeur-env.sh
-rw-r--r-- 1 ubuntu ubuntu 217 Feb 10 10:13 custom-spark.conf
-rw-r--r-- 1 root root 19 Feb 10 10:13 driver-daemon-params
-rw-r--r-- 1 root root 5 Feb 10 10:13 driver-daemon.pid
-rw-r--r-- 1 root root 2659 Feb 10 10:13 driver-env.sh
drwxr-xr-x 2 root root 4096 Feb 10 10:13 hsperfdata_root
-rw-r--r-- 1 root root 21 Feb 10 10:13 master-params
-rw-r--r-- 1 root root 95928 Feb 10 10:46 model.h5
-rw-r--r-- 1 root root 1832 Feb 10 10:46 model.json
-rw-r--r-- 1 root root 5 Feb 10 10:13 spark-root-org.apache.spark.deploy.master.Master-1.pid
-rw------- 1 root root 0 Feb 10 10:13 tmp.zaDTA1spCA
-rw------- 1 root root 136707 Feb 10 10:46 tmp7ov8uspv.png
ls -la /dbfs/keras_rl*
total 108
drwxrwxrwx 2 root root 4096 Feb 10 2021 .
drwxrwxrwx 2 root root 4096 Feb 10 10:46 ..
drwxrwxrwx 2 root root 4096 Feb 10 10:13 images
-rwxrwxrwx 1 root root 95928 Feb 10 2021 model.h5
-rwxrwxrwx 1 root root 1832 Feb 10 2021 model.json
import json
import matplotlib.pyplot as plt
import numpy as np
from keras.models import model_from_json
grid_size = 10
with open("/dbfs/keras_rl/model.json", "r") as jfile:
model = model_from_json(json.load(jfile))
model.load_weights("/dbfs/keras_rl/model.h5")
model.compile(loss='mse', optimizer='adam')
# Define environment, game
env = Catch(grid_size)
c = 0
for e in range(10):
loss = 0.
env.reset()
game_over = False
# get initial input
input_t = env.observe()
plt.imshow(input_t.reshape((grid_size,)*2),
interpolation='none', cmap='gray')
plt.savefig("/dbfs/keras_rl/images/%03d.png" % c)
c += 1
while not game_over:
input_tm1 = input_t
# get next action
q = model.predict(input_tm1)
action = np.argmax(q[0])
# apply action, get rewards and new state
input_t, reward, game_over = env.act(action)
plt.imshow(input_t.reshape((grid_size,)*2),
interpolation='none', cmap='gray')
plt.savefig("/dbfs/keras_rl/images/%03d.png" % c)
c += 1
ls -la /dbfs/keras_rl/images
total 608
drwxrwxrwx 2 root root 4096 Feb 10 11:01 .
drwxrwxrwx 2 root root 4096 Jan 12 13:46 ..
-rwxrwxrwx 1 root root 5789 Feb 10 10:46 000.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:46 001.png
-rwxrwxrwx 1 root root 5789 Feb 10 10:46 002.png
-rwxrwxrwx 1 root root 5765 Feb 10 10:46 003.png
-rwxrwxrwx 1 root root 5782 Feb 10 10:46 004.png
-rwxrwxrwx 1 root root 5769 Feb 10 10:46 005.png
-rwxrwxrwx 1 root root 5786 Feb 10 10:46 006.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:46 007.png
-rwxrwxrwx 1 root root 5777 Feb 10 10:46 008.png
-rwxrwxrwx 1 root root 5741 Feb 10 10:46 009.png
-rwxrwxrwx 1 root root 5789 Feb 10 10:46 010.png
-rwxrwxrwx 1 root root 5767 Feb 10 10:46 011.png
-rwxrwxrwx 1 root root 5791 Feb 10 10:46 012.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:46 013.png
-rwxrwxrwx 1 root root 5785 Feb 10 10:46 014.png
-rwxrwxrwx 1 root root 5769 Feb 10 10:46 015.png
-rwxrwxrwx 1 root root 5792 Feb 10 10:46 016.png
-rwxrwxrwx 1 root root 5770 Feb 10 10:46 017.png
-rwxrwxrwx 1 root root 5783 Feb 10 10:46 018.png
-rwxrwxrwx 1 root root 5745 Feb 10 10:46 019.png
-rwxrwxrwx 1 root root 5789 Feb 10 10:46 020.png
-rwxrwxrwx 1 root root 5767 Feb 10 10:46 021.png
-rwxrwxrwx 1 root root 5791 Feb 10 10:46 022.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:46 023.png
-rwxrwxrwx 1 root root 5785 Feb 10 10:47 024.png
-rwxrwxrwx 1 root root 5769 Feb 10 10:47 025.png
-rwxrwxrwx 1 root root 5792 Feb 10 10:47 026.png
-rwxrwxrwx 1 root root 5770 Feb 10 10:47 027.png
-rwxrwxrwx 1 root root 5783 Feb 10 10:47 028.png
-rwxrwxrwx 1 root root 5745 Feb 10 10:47 029.png
-rwxrwxrwx 1 root root 5788 Feb 10 10:47 030.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:47 031.png
-rwxrwxrwx 1 root root 5792 Feb 10 10:47 032.png
-rwxrwxrwx 1 root root 5767 Feb 10 10:47 033.png
-rwxrwxrwx 1 root root 5786 Feb 10 10:47 034.png
-rwxrwxrwx 1 root root 5770 Feb 10 10:48 035.png
-rwxrwxrwx 1 root root 5792 Feb 10 10:48 036.png
-rwxrwxrwx 1 root root 5769 Feb 10 10:48 037.png
-rwxrwxrwx 1 root root 5785 Feb 10 10:48 038.png
-rwxrwxrwx 1 root root 5743 Feb 10 10:48 039.png
-rwxrwxrwx 1 root root 5787 Feb 10 10:48 040.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:48 041.png
-rwxrwxrwx 1 root root 5786 Feb 10 10:48 042.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:49 043.png
-rwxrwxrwx 1 root root 5782 Feb 10 10:49 044.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:49 045.png
-rwxrwxrwx 1 root root 5785 Feb 10 10:49 046.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:49 047.png
-rwxrwxrwx 1 root root 5770 Feb 10 10:49 048.png
-rwxrwxrwx 1 root root 5741 Feb 10 10:50 049.png
-rwxrwxrwx 1 root root 5787 Feb 10 10:50 050.png
-rwxrwxrwx 1 root root 5767 Feb 10 10:50 051.png
-rwxrwxrwx 1 root root 5791 Feb 10 10:50 052.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:50 053.png
-rwxrwxrwx 1 root root 5789 Feb 10 10:50 054.png
-rwxrwxrwx 1 root root 5771 Feb 10 10:50 055.png
-rwxrwxrwx 1 root root 5792 Feb 10 10:51 056.png
-rwxrwxrwx 1 root root 5771 Feb 10 10:51 057.png
-rwxrwxrwx 1 root root 5787 Feb 10 10:51 058.png
-rwxrwxrwx 1 root root 5761 Feb 10 10:51 059.png
-rwxrwxrwx 1 root root 5790 Feb 10 10:51 060.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:51 061.png
-rwxrwxrwx 1 root root 5793 Feb 10 10:52 062.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:52 063.png
-rwxrwxrwx 1 root root 5786 Feb 10 10:52 064.png
-rwxrwxrwx 1 root root 5769 Feb 10 10:52 065.png
-rwxrwxrwx 1 root root 5793 Feb 10 10:52 066.png
-rwxrwxrwx 1 root root 5771 Feb 10 10:53 067.png
-rwxrwxrwx 1 root root 5778 Feb 10 10:53 068.png
-rwxrwxrwx 1 root root 5745 Feb 10 10:53 069.png
-rwxrwxrwx 1 root root 5789 Feb 10 10:53 070.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:53 071.png
-rwxrwxrwx 1 root root 5788 Feb 10 10:54 072.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:54 073.png
-rwxrwxrwx 1 root root 5786 Feb 10 10:54 074.png
-rwxrwxrwx 1 root root 5769 Feb 10 10:54 075.png
-rwxrwxrwx 1 root root 5789 Feb 10 10:55 076.png
-rwxrwxrwx 1 root root 5771 Feb 10 10:55 077.png
-rwxrwxrwx 1 root root 5781 Feb 10 10:55 078.png
-rwxrwxrwx 1 root root 5745 Feb 10 10:55 079.png
-rwxrwxrwx 1 root root 5787 Feb 10 10:55 080.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:56 081.png
-rwxrwxrwx 1 root root 5786 Feb 10 10:56 082.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:56 083.png
-rwxrwxrwx 1 root root 5782 Feb 10 10:56 084.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:57 085.png
-rwxrwxrwx 1 root root 5785 Feb 10 10:57 086.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:57 087.png
-rwxrwxrwx 1 root root 5770 Feb 10 10:58 088.png
-rwxrwxrwx 1 root root 5741 Feb 10 10:58 089.png
-rwxrwxrwx 1 root root 5787 Feb 10 10:58 090.png
-rwxrwxrwx 1 root root 5768 Feb 10 10:58 091.png
-rwxrwxrwx 1 root root 5791 Feb 10 10:59 092.png
-rwxrwxrwx 1 root root 5766 Feb 10 10:59 093.png
-rwxrwxrwx 1 root root 5785 Feb 10 10:59 094.png
-rwxrwxrwx 1 root root 5769 Feb 10 10:59 095.png
-rwxrwxrwx 1 root root 5792 Feb 10 11:00 096.png
-rwxrwxrwx 1 root root 5770 Feb 10 11:00 097.png
-rwxrwxrwx 1 root root 5783 Feb 10 11:00 098.png
-rwxrwxrwx 1 root root 5745 Feb 10 11:01 099.png
import imageio
images = []
filenames = ["/dbfs/keras_rl/images/{:03d}.png".format(x) for x in range(100)]
for filename in filenames:
images.append(imageio.imread(filename))
imageio.mimsave('/dbfs/FileStore/movie.gif', images)
dbutils.fs.cp("dbfs:///FileStore/movie.gif", "file:///databricks/driver/movie.gif")
ls
conf
derby.log
eventlogs
ganglia
logs
movie.gif

Where to Go Next?
The following articles are great next steps:
- Flappy Bird with DQL and Keras: https://yanpanlau.github.io/2016/07/10/FlappyBird-Keras.html
- DQL with Keras and an Open AI Gym task: http://koaning.io/hello-deepq.html
- Simple implementation with Open AI Gym support: https://github.com/sherjilozair/dqn
This project offers Keras add-on classes for simple experimentation with DQL:
- https://github.com/farizrahman4u/qlearning4k
- Note that you'll need to implement (or wrap) the "game" to plug into that framework
Try it at home:
- Hack the "Keras Plays Catch" demo to allow the ball to drift horizontally as it falls. Does it work?
- Try training the network on "delta frames" instead of static frames. This gives the network information about motion (implicitly).
- What if the screen is high-resolution? what happens? how could you handle it better?
And if you have the sneaking suspicion that there is a connection between PG and DQL, you'd be right: https://arxiv.org/abs/1704.06440
Check out latest databricks notebooks here:
- https://databricks.com/resources/type/example-notebook
CNNs
- https://pages.databricks.com/rs/094-YMS-629/images/Applying-Convolutional-Neural-Networks-with-TensorFlow.html
Distributed DL
- https://pages.databricks.com/rs/094-YMS-629/images/final%20-%20simple%20steps%20to%20distributed%20deep%20learning.html
- https://pages.databricks.com/rs/094-YMS-629/images/keras-hvdrunner-mlflow-mnist-experiments.html
And so much more!
ScaDaMaLe Course site and book
This is a 2019-2021 augmentation and update of Adam Breindel's initial notebooks.
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials Spark 3.0.1 and Python 3+ compliant.
Operations in the Real World
Practical Options, Tools, Patterns, and Considerations for Deep Learning
There are various ways to use deep learning in an enterprise setting that may not require designing your own networks!
Ways to Use Deep Learning
(in order from least complex/expensive investment to most)
[1] Load and use a pretrained model
Many of the existing toolkit projects offer models pretrained on datasets, including
- natural language corpus models
- image datasets like ImageNet (http://www.image-net.org/) or Google's Open Image Dataset (https://research.googleblog.com/2016/09/introducing-open-images-dataset.html)
- video datasets like the YouTube 8 million video dataset (https://research.googleblog.com/2016/09/announcing-youtube-8m-large-and-diverse.html)
[2] Augmenting a pretrained model with new training data, or using it in a related context (see Transfer Learning)
[3] Use a known, established network type (topology) but train on your own data
[4] Modify established network models for your specific problem
[5] Research and experiment with new types of models
Just because Google DeepMind, Facebook, and Microsoft are getting press for doing a lot of new research doesn't mean you have to do it too.


Data science and machine learning is challenging in general for enterprises (though some industries, such as pharma, have been doing it for a long time). Deep learning takes that even further, since deep learning experiments may require new kinds of hardware ... in some ways, it's more like chemistry than the average IT project!
Tools and Processes for your Deep Learning Pipeline
Data Munging
Most of the deep learning toolkits are focused on model-building performance or flexibility, less on production data processing.
However, Google recently introduced tf.Transform, a data processing pipeline project: https://github.com/tensorflow/transform
and Dataset, an API for data processing: https://www.tensorflow.org/api_docs/python/tf/contrib/data/Dataset
TensorFlow can read from HDFS and run on Hadoop although it does not scale out automatically on a Hadoop/Spark cluster: https://www.tensorflow.org/deploy/hadoop
Falling back to "regular" tools, we have Apache Spark for big data, and the Python family of pandas, sklearn, scipy, numpy.
Experimenting and Training
Once you want to scale beyond your laptop, there are few options...
- AWS GPU-enabled instances
- Deep-learning-infrastructure as a Service
- EASY
- "Floyd aims to be the Heroku of Deep Learning" https://www.floydhub.com/
- "Effortless infrastructure for deep learning" https://www.crestle.com/
- "GitHub of Machine Learning / We provide machine learning platform-as-a-service." https://valohai.com/
- "Machine Learning for Everyone" (may be in closed beta) https://machinelabs.ai
- Algorithms as a service / model deployment https://algorithmia.com/
- MEDIUM Google Cloud Platform "Cloud Machine Learning Engine" https://cloud.google.com/ml-engine/
- HARDER Amazon Deep Learning AMI + CloudFormation https://aws.amazon.com/blogs/compute/distributed-deep-learning-made-easy/
- EASY
- On your own infrastructure or VMs
- Distributed TensorFlow is free, OSS
- Apache Spark combined with Intel BigDL (CPU) or DeepLearning4J (GPU)
- TensorFlowOnSpark
- CERN Dist Keras (Spark + Keras) https://github.com/cerndb/dist-keras
Frameworks
We've focused on TensorFlow and Keras, because that's where the "center of mass" is at the moment.
But there are lots of others. Major ones include:
- Caffe
- PaddlePaddle
- Theano
- CNTK
- MXNet
- DeepLearning4J
- BigDL
- Torch/PyTorch
- NVIDIA Digits
and there are at least a dozen more minor ones.
Taking Your Trained Model to Production
Most trained models can predict in production in near-zero time. (Recall the forward pass is just a bunch of multiplication and addition with a few other calculations thrown in.)
For a neat example, you can persist Keras models and load them to run live in a browser with Keras.js
See Keras.js for code and demos: https://github.com/transcranial/keras-js

TensorFlow has an Android example at https://github.com/tensorflow/tensorflow/tree/master/tensorflow/examples/android
and Apple CoreML supports Keras models: https://developer.apple.com/documentation/coreml/convertingtrainedmodelstocore_ml
(remember, the model is already trained, we're just predicting here)
And for your server-side model update-and-serve tasks, or bulk prediction at scale...
(imagine classifying huge batches of images, or analyzing millions of chat messages or emails)
-
TensorFlow has a project called TensorFlow Serving: https://tensorflow.github.io/serving/
-
Spark Deep Learning Pipelines (bulk/SQL inference) https://github.com/databricks/spark-deep-learning
-
Apache Spark + (DL4J | BigDL | TensorFlowOnSpark)
-
DeepLearning4J can import your Keras model: https://deeplearning4j.org/model-import-keras
- (which is a really nice contribution, but not magic -- remember the model is just a pile of weights, convolution kernels, etc. ... in the worst case, many thousands of floats)
-
http://pipeline.io/ by Netflix and Databricks alum Chris Fregly
-
MLeap http://mleap-docs.combust.ml/
Security and Robustness
A recent (3/2017) paper on general key failure modes is Failures of Deep Learning: https://arxiv.org/abs/1703.07950
Deep learning models are subject to a variety of unexpected perturbations and adversarial data -- even when they seem to "understand," they definitely don't understand in a way that is similar to us.

Ian Goodfellow has distilled and referenced some of the research here: https://openai.com/blog/adversarial-example-research/
- He is also maintainer of an open-source project to measure robustness to adversarial examples, Clever Hans: https://github.com/tensorflow/cleverhans
- Another good project in that space is Foolbox: https://github.com/bethgelab/foolbox
It's all fun and games until a few tiny stickers that a human won't even notice ... turn a stop sign into a "go" sign for your self-driving car ... and that's exactly what this team of researchers has done in Robust Physical-World Attacks on Machine Learning Models: https://arxiv.org/pdf/1707.08945v1.pdf
Final Notes
The research and projects are coming so fast that this will probably be outdated by the time you see it ...
2017 is the last ILSVRC! http://image-net.org/challenges/beyond_ilsvrc.php
Try visualizing principal components of high-dimensional data with TensorFlow Embedding Projector http://projector.tensorflow.org/
Or explore with Google / PAIR's Facets tool: https://pair-code.github.io/facets/
Visualize the behavior of Keras models with keras-vis: https://raghakot.github.io/keras-vis/
Want more out of Keras without coding it yourself? See if your needs are covered in the extension repo for keras, keras-contrib: https://github.com/farizrahman4u/keras-contrib
Interested in a slightly different approach to APIs, featuring interactive (imperative) execution? In the past year, a lot of people have started using PyTorch: http://pytorch.org/
XLA, an experimental compiler to make TensorFlow even faster: https://www.tensorflow.org/versions/master/experimental/xla/
...and in addition to refinements of what we've already talked about, there is bleeding-edge work in
- Neural Turing Machines
- Code-generating Networks
- Network-designing Networks
- Evolution Strategies (ES) as an alternative to DQL / PG: https://arxiv.org/abs/1703.03864
Books
To fill in gaps, refresh your memory, gain deeper intuition and understanding, and explore theoretical underpinnings of deep learning...
Easier intro books (less math)
Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurélien Géron
Deep Learning with Python by Francois Chollet
Fundamentals of Machine Learning for Predictive Data Analytics: Algorithms, Worked Examples, and Case Studies by John D. Kelleher, Brian Mac Namee, Aoife D'Arcy
More thorough books (more math)
Deep Learning by Ian Goodfellow, Yoshua Bengio, Aaron Courville
Information Theory, Inference and Learning Algorithms 1st Edition by David J. C. MacKay
Tutorial MLOps
This is a redefined notebook made available on a webinar hosted by Databricks, going through the whole pipeline of MLOps using delta lakes and model serving. You can watch the webinar here (approx. 1h40m - this notebook demo starts after approx. 30 minutes).
Thanks to Christian von Koch and William Anzén for their contributions towards making these materials work on this particular Databricks Shard.
Note: The steps for uploading data on the Databricks Shard can be found in the end of this notebook. The steps below starts from a point where the data is already uploaded to the Databricks Shard.
From X-rays to a Production Classifier with MLflow
This simple example will demonstrate how to build a chest X-Ray classifer with PyTorch Lightning, and explain its output, but more importantly, will demonstrate how to manage the model's deployment to production as a REST service with MLflow and its Model Registry.

The National Institute of Health (NIH) released a dataset of 45,000 chest X-rays of patients who may suffer from some problem in the chest cavity, along with several of 14 possible diagnoses. This was accompanied by a paper analyzing the data set and presenting a classification model.
The task here is to train a classifier that learns to predict these diagnoses. Note that each image may have 0 or several 'labels'. This data set was the subject of a Kaggle competition as well.
Data Engineering
The image data is provided as a series of compressed archives. However they are also available from Kaggle with other useful information, like labels and bounding boxes. In this problem, only the images will be used, unpacked into an .../images/ directory,, and the CSV file of label information Data_Entry_2017.csv at a .../metadata/ path.
The images can be read directly and browsed with Apache Spark:
raw_image_df = spark.read.format("image").load("dbfs:/datasets/ScaDaMaLe/nih-chest-xrays/images/raw/") # This is the path where the xray images has been uploaded into dbfs.
display(raw_image_df)
Managing Unstructured Data with Delta Lake
Although the images can be read directly as files, it will be useful to manage the data as a Delta table:
- Delta provides transactional updates, so that the data set can be updated, and still read safely while being updated
- Delta provides "time travel" to view previous states of the data set
- Reading batches of image data is more efficient from Delta than from many small files
- The image data needs some one-time preprocessing beforehand anyway
In this case, the images are all 1024 x 1024 grayscale images, though some arrive as 4-channel RGBA. They are normalized to 224 x 224 single-channel image data:
from pyspark.sql.types import BinaryType, StringType
from PIL import Image
import numpy as np
def to_grayscale(data, channels):
np_array = np.array(data, dtype=np.uint8)
if channels == 1: # assume mode = 0
grayscale = np_array.reshape((1024,1024))
else: # channels == 4 and mode == 24
reshaped = np_array.reshape((1024,1024,4))
# Data is BGRA; ignore alpha and use ITU BT.709 luma conversion:
grayscale = (0.0722 * reshaped[:,:,0] + 0.7152 * reshaped[:,:,1] + 0.2126 * reshaped[:,:,2]).astype(np.uint8)
# Use PIL to resize to match DL model that it will feed
resized = Image.frombytes('L', (1024,1024), grayscale).resize((224,224), resample=Image.LANCZOS)
return np.asarray(resized, dtype=np.uint8).flatten().tobytes()
to_grayscale_udf = udf(to_grayscale, BinaryType())
to_filename_udf = udf(lambda f: f.split("/")[-1], StringType())
image_df = raw_image_df.select(
to_filename_udf("image.origin").alias("origin"),
to_grayscale_udf("image.data", "image.nChannels").alias("image"))
The file of metadata links the image file name to its labels. These are parsed and joined, written to a Delta table, and registered in the metastore:
raw_metadata_df = spark.read.\
option("header", True).option("inferSchema", True).\
csv("dbfs:/datasets/ScaDaMaLe/nih-chest-xrays/metadata/").\
select("Image Index", "Finding Labels")
display(raw_metadata_df)
from pyspark.sql.functions import explode, split
from pyspark.sql.types import BooleanType, StructType, StructField
distinct_findings = sorted([r["col"] for r in raw_metadata_df.select(explode(split("Finding Labels", r"\|"))).distinct().collect() if r["col"] != "No Finding"])
encode_findings_schema = StructType([StructField(f.replace(" ", "_"), BooleanType(), False) for f in distinct_findings])
def encode_finding(raw_findings):
findings = raw_findings.split("|")
return [f in findings for f in distinct_findings]
encode_finding_udf = udf(encode_finding, encode_findings_schema)
metadata_df = raw_metadata_df.withColumn("encoded_findings", encode_finding_udf("Finding Labels")).select("Image Index", "encoded_findings.*")
table_path = "/tmp/nih-chest-xrays/image_table/"
metadata_df.join(image_df, metadata_df["Image Index"] == image_df["origin"]).drop("Image Index", "origin").write.mode("overwrite").format("delta").save(table_path)
CREATE DATABASE IF NOT EXISTS nih_xray;
USE nih_xray;
CREATE TABLE IF NOT EXISTS images USING DELTA LOCATION '/tmp/nih-chest-xrays/image_table/';
Now we optimize the newly created table so that fetching data is more efficient.
OPTIMIZE images;
Modeling with PyTorch Lightning and MLflow
PyTorch is of course one of the most popular tools for building deep learning models, and is well suited to build a convolutional neural net that works well as a multi-label classifier for these images. Below, other related tools like torchvision and PyTorch Lightning are used to simplify expressing and building the classifier.
The data set isn't that large once preprocessed - about 2.2GB. For simplicity, the data will be loaded and manipulated with pandas from the Delta table, and model trained on one GPU. It's also quite possible to scale to multiple GPUs, or scale across machines with Spark and Horovod, but it won't be necessary to add that complexity in this example.
from sklearn.model_selection import train_test_split
df = spark.read.table("nih_xray.images")
display(df)
train_pd, test_pd = train_test_split(df.toPandas(), test_size=0.1, random_state=42) # Need to increase spark.driver.maxResultSize to at least 8GB through pasting spark.driver.maxResultSize <X>g in cluster Spark config
frac_positive = train_pd.drop("image", axis=1).sum().sum() / train_pd.drop("image", axis=1).size
disease_names = df.drop("image").columns
num_classes = len(disease_names)
torchvision provides utilities that make it simple to perform some model-specific transformation as part of the model. Here, a pre-trained network will be used which requires normalized 3-channel RGB data as PyTorch Tensors:
from torchvision import transforms
transforms = transforms.Compose([
transforms.ToPILImage(),
transforms.Lambda(lambda image: image.convert('RGB')),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
])
Define the Dataset and train/test DataLoaders for this data set in PyTorch:
from torch.utils.data import Dataset, DataLoader
import numpy as np
class XRayDataset(Dataset):
def __init__(self, data_pd, transforms):
self.data_pd = data_pd
self.transforms = transforms
def __len__(self):
return len(self.data_pd)
def __getitem__(self, idx):
image = np.frombuffer(self.data_pd["image"].iloc[idx], dtype=np.uint8).reshape((224,224))
labels = self.data_pd.drop("image", axis=1).iloc[idx].values.astype(np.float32)
return self.transforms(image), labels
train_loader = DataLoader(XRayDataset(train_pd, transforms), batch_size=64, num_workers=8, shuffle=True)
test_loader = DataLoader(XRayDataset(test_pd, transforms), batch_size=64, num_workers=8)
Note that MLflow natively supports logging PyTorch models of course, but, can also automatically log the output of models defined with PyTorch Lightning:
import mlflow.pytorch
mlflow.pytorch.autolog()
Finally, the model is defined, and fit. For simple purposes here, the model itself is quite simple: it employs the pretrained densenet121 layers to do most of the work (layers which are not further trained here), and simply adds some dropout and a dense layer on top to perform the classification. No attempt is made here to tune the network's architecture or parameters further.
For those new to PyTorch Lightning, it is still "PyTorch", but removes the need to write much of PyTorch's boilerplate code. Instead, a LightningModule class is implemented with key portions like model definition and fitting processes defined.
Note: This section should be run on a GPU. An NVIDIA T4 GPU is recommended, though any modern GPU should work. This code can also be easily changed to train on CPUs or TPUs.
import torch
from torch.optim import Adam
from torch.nn import Dropout, Linear
from torch.nn.functional import binary_cross_entropy_with_logits
from sklearn.metrics import log_loss
import pytorch_lightning as pl
from pytorch_lightning.callbacks.early_stopping import EarlyStopping
class XRayNNLightning(pl.LightningModule):
def __init__(self, learning_rate, pos_weights):
super(XRayNNLightning, self).__init__()
self.densenet = torch.hub.load('pytorch/vision:v0.6.0', 'densenet121', pretrained=True)
for param in self.densenet.parameters():
param.requires_grad = False
self.dropout = Dropout(0.5)
self.linear = Linear(1000, num_classes)
# No sigmoid here; output logits
self.learning_rate = learning_rate
self.pos_weights = pos_weights
def get_densenet():
return self.densenet
def forward(self, x):
x = self.densenet(x)
x = self.dropout(x)
x = self.linear(x)
return x
def configure_optimizers(self):
return Adam(self.parameters(), lr=self.learning_rate)
def training_step(self, train_batch, batch_idx):
x, y = train_batch
output = self.forward(x)
# Outputting logits above lets us use binary_cross_entropy_with_logits for efficiency, but also, allows the use of
# pos_weight to express that positive labels should be given much more weight.
# Note this was also proposed in the paper linked above.
loss = binary_cross_entropy_with_logits(output, y, pos_weight=torch.tensor(self.pos_weights).to(self.device))
self.log('train_loss', loss)
return loss
def validation_step(self, val_batch, batch_idx):
x, y = val_batch
output = self.forward(x)
val_loss = binary_cross_entropy_with_logits(output, y, pos_weight=torch.tensor(self.pos_weights).to(self.device))
self.log('val_loss', val_loss)
model = XRayNNLightning(learning_rate=0.001, pos_weights=[[1.0 / frac_positive] * num_classes])
# Let PyTorch handle learning rate, batch size tuning, as well as early stopping.
# Change here to configure for CPUs or TPUs.
trainer = pl.Trainer(gpus=1, max_epochs=20,
auto_scale_batch_size='binsearch',
auto_lr_find=True,
callbacks=[EarlyStopping(monitor='val_loss', patience=3, verbose=True)])
trainer.fit(model, train_loader, test_loader)
# As of version MLFlow 1.13.1, the framework seems to have trouble saving the pytorch lightning module through mlflow.pytorch.autolog() even though it should according to the documentation.
There seems to be a bug with MLFlow, not able to autolog model from Pytorch. Instead we save the trained model at a custom path instead, enabling us to load it in later stage.
path_to_model = "/dbfs/tmp/xray"
import os.path, shutil
from os import path
if path.exists(path_to_model):
print("A model already exists in this path. It will be overwritten...")
shutil.rmtree(path_to_model)
mlflow.pytorch.save_model(model, path_to_model)
else:
mlflow.pytorch.save_model(model, path_to_model)
Although not shown here for brevity, this model's results are comparable to those cited in the paper - about 0.6-0.7 AUC for each of the 14 classes. The auto-logged results are available in MLflow:


PSA: Don't Try (To Diagnose Chest X-rays) At Home!
The author is not a doctor, and probably neither are you! It should be said that this is not necessarily the best model, and certainly should not be used to actually diagnose patients! It's just an example.
Serving the Model with MLflow
This auto-logged model is useful raw material. The goal is to deploy it as a REST API, and MLflow can create a REST API and Docker container around a pyfunc model, and even deploy to Azure ML or AWS SageMaker for you. It can also be deployed within Databricks for testing.
However, there are a few catches which mean we can't directly deploy the model above:
- It accepts images as input, but these can't be directly specified in the JSON request to the REST API
- Its output are logits, when probabilities (and label names) would be more useful
It is however easy to define a custom PythonModel that will wrap the PyTorch model and perform additional pre- and post-processing. This model accepts a base64-encoded image file, and returns the probability each label:
import torch
import pandas as pd
import numpy as np
import base64
from io import BytesIO
from PIL import Image
from mlflow.pyfunc import PythonModel
class XRayNNServingModel(PythonModel):
def __init__(self, model, transforms, disease_names):
self.model = model
self.transforms = transforms
self.disease_names = disease_names
def get_model():
return self.model
def get_transforms():
return self.transforms
def get_disease_names():
return disease_names
def predict(self, context, model_input):
def infer(b64_string):
encoded_image = base64.decodebytes(bytearray(b64_string, encoding="utf8"))
image = Image.open(BytesIO(encoded_image)).convert(mode='L').resize((224,224), resample=Image.LANCZOS)
image_bytes = np.asarray(image, dtype=np.uint8)
transformed = self.transforms(image_bytes).unsqueeze(dim=0)
output = self.model(transformed).squeeze()
return torch.sigmoid(output).tolist()
return pd.DataFrame(model_input.iloc[:,0].apply(infer).to_list(), columns=disease_names)
Now the new wrapped model is logged with MLflow:
import mlflow.pyfunc
import mlflow.pytorch
import mlflow.models
import pytorch_lightning as pl
import PIL
import torchvision
# Load PyTorch Lightning model
# Loading the model previously saved
loaded_model = mlflow.pytorch.load_model(path_to_model, map_location='cpu')
with mlflow.start_run():
model_env = mlflow.pyfunc.get_default_conda_env()
# Record specific additional dependencies required by the serving model
model_env['dependencies'][-1]['pip'] += [
f'torch=={torch.__version__}',
f'torchvision=={torchvision.__version__}',
f'pytorch-lightning=={pl.__version__}',
f'pillow=={PIL.__version__}',
]
# Log the model signature - just creates some dummy data of the right type to infer from
signature = mlflow.models.infer_signature(
pd.DataFrame(["dummy"], columns=["image"]),
pd.DataFrame([[0.0] * num_classes], columns=disease_names))
python_model = XRayNNServingModel(loaded_model, transforms, disease_names)
mlflow.pyfunc.log_model("model", python_model=python_model, signature=signature, conda_env=model_env) # This autolog worked. Seems to be an issue with autologging pytorch-lightning models...
Registering the Model with MLflow
The MLflow Model Registry provides workflow management for the model promotion process, from Staging to Production. The new run created above can be registered directly from the MLflow UI:

It can then be transitioned into the Production state directly, for simple purposes here. After that, enabling serving within Databricks is as simple as turning it on in the models' Serving tab:

Accessing the Model with a REST Request
Now, we can send images to the REST endpoint and observe its classifications. This could power a simple web application, but here, to demonstrate, it is called directly from a notebook.
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
image_path = "/dbfs/datasets/ScaDaMaLe/nih-chest-xrays/images/raw/00000001_000.png"
plt.imshow(mpimg.imread(image_path), cmap='gray')
Note: In the next cell you need to use your Databricks token for accessing Databricks from the internet. It is best practice to use the Databricks Secrets CLI to avoid putting secret keys in notebooks. Please refer to this guide for setting it up through the Databricks CLI.
import base64
import requests
import pandas as pd
with open(image_path, "rb") as file:
content = file.read()
dataset = pd.DataFrame([base64.encodebytes(content)], columns=["image"])
# Note that you will still need a Databricks access token to send with the request. This can/should be stored as a secret in the workspace:
token = dbutils.secrets.get("databricksEducational", "databricksCLIToken") # These are just examples of a Secret Scope and Secret Key. Please refer to guide in above cell...
response = requests.request(method='POST',
headers={'Authorization': f'Bearer {token}'},
url='https://dbc-635ca498-e5f1.cloud.databricks.com/model/nih_xray/1/invocations',
json=dataset.to_dict(orient='split'))
pd.DataFrame(response.json())
The model suggests that a doctor might examine this X-ray for Atelectasis and Infiltration, but a Hernia is unlikely, for example. But, why did the model think so? Fortunately there are tools that can explain the model's output in this case, and this will be demonstrated a little later.
Adding Webhooks for Model State Management
MLflow can now trigger webhooks when Model Registry events happen. Webhooks are standard 'callbacks' which let applications signal one another. For example, a webhook can cause a CI/CD test job to start and run tests on a model. In this simple example, we'll just set up a webhook that posts a message to a Slack channel.
Note: the example below requires a registered Slack webhook. Because the webhook URL is sensitive, it is stored as a secret in the workspace and not included inline.
The Slack Webhook part of the tutorial has not been tested. Feel free to try to set it up.
from mlflow.tracking.client import MlflowClient
from mlflow.utils.rest_utils import http_request
import json
def mlflow_call_endpoint(endpoint, method, body = '{}'):
client = MlflowClient()
host_creds = client._tracking_client.store.get_host_creds()
if method == 'GET':
response = http_request(host_creds=host_creds, endpoint=f"/api/2.0/mlflow/{endpoint}", method=method, params=json.loads(body))
else:
response = http_request(host_creds=host_creds, endpoint=f"/api/2.0/mlflow/{endpoint}", method=method, json=json.loads(body))
return response.json()
json_obj = {
"model_name": "nih_xray",
"events": ["MODEL_VERSION_CREATED", "TRANSITION_REQUEST_CREATED", "MODEL_VERSION_TRANSITIONED_STAGE", "COMMENT_CREATED", "MODEL_VERSION_TAG_SET"],
"http_url_spec": { "url": dbutils.secrets.get("demo-token-sean.owen", "slack_webhook") }
}
mlflow_call_endpoint("registry-webhooks/create", "POST", body=json.dumps(json_obj))
As model versions are added, transitioned among stages, commented on, etc. a webhook will fire.

Explaining Predictions
SHAP is a popular tool for explaining model predictions. It can explain virtually any classifier or regressor at the prediction level, and estimate how much each input feature contributed positively or negatively to the result, and by how much.
In MLflow 1.12 and later, SHAP model explanations can be logged automatically:

However, this model's inputs are not simple scalar features, but an image. SHAP does have tools like GradExplainer and DeepExplainer that are specifically designed to explain neural nets' classification of images. To use this, we do have to use SHAP manually instead of via MLflow's automated tools. However the result can be, for example, logged with a model in MLflow.
Here we explain the model's top classification, and generate a plot showing which parts of the image most strongly move the prediction positively (red) or negatively (blue). The explanation is traced back to an early intermediate layer of densenet121.
import numpy as np
import torch
import mlflow.pyfunc
import shap
# Load the latest production model and its components
pyfunc_model = mlflow.pyfunc.load_model("models:/nih_xray/production")
transforms = pyfunc_model._model_impl.python_model.transforms
model = pyfunc_model._model_impl.python_model.model
disease_names = pyfunc_model._model_impl.python_model.disease_names
# Let's pick an example that definitely exhibits some affliction
df = spark.read.table("nih_xray.images")
first_row = df.filter("Infiltration").select("image").limit(1).toPandas()
image = np.frombuffer(first_row["image"].item(), dtype=np.uint8).reshape((224,224))
# Only need a small sample for explanations
sample = df.sample(0.02).select("image").toPandas()
sample_tensor = torch.cat([transforms(np.frombuffer(sample["image"].iloc[idx], dtype=np.uint8).reshape((224,224))).unsqueeze(dim=0) for idx in range(len(sample))])
e = shap.GradientExplainer((model, model.densenet.features[6]), sample_tensor, local_smoothing=0.1)
shap_values, indexes = e.shap_values(transforms(image).unsqueeze(dim=0), ranked_outputs=3, nsamples=300)
shap.image_plot(shap_values[0][0].mean(axis=0, keepdims=True),
transforms(image).numpy().mean(axis=0, keepdims=True))
import pandas as pd
pd.DataFrame(torch.sigmoid(model(transforms(image).unsqueeze(dim=0))).detach().numpy(), columns=disease_names).iloc[:,indexes.numpy()[0]]
This suggests that the small region at the top of left lung is more significant in causing the model to produce its positive classifications for Infiltration, Effusion and Cardiomegaly than most of the image, and the bottom of the left lung however contradicts those to some degree and is associated with lower probability of that classification.
Managing Notebooks with Projects
This notebook exists within a Project. This means it and any related notebooks are backed by a Git repository. The notebook can be committed, along with other notebooks, and observed in the source Git repository.

Uploading Data to Databricks Shard (Mac)
Step 1: Download Homebrew - follow the instructions on the link.
Step 2: Download python with brew in order to get pip on your computer. Follow this guide here for installing Python and adding it to your PATH.
Step 3: Install Databricks CLI
Run the following command in your terminal to install the Databricks Command Line Interface:
pip install databricks-cli
Step 4: Press your user symbol in the upper right of this page and press User Settings. Press Access Tokens and generate a new token with an appropriate name and appropriate lifetime. This is for connecting your local comuter to this specific Databricks shard.
Step 5: Follow the instructions for configuring your Databricks CLI with your generated token here.
Step 6: Download the data from Kaggle Chest X-rays.
Step 7: Run the command below in your local terminal. Note: You might need to run multiple commands since the Kaggle images lies in different folders after download. In this case, separate each command with a ;.
dbfs cp -r <Path to the folder with the Kaggle images> dbfs:/datasets/<Desired Path to the images on Databricks>; dbfs cp -r <Path to another folder with the Kaggle images> dbfs:/datasets/<Desired Path to the images on Databricks>
Step 8: After the commands have successfully completed, the images should lie within the Databricks shard in the following path:
/dbfs/datasets/<Desired Path to the images on Databricks>
You can verify this by running the following command in any notebook on the Databricks shard which you uploaded the images into:
%sh ls /dbfs/datasets/


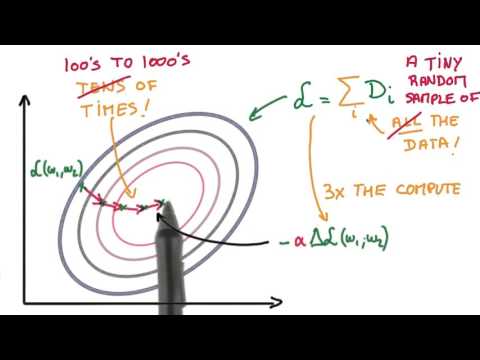
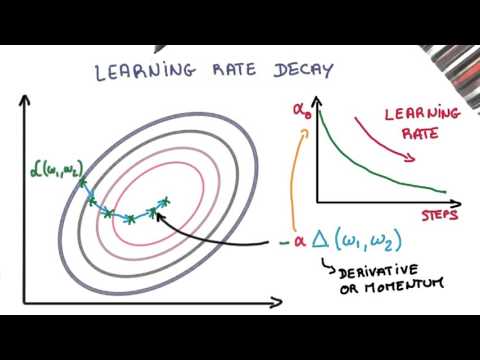



 *** Watch now (3:51)
*** Watch now (3:51)